技術文章 » 強化學習-學習筆記2 | 價值學習

強化學習-學習筆記2 | 價值學習

2022-07-04 21:00:57

Value-Based Reinforcement Learning : 價值學習

2. 價值學習

2.1 Deep Q-Network DQN

其實就是用一個神經網路來近似 \(Q*\) 函數。

agent 的目標是打贏遊戲，如果用強化學習的語言來講，就是在遊戲結束的時候拿到的獎勵總和 Rewards 越大越好。

a. Q-star Function

問題：假設知道了 \(Q^*(s,a)\) 函數，哪個是最好的動作？

顯然，最好的動作是\(a^* = \mathop{argmax}\limits_{a}Q^*(s,a)\) ，

\(Q^*(s,a)\)可以給每個動作打分，就像一個先知，能告訴你每個動作帶來的平均回報，選平均回報最高的那個動作。

但事實是，每個人都無法預測未來，我們並不知道\(Q^*(s,a)\)。而價值學習就在於學習出一個函數來近似\(Q^*(s,a)\) 作決策。

  • 解決：Deep Q-network(DQN)，即用一個神經網路 \(Q(s,a;w)\)來近似 \(Q^*(s,a)\) 函數。
  • 神經網路引數是 w ，輸入是狀態 s，輸出是對所有可能動作的打分，每一個動作對應一個分數。
  • 通過獎勵來學習這個神經網路，這個網路給動作的打分就會逐漸改進，越來越精準
  • 玩上幾百萬次超級瑪麗，就能訓練出一個先知。

b. Example

對於不同的案例，DQN 的結構會不一樣。

如果是玩超級瑪麗

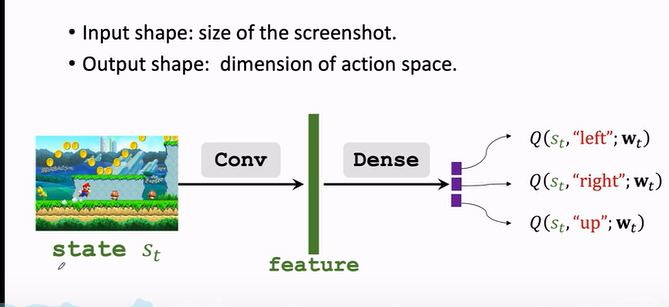
  • 螢幕畫面作為輸入
  • 用一個折積層把圖片變成特徵向量
  • 最後用幾個全連線層把特徵對映到一個輸出的向量
  • 輸出的向量就是對動作的打分，向量每一個元素對應一個動作的分值，agent 會選擇分值最大的方向進行動作。

c. 用 DQN 打遊戲

DQN 的具體執行過程如下：

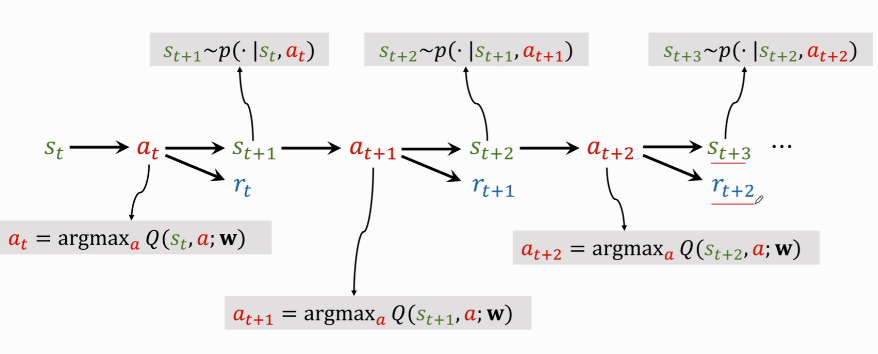
分步解釋：

  • $ s_t \rightarrow a_t$：當前觀測到狀態 \(s_t\)，用公式 $ a_t=\mathop{argmax}\limits_{a}Q^*(s,a)$ 把 \(s_t\) 作為輸入，給所有動作打分，選出分數最高的動作 \(a_t\) 。
  • agent 執行 \(a_t\) 這個動作後，環境會改變狀態，用狀態轉移函數 \(p(\cdot|s_t,a_t)\) 隨機抽樣得出一個新狀態 \(s_{t+1}\)。
  • 環境還會告訴這一步的獎勵 \(r_t\) ，獎勵就是強化學習中的監督訊號，DQN靠這些獎勵來訓練。
  • 有了新的狀態 \(s_{t+1}\)，DQN 繼續對所有動作打分，agent 選擇分數最高動作 \(a_{t+1}\)。
  • 執行 \(a_{t+1}\) 後，環境會再更新一個狀態 \(s_{t+2}\)，給出一個獎勵 \(r_{t+1}\)。
  • 然後不斷迴圈往復，直到遊戲結束

2.2 TD 學習

如何訓練 DQN ？最常使用的是 Temporal Difference Learning。TD學習的原理可以用下面這個例子來展示：

a. 案例分析

要開車從紐約到亞特蘭大，有一個模型\(Q(w)\)預測出開車出行的開銷是1000分鐘。這個預測可能不準，需要更多的人提供資料來訓練模型使得預測更準。

  1. 問題：需要怎樣的資料？如何更新模型。

  • 出發之前讓模型做一個預測，記作\(q\)，\(q=Q(w)\)，比如\(q=1000\)。到了目的地，發現其實只用了860分鐘，獲取真實值 \(y=860\)。

  • 實際值\(y\)與預測值\(q\)有偏差，這就造成了 loss 損失

  • loss 定義為實際值與預測值的平方差：\(L=\frac{1}{2}(q-y)^2\)

  • 對損失 \(L\)關於引數\(w\)求導並用鏈式法則展開：

    \(\frac{\partial L}{\partial w} = \frac{\partial q}{\partial w} \cdot \frac{\partial L}{\partial q} =(q-y)\cdot\frac{\partial Q(w)}{\partial w}\)

  • 梯度求出來了，可以用梯度下降來更新模型引數 w ：\(w_{t+1} = w_t - \alpha \cdot \frac{\partial L}{\partial w} \vert _{w=w_t}\)

缺點：這種演演算法比較 naive，因為要完成整個旅程才能完成對模型做一次更新。

那麼問題來了：假如不完成整個旅行，能否完成對模型的更新？

可以用 TD 的思想來考慮這件事情。比如我們中途路過 DC 不走了，沒去亞特蘭大，可以用 TD 演演算法完成對模型的更新，即

  • 出發前預測：NYC -> Atlanta 要花1000分鐘，這是預測值。

    到了 DC 時，發現用了 300 分鐘，這是真實觀測值，儘管它是針對於部分的。

  • 模型這時候又告知，DC -> Atlanta 要花 600 分鐘。

  • 模型原本預測：$Q(w) = 1000 $，而到 DC 的新預測：300 + 600 = 900，這個新的 900 估值就叫 TD target 。

    這些名詞要記住，後面會反覆使用，TD target 是使用了 TD演演算法的道德整體預測值。

  • TD target \(y=900\)雖然也是個估計預測值，但是比最初的 1000 分鐘更可靠，因為有事實成分。

  • 把 TD target \(y\) 就當作真實值：\(L = \frac{1}{2}(Q(w)-y)^2\), 其中$Q(w) - y $稱為TD error。

  • 求導：\(\frac{\partial L}{\partial w} =(1000-900)\cdot\frac{\partial Q(w)}{\partial w}\)

  • 梯度下降更新模型引數 w ：\(w_{t+1} = w_t - \alpha \cdot \frac{\partial L}{\partial w} \vert _{w=w_t}\)

b. 演演算法原理

換個角度來想，TD 的過程就是這樣子的：

模型預測 NYC -> Atlanta = 1000, DC -> Atlanta = 600，兩者差為400，也就是NYC -> DC = 400，但實際只花了300分鐘預計時間與真實時間之間的差就是TD error：\(\delta = 400-300 = 100\)。

TD 演演算法目標在於讓 TD error 儘量接近 0 。

即我們用部分的真實 修改 部分的預測，而使得整體的預測更加接近真實。我們可以通過反覆校準 可知的這部分真實 來接近我們的理想情況。

c. 用於 DQN

(1) 公式引入

上述例子中有這樣一個公式：$T_{NYC\rightarrow ATL} \approx T_{NYC\rightarrow DC} + T_{DC\rightarrow ATL} $

想要用 TD 演演算法，就必須要用類似這樣的公式，等式左邊有一項，右邊有兩項，其中有一項是真實觀測到的。

而在此之前，在深度強化學習中也有一個這樣的公式：\(Q(s_t,a_t;w)=r_t+\gamma \cdot Q(s_{t+1},a_{t+1};w)\)。

公式解釋：

  1. 左邊是 DQN 在 t 時刻做的估計，這是未來獎勵總和的期望，相當於 NYC 到 ATL 的預估總時間。
  2. 右邊 \(r_t\)是真實觀測到的獎勵，相當於 NYC 到 DC 。
  3. \(Q(s_{t+1},a_{t+1};w)\) 是 DQN 在 t+1 時刻做的估計，相當於 DC 到 ATL 的預估時間。
(2) 公式推導

為什麼會有一個這樣的公式？

回顧 Discounted return: \(U_t=R_t+\gamma R_{t+1}+\gamma^2 R_{t+2}+\gamma^3 R_{t+3}+\cdots\)

提出 \(\gamma\) 就得到 $ = R_t + \gamma(R_{t+1}+ \gamma R_{t+2}+ \gamma^2 R_{t+3}+\cdots) $

後面這些項就可以寫成\(U_{t+1}\),即 \(=R_t+\gamma U_{t+1}\)

這樣就得到：\(U_t = R_t + \gamma \cdot U_{t+1}\)

直觀上講，這就是相鄰兩個折扣演演算法的數學關係。

(3) 應用過程

現在要把 TD 演演算法用到 DQN 上

  • t 時刻 DQN 輸出的值 \(Q(s_t,a_t; w)\) 是對 \(U_t\) 作出的估計 \(\mathbb{E}[U_t]\)，類似於 NYC 到 ATL 的預估總時間。
  • 下一時刻 DQN 輸出的值 \(Q(s_{t+1},a_{t+1}; w)\) 是對 \(U_{t+1}\) 作出的估計 \(\mathbb{E}[U_{t+1}]\)，類似於 DC 到 ATL 的第二段預估時間。
  • 由於 \(U_t = R_t + \gamma \cdot U_{t+1}\)
  • 所以 \(\underbrace{Q(s_t,a_t; w) }_{\approx\mathbb{E}[U_t]}\approx \mathbb{E}[R_t+\gamma \cdot \underbrace{Q(s_{t+1},a_{t+1}; w)}_{\approx\mathbb{E}[U_{t+1}]}]\)
  • \(\underbrace{Q(s_t,a_t;w)}_{prediction}=\underbrace{r_t+\gamma \cdot Q(s_{t+1},a_{t+1};w)}_{TD\ \ target}\)

有了 prediction 和 TD target ，就可以更新 DQN 的模型引數了。

  • t 時刻模型做出預測 \(Q(s_t,a_t;w_t)\)；

  • 到了 t+1時刻，觀測到了真實獎勵 \(r_t\) 以及新的狀態 \(s_{t+1}\)，然後算出新的動作 \(a_{t+1}\)。

  • 這時候可以計算 TD target 記作 \(y_t\)，其中\(y_t=r_t+\gamma \cdot Q(s_{t+1},a_{t+1};w）\)

  • t+1 時刻的動作 \(a_{t+1}\)怎麼算的？DQN 要對每個動作打分，取分最高的，所以等於Q 函數關於a求最大化：$ y_t = r_t + \gamma \cdot \mathop{max}\limits_{a} Q(s_{t+1},a;w_t）$

  • 我們希望預測\(Q(s_{t},a_{t};w)\)儘可能接近 TD target \(y_t\) ，所以我們把兩者之差作為 Loss :

    \(L_t=\frac{1}{2}[Q(s_{t},a_{t};w)-y_t]^2\)

  • 做梯度下降：\(w_{t+1} = w_t - \alpha \cdot \frac{\partial L}{\partial w} \vert _{w=w_t}\)更新模型引數 w，來讓 Loss 更小

2.3 總結

  1. 價值學習（本講是DQN）基於最優動作價值函數 Q-star ：

    \(Q^*(s_t,a_t) = \mathbb{E}[U_t|S_t=s_t,A_t=a_t]\)

    對 \(U_t\) 求期望，能對每個動作打分，反映每個動作好壞程度，用這個函數來控制agent。

  2. DQN 就是用一個神經網路\(Q(s,a;w)\)來近似$Q^*(s,a) $

    1. 神經網路引數是 w ，輸入是 agent 的狀態 s
    2. 輸出是對所有可能動作 $ a \in A$ 的打分

  3. TD 演演算法過程

    1. 觀測當前狀態 $S_t = s_t $ 和已經執行的動作 \(A_t = a_t\)

    2. 用 DQN 做一次計算，輸入是狀態 \(s_t\)，輸出是對動作 \(a_t\) 的打分

      記作\(q_t\)，\(q_t = Q(s_t,a_t;w)\)

    3. 反向傳播對 DQN 求導：\(d_t = \frac{\partial Q(s_t,a_t;w)}{\partial w} |_{ w=w_t}\)

    4. 由於執行了動作 \(a_t\)，環境會更新狀態為 \(s_{t+1}\)，並給出獎勵\(r_t\)。

    5. 求出TD target：\(y_t = r_t + \gamma \cdot \mathop{max}\limits_{a} Q(s_{t+1},a_t;w）\)

    6. 做一次梯度下降更新引數 w , \(w_{t+1} = w_t - \alpha \cdot (q_t-y_t) \cdot d_t\)

    7. 更新迭代...

x. 參考教學