CANN運算元:利用迭代器高效實現Tensor資料切割分塊處理
摘要:本文以Diagonal運算元為例,介紹並詳細講解如何利用迭代器對n維Tensor進行基於位置座標的大批次資料讀取工作。
本文分享自華為雲社群《CANN運算元:利用迭代器高效實現Tensor資料切割分塊處理》,作者: CatherineWang 。
任務場景及目標
在CANN aicpu運算元開發實現中,經常需要對n維Tensor進行切片(slice)、切塊(dice)、轉置(transpose)、交換指定維度資料(shuffle)等操作。上述操作實質上是按照指定規律依次進行資料讀取,並將讀取到的資料寫入新的資料地址中。
本文以Diagonal運算元為例,介紹並詳細講解如何利用迭代器對n維Tensor進行基於位置座標的大批次資料讀取工作。
Diagonal運算元希望對指定兩個維度的資料進行對角元素的提取,最終返回張量的對角線元素。本質上該運算元通過屬性dim1和dim2確定一個矩陣,返回該矩陣的對角元素(存在偏移量offset),並將其放置在最後一維。非dim1和dim2的維度,將會被當成batch維度處理。
常規方案:
方案一:將shape為s,元素個數為numel的 輸入Tensor:x轉化為Eigen::Tensor:eigen_x;對eigen_x進行shuffle操作,將dim1和dim2換至倒數第二和倒數第一維;通過reshape操作將eigen_x變化為一個三維Eigen::Tensor:reshape_x,shape=(numel/ s[dim1]/s[dim2],s[dim1],s[dim2]);對後兩維資料取對角元素,並將最終資料賦值給輸出資料地址。注意:由於Eigen::Tensor<typename T, int NumIndices_>不能夠動態設定維度,即NumIndices_項必須是一個具體的值,因此需要提前定義對應維度的Eigen::Tensor備用。
方案二:對於一個n維的Tensor,利用n層for迴圈進行資料的定位讀取,並取對角值。
可以看出上述兩個方案對動態大小的輸入計算實現處理都較為繁瑣,需要提前分情況設定對應維度的Eigen::Tensor或是for迴圈邏輯結構,即存在維數限制。
準備知識及分析
我們知道再AICPU中,對於一個Tensor,我們能夠通過GetTensorShape、GetData等函數獲得Tensor形狀大小、具體資料地址等資訊。但我們不能通過位置座標的形式直接獲得指定位置的資料值。
1.步長
首先介紹步長(stride)這一概念(對這部分知識已掌握的可以直接跳轉下一部分內容)。stride是在指定維度dim中從一個元素跳到下一個元素所必需的步長。例如,對於一個shape=(2, 3, 4, 5)的Tensor,其stride=(60, 20, 5, 1)。因此如果想要獲取到上述Tensor中位置座標為[1, 2, 1, 3]的資料,只需要找到資料地址中第108(=60*1+20*2+5*1+3)位對應值。
2.迭代器
定義迭代器PositionIterator,包含私有成員pos_和shape_,其中pos_為初始位置,shape_為標準形狀。通過過載++符號,對pos_進行修改,實現迭代器的自增操作。基於上述迭代器,可以實現對給定的shape依次取位元運算。如給定對於給定的shape=(d_1,d_2,…,d_n),從初始位置(0,0,…,0)開始,依次取(0,0,…,0,0), (0,0,…,0,1),…,(0,0,…,0,d_n-1), (0,0,…,1,0), (0,0,…,1,1),…, (d_1 - 1,d_2 - 1,…,d_{n-1}-1,d_{n}-1).
事實上,可以將上述迭代器理解為一種進位制,對於給定的標準形狀shape_=(d_1,d_2,…,d_n),第i位運算時便是逢d_i進1。同時通過PositionIterator .End()控制迭代器的結束。具體實現如下:
template <typename T> class PositionIterator { public: PositionIterator(){}; ~PositionIterator(){}; PositionIterator(std::vector<T> stt, std::vector<T> sh) { if (stt.size() != sh.size()) { PositionIterator(); } else { for (unsigned int i = 0; i < sh.size(); i++) { if (stt[i] >= sh[i]) { PositionIterator(); } } pos_ = stt; shape_ = sh; } } PositionIterator operator++() { pos_[shape_.size() - 1] += 1; for (unsigned int i = shape_.size() - 1; i > 0; i--) { if (pos_[i] / shape_[i] != 0) { pos_[i - 1] += pos_[i] / shape_[i]; pos_[i] = pos_[i] % shape_[i]; } } return *this; } bool End() { if (pos_[0] != shape_[0]) { return false; } return true; } std::vector<T> GetPos() { return pos_; } std::vector<T> GetShape() { return shape_; } private: std::vector<T> pos_; std::vector<T> shape_; };
Diagonal運算元的實現
利用迭代器,在一般情況下,我們只需要兩層for迴圈,便可以實現Diagonal運算元的計算過程。第一層for迴圈用於確定除dim1和dim2維度的位置座標,第二層for迴圈用於對dim1和dim2對應維度確定對角元素位置,通過這樣的兩層for迴圈,便可將對角元素位置確定。通過這樣的取值處理,相較於Eigen實現思路,計算速度有著明顯的提升,且無維度限制,st測試結果對比如下:
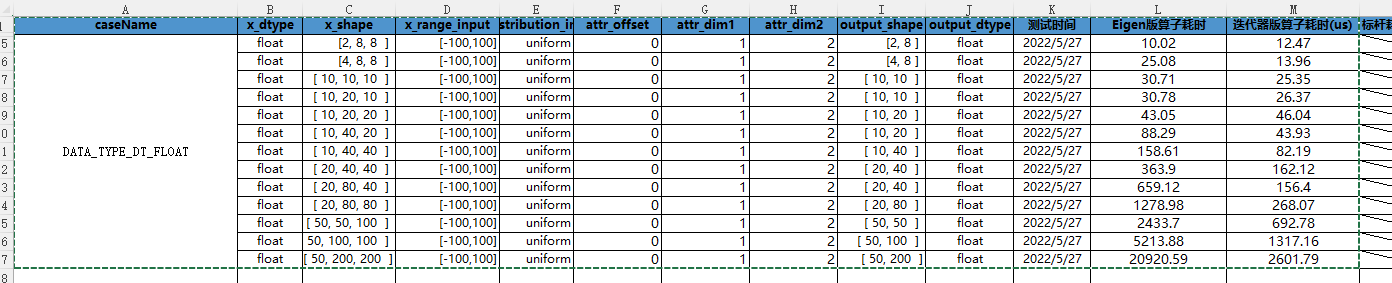
具體實現可參見如下程式碼:
template <typename T> uint32_t DiagonalCpuKernel::DoComputeType(CpuKernelContext &ctx, const int64_t &offset, const int64_t &dim1, const int64_t &dim2) { // Get the inuput and output Tensor *input_x = ctx.Input(0); Tensor *y = ctx.Output(0); // Get some information of input auto x_shape = input_x->GetTensorShape(); std::vector<int64_t> x_shape_ = x_shape->GetDimSizes(); const int64_t x_dim = x_shape->GetDims(); auto dataptr = reinterpret_cast<T *>(ctx.Input(0)->GetData()); auto y_dataptr = reinterpret_cast<T *>(y->GetData()); // Compute // 首先計算出對角線元素個數 int64_t dsize = OffsetSize(offset, dim1, dim2, x_shape_); // 生成輸入Tensor的步長向量x_stride std::vector<int64_t> x_stride = ConstructStride<int64_t>(x_shape_); // 分情況討論,2維和大於2維的情況 if (x_dim != N2) { //set the vx_shape and vx_stride // 生成x_shape和x_stride中除去dim1和dim2對應值的vx_shape與vx_stride std::vector<int64_t> vx_shape, vx_stride; for (unsigned int tmp_dim = 0; tmp_dim < x_shape_.size(); tmp_dim++) { if (tmp_dim != dim1 && tmp_dim != dim2) { vx_shape.push_back(x_shape_[tmp_dim]); vx_stride.push_back(x_stride[tmp_dim]); } } // set the y_shape, y_stride, vy_stride // 生成輸出Tensor的形狀及步長向量:y_shape和y_stride std::vector<int64_t> y_shape = vx_shape; y_shape.push_back(dsize); std::vector<int64_t> y_stride = ConstructStride<int64_t>(y_shape); // 生成輸出Tensor的出去最後一維的步長向量:vy_stride std::vector<int64_t> vy_stride = y_stride; vy_stride.pop_back(); // 讀取對角資料 std::vector<int64_t> v_start(vx_shape.size(), 0); for (PositionIterator<int64_t> myiter(v_start, vx_shape); !myiter.End(); ++myiter) { // 利用迭代器確定除dim1和dim2維度的位置座標 auto p = myiter.GetPos(); // 通過步長向量和位置座標計算出輸入和輸出的基礎位置值base_pos1和outbase_pos int64_t base_pos1 = MulSum<int64_t>(p, vx_stride); int64_t outbase_pos = MulSum<int64_t>(p, vy_stride); for (int i = 0; i < dsize; i++) { // 結合前面計算出的基礎位置值,對dim1和dim2對應維度確定對角元素位置,並賦值給輸出資料地址(get_data涉及對上對角還是下對角取元素,不影響對迭代器作用的理解) int64_t base_pos2 = i * (x_stride[dim1] + x_stride[dim2]); int64_t arr[N2] = {x_stride[dim1], x_stride[dim2]}; y_dataptr[outbase_pos + i] = get_data(base_pos1 + base_pos2, offset, arr, dataptr); } } } else { for (int i = 0; i < dsize; i++) { int64_t base_pos = i * (x_stride[dim1] + x_stride[dim2]); int64_t arr[N2] = {x_stride[dim1], x_stride[dim2]}; y_dataptr[i] = get_data(base_pos, offset, arr, dataptr); } } return KERNEL_STATUS_OK; }
迭代器的其他用法
1、資料切條:如Sort運算元中,用迭代器對Tensor資料關於tmp_axis維度進行取條,以進行後續的排序操作。
for (position_iterator<int64_t> mit(v_start, v_shape); !mit.end(); ++mit) { auto p = mit.get_pos(); int axis_len = input_shape_[tmp_axis]; std::vector<ValueIndex<T>> data_(axis_len); int base_pos = mul_sum<int64_t>(p, v_stride); for (int32_t i = 0; i < axis_len; i++) { data_[i].value = x_dataptr[base_pos + i * input_stride[tmp_axis]]; data_[i].index = i; }
2、資料切塊:切塊處理可以利用兩個迭代器迴圈疊加,也可以利用一個迭代器和兩個座標位置for迴圈
3、關於指定維度dim,對Tensor降維拆分為N子Tensor:如UniqueConsecutive運算元中,首先需要關於屬性axis維,將原本的Tensor資料拆分為input_shape[axis]個子Tensor(此處用vector儲存Tensor中的資料)。
std::vector<std::vector<T1>> data_; for (int64_t i = 0; i < dim0; i++) { std::vector<T1> tmp_v1; for (PositionIterator<int64_t> mit(v_start, v_shape); !mit.End(); ++mit) { auto pos = mit.GetPos(); tmp_v1.push_back( x_dataptr[MulSum<int64_t>(pos, v_stride) + i * input_stride[axis]]); } data_.push_back(tmp_v1); }