機器學習基礎:用 Lasso 做特徵選擇
大家入門機器學習第一個接觸的模型應該是簡單線性迴歸,但是在學Lasso時往往一帶而過。其實 Lasso 迴歸也是機器學習模型中的常青樹,在工業界應用十分廣泛。在很多專案,尤其是特徵選擇中都會見到他的影子。
Lasso 給簡單線性迴歸加了 L1 正則化,可以將不重要變數的係數收縮到 0 ,從而實現了特徵選擇。本文重點也是在講解其原理後演示如何用其進行特徵選擇,希望大家能收穫一點新知識。
lasso 原理
Lasso就是在簡單線性迴歸的目標函數後面加了一個1-範數
回憶一下:線上性迴歸中如果引數θ過大、特徵過多就會很容易造成過擬合,如下如所示:
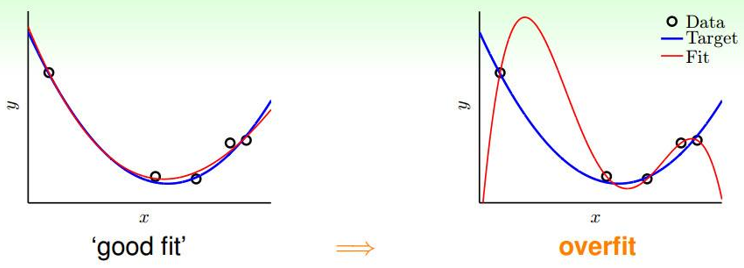
李宏毅老師的這張圖更有視覺衝擊力

為了防止過擬合(θ過大),在目標函數$J(\theta)$後新增複雜度懲罰因子,即正則項來防止過擬合,增強模型泛化能力。正則項可以使用L1-norm(Lasso)、L2-norm(Ridge),或結合L1-norm、L2-norm(Elastic Net)。
lasso迴歸的代價函數
$$
J(\theta)=\frac{1}{2}\sum_{i}{m}(y{(i)}-\theta Tx{(i)})^2+\lambda \sum_{j}^{n}|\theta_j|
$$
矩陣形式:
$$
J(\mathbf\theta) = \frac{1}{2n}(\mathbf{X\theta} - \mathbf{Y})^T(\mathbf{X\theta} - \mathbf{Y}) + \alpha||\theta||_1
$$
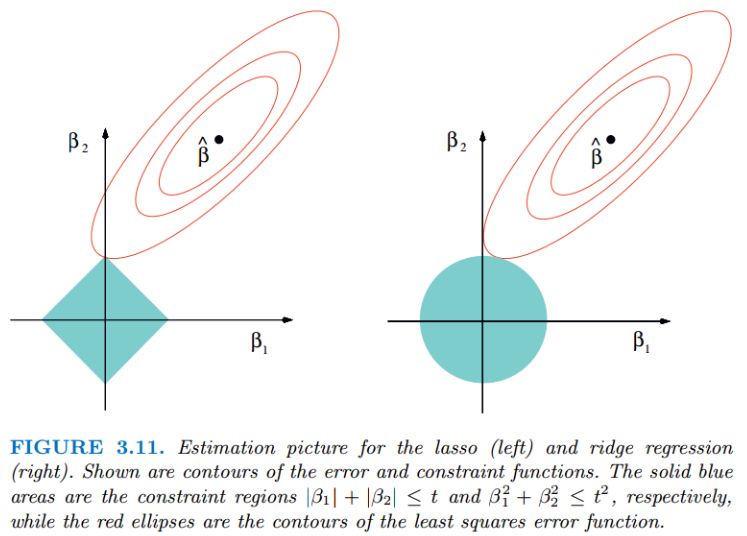
無論嶺迴歸還是lasso迴歸,本質都是通過調節$λ$來實現模型誤差和方差的平衡調整。紅色的橢圓和藍色的區域的切點就是目標函數的最優解,可以看出Lasso的最優解更容易切到座標軸上,形成稀疏結果(某些係數為零)。
Ridge迴歸在不拋棄任何一個特徵的情況下,縮小了迴歸係數,使得模型相對而言比較的穩定,但和Lasso迴歸比,這會使得模型的特徵留的特別多,模型解釋性差。
今天我們的重點是Lasso,優化目標是:
$(1 / (2 * n_samples)) * ||y - Xw||^2_2 + alpha * ||w||_1$
上式不是連續可導的,因此常規的解法如梯度下降法、牛頓法、就沒法用了。常用的方法:座標軸下降法與最小角迴歸法(Least-angle regression (LARS))。
這部分就不展開了,感興趣的同學可以看下劉建平老師的文章《Lasso迴歸演演算法: 座標軸下降法與最小角迴歸法小結 》,這裡不過多贅述。
https://www.cnblogs.com/pinard/p/6018889.html
想深入研究,可以看下Coordinate Descent和LARS的論文
https://www.stat.cmu.edu/~ryantibs/convexopt-S15/lectures/22-coord-desc.pdf
https://arxiv.org/pdf/math/0406456.pdf
scikit-learn 提供了這兩種優化演演算法的Lasso實現,分別是
sklearn.linear_model.Lasso(alpha=1.0, *, fit_intercept=True,
normalize='deprecated', precompute=False, copy_X=True,
max_iter=1000, tol=0.0001, warm_start=False,
positive=False, random_state=None, selection='cyclic')
sklearn.linear_model.lars_path(X, y, Xy=None, *, Gram=None,
max_iter=500, alpha_min=0, method='lar', copy_X=True,
eps=2.220446049250313e-16, copy_Gram=True, verbose=0,
return_path=True, return_n_iter=False, positive=False)
用 Lasso 找到特徵重要性
在機器學習中,面對海量的資料,首先想到的就是降維,爭取用盡可能少的資料解決問題,Lasso方法可以將特徵的係數進行壓縮並使某些迴歸係數變為0,進而達到特徵選擇的目的,可以廣泛地應用於模型改進與選擇。

scikit-learn 的Lasso實現中,更常用的其實是LassoCV(沿著正則化路徑具有迭代擬合的套索(Lasso)線性模型),它對超引數$\alpha$使用了交叉驗證,來幫忙我們選擇一個合適的$\alpha$。不過GridSearchCV+Lasso也能實現調參,這裡就列一下LassoCV的引數、屬性和方法。
### 引數
eps:路徑的長度。eps=1e-3意味著alpha_min / alpha_max = 1e-3。
n_alphas:沿正則化路徑的Alpha個數,預設100。
alphas:用於計算模型的alpha列表。如果為None,自動設定Alpha。
fit_intercept:是否估計截距,預設True。如果為False,則假定資料已經中心化。
tol:優化的容忍度,預設1e-4:如果更新小於tol,優化程式碼將檢查對偶間隙的最優性,並一直持續到它小於tol為止
cv:定交叉驗證拆分策略
### 屬性
alpha_:交叉驗證選擇的懲罰量
coef_:引數向量(目標函數公式中的w)。
intercept_:目標函數中的截距。
mse_path_:每次摺疊不同alpha下測試集的均方誤差。
alphas_:對於每個l1_ratio,用於擬合的alpha網格。
dual_gap_:最佳alpha(alpha_)優化結束時的雙重間隔。
n_iter_ int:座標下降求解器執行的迭代次數,以達到指定容忍度的最優alpha。
### 方法
fit(X, y[, sample_weight, check_input]) 用座標下降法擬合模型。
get_params([deep]) 獲取此估計器的引數。
path(X, y, *[, l1_ratio, eps, n_alphas, …]) 計算具有座標下降的彈性網路徑。
predict(X) 使用線性模型進行預測。
score(X, y[, sample_weight]) 返回預測的確定係數R ^ 2。
set_params(**params) 設定此估算器的引數。
Python實戰
波士頓房價資料為例
## 匯入庫
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import Lasso
import warnings
warnings.filterwarnings('ignore')
## 讀取資料
url = r'F:\100-Days-Of-ML-Code\datasets\Regularization_Boston.csv'
df = pd.read_csv(url)
scaler=StandardScaler()
df_sc= scaler.fit_transform(df)
df_sc = pd.DataFrame(df_sc, columns=df.columns)
y = df_sc['price']
X = df_sc.drop('price', axis=1) # becareful inplace= False
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)
Lasso調引數,主要就是選擇合適的alpha,上面提到LassoCV,GridSearchCV都可以實現,這裡為了繪圖我們手動實現。
alpha_lasso = 10**np.linspace(-3,1,100)
lasso = Lasso()
coefs_lasso = []
for i in alpha_lasso:
lasso.set_params(alpha = i)
lasso.fit(X_train, y_train)
coefs_lasso.append(lasso.coef_)
plt.figure(figsize=(12,10))
ax = plt.gca()
ax.plot(alpha_lasso, coefs_lasso)
ax.set_xscale('log')
plt.axis('tight')
plt.xlabel('alpha')
plt.ylabel('weights: scaled coefficients')
plt.title('Lasso regression coefficients Vs. alpha')
plt.legend(df.drop('price',axis=1, inplace=False).columns)
plt.show()
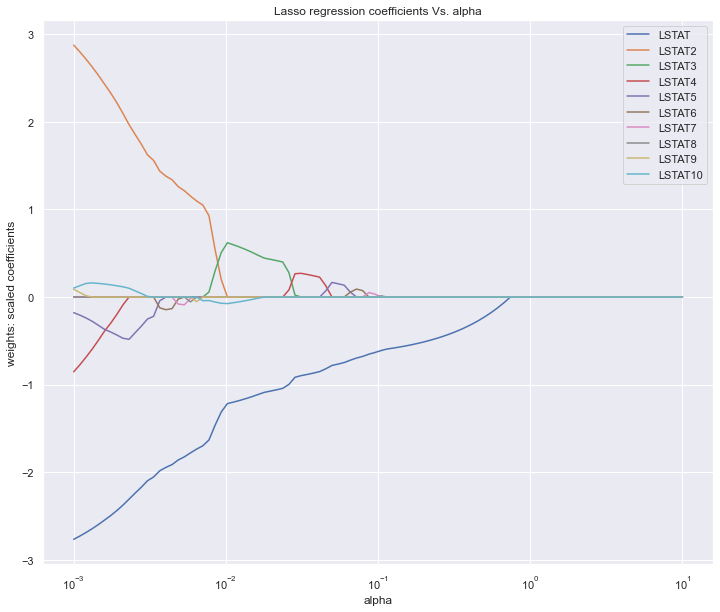
圖中展示的是不同的變數隨著alpha懲罰後,其係數的變化,我們要保留的就是係數不為0的變數。alpha值不斷增大時係數才變為0的變數在模型中越重要。
我們也可以按係數絕對值大小倒序看下特徵重要性,可以設定更大的alpha值,就會看到更多的係數被壓縮為0了。
lasso = Lasso(alpha=10**(-3))
model_lasso = lasso.fit(X_train, y_train)
coef = pd.Series(model_lasso.coef_,index=X_train.columns)
print(coef[coef != 0].abs().sort_values(ascending = False))
LSTAT2 2.876424
LSTAT 2.766566
LSTAT4 0.853773
LSTAT5 0.178117
LSTAT10 0.102558
LSTAT9 0.088525
LSTAT8 0.001112
dtype: float64
lasso = Lasso(alpha=10**(-2))
model_lasso = lasso.fit(X_train, y_train)
coef = pd.Series(model_lasso.coef_,index=X_train.columns)
print(coef[coef != 0].abs().sort_values(ascending = False))
LSTAT 1.220552
LSTAT3 0.625608
LSTAT10 0.077125
dtype: float64
或者直接畫個柱狀圖
fea = X_train.columns
a = pd.DataFrame()
a['feature'] = fea
a['importance'] = coef.values
a = a.sort_values('importance',ascending = False)
plt.figure(figsize=(12,8))
plt.barh(a['feature'],a['importance'])
plt.title('the importance features')
plt.show()
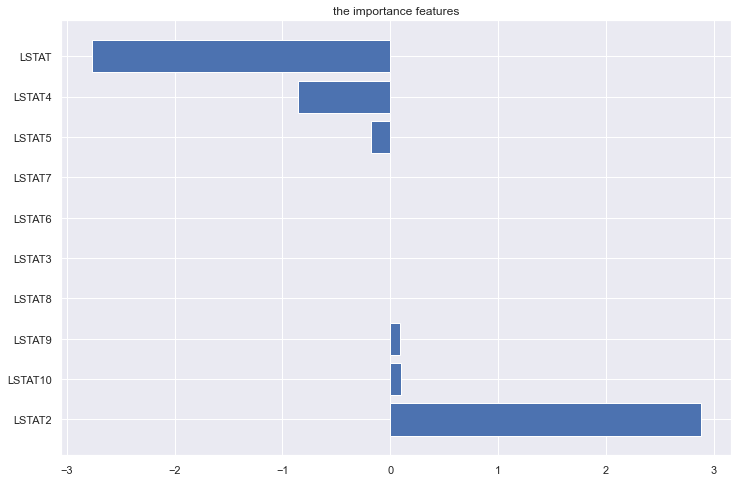
總結
Lasso迴歸方法的優點是可以彌補最小二乘估計法和逐步迴歸區域性最優估計的不足,可以很好地進行特徵的選擇,有效地解決各特徵之間存在多重共線性的問題。
缺點是當存在一組高度相關的特徵時,Lasso迴歸方法傾向於選擇其中的一個特徵,而忽視其他所有的特徵,這種情況會導致結果的不穩定性。
雖然Lasso迴歸方法存在弊端,但是在合適的場景中還是可以發揮不錯的效果的。
reference
https://www.biaodianfu.com/ridge-lasso-elasticnet.html
https://machinelearningcompass.com/machine_learning_models/lasso_regression/
https://www.cnblogs.com/pinard/p/6004041.html
https://www.biaodianfu.com/ridge-lasso-elasticnet.html