11 GloDyNE Global Topology Preserving Dynamic Network Embedding

link:http://arxiv.org/abs/2008.01935

Abstract

目前大多數現有的DNE方法的思想是捕捉最受影響的節點(而不是所有節點)或周圍的拓撲變化，並相應更新節點嵌入。

這種近似雖然可以提高效率，但由於沒有考慮通過高階近似傳播和接收累積拓撲變化的非活躍子網路，因此不能有效地保持動態網路在每個時間步的全域性拓撲。

為了應對這一挑戰，我們提出了一種新的節點選擇策略，在網路上多樣化地選擇代表節點，這個方法是種新的增量學習正規化——基於Skip-Gram的協調嵌入方法。

Conclusion

本文提出了一種新的DNE方法GloDyNE，該方法通過擴充套件SGNS模型到增量學習正規化，旨在有效地更新節點嵌入，同時更好地保持動態網路在每個時間步的全域性拓撲。與以往的DNE方法不同，提出了一種新的節點選擇策略，在網路中多樣化地選擇代表節點，並額外考慮不活躍的子網路，以更好地保持全域性拓撲。

GloDyNE也可以看作是一個基於SGNS模型增量學習正規化的通用DNE框架。通過這個框架，可以設計不同的節點選擇策略，為特定應用程式的節點嵌入保留其他理想的拓撲特徵。另一方面，選擇不同節點的思想可以適應現有的其他DNE方法，以更好地保持全域性拓撲。

Figure and table

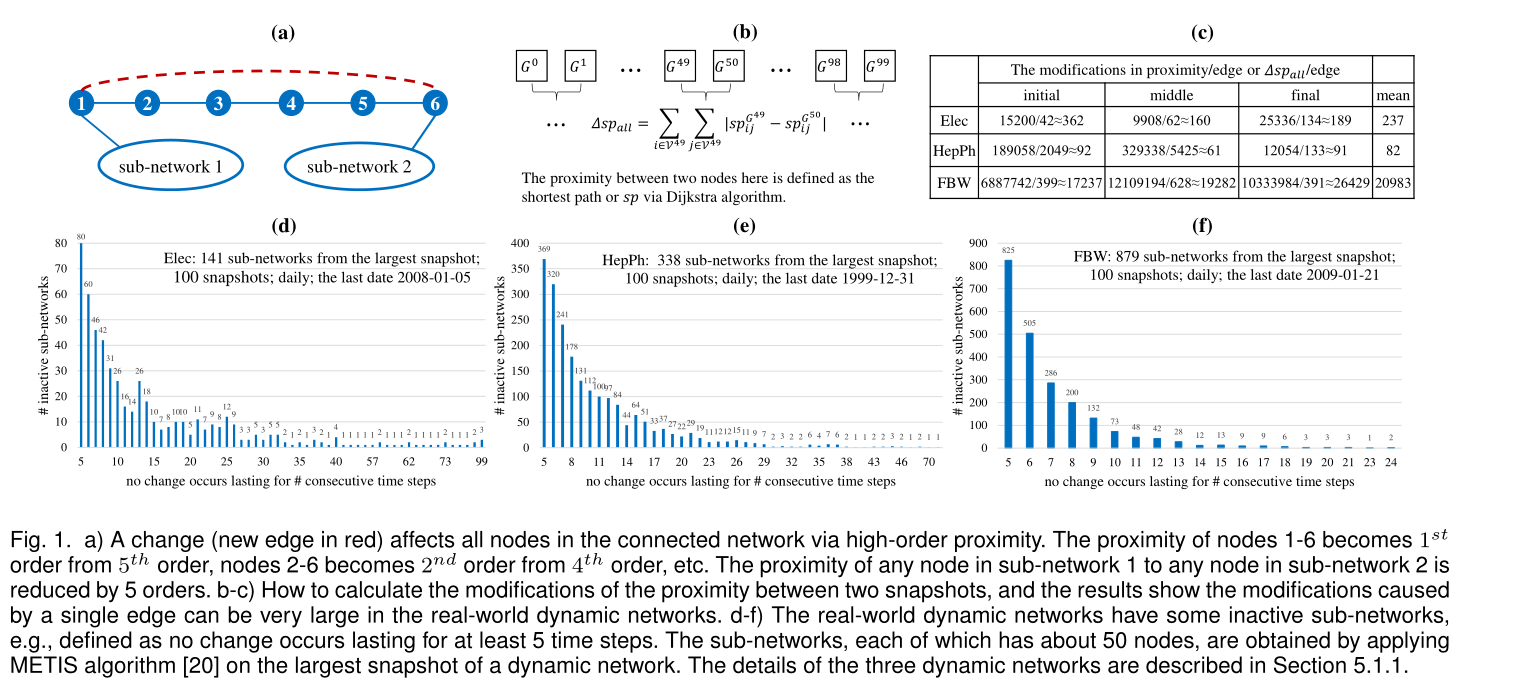
圖1

a) 通過高階近似下，一個改變（紅色的新邊）會影響聯通圖的所有節點。節點1-6的接近程度由5階變為1階，結點2-6從4階變成了2階，以此類推。則可得子網路1中的任意節點與子網路2中的任意節點的接近度降低了5階

b-c)如何計算兩個快照之間的接近程度的修改，結果表明，在真實的動態網路中，由單個邊緣引起的修改可以非常大。

d-f)現實世界的動態網路有一些不活躍的子網路，例如，定義為持續至少5個時間步沒有發生變化。在動態網路的最大快照上應用METIS演演算法[20]得到每個子網約有50個節點。三種動態網路的詳細描述在5.1.1節中。

表1 圖重構的sota

表2 在連結預測下的AUC對比

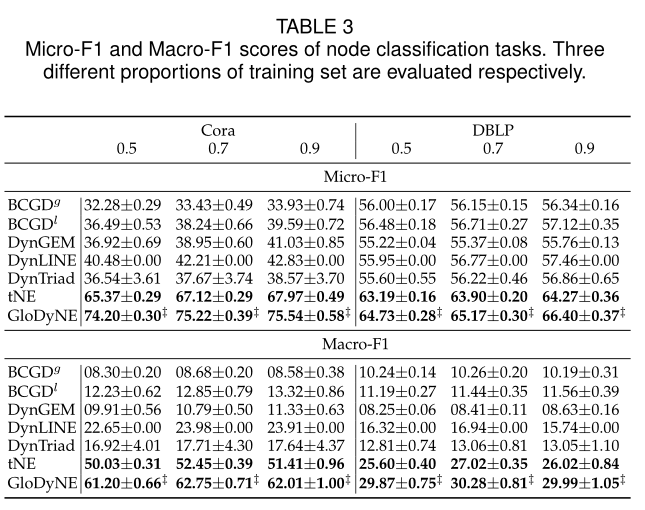
表3 節點分類任務的Micro-F1和Macro-F1得分。分別評價三種不同比例的訓練集。

表4 執行時間對比

圖2 AUC/時間的綜合對比

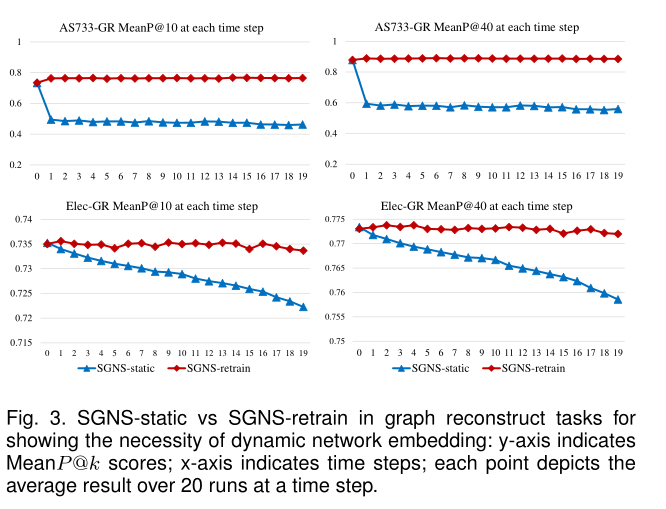
圖3 圖重構任務中的SGNS-static 和 SGNS-retrain表示動態網路嵌入的必要性。

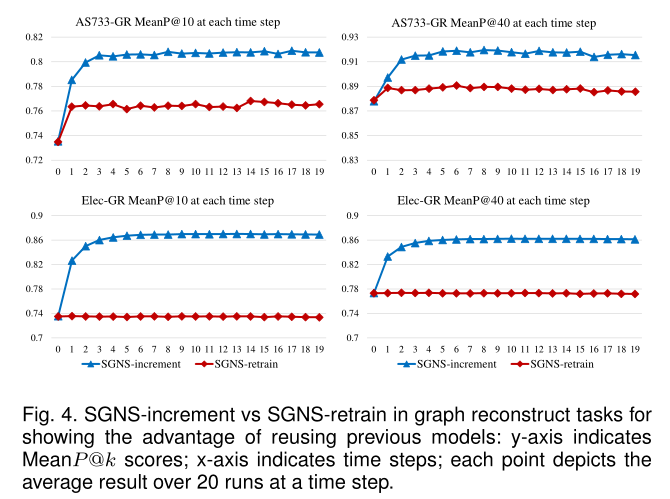
圖4 圖重構任務中的SGNS-increment 和 SGNS-retrain，展示了重用先前模型的優勢

圖5 第一行6個子圖是在Elec上應用GloDyNE分別獲得8 - 13六個連續時間步的節點嵌入。第二行是SGNS-retrain。為了視覺化嵌入，我們進一步將它們從128個維度投影到2個維度。

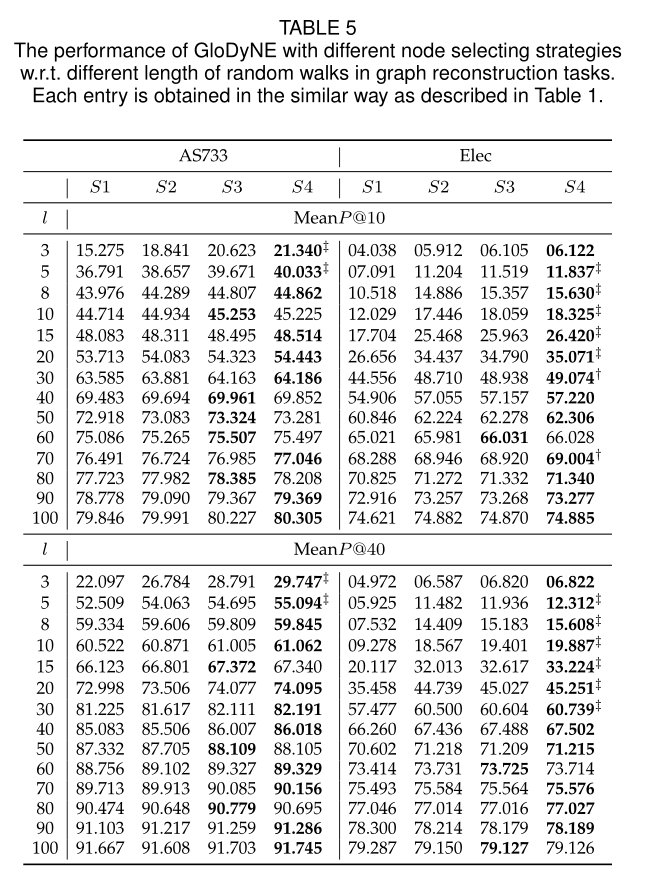
表5 不同節點選擇策略下的GloDyNE在圖重構任務中的效能。

圖6 GloDyNE的有效性(藍色對應左y軸)和效率(紅色對應右y軸)。不同的α (x軸)決定所選節點的數量

Introduction

以往的動態嵌入是希望只對受影響的節點進行嵌入更新以保證效率和效能的平衡，但是這樣會導致不能有效地保持動態網路在每個時間步長的全域性拓撲，具體來說，任何變化，如邊的增加或刪除，都會影響到連線網路中的所有節點，並通過圖1 a-c)所示的高階近似程度極大地改變網路上節點之間的近似程度。另一方面，如圖1 d-f)所示，真實世界的動態網路通常有一些不活躍的子網路，這些子網路在幾個時間步驟中沒有發生變化。總的來說，現有的DNE方法只關注受影響最嚴重的節點(屬於活動子網路)，而不考慮非活動子網路，忽略了通過高階近似傳播到非活動子網路的累積拓撲變化

為了解決這一問題，本文提出的全域性拓撲保持動態網路嵌入(GloDyNE)方法首先將當前網路劃分為較小的子網路，每個子網路中選擇一個具有代表性的節點，以保證所選節點的多樣性。每個子網路的代表性節點通過概率分佈在每個子網路內的所有節點上進行抽樣，使累計拓撲變化較大的節點獲得較高的概率。接著GloDyNE通過截斷隨機遊走來捕獲所選節點周圍的最新拓撲，然後根據skim-gram負取樣(SGNS)模型和增量學習正規化及時更新節點嵌入。

本文貢獻如下

1 證明了在真實世界下，動態網路中存在非活躍子圖。並且發現在現有的DNE方法下，都存在有如何保持全域性拓撲的問題。

2 為了更好地儲存全域性拓撲，與之前所有的DNE方法不同，建議同時考慮非活動子網中累積的拓撲變化。提出了一種新的節點選擇策略，可以在網路中多樣化地選擇具有代表性的節點。

3 進一步開發了一種新的DNE方法或框架，即GloDyNE，它將基於隨機遊走和Skip-Gram的網路嵌入方法擴充套件為一種具有自由超引數的增量學習正規化，可用於控制每個時間步的選定節點數量。

4 sota

Method

3 NOTATION AND PROBLEM DEFINITION

定義1 靜態網路

用\(G=\{\mathcal{V},\mathcal{E}\}\)表示靜態網路，其中\(\mathcal{v}\)表示為一組\(|\mathcal{V}|\)個節點的集合，\(\mathcal{E}\)表示為一組\(|\mathcal{E}|\)條邊的集合。

\(G\)的鄰接矩陣\(W \in \mathbb{R}^{|\mathcal{V} \times \mathcal{V}|}\)，其中\(w_{ij}\)表示為一對節點\((v_i,v_j)\)的邊 \(e_{ij}\)的權重，如果\(w_{ij} = 0\)，則意味著兩節點之間無邊

定義2 動態網路

將動態網路\(\mathcal{G}\)定義為一組在\(t\)時間下的靜態圖快照\(G^t\)，記做\(\mathcal{G} = \{ G^0, G^1 , ... , G^t, G^{t+1}, ... , \}\) 每個快照\(G^t\)都可以看做是靜態圖。

定義3 靜態網路嵌入

目的是尋找一個對映函數\(Z = f(G)\)，其中\(Z \in \mathbb{R}^{|V|×d}, d \ll |\mathcal{V}|\)，每個行向量\(Z_i∈\mathbb{R}^d\)是\(v_i\)的節點嵌入，使得\(Z\)中節點嵌入的兩兩相似度最好地保留了G中節點的兩兩拓撲相似度。

定義4 動態網路嵌入

在增量學習正規化下，動態圖的嵌入被表示為\(Z^{t}=f^{t}\left(G^{t}, G^{t-1}, f^{t-1}, Z^{t-1}\right)\)，其中\(Z^{t} \in \mathbb{R}^{\left|\mathcal{V}^{t}\right| \times d}\)是最新的節點嵌入，\(f^{t-1}\)和\(Z^{t-1}\)分別為上一個時間步的模型和嵌入。動態圖的嵌入的主要目標是在每個當前時間步\(t\)上高效地更新節點嵌入，使\(Z^t\)中節點嵌入的兩兩相似度最好地保留了\(G^t\)中節點的兩兩拓撲相似度。

定義5 快照的子網路

定義\(G^t_k\)表示快照\(G^t\)中的第\(k\)個子網路，一個快照\(G^t\)在網路分割區後的所有子網不重疊，寫做\(\mathcal{V}_{m}^{t} \cap \mathcal{V}_{n}^{t}=\emptyset, \forall m \neq n\)，它們的節點集應該滿足\(\mathcal{V}^{t}=\bigcup_{k} \mathcal{V}_{k}^{t}\)。

4 THE PROPOSED METHOD

4.1 Method Description

4.1.1 Step 1. Partition A Network

為了實現分割快照\(G^t\)的非活躍子網路，需要將\(G^t\)劃分為多個子網路\(G^t_1, G^t_2, ..., G^t_K\)，其中K為一個快照的子網數。這些子網路不重疊，並且按照定義5的定義覆蓋原始快照中的所有節點，這樣後面的步驟2可以從每個子網路中選擇唯一的節點，後面的步驟3可以更容易地根據每個子網路中選擇的節點來探索整個快照\(G^t\)。因此，使用網路分割區演演算法（Recent advances in graph partitioning）來實現。最常見的目標函數是最小化邊緣切口，即

\[\min \sum_{1 \leq m, n \leq K}\left\{w_{i, j}^{t} \mid v_{i}^{t} \in \mathcal{V}_{m}^{t}, v_{j}^{t} \in \mathcal{V}_{n}^{t},\left(v_{i}^{t}, v_{j}^{t}\right) \in \mathcal{E}^{t}\right\}(1) \]

其中下標\(i, j\)表示節點ID, \(m, n\)表示子網ID。注意，式(1)應該受到兩個約束\(\mathcal{V}_{m}^{t} \cap \mathcal{V}_{n}^{t}=\emptyset, \forall m \neq n\) 和 \(\mathcal{V}^{t}=\bigcup_{k} \mathcal{V}_{k}^{t}\)（定義5中的約束）

此外，還引入了一個均衡子網的附加約束，使所有子網之間的節點數量相似，便於後續步驟公平地探索所有子網，從而更好地保持全域性拓撲結構。關於平衡子網路的第三個約束可以定義為

\[\forall k \in\{1, \ldots, K\},\left|\mathcal{V}_{k}^{t}\right| \leq(1+\epsilon) \frac{\left|\mathcal{V}^{t}\right|}{K}(2) \]

其中\(|\mathcal{V}^t_k|\)是\(G^t_k\)中的節點數，\(\epsilon\)為公差引數（調整子網路節點數）,注意，如果\(\epsilon\)為0時，網路分割區完全平衡。在實踐中，\(\epsilon\)設定為一個小的數位，以允許輕微節點數量浮動。然而，這樣一個\((K,\epsilon)\)平衡的網路分割區是一個NP-hard問題。為了解決這個問題，本文采用了METIS演演算法。大致有三個步驟。

首先是粗化階段，將原始網路遞迴轉化為一系列越來越小的抽象網路，通過將具有共同鄰居的節點壓縮為一個壓縮節點，直到抽象網路足夠小。

其次是劃分階段，在最小的抽象網路上應用K路劃分演演算法，得到K個子網路的初始劃分

第三，非粗化階段，遞迴地將最小的抽象網路擴充套件回原始網路，同時遞迴地交換相鄰兩個子網路之間的子網路邊界處的摺疊節點(或最後交換原始節點)，以使式(1)所示的邊割最小化。

4.1.2 Step 2. Select Representative Nodes

為了保證所選節點在快照\(G^t\)上分佈的多樣性，一種想法是從每個子網中選擇一個代表性節點。因此，選擇的節點總數為K。

也可設\(K = \alpha|V_t|\)，使α可以自由控制選擇的節點總數，在有效性和效率之間進行權衡。

現在的問題變成了如何從子網中選擇一個有代表性的節點。根據最新的DNE工作，選擇受邊緣流影響較大的節點更新它們的嵌入，因為它們的拓撲改變較大。同樣，在本工作中，待選擇的代表性節點也傾向於拓撲變化較大的節點。定義節點\(v_i^t\)在快照\(G^t\)下的累計拓撲變化為

\[\begin{aligned} S\left(v_{i}^{t}\right) &=\frac{\left|\Delta \mathcal{E}_{i}^{t}\right|+\mathcal{R}_{i}^{t-1}}{\operatorname{Deg}\left(v_{i}^{t-1}\right)} \\ &=\frac{\left|\mathcal{N}\left(v_{i}^{t}\right) \cup \mathcal{N}\left(v_{i}^{t-1}\right)-\mathcal{N}\left(v_{i}^{t}\right) \cap \mathcal{N}\left(v_{i}^{t-1}\right)\right|+\mathcal{R}_{i}^{t-1}}{\operatorname{Deg}\left(v_{i}^{t-1}\right)} \end{aligned}(3) \]

其中\(\mathcal{R}_{i}^{t-1}\)儲存了\(v_i\)到\(t−1\)的累積變化(個人認為\(\mathcal{R}_{i}^{t-1}=\sum_{j=1}^{t-1}(S\left(v_{i}^{j}\right))\))。為了簡化，我們將\(G^t\)視為一個無向無權網路，因此\(v_i\)在\(t\)時的當前變化記為\(|\Delta\mathcal{E}_{i}^{t} |\)，可以通過對\(v_i\)的鄰居進行集合操作，如式(3)所示，它相當於計算當前邊流(edge streams)中帶有節點\(v_i\)的邊的數量\(\Delta\mathcal{E}_{i}^{t}\)。

然後用softmax做一次歸一化

\[P\left(v_{i}^{t}\right)=\frac{e^{S\left(v_{i}^{t}\right)}}{\sum_{v_{j}^{t} \in \mathcal{V}_{k}^{t}} e^{S\left(v_{j}^{t}\right)}} \quad \forall v_{i}^{t} \in \mathcal{V}_{k}^{t}(4) \]

注意，如果\(S\left(v_{i}^{t}\right)=0\), \(e^0 = 1\), \(P (v^t_i)\ne 0\)，那麼即使一個非活躍的子網路中所有節點都沒有變化，其概率分佈仍然是一個有效的均勻分佈。直觀地看，在一個子網路中，式(3)中給定的節點得分越高，該節點被選為該子網路代表節點的概率越大。由於從每個子網中選擇一個具有代表性的節點，因此所有被選擇的節點在整個快照中分散分佈，同時偏向於每個子網累積的較大的拓撲變化。

4.1.3 Step 3. Capture Topological Changes

給定步驟2中選擇的代表性節點，此步驟將解釋如何基於所選節點捕獲拓撲變化。由於所選節點的拓撲變化可以通過高階相似傳播到其他節點，因此採用截斷隨機遊走取樣(而不是邊取樣)策略來捕獲所選節點周圍(而不是節點上)的拓撲變化。具體來說，對於每個選定的節點，從選定的節點開始，進行\(r\)次長度為\(l\)的隨機遊走。對於隨機遊走，可能取樣到的下一個節點\(v^t_j\)根據其上一個節點的鄰居\(\mathcal{N}\left(v_{i}^{t}\right)\)的概率分佈進行抽樣

\[P\left(v_{j}^{t} \mid v_{i}^{t}\right)=\left\{\begin{array}{cc} \frac{w_{i j}^{t}}{\sum_{v_{j^{\prime}} \in \mathcal{N}\left(v_{i}^{t}\right)} w_{i j^{\prime}}^{t}} & \text { if } v_{j} \in \mathcal{N}\left(v_{i}^{t}\right) \\ 0 & \text { otherwise } \end{array}\right.(5) \]

累積變化用於長期處理節點在每個時間步變化很小的情況，對網路拓撲影響較大，但如果不記錄可能會被忽略。

如果要在等式3中考慮邊緣的權重，可使\(\left|\Delta \mathcal{E}_{i}^{t}\right|=\sum_{v_{j}^{t} \in \mathcal{N}\left(v_{i}^{t}\right)}\left|w_{i, j}^{t}-w_{i, j}^{t-1}\right|+\sum_{v_{j}^{t-1} \in\left(\mathcal{N}\left(v_{i}^{t-1}\right)-\mathcal{N}\left(v_{i}^{t}\right)\right)}\left|w_{i, j}^{t-1}\right|\)

其中第一項給定了在\(t\)時第\(i^\prime\)個鄰居的總權重變化

第二項給定了在\(t-1\)時呈現但未在\(t\)第\(i^\prime\)個鄰居的總權重變化，（若有鄰居節點不再連線，在第一項中則無法統計到鄰居消失帶來的影響）

運運算元|·|在集合上給出其基數，在標量上給出其絕對值。

4.1.4 Step 4. Update Node Embeddings

在步驟3之後，對所選節點周圍最新的拓撲資訊進行隨機遊走編碼。步驟4的目的是利用隨機遊動來更新節點嵌入。

通過一個長度為\(S+1+S\)滑動視窗的形式進行節點對\((v^t_{center+i},v^t_{center}), i \in [-S,+S]\)正取樣並加入集合\(\mathcal{D}^t\)。

假設Dt中節點對的觀測值是相互獨立的，則最大化\(\mathcal{D}^t\)中所有節點對的節點共現對數概率的目標函數為

\[\max \sum_{\left(v_{i}^{t}, v_{c}^{t}\right) \in \mathcal{D}^{t}} \log P\left(v_{i}^{t} \mid v_{c}^{t}\right)(6) \]

其中\(v_c^t\)是中心節點，\(v_c^i\)是\(1-S\)階近似的其他節點，與deepwalk將\(P\left(v_{i}^{t} \mid v_{c}^{t}\right)\)定義為softmax不同，本文將其視為一個二進位制分類問題，從而進一步降低複雜性。具體來說，它的目的是區分一個正樣本\((v^t_i, v^t_j) \in \mathcal{D}^t\)和q個負樣本\((v^t_i, v^t_{j^\prime})\)。觀察到一個正樣本\((v^t_i, v^t_j)\)的概率為

\[P\left(B=1 \mid v_{i}^{t}, v_{j}^{t}\right)=\sigma\left(Z_{i}^{t} \cdot Z_{j}^{t}\right)=\frac{1}{1+e^{Z_{i}^{t} \cdot Z_{j}^{t}}}(7) \]

其中\(Z^t_i\)表示為通過對映函數\(f^t(v^t_i)\)得到的節點嵌入表示，\(\cdot\) 操作符表示向量的點乘操作，\(P\left(B=1 \mid v_{i}^{t}, v_{j}^{t}\right)\)給出一個正樣本\((v^t_i, v^t_j)\)下正確預測的概率。同樣，觀察到負樣本\((v^t_i, v^t_{j^\prime})\)的概率為

\[P\left(B=0 \mid v_{i}^{t}, v_{j^{\prime}}^{t}\right)=1-\sigma\left(Z_{i}^{t} \cdot Z_{j^{\prime}}^{t}\right)=\frac{1}{1+e^{-Z_{i}^{t} \cdot Z_{j^{\prime}}^{t}}}=\sigma\left(-Z_{i}^{t} \cdot Z_{j^{\prime}}^{t}\right)(8) \]

其中\(P\left(B=0 \mid v_{i}^{t}, v_{j^{\prime}}^{t}\right)\)給出了給定負樣本\((v^t_i, v^t_{j^\prime})\)的負預測概率。

上面的SkipGram負取樣(SGNS)模型嘗試最大化\(\mathcal{D}^t\)中每個正樣本的\(P\left(B=1 \mid v_{i}^{t}, v_{j}^{t}\right)\)和每個正確樣本對應的\(q\)個負樣本的\(P\left(B=0 \mid v_{i}^{t}, v_{j^{\prime}}^{t}\right)\)，即

\[\max \log \sigma\left(Z_{i}^{t} \cdot Z_{j}^{t}\right)+\sum_{q} \mathbf{E}_{v_{j^{\prime}}^{t} \sim P_{\mathcal{D}^{t}}}\left[\log \sigma\left(-Z_{i}^{t} \cdot Z_{j^{\prime}}^{t}\right)\right](9) \]

其中\(q\)個負樣本來自一元模型分佈 (unigram distribution) 。SGNS的總體目標是將所有正取樣及其負取樣相加

\[\max \sum_{\left(v_{i}^{t}, v_{j}^{t}\right) \in \mathcal{D}^{t}} \#\left(v_{i}^{t}, v_{j}^{t}\right) E q \cdot(9)\ \ \ \ \ \ \ \ (10) \]

其中，\(\#(v^t_i, v^t_j)\)表示正樣本在\(\mathcal{D}^t\)中出現的次數。直觀地說，一對節點一起出現的頻率越高，它們的嵌入就應該越緊密。

最後，將上述SGNS模型擴充套件為增量學習正規化。GloDyNE的整體框架可以形式化為

\[Z^{t}=\left\{\begin{array}{ll} f^{0}\left(G^{0}, f_{r a n d}^{0}, Z_{\text {rand }}^{0}\right) & t=0 \\ f^{t}\left(G^{t}, G^{t-1}, f^{t-1}, Z^{t-1}\right) & t \geq 1 \end{array}\right.(11) \]

其中\(f^{t−1}\)是上一個時間步訓練的SGNS模型，

\(Z^t\)是通過索引運運算元直接從新訓練的\(f^t\)中獲取的當前嵌入矩陣，

如果沒有直接給出，\(G^{t−1}\)和\(G^t\)是生成邊流(edge stream)\(\Delta\mathcal{E}^t\)的兩個連續快照

4.2 Algorithm

在演演算法1中總結了GloDyNE的虛擬碼

Experiment

5 EMPIRICAL STUDIES

5.1 Experimental Settings

5.1.1 Datasets

AS733，Elec，FBW，HepPh，Cora，DBLP

5.1.2 Methods

BCGD^g,BCGD^l Scalable temporal latent space inference for link prediction in dynamic social networks

DynGEM

DynLINE Dynamic network embedding : An extended approach for skip-gram based network embedding,

DynTriad

tNE Node embedding over temporal graphs

5.2 Comparative Studies of Different Methods

在本節，圖重構任務被用來展示全域性拓撲儲存的能力，而鏈路預測任務和節點分類任務體現了全域性拓撲儲存的優點。為了保證公平性，我首先將每一種方法得到的節點嵌入分別取出，然後將它們提供給完全相同的下游任務。

5.2.1 Graph Reconstruction (GR)

sota見表1

5.2.2 Link Prediction (LP)

sota見表2

5.2.3 Node Classification (NC)

sota見表3

5.2.4 Walk-Clock Time During Embedding

sota見表4

5.2.5 Effectiveness and Efficiency

效能和效率對比圖見圖2

5.3 Further Investigations of Proposed Method

由於本文篇幅所限，本文選擇了兩個資料集進行說明。其中一種是AS733，它包含了新增和刪除節點，而另一種是Elec，它只包含新增節點。

5.3.1 Necessity of Dynamic Network Embedding

動態網路嵌入的必要性對比見圖3

5.3.2 Incremental Learning vs Retraining

Dyn上的增量學習和重訓練對比見圖4

5.3.3 Visualization of Embeddings

嵌入穩定性對比見圖5

5.3.4 Different Node Selecting Strategies

從效能上來看 SGNS-increment>SGNS-retrain>SGNS-static

雖然SGNS-increment(即GloDyNE， α = 1.0)的效能最好，但它的效率不夠高，因為當前快照中的所有節點都被選擇來進行隨機遊走，然後訓練SGNS模型。

進一步提高效率的一個自然思路是選擇一些有代表性的節點作為近似解，這樣可以顯著減少遊走時間，同時仍然保持良好的效能。因此，在本文中，我們提出了節點選擇策略S4，如4.1.1節和4.1.2節所述

具體對比見表5

5.3.5 The Free Hyper-Parameter

超引數α決定每個時間步選擇的節點數，其設計可以在有效性和效率之間自由權衡。

對比見圖6

Summary

本文提出了考慮高階相似度對非活躍子網的影響，並皆由此保持全域性拓撲，還提出了劃分出各個子網之後，進行代表性節點的選擇，再去進行隨機遊走以減少時間消耗，但是效能損耗不大。這樣取樣的思路確實挺好的

論文閱讀 GloDyNE Global Topology Preserving Dynamic Network Embedding