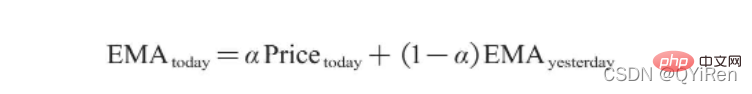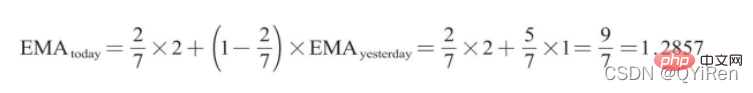Python隨機森林模型範例詳解

【相關推薦：Python3視訊教學 】

1 整合模型簡介

整合學習模型使用一系列弱學習器（也稱為基礎模型或基模型）進行學習，並將各個弱學習器的結果進行整合，從而獲得比單個學習器更好的學習效果。

整合學習模型的常見演演算法有Bagging演演算法和Boosting演演算法兩種。

Bagging演演算法的典型機器學習模型為隨機森林模型，而Boosting演演算法的典型機器學習模型則為AdaBoost、GBDT、XGBoost和LightGBM模型。

1.1 Bagging演演算法簡介

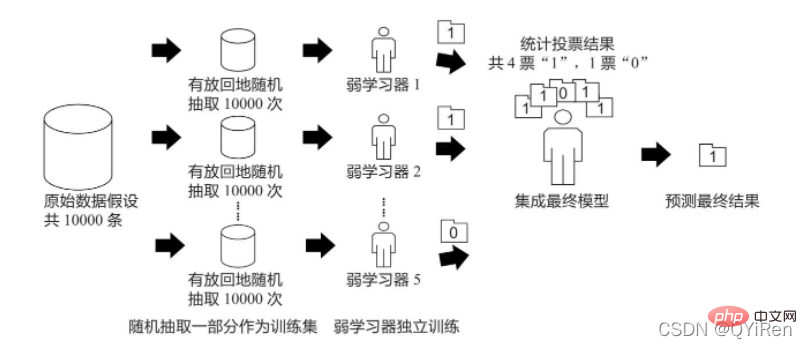
Bagging演演算法的原理類似投票，每個弱學習器都有一票，最終根據所有弱學習器的投票，按照「少數服從多數」的原則產生最終的預測結果，如下圖所示。

假設原始資料共有10000條，從中隨機有放回地抽取10000次資料構成一個新的訓練集（因為是隨機有放回抽樣，所以可能出現某一條資料多次被抽中，也有可能某一條資料一次也沒有被抽中），每次使用一個訓練集訓練一個弱學習器。這樣有放回地隨機抽取n次後，訓練結束時就能獲得由不同的訓練集訓練出的n個弱學習器，根據這n個弱學習器的預測結果，按照「少數服從多數」的原則，獲得一個更加準確、合理的最終預測結果。

具體來說，在分類問題中是用n個弱學習器投票的方式獲取最終結果，在迴歸問題中則是取n個弱學習器的平均值作為最終結果。

1.2 Boosting演演算法簡介

Boosting演演算法的本質是將弱學習器提升為強學習器，它和Bagging演演算法的區別在於：Bagging演演算法對待所有的弱學習器一視同仁；而Boosting演演算法則會對弱學習器「區別對待」，通俗來講就是注重「培養精英」和「重視錯誤」。

「培養精英」就是每一輪訓練後對預測結果較準確的弱學習器給予較大的權重，對錶現不好的弱學習器則降低其權重。這樣在最終預測時，「優秀模型」的權重是大的，相當於它可以投出多票，而「一般模型」只能投出一票或不能投票。

「重視錯誤」就是在每一輪訓練後改變訓練集的權值或概率分佈，通過提高在前一輪被弱學習器預測錯誤的樣例的權值，降低前一輪被弱學習器預測正確的樣例的權值，來提高弱學習器對預測錯誤的資料的重視程度，從而提升模型的整體預測效果。

2 隨機森林模型基本原理

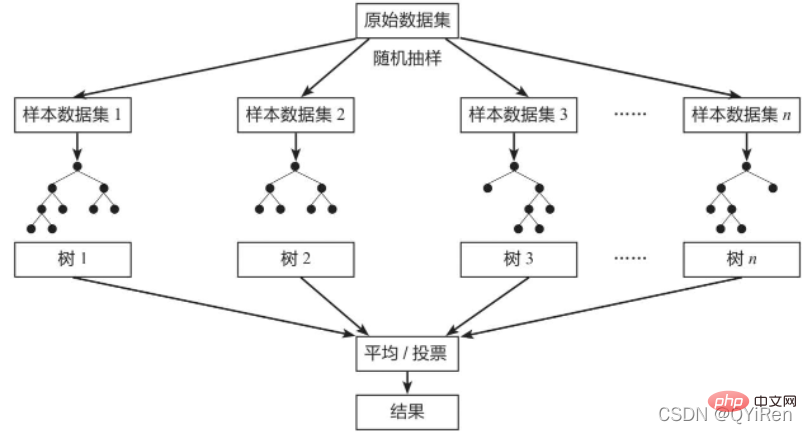
隨機森林（Random Forest）是一種經典的Bagging模型，其弱學習器為決策樹模型。如下圖所示，隨機森林模型會在原始資料集中隨機抽樣，構成n個不同的樣本資料集，然後根據這些資料集搭建n個不同的決策樹模型，最後根據這些決策樹模型的平均值（針對迴歸模型）或者投票情況（針對分類模型）來獲取最終結果。

為了保證模型的泛化能力（或者說通用能力），隨機森林模型在建立每棵樹時，往往會遵循「資料隨機」和「特徵隨機」這兩個基本原則。

資料隨機：從所有資料當中有放回地隨機抽取資料作為其中一個決策樹模型的訓練資料。例如，有1000個原始資料，有放回地抽取1000次，構成一組新的資料，用於訓練某一個決策樹模型。

特徵隨機：如果每個樣本的特徵維度為M，指定一個常數k＜M，隨機地從M個特徵中選取k個特徵。

與單獨的決策樹模型相比，隨機森林模型由於整合了多個決策樹，其預測結果會更準確，且不容易造成過擬合現象，泛化能力更強。

3 使用sklearn實現隨機森林模型

隨機森林模型既能進行分類分析，又能進行迴歸分析，對應的模型分別為：

·隨機森林分類模型（RandomForestClassifier）

·隨機森林迴歸模型（RandomForestRegressor）

隨機森林分類模型的弱學習器是分類決策樹模型，隨機森林迴歸模型的弱學習器則是迴歸決策樹模型。

程式碼如下。

from sklearn.ensemble import RandomForestClassifier
X = [[1,2],[3,4],[5,6],[7,8],[9,10]]
y = [0,0,0,1,1]

# 設定弱學習器數量為10
model = RandomForestClassifier(n_estimators=10,random_state=123)
model.fit(X,y)

model.predict([[5,5]])

# 輸出為：array([0])

4 案例：股票漲跌預測模型

4.1 股票衍生變數生成

本節講解如何利用股票的基本資料獲取一些衍生變數資料，如股票技術分析常用的均線指標5日均線價格MA5與10日均線價格MA10、相對強弱指標RSI、動量指標MOM、指數移動平均值EMA、異同移動平均線MACD等。

4.1.1 獲取股票基本資料

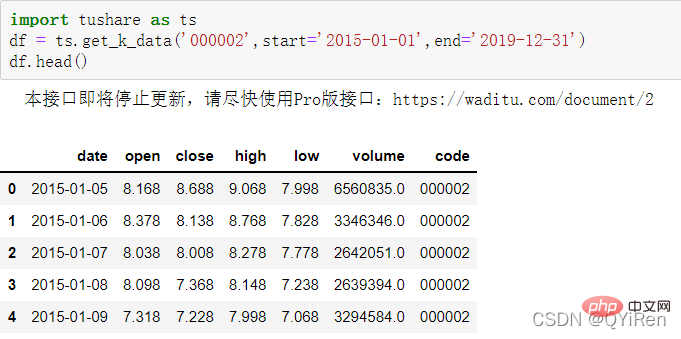
首先用get_k_data()函數獲取2015-01-01到2019-12-31的股票基本資料，程式碼如下。

前5行資料如下圖所示，其中缺失的資料為節假日（非交易日）資料。

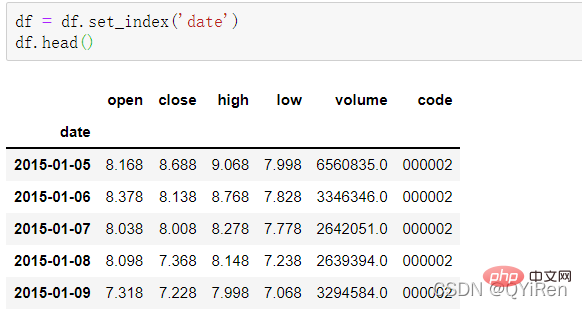
用set_index()函數將date列設定為行索引，程式碼如下。

4.1.2 生成簡單衍生變數

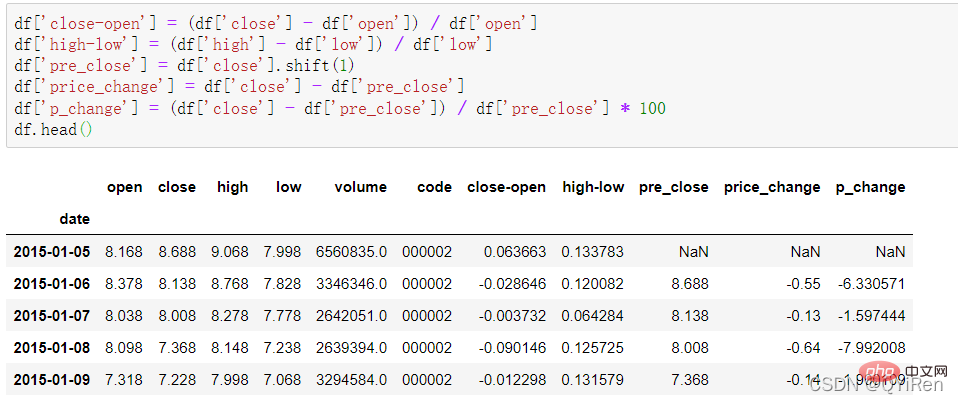
通過如下程式碼可以生成一些簡單的衍生變數資料。

close-open表示（收盤價-開盤價）/開盤價；

high-low表示（最高價-最低價）/最低價；

pre_close表示昨日收盤價，用shift（1）將close列的所有資料向下移動1行並形成新的1列，如果是shift（-1）則表示向上移動1行；

price_change表示今日收盤價-昨日收盤價，即當天的股價變化；

p_change表示當天股價變化的百分比，也稱為當天股價的漲跌幅。

4.1.3 生成移動平均線指標MA值

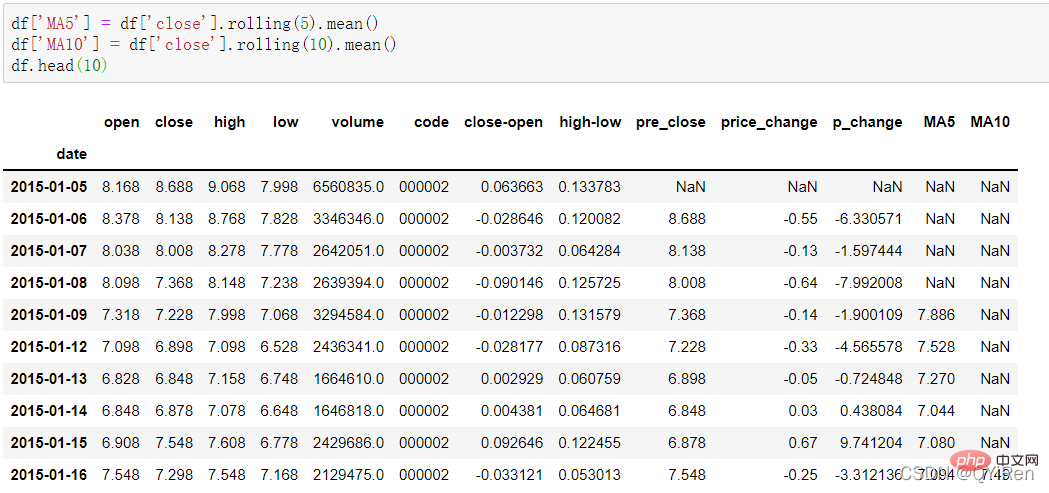
通過如下程式碼可以生成股價的5日移動平均值和10日移動平均值。

注意：rolling函數的使用

其中，MA是移動平均線的意思，「平均」是指最近n天收盤的算術平均值，「移動」是指在計算中始終採用最近n天的價格資料。

例如：MA5的計算

根據上述資料，5號的MA5值為（1.2＋1.4＋1.6＋1.8＋2.0）/5＝1.6，而6號的MA5值則為（1.4＋1.6＋1.8＋2.0＋2.2）/5＝1.8，依此類推。將一段時期內股價的移動平均值連成曲線，即為移動平均線。同理，MA10為從計算當天起前10天的股價平均值。

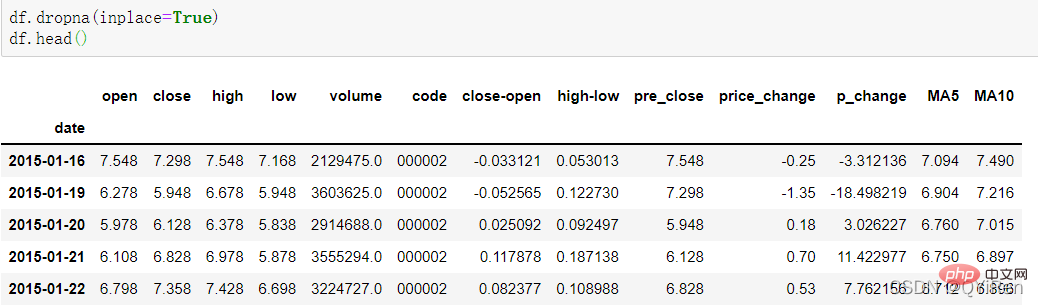
在計算像MA5這樣的資料時，因為最開始的4天資料量不夠，這4天對應的移動平均值是無法計算出來的，所以會產生空值NaN。通常會用dropna()函數刪除空值，以免在後續計算中出現因空值造成的問題，程式碼如下。

可以看到16號以前的行被刪除。

4.1.4 用TA-Lib庫生成相對強弱指標RSI值

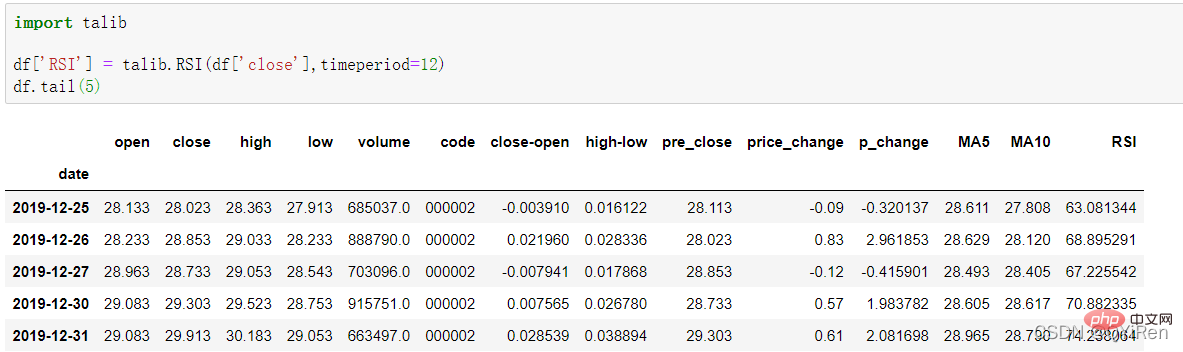
通過如下程式碼可以生成相對強弱指標RSI值。

RSI值能反映短期內股價漲勢相對於跌勢的強弱，幫助我們更好地判斷股價的漲跌趨勢。

RSI值越大，漲勢相對於跌勢越強，反之則漲勢相對於跌勢越弱。

RSI值的計算公式如下。

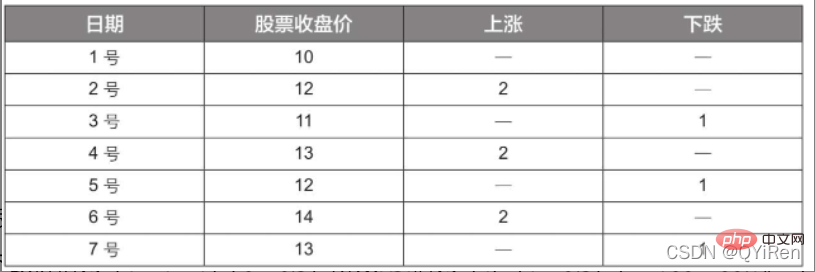
舉例：

根據上表資料，取N＝6，可求得6日平均上漲價格為（2＋2＋2）/6＝1，6日平均下跌價格為（1＋1＋1）/6＝0.5，所以RSI值為（1/（1＋0.5））×100＝66.7。

通常情況下，RSI值位於20～80之間，超過80則為超買狀態，低於20則為超賣狀態，等於50則認為買賣雙方力量均等。例如，如果連續6天股價都是上漲，則6日平均下跌價格為0，6日RSI值為100，表明此時股票買方處於非常強勢的地位，但也提醒投資者要警惕此時可能也是超買狀態，需要預防股價下跌的風險。

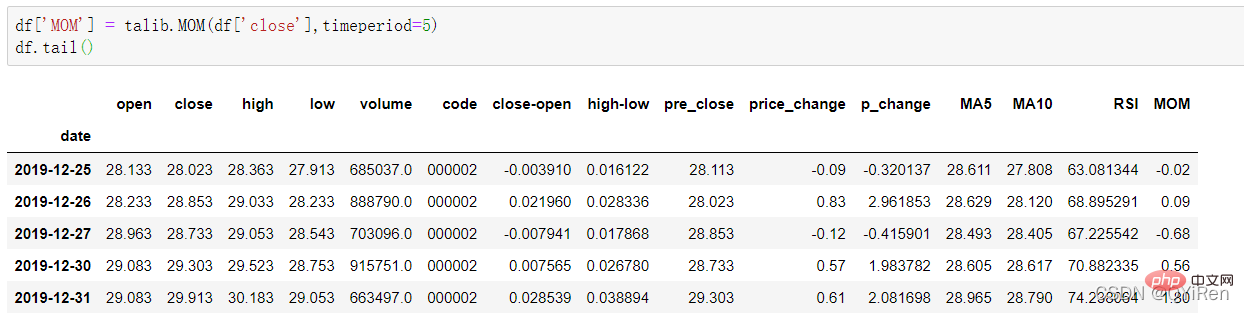
4.1.5 用TA-Lib庫生成動量指標MOM值

通過如下程式碼可以生成動量指標MOM值。

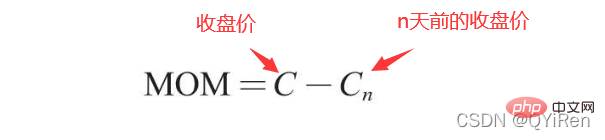
MOM是momentum（動量）的縮寫，它反映了一段時期內股價的漲跌速度，計算公式如下。

舉例：

假設要計算6號的MOM值，而前面的程式碼中設定引數timeperiod為5，那麼就需要用6號的收盤價減去1號的收盤價，即6號的MOM值為2.2-1.2＝1，同理，7號的MOM值為2.4-1.4＝1。將連續幾天的MOM值連起來就構成一條反映股價漲跌變動的曲線。

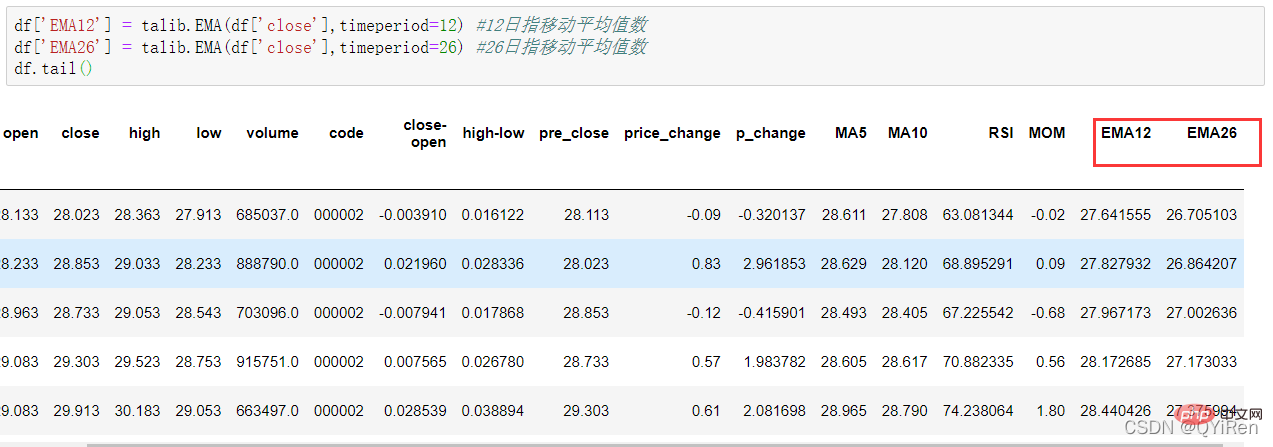
4.1.6 用TA-Lib庫生成指數移動平均值EMA

通過如下程式碼可以生成指數移動平均值EMA。

EMA是以指數式遞減加權的移動平均，並根據計算結果進行分析，用於判斷股價未來走勢的變動趨勢。

EMA的計算公式如下。

其中，EMAtoday為當天的EMA值；Pricetoday為當天的收盤價；EMAyesterday為昨天的EMA值；α為平滑指數，一般取值為2/（N＋1），N表示天數，當N為6時，α為2/7，對應的EMA稱為EMA6，即6日指數移動平均值。公式不斷遞迴，直至第1個EMA值出現（第1個EMA值通常為開頭5個數的均值）。

舉例：EMA6

取第1個EMA值為開頭5個數的均值，故前5天都沒有EMA值；6號的EMA值就是第1個EMA值，為前5天的均值，即1；7號的EMA值為第2個EMA值，計算過程如下。

4.1.7 用TA-Lib庫生成異同移動平均線MACD值

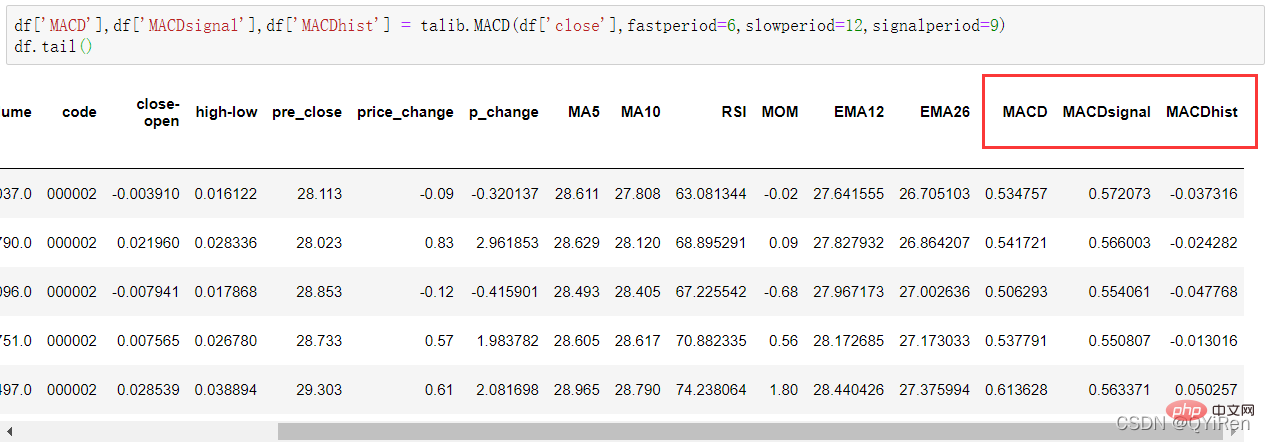
通過如下程式碼可以生成異同移動平均線MACD值。

MACD是股票市場上的常用指標，它是基於EMA值的衍生變數，計算方法比較複雜，感興趣的讀者可以自行了解。這裡只需要知道MACD是一種趨勢類指標，其變化代表著市場趨勢的變化，不同K線級別的MACD代表當前級別週期中的買賣趨勢。

4.2 模型搭建

4.2.1 引入需要搭建的庫

# 匯入相關庫
import tushare as ts
import numpy as np
import pandas as pd
import talib
import matplotlib.pyplot as plt
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import accuracy_score

4.2.2 獲取資料

# 1.股票基本資料獲取
import tushare as ts
df = ts.get_k_data('000002',start='2015-01-01',end='2019-12-31')
df = df.set_index('date')

# 2.簡單衍生變數資料構造
df['close-open'] = (df['close'] - df['open']) / df['open']
df['high-low'] = (df['high'] - df['low']) / df['low']
df['pre_close'] = df['close'].shift(1)
df['price_change'] = df['close'] - df['pre_close']
df['p_change'] = (df['close'] - df['pre_close']) / df['pre_close'] * 100

# 3.移動平均線相關資料構造
df['MA5'] = df['close'].rolling(5).mean()
df['MA10'] = df['close'].rolling(10).mean()
df.dropna(inplace=True)

# 4.通過TA-Lib庫構造衍生變數資料
df['RSI'] = talib.RSI(df['close'],timeperiod=12)
df['MOM'] = talib.MOM(df['close'],timeperiod=5)
df['EMA12'] = talib.EMA(df['close'],timeperiod=12) #12日指移動平均值數
df['EMA26'] = talib.EMA(df['close'],timeperiod=26) #26日指移動平均值數
df['MACD'],df['MACDsignal'],df['MACDhist'] = talib.MACD(df['close'],fastperiod=6,slowperiod=12,signalperiod=9)
df.dropna(inplace=True)

4.2.3 提取特徵變數和目標變數

X = df[['close','volume','close-open','MA5','MA10','high-low','RSI','MOM','EMA12','MACD','MACDsignal','MACDhist']]
y = np.where(df['price_change'].shift(-1) > 0,1,-1)

首先強調最核心的一點：應該是用當天的股價資料預測下一天的股價漲跌情況，所以目標變數y應該是下一天的股價漲跌情況。為什麼是用當天的股價資料預測下一天的股價漲跌情況呢？這是因為特徵變數中的很多資料只有在當天交易結束後才能確定（例如，收盤價close只有收盤了才有），所以當天正在交易時的股價漲跌情況是無法預測的，而等到收盤時儘管所需資料齊備，但是當天的股價漲跌情況已成定局，也就沒有必要預測了，所以是用當天的股價資料預測下一天的股價漲跌情況。

第2行程式碼中使用了NumPy庫中的where()函數，傳入的3個引數的含義分別為判斷條件、滿足條件的賦值、不滿足條件的賦值。其中df['price_change'].shift（-1）是利用shift()函數將price_change（股價變化）這一列的所有資料向上移動1行，這樣就獲得了每一行對應的下一天的股價變化。因此，這裡的判斷條件就是下一天的股價變化是否大於0，如果大於0，說明下一天股價漲了，則y賦值為1；如果不大於0，說明下一天股價不變或跌了，則y賦值為-1。預測結果就只有1或-1兩種分類。

4.2.4 劃分訓練集和測試集

這裡需要注意的是，劃分要按照時間序列進行，而不能用train_test_split()函數進行隨機劃分。這是因為股價的變化趨勢具有時間性特徵，而隨機劃分會破壞這種特徵，所以需要根據當天的股價資料預測下一天的股價漲跌情況，而不能根據任意一天的股價資料預測下一天的股價漲跌情況。

將前90%的資料作為訓練集，後10%的資料作為測試集，程式碼如下。

X_length = X.shape[0]
split = int(X_length * 0.9)
X_train,X_test = X[:split],X[split:]
y_train,y_test = y[:split],y[split:]

4.2.5 模型搭建

model = RandomForestClassifier(max_depth=3,n_estimators=10,min_samples_leaf=10,random_state=123)
model.fit(X_train,y_train)

設定模型引數：決策樹的最大深度max_depth設定為3，即每個決策樹最多隻有3層；弱學習器（即決策樹模型）的個數n_estimators設定為10，即該隨機森林中共有10個決策樹；葉子節點的最小樣本數min_samples_leaf設定為10，即如果葉子節點的樣本數小於10則停止分裂；隨機狀態引數random_state的作用是使每次執行結果保持一致，這裡設定的數位123沒有特殊含義，可以換成其他數位。

4.3 模型評估與使用

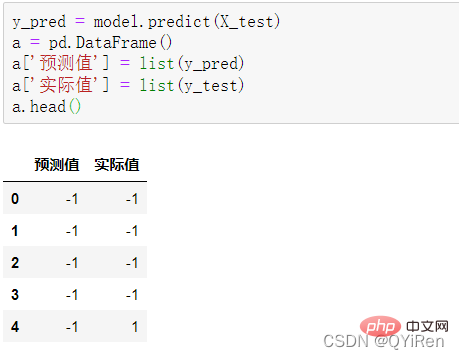
4.3.1 預測下一天的股價漲跌情況

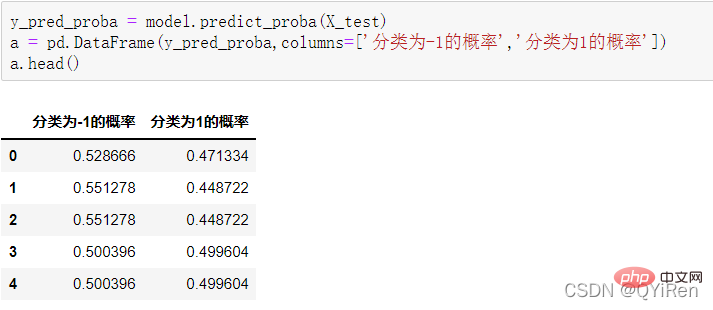
用predict_proba()函數可以預測屬於各個分類的概率，程式碼如下。

4.3.2 模型準確度評估

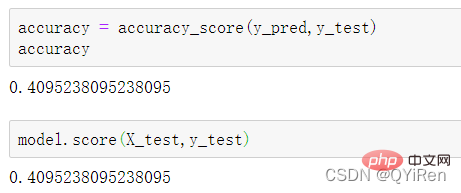
通過如下程式碼可以檢視整體的預測準確度。

列印輸出score為0.40，說明模型對整個測試集中約40%的資料預測正確。這一預測準確度並不算高，也的確符合股票市場千變萬化的特點。

4.3.3 分析特徵變數的特徵重要性

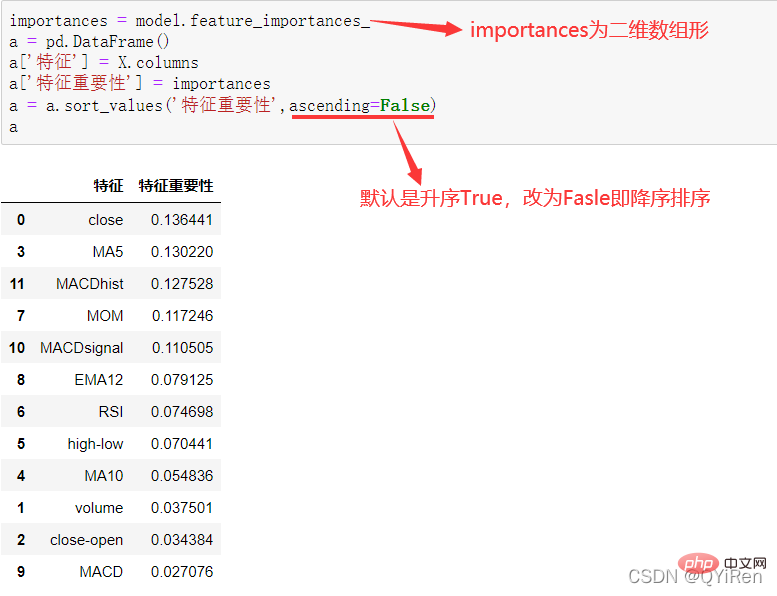
通過如下程式碼可以分析各個特徵變數的特徵重要性。

由圖可知，當日收盤價close、MA5、MACDhist相關指標等特徵變數對下一天股價漲跌結果的預測準確度影響較大。

4.4 引數調優

from sklearn.model_selection import GridSearchCV
parameters={'n_estimators':[5,10,20],'max_depth':[2,3,4,5,6],'min_samples_leaf':[5,10,20,30]}
new_model = RandomForestClassifier(random_state=123)
grid_search = GridSearchCV(new_model,parameters,cv=6,scoring='accuracy')
grid_search.fit(X_train,y_train)
grid_search.best_params_

# 輸出
# {'max_depth': 5, 'min_samples_leaf': 20, 'n_estimators': 5}

4.5 收益回測曲線繪製

前面已經評估了模型的預測準確度，不過在商業實戰中，更關心它的收益回測曲線（又稱為淨值曲線），也就是看根據搭建的模型獲得的結果是否比不利用模型獲得的結果更好。

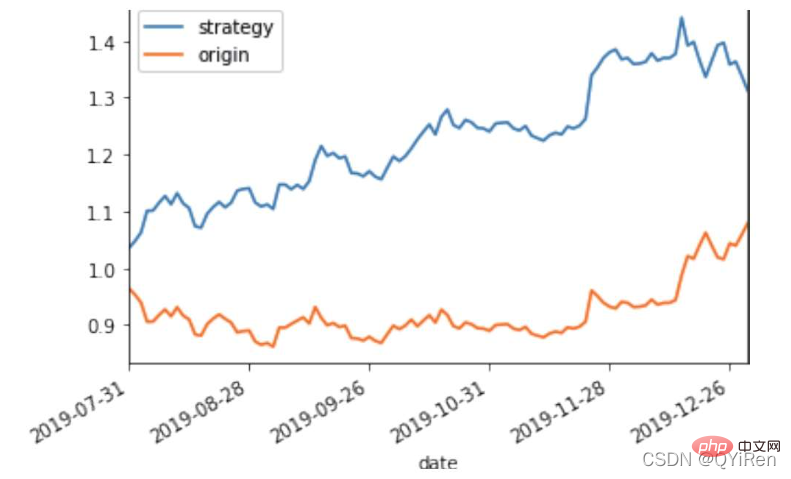
# 在測試資料上新增一列，預測收益
X_test['prediction'] = model.predict(X_test)

# 計算每天的股價變化率
X_test['p_change'] = (X_test['close'] - X_test['close'].shift(1)) / X_test['close'].shift(1)

# 計算累積收益率
# 例如，初始股價是1，2天內的價格變化率為10%
# 那麼用cumprod()函數可以求得2天后的股價為1×（1＋10%）×（1＋10%）＝1.21
# 此結果也表明2天的收益率為21%。
X_test['origin'] = (X_test['p_change'] + 1).cumprod()

# 計算利用模型預測後的收益率
X_test['strategy'] = (X_test['prediction'].shift(1) * X_test['p_change'] + 1).cumprod()

X_test[['strategy','origin']].dropna().plot()
# 設定自動傾斜
plt.gcf().autofmt_xdate()
plt.show()

視覺化結果如下圖所示。圖中上方的曲線為根據模型得到的收益率曲線，下方的曲線為股票本身的收益率曲線，可以看到，利用模型得到的收益還是不錯的。

要說明的是，這裡講解的量化金融內容比較淺顯，搭建的模型過於理想化，真正的股市是錯綜複雜的，股票交易也有很多限制，如不能做空、不能T＋0交易，還要考慮手續費等因素。

隨機森林模型是一種非常重要的整合模型，它整合了決策樹模型的眾多優點，又規避了決策樹模型容易過度擬合等缺點，在實戰中應用較為廣泛。

【相關推薦：Python3視訊教學 】

以上就是Python隨機森林模型範例詳解的詳細內容，更多請關注TW511.COM其它相關文章！