【機器學習】K-means聚類分析
2022-06-30 18:16:46
前言
聚類問題是無監督學習的問題,演演算法思想就是物以類聚,人以群分,聚類演演算法感知樣本間的相似度,進行類別歸納,對新輸入進行輸出預測,輸出變數取有限個離散值。本次我們使用兩種方法對鳶尾花資料進行聚類。
- 無監督就是沒有標籤的進行分類
K-means 聚類演演算法
K-means聚類演演算法(k-均值或k-平均)聚類演演算法。演演算法思想就是首先隨機確定k箇中心點作為聚類中心,然後把每個資料點分配給最鄰近的中心點,分配完成後形成k個聚類,計算各個聚類的平均中心點,將其作為該聚類新的類中心點,然後迭代上述步驟知道分配過程不在產生變化。
演演算法流程
- 隨機選擇K個隨機點(成為聚類中心)
- 對資料集中的每個資料點,按照距離K箇中心點的距離,將其與距離最近的中心點關聯起來,與同一中心點關聯的所有點聚成一類
- 計算每一組的均值,將改組所關聯的中心點移動到平均值位置
- 重複上兩步,直至中心點不再發生變化
優缺點
優點:
- 原理比較簡單,實現容易,收斂速度快
- 聚類效果比較優
- 演演算法可解釋度比較強
- 主要需要調參的引數僅僅是簇數K
缺點:
- K值選取不好把握
- 不平衡資料集聚類效果不佳
- 採用迭代方法,得到結果只是區域性最優
- 對噪音和異常點比較敏感
鳶尾花聚類
資料集
資料集:資料集採用sklern中的資料集
資料集分佈圖:我們可以看出資料的大致分佈情況
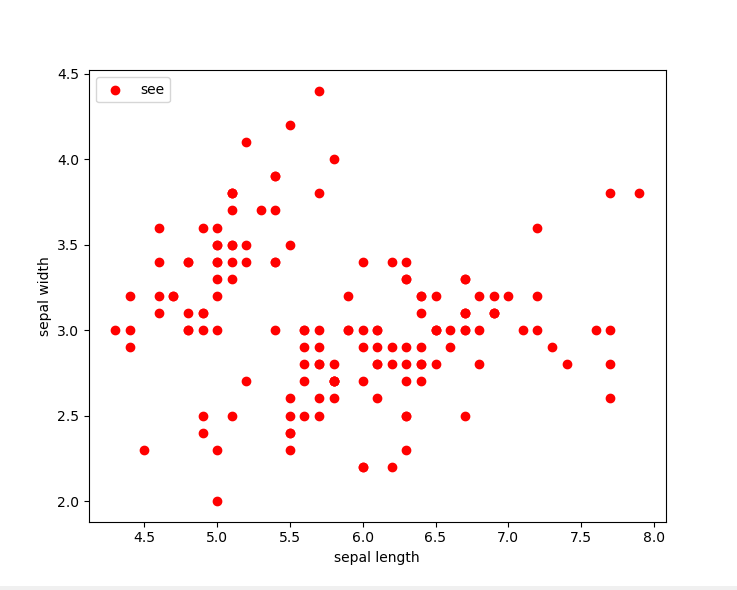
使用sklearn中的模型
# 鳶尾花資料集 150 條資料
## 導包
import numpy as np
import matplotlib.pyplot as plt
# 匯入資料集包
from sklearn import datasets
from sklearn.cluster import KMeans
## 載入資料據集
iris = datasets.load_iris()
X = iris.data[:,:4]
print(X.shape) # 150*4
## 繪製二維資料分佈圖
## 前兩個特徵
plt.scatter(X[:,0],X[:,1],c='red',marker='o',label='see')
plt.xlabel('sepal length')
plt.ylabel('sepal width')
plt.legend(loc=2)
plt.show()
'''
直接呼叫包
'''
## 範例化K-means類,並定義訓練函數
def Model(n_clusters):
estimator = KMeans(n_clusters=n_clusters)
return estimator
## 定義訓練韓碩
def train(estimator):
estimator.fit(X)
## 訓練
estimator = Model(3)
## 開啟訓練擬合
train(estimator=estimator)
## 視覺化展示
label_pred = estimator.labels_ # 獲取聚類標籤
## 找到3中聚類結構
x0 = X[label_pred==0]
x1 = X[label_pred==1]
x2 = X[label_pred==2]
plt.scatter(x0[:,0],x0[:,1],c='red',marker='o',label='label0')
plt.scatter(x1[:,0],x1[:,1],c='green',marker='*',label='label1')
plt.scatter(x2[:,0],x2[:,1],c='blue',marker='+',label='label2')
plt.xlabel('sepal length')
plt.ylabel('sepal width')
plt.legend(loc=2)
plt.show()
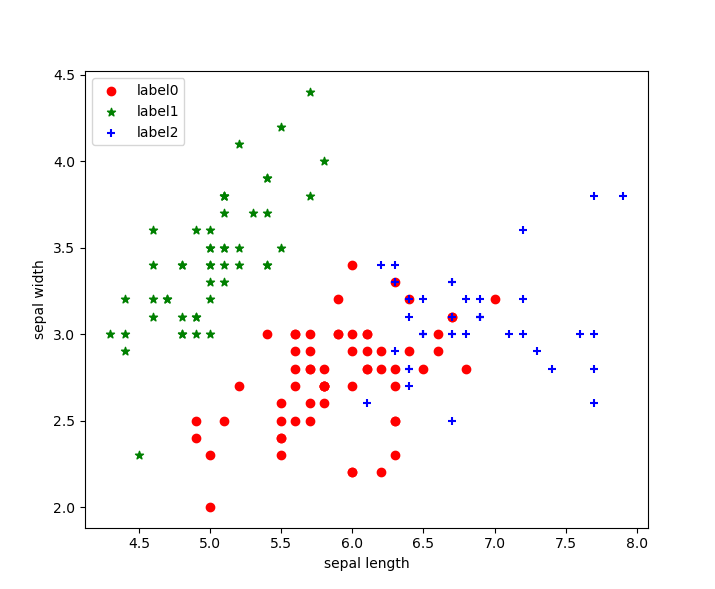
聚類結果
我們可以看出聚類結果按照我們的要求分為了三類,分別使用紅、藍、綠三種顏色進行了展示!
聚類效果圖:
手寫K-means演演算法
# 鳶尾花資料集 150 條資料
## 導包
import numpy as np
import matplotlib.pyplot as plt
# 匯入資料集包
from sklearn import datasets
from sklearn.cluster import KMeans
## 載入資料據集
iris = datasets.load_iris()
X = iris.data[:,:4]
print(X.shape) # 150*4
## 繪製二維資料分佈圖
## 前兩個特徵
plt.scatter(X[:,0],X[:,1],c='red',marker='o',label='see')
plt.xlabel('sepal length')
plt.ylabel('sepal width')
plt.legend(loc=2)
plt.show()
'''
直接手寫實現
'''
'''
1、隨機初始化 隨機尋找k個簇的中心
2、對這k箇中心進行聚類
3、重複1、2,知道中心達到穩定
'''
### 歐氏距離計算
def distEclud(x,y):
return np.sqrt(np.sum((x-y)**2))
### 為資料集定義簇的中心
def randCent(dataSet,k):
m,n = dataSet.shape
centroids = np.zeros((k,n))
for i in range(k):
index = int(np.random.uniform(0,m))
centroids[i,:] = dataSet[index,:]
return centroids
## k均值聚類演演算法
def KMeans(dataSet,k):
m = np.shape(dataSet)[0]
clusterAssment = np.mat(np.zeros((m,2)))
clusterChange = True
## 1 初始化質心centroids
centroids = randCent(dataSet,k)
while clusterChange:
# 樣本所屬簇不在更新時停止迭代
clusterChange = False
# 遍歷所有樣本
for i in range(m):
minDist = 100000.0
minIndex = -1
# 遍歷所有質心
# 2 找出最近質心
for j in range(k):
distance = distEclud(centroids[j,:],dataSet[i,:])
if distance<minDist:
minDist = distance
minIndex = j
# 更新該行所屬的簇
if clusterAssment[i,0] != minIndex:
clusterChange = True
clusterAssment[i,:] = minIndex,minDist**2
# 更新質心
for j in range(k):
pointsInCluster = dataSet[np.nonzero(clusterAssment[:,0].A == j)[0]] # 獲取對應簇類所有的點
centroids[j,:] = np.mean(pointsInCluster,axis=0)
print("cluster complete")
return centroids,clusterAssment
def draw(data, center, assment):
length = len(center)
fig = plt.figure
data1 = data[np.nonzero(assment[:,0].A == 0)[0]]
data2 = data[np.nonzero(assment[:,0].A == 1)[0]]
data3 = data[np.nonzero(assment[:,0].A == 2)[0]]
# 選取前兩個資料繪製原始資料的散點
plt.scatter(data1[:,0],data1[:,1],c='red',marker='o',label='label0')
plt.scatter(data2[:,0],data2[:,1],c='green',marker='*',label='label1')
plt.scatter(data3[:,0],data3[:,1],c='blue',marker='+',label='label2')
# 繪製簇的質心點
for i in range(length):
plt.annotate('center',xy=(center[i,0],center[i,1]),xytext=(center[i,0]+1,center[i,1]+1),arrowprops=dict(facecolor='yellow'))
plt.show()
# 選取後兩個維度繪製原始資料散點圖
plt.scatter(data1[:, 2], data1[:, 3], c='red', marker='o', label='label0')
plt.scatter(data2[:, 2], data2[:, 3], c='green', marker='*', label='label1')
plt.scatter(data3[:, 2], data3[:, 3], c='blue', marker='+', label='label2')
# 繪製簇的質心點
for i in range(length):
plt.annotate('center', xy=(center[i, 2], center[i, 3]), xytext=(center[i, 2] + 1, center[i, 3] + 1),
arrowprops=dict(facecolor='yellow'))
plt.show()
## 呼叫
dataSet = X
k = 3
centroids,clusterAssment = KMeans(dataSet,k)
draw(dataSet,centroids,clusterAssment)
效果圖展示
我們可以看到手寫實現的也通過三種顏色實現類,可以看出兩種方式實現結果是幾乎相同的。
-
根據花萼長度花萼寬度聚類
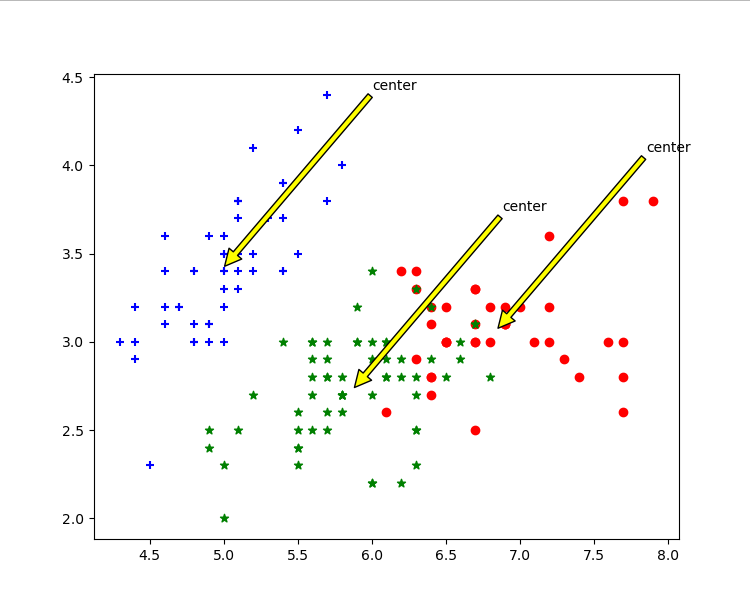
-
根據花瓣長度花瓣寬度聚類:
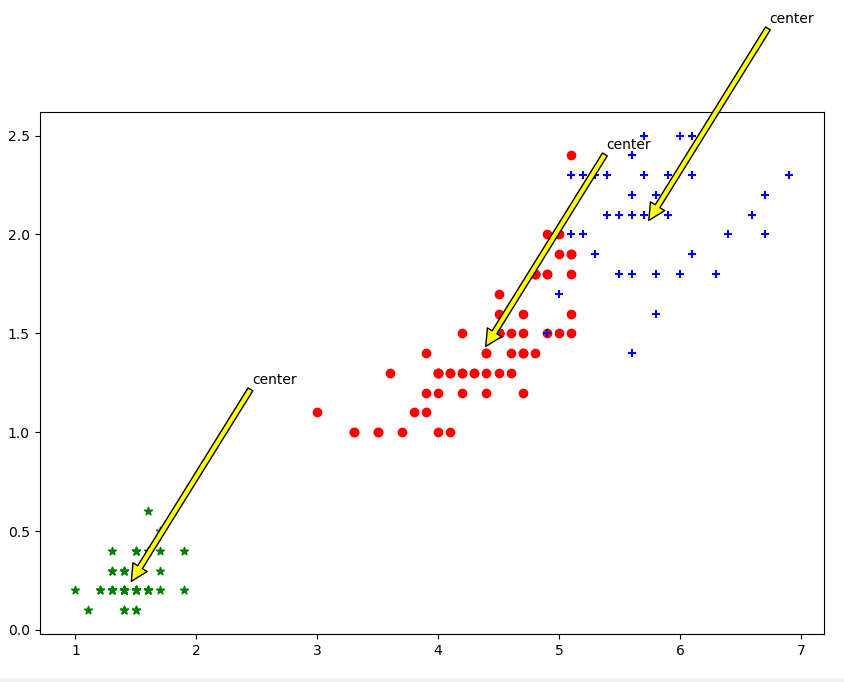
總結
我們既可以使用sklearn包中封裝好的模型進行聚類分析,也可以自己手寫實現,在某些問題上,兩者都可以達到相同的結果,我們對於不同的問題可以更合適的方法進行處理。