Multiparty Cardinality Testing for Threshold Private Set-2021：解讀

本文記錄閱讀該論文的筆記。

本文基於閾值加法同態加密方案提出了一個新的允許$N$方檢查其輸入集的交集是否大於$n-t$的IPSI方案，該協定的通訊複雜度為$O(Nt^2)$。
注意：$N$指的是多少個參與方、$n$是輸入集的大小、$t$是預先設定的閾值，也是閾值。

該方案基於The Communication Complexity of Threshold Private Set Intersection-2019：解讀進行的改進。
該協定可以用於各方知道交集很大，但不知道具體多大時，可以使用！

摘要

（1）該協定的通訊複雜度不依賴於輸入集的大小，而取決於閾值$t$的大小
（2）基於閾值的PSI協定分為兩部分：

交集的勢測試（Cardinality Testing ），即測試參與方的交集是否大於$n-t$
PSI：計算交集

介紹

兩方閾值PSI：

（1）雙方先檢測交集大小是否$> n-t$
（2）若滿足，則求交（獲取交集）；否則，什麼也得不到（獲取不到交集）

標準PSI和閾值PSI的對比：

標準的PSI更在乎交集，而不在乎交集的大小，而閾值PSI更關注交集的大小。
閾值PSI的通訊量較少，只取決於閾值$t$的大小；標準的PSI通訊量取決於輸入集合的大小。

閾值PSI現狀：
只有以下方案進行了討論：
（1）【Privatepool: Privacy-preserving ridesharing-2017】
（2）【An algebraic approach to maliciously secure private set intersection-2019】
（3）【The communication complexity of threshold private set intersection-2019】
其中只有（3）的通訊複雜度不依賴於$n$，方案是兩方場景。
（4）【Multi-party threshold private set intersection with sublinear communication-2021】
這也是一個多方閾值PSI，使用FHE，通訊複雜度為$O(Nt)$，也提出了一個TPKE加密方案實現了：只有當各方的交集足夠大時，各方才能求交集。還可以祕密的計算漢克爾矩陣的行列式（矩陣大小的線性時間內）。

閾值PSI的應用：
（1）約會APP
（2）生物特徵認證
（3）拼車【Privatepool: Privacy-preserving ridesharing 】
假設兩個（或更多）方正在使用拼車應用程式，如果他們的路線有很大的交集，它允許他們共用車輛。然而由於隱私問題，他們不想公開他們的行程。閾值PSI可以解決該問題，各方可以聯合執行一個閾值PSI協定，瞭解路線的交叉點，如果交叉點足夠大，共用一輛車，否則，他們就不共用一輛車，也能保證使用者的路線隱私。

閾值PSI

當前的閾值PSI主要分為兩步：
（1）Cardinality Testing：就是各方檢測交集是否大於$n-t$
（2）PSI：如果滿足（1），則輸出交集；否則沒有輸出

具體：

如果起始$t=1$，則$t$的取值範圍有：$1,2,4,8,...,t,2t$

通訊複雜只取決於$t$的原因：

合適的閾值一定是2的次冪，如果交集大於$n-t'$，則Cardinality Testing對於閾值$t$就成功，因為$t\geq t'>t/2$，所以協定的通訊複雜度只取決於閾值的大小。

解釋有點牽強，或許我沒理解
$t'$是什麼？

貢獻

（1）多方Cardinality Testing

較上面的Cardinality Testing，這裡給出了滿足多方的Cardinality Testing
通訊複雜度為$O(Nt^2)$
並給出一些新的線性計算（linear algebra）：求密文矩陣相乘、求密文矩陣的秩、求密文矩陣的逆等

該協定在【Secure linear algebra using linearly recurrent sequences-2007】【Communication eﬃcient secure linear algebra-2006】的（兩方）基礎上構建的多方閾值PSI。

（2）多方閾值PSI

這裡也是將一個兩方的協定改為多方。

回顧一下兩方的情況：
兩方Alice和Bob各有資料$S_A$和$S_B$，其大小都是$n$，閾值$t<<n$，如果$|S_A\cap S_B|\geq n-t$，則求出交集$S_A\cap S_B$。

我們方案基於【The communication complexity of threshold private set intersection-2019】論文，這是一個兩方的閾值PSI協定：

（1）若交集大於$n-t$
（2）計算交集
兩方將資料編碼到多項式中，得到$P_A(x)=(x-a_i)...(x-a_n)$和$P_B=(x-b_1)...(x-b_n)$在一個大的有限域上$F$，其中$a_i\in S_A,b_i\in S_B$，然後只要滿足$|S_A\cap S_B|\geq n-t$，則：

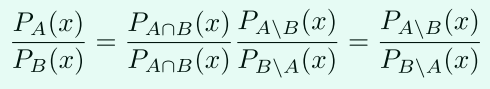
且$deg(P_A)=deg(P_B)=t$，所以兩方只需要在$P_A(x)/P_B(x)=P_{A\setminus B}(x)/P_{B\setminus A}$上計算$O(t)$個點。然後將這些點插值得到$P_A(x)/P_B(x)$，然後求出分母$P_{B\setminus A}$，繼而求出交集多項式$P_{A\setminus B}(x)=P_B(x)/P_{B\setminus A}$

緊接上文問題：具體如何根據$P_A(x)/P_B(x)$，然後求出分母$P_{B\setminus A}$？

Bob不能恢復出分子$P_{A\setminus B}$，否則方案就不安全了，所以這裡使用Oblivious Linear Evaluation (OLE)技術用於「掩蓋」分子項（隨機化）。

該協定只有滿足$|S_A\cap S_B|\geq n-t$，才是安全的，否則就會洩露額外的資訊，所以雙方應該先執行Cardinality Testing操作，來保證協定是滿足$|S_A\cap S_B|\geq n-t$的。

擴充套件到多方的限制：

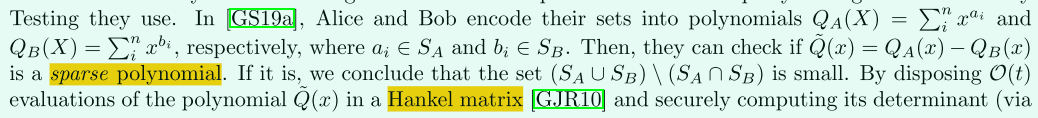
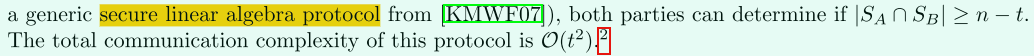
這裡講的是Cardinality Testing如何擴充套件為多方：

參與方先將資料編碼到多項式中，得到$Q_A(x)=x^{a_i}+...+x^{a_n}$和$Q_B=x^{b_1}+...+x^{b_n}$，其中$a_i\in S_A,b_i\in S_B$，檢測$Q(x)=Q_A(x)-Q_B(x)$是否是一個稀疏多項式（sparse polynomial），若是，則判斷集合$(S_A \cup S_B)\setminus (S_A \cap S_B)$是小集合（small），通訊複雜度為$O(t^2)$。
那問題來了：
（1）如何判斷多項式是否時稀疏的？
（2）如何判斷集合是小的？

如果將其擴充套件為多方，對於$N$個參與者，有：$\widetilde{Q}(x)=(N-1)Q_1(x)-Q_2(x)-...-Q_N(x)$，如果$N$很小的話，那該多項式$\widetilde{Q}(x)$就是稀疏的，那我們要是能計算該多項式的稀疏性，那麼Cardinality Testing協定的總通訊量變為$O((Nt)^2)$。

主要方法

1、安全線性代數（Secure Linear Algebra ）
來源【Secure linear algebra using linearly recurrent sequences 】
有兩個參與方，一方有矩陣的加密$Enc(pk,M)$，另一方有對應的解密私鑰$sk$，他們想要對這個密文矩陣做運算（線性計算，linear algebra related ），比如：求逆矩陣的行列式、秩或者計算出$x$，對於$Mx=y$，給出加密的$M,y$。

我們可以將該問題擴充套件到方，對於N個參與者$P_1,...,P_N$，每人有一份私鑰的分享值，此外$P_1$有一個加密的矩陣，目的是要對這個加密的矩陣做運算（線性計算，linear algebra related）。

我們發現可以將【secure linear algebra】協定擴充套件為多方場景，通過使用具有加法同態性的閾值PKE代替具有加法同態的PKE和GC代替來實現，所以該方案允許N方在閾值PKE下解決這個線性代數問題$Mx=y$。

2、多方勢檢測（Cardinality Testing via Degree Test of a Rational Function ）
對於參與方編碼的多項式$P_{S_i}(x)=(x-a_1^{(i)})...(x-a_n^{(i)}),i\in [1, N]$，有：

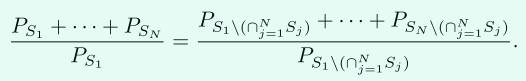
若交集$\cap S_i$大小大於$n-t$，則$deg(P_{S_1\setminus (\cap S_i)})=...=deg(P_{S_N\setminus (\cap S_i)})\leq t$。

以上是求交的方法！

所以Cardinality Testing有以下問題：
對於有理函數$f(x)=P_1(x)/P_2(x)$，能否安全的判斷$deg(P_1(x))=deg(P_2(x))\leq t$，進而通過插值$O(t)$個點得到$f(x)$？

我們發現，將$V=(v_i,f(v_i))$和$W=(w_i,f(w_i))$($2t$個點值)，插值為多項式$f_V(x),f_W(x)$，滿足：

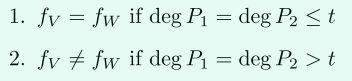
另外，插值有理函數可以看作是求解線性方程組，所以通過前面介紹的「Secure Linear Algebra」，可以安全（不洩露額外資訊）的計算「degree test」，換句話說，這能判斷交集大小是否小於$n-t$，同時不洩露額外資訊。

3、多方計算交集

這裡的方法可以看作是【The communication complexity of threshold private set intersection 】的推廣。

各方將其資料進行編碼為多項式$P_{S_i}(x)=(x-a_1^{(i)})...(x-a_n^{(i)}),i\in [1, N]$，並且知道交集大小$> n-t$，各方聯合計算出有理函數$(P_{S_1}+...+P_{S_N})/P_{S_1}$，然後插值$O(t)$個點值，$P_1$方恢復出分母，求出交集。

該方案和【The communication complexity of threshold private set intersection】的不同之處就是，將「OLE calls」換成了基於閾值的PKE（具有加法同態性），可以看成多方OLE的替換。

4、安全性
在UC框架下證明了Cardinality Testing的安全，但還存在一個問題，就是「secure linear algebra」協定不能證明是UC安全的，因為輸入是在公鑰加密的密文，在UC設定中，輸入是來自其他地方。

使用Externalized UC框架解決該問題，在該框架下，安全的「linear algebra ideal functionalities」共用公鑰，每人一個私鑰的分享份，使用這種方法證明協定的安全性。

由於「secure linear algebra」協定是安全的，如果它們都共用相同的公鑰，那麼在「Cardinality Testing」中，我們只需要建立此公鑰並共用，所以我們可以證明「Cardinality Testing」是UC安全的。

其他的證明方式：僅證明住主協定的安全性，而不單獨證明每個字協定的安全性。

推薦參考：UC安全，接下來需要看Externalized UC！

基礎

$S$是一個有限集合，$x\leftarrow S$表示從$S$中隨機取樣，$|S|$表示$S$的勢（cardinality）；$N$個參與者;給出兩個不可區分的分佈$D_1,D_2$；安全引數$\lambda$

閾值的PKE

主要介紹了金鑰生成演演算法和判斷是否為0的加密演演算法

UC框架和理想函數

方案使用UC框架【A new paradigm for cryptographic protocols】分析安全性，在該協定中，只考慮半誠實敵手。

其中：

$Z$是環境
$\pi$是協定
$A$是真實世界
$F$是理想函數
$SIM$是模擬器

理想情況下的基於閾值的多方PSI：

只有當交集夠大時，各方才會求交集。

Externalized UC of Global Setup：
externalized UC emulation (EUC)來源於【Universally composable security with global setup】，這是全域性設定（global setup）的UC框架（簡單版）

多項式插值

下面介紹使用一個隨機多項式去「混淆/遮蓋」一個級數小於t的多項式：

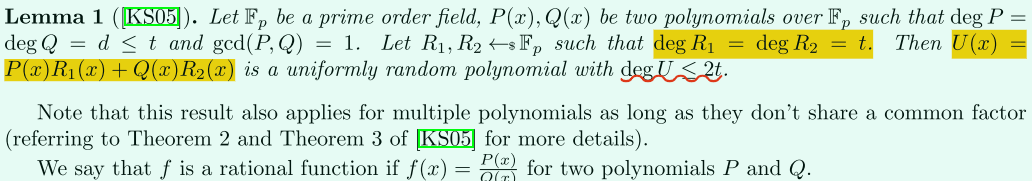
這種方式也可以用於多個多項式（多方），只要他們不共用一個因子（common factor）。

什麼意思，不能約麼？

下面介紹如何通過插值恢復出這個有理函數$f(x)=P(x)/Q(x)$以及證明該函數是唯一的

其中$P(x)$的級數為$m$，$Q(x)$的級數為$n$，則$f(x)$可一通過插值$m+n+1$個點唯一的插值出$f(x)$，若$P(x),Q(x)$是首一的（monic），則只需要$m+n$個點。

給定集合$V=(x,y)$，大小為$m_1+m_2+1$，可以根據這$V$個點唯一的插值出$f(x)=P(x)/Q(x)$。

引理

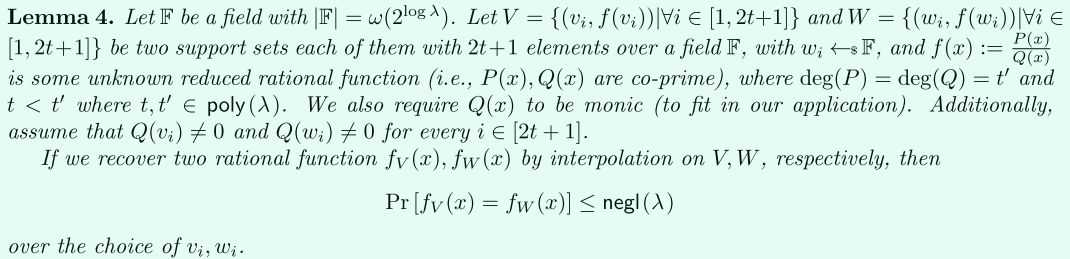
Oblivious Degree Test for Rational Functions

下面給出一個多方協定下求線性計算$Mx=y$，通訊複雜度為$O(t^2k\lambda N)$。

多方求線性函數（Oblivious Linear Algebra）

多方求加密矩陣乘

功能是：

具體實現如下：
（1）初始化：各方$P_i$，共用公鑰$pk$，以及每方各有一份私鑰分享份$sk_i$
（2）輸入：$P_1$輸入兩個矩陣的加密$Enc(pk,M_l),Enc(pk,M_r)$,其中$M_l,M_r\in F^{t*t}$
（3）輸出：各方得到$Enc(M_l*M_r)$

其思想就是：$(a_1+a_2+a_3)(b_1+b_2+b_3)-a_2(b_1+b_2+b_3)-a_3(b_1+b_2+b_3)=a_1b_1 $

但存在一個問題：（以三方為例）

最後得到的$e=Enc(M_l*M_r)+Enc(R_r^{(1)}*R_r^{(1)})+Enc(R_r^{(2)}*R_r^{(2)})+Enc(R_r^{(3)}*R_r^{(3)})$，因為在上面框紅處，沒有自乘！

多方求加密矩陣的秩

功能：

具體實現如下：

其中$F_{OMM}$表示的是以$O(log t)批次處理$計算$t$次乘法

不太懂

多方求線性函數

思想是將問題約減為最小多項式。
$M$是一個非奇異矩陣（non-singular matrix），也叫做滿秩矩陣。
$M,x,y$都是密文形式。
功能：

具體實現如下：

多方勢檢測（Oblivious Degree Test）

功能：判斷多方的交集數量$t'$是否大於閾值$t$，若滿足，則輸出1，否則輸出0。

主要思想是：
在兩個不同資料集上插值出有理函數，並檢查兩次實驗的結果是否相同。
插值有理函數可以看作求解線性函數，因此可以使用「secure linear algebra」求解線性函數。
最後各方只需要安全的檢查$C_v^{(1)}C_w^{(2)}-C_w^{(1)}C_v^{(2)}=0$是否成立！

給定有理函數$P(x)/Q(x)$，其中$P(x),Q(x)$有相同的級數，並給定兩個集合$V_1,V_2$，下面的協定$secDT$是判斷這個有理數函數的級數是否小於閾值$t$：

下面具體來分析一波：
（1）初始化

各方共用公鑰$pk$，且每人有一個私鑰份$sk_i$；
假設各方可以正常執行理想函數：$F_{ORank},F_{OLS},F_{OMM},F_{DecZero}$；
各方共用一組亂數$(\alpha_1,...,\alpha_{4t+2}$；

（2）參與方$P_1$輸入
輸入：$((\alpha_1,Enc(pk,f_1)),...,(\alpha_{4t+2},Enc(pk,f_{4t+2})))$，其中$f_i=P_1(\alpha_i)/P_2(\alpha_i)$，$P_1(x),P_2(x)$是兩個級數為$t'$的多項式

（3）$P_1$設定
將$P_1$的輸入$((\alpha_1,Enc(pk,f_1)),...,(\alpha_{4t+2},Enc(pk,f_{4t+2})))$拆分為兩部分$(\alpha_j,Enc(pk,f_j))_{j\in [2t+1]}=(v_j,Enc(pk,f_{v,j})))_{j\in [2t+1]}$和$(\alpha_j,Enc(pk,f_j))_{j\in (2t+2,...,4t+2)}=(w_j,Enc(pk,f_{w,j})))_{j\in [2t+1]}$。

所以得到了$4t+2$對點值$(v_j,Enc(pk,f_{v,j})_{j\in [2t+1]}$和$(w_j,Enc(pk,f_{w,j})_{j\in [2t+1]}$。

由上面的點值構造兩個密態線性系統：

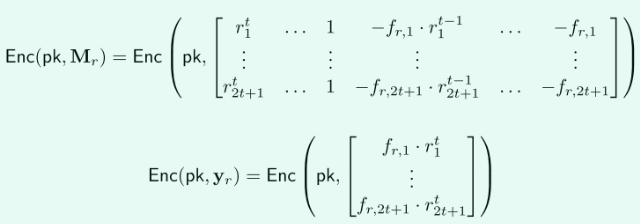
其中$r=(v,w)$，$M_r$是一個維數為$2t+1$的方陣，$y_r$是一個長度為$2t+1$的向量。

這樣就得到了加密的$M_v,y_v$和$M_w,y_w$。
（4）各方聯合計算
計算：$Enc(pk,rank(M_r)-rank([M_r || y]))$，如果結果不為0，則停止協定，其中使用了兩次$F_{ORank}$和$F_{DecZero}$。

即參與方聯合測試$Enc(pk,rank(M_v)-rank([M_v || y_v]))$和$Enc(pk,rank(M_w)-rank([M_w || y_w]))$解密後是否為0，若為0，則繼續。
（5）各方聯合計算
利用$F_{OLS}$計算上面的兩個線性函數，每方得到$Enc(pk,(c_v^{(1)}||c_v^{(2)}))$和$Enc(pk,(c_w^{(1)}||c_w^{(2)}))$，其中$M_r[c_r^{(1)},c_r^{(2)}]=y_r,r\in(v,w)$；$c_r^{(1)}$和$c_r^{(2)}$各是長度為$t+1$和$t$的向量。

這時各方能根據$M_r[c_r^{(1)},c_r^{(2)}]=y_r,r\in(v,w)$由$(y_v,M_v)$得到密態的$c_v^{(1)}||c_v^{(2)}$，$(y_w,M_w)$得到密態的$c_w^{(1)}||c_w^{(2)}$。
（6）各方聯合計算
計算出：$C_v^{(1)}(x)=\sum_{j=0}^{t}c_{v,j}^{(1)}x^{t-j}$，$C_v^{(2)}(x)=x^t+\sum_{j=0}^{t}c_{v,j-1}^{(2)}x^{t-j}$和$C_w^{(1)}(x)=\sum_{j=0}^{t}c_{w,j}^{(1)}x^{t-j}$，$C_w^{(2)}(x)=x^t+\sum_{j=0}^{t}c_{w,j-1}^{(2)}x^{t-j}$

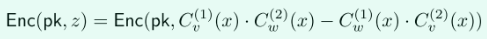
最終計算出密態的$z$。

（7）判斷
各方使用$F_{DecZero}$檢查$z$是否等於0（即對$z$解密）。如果是，輸出0；如果不是，輸出1。

優化

我們考慮在對插值生成$f(x)=P(x)/Q(x)$，當$Q(\alpha_i)=P(\alpha_i)=0$時，我們就不能求$f(x)$了。

解決辦法就是，去掉該點：
使得$\widetilde{P}(x)=P(x)/(x-\alpha _i),\widetilde{Q}(x)=Q(x)/(x-\alpha _i),f(\alpha _i)=\widetilde{P}(\alpha _i)/\widetilde{Q}(\alpha _i)$

具體來講，就是計算出點值對$(\alpha _i,Enc(pk,P_1(\alpha _i)/(x-\alpha _i))$，$(\alpha _i,Enc(pk,P_2(\alpha _i)/(x-\alpha _i)))$。

這裡的$P_1(),P_2(X)$指的是$P(x),Q(x)$

然後再分別構造出$Enc(pk,M_r),Enc(pk,y_r)$，後面的不變。

另外協定也能推廣到$deg(P(x))\neq deg(Q(x))$的情況。

多方閾值PSI

該協定的重點就是cardinality test protocol，能夠安全的判斷N方資料的交集和閾值的大小關係。

安全的勢檢測（Secure Cardinality Testing）

1、理想功能

2、具體實現

總結一下：
（1）各方先各自將資料編碼為多項式，然後求出$4t+2$個點值，加密這些點，得到$4t+2$個密態值$Enc(pk,r_i*P_i(\alpha_j))$，廣播出去。
（2）$P_1$得到$4t+2$個$c_i^{(j)}$，計算得到$d^{(j)}$，形成密態點值對$(\alpha_j,d^{(j)})$，並和私鑰$sk_1$一起傳送給理想函數$F_{SDT}$。
（3）其他參與方$P_2,...,P_N$也將各自的私鑰$sk_i$傳送給理想函數$F_{SDT}$，從而判斷分子$P_1(x)$和分母$P_2(x)$的級數是否最大為$t$，然後輸出結果。

完整的多方閾值PSI協定

在該協定中，通過使用TPKE擴充套件了之前的方案，具體協定如下：

總結一下：
（1）各方先將資料傳送給理想函數$F_{MPCT}$，檢測交集大小和閾值的大小關係。
（2）再通過理想函數$F_{Gen}$生成金鑰：各方共用公鑰$pk$，各自有一個私鑰份$sk_i$。
（3）各方執行：

將資料$S_i$編碼為多項式$P_i(x)$，計算出$3t+_1$個點值$P_i(\alpha_j)$。
取樣$R_i(x)$，使得$deg(R_i(x))=t$。
加密：$c_i^{(j)}=Enc(pk,R_i(\alpha_j)*P_i(\alpha_j))$，然後廣播出去。

（4）$P_1$將收到的對應的密文相加得到$3t+1$個值$d^{(j)}=\sum_{i}^{N}c_i^{(j)}$，再將其廣播出去。
（5）聯合解密出$V^{(j)}=Dec(sk,d^{(j)})$。
（6）$P_1$計算點$\widetilde{V}^{(j)}=V^{(j)}/P_1(\alpha_j)$，得到點值對$(\alpha_j,\widetilde{V}^{(j)})$，將其插值出函數$\widetilde{V}^{(j)}(x)$，再恢復出分母$P_{S_1\setminus (\cap S_i )}(x)$。
（7）$P_1$根據自己資料$S_1=(a_1^{(1)},...,a_1^{(n)})$計算出$P_{S_1\setminus (\cap S_i )}(a_1^{(j)})$，根據$P_{S_1\setminus (\cap S_i )}(a_1^{(j)})\neq 0$，判斷$a_1^{(j)}$是否在交集中。
（8）廣播交集。

在這裡給出了詳細如何根據$P_{S_1\setminus (\cap S_i )}(x)$，計算出交集！

正確性證明：

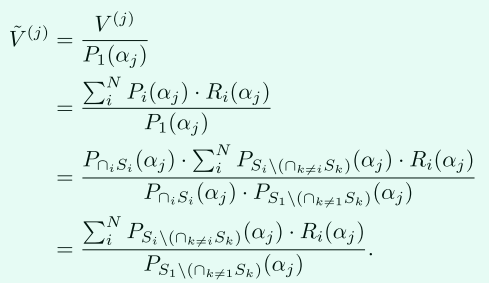
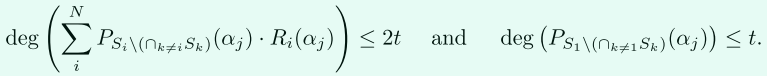
這樣就能根據$3t+1$個點插值出$\widetilde{V}^{(j)}(x)$，再「恢復」出分母$P_{S_1\setminus (\cap S_i )}(x)$，進而帶入資料元素判斷是否為交集元素。

總結

1、關鍵點「cardinality test protocol」，也是最難理解的
2、如何根據$f(x)$恢復出分母？