論文資訊

論文標題：Attributed Graph Clustering via Adaptive Graph Convolution
論文作者：Xiaotong Zhang, Han Liu, Qimai Li, Xiao-Ming Wu
論文來源：2019, IJCAI
論文地址：download 
論文程式碼：download 

1 Introduction

　　關於GNN 是低通濾波器的好文。

2 Method

2.1 Graph Convolution

2.1.1 Basic idea

　　為正式定義圖折積，首先引入圖訊號和圖濾波器的概念。

　　圖訊號可以表示為一個向量 $\boldsymbol{f}= \left[f\left(v_{1}\right), \cdots, f\left(v_{n}\right)\right]^{\top}$，其中 $f: \mathcal{V} \rightarrow \mathbb{R}$ 是一個實值函數。

• • 鄰接矩陣 $A$
  • 度矩陣 $D=\operatorname{diag}\left(d_{1}, \cdots, d_{n}\right)$
  • 對稱標準化圖拉普拉斯矩陣 $L_{s}=I-D^{-\frac{1}{2}} A D^{-\frac{1}{2}}$

　　$L_{s}$ 可特徵分解：$L_{s}=U \Lambda U^{-1}$，其中 $\Lambda= \operatorname{diag}\left(\lambda_{1}, \cdots, \lambda_{n}\right)$ 是按特徵值升序的對角矩陣，$U=\left[\boldsymbol{u}_{1}, \cdots, \boldsymbol{u}_{n}\right]$ 是對應的正交特徵向量。

　　圖濾波器 可表示為 $G= U p(\Lambda) U^{-1} \in \mathbb{R}^{n \times n}$，其中 $p(\Lambda)=\operatorname{diag}\left(p\left(\lambda_{1}\right), \cdots, p\left(\lambda_{n}\right)\right)$ 被稱為 頻率響應函數。

　　圖折積 被定義為 圖訊號 與 圖濾波器 $G$ 的乘法：

　　　　$\overline{\boldsymbol{f}}=G \boldsymbol{f} \quad\quad\quad(1)$

　　其中，$\overline{\boldsymbol{f}}$ 為濾波後的圖訊號。

　　特徵矩陣 $X$ 的 每一列 可看作是一個圖訊號。在圖訊號處理中，特徵值 $\left(\lambda_{q}\right)_{1 \leq q \leq n}$ 可以作為 頻率，相關的特徵向量 $\left(\boldsymbol{u}_{q}\right)_{1 \leq q \leq n}$ 可以作為圖的傅立葉基。一個圖訊號 $f$ 可以被分解為一個特徵向量的線性組合，即，

　　　　$\boldsymbol{f}=U \boldsymbol{z}=\sum\limits_{q=1}^{n} z_{q} \boldsymbol{u}_{q} \quad\quad\quad(2)$

　　式中，$\boldsymbol{z}=\left[z_{1}, \cdots, z_{n}\right]^{\top}$ 和 $z_{q}$ 為 $\boldsymbol{u}_{q}$ 的係數。係數 $\left|z_{q}\right|$ 的大小表示 $\boldsymbol{f}$ 中表示的基訊號 $\boldsymbol{u}_{q}$ 的強度。

　　如果圖上附近的節點具有相似的特徵表示，則圖訊號是平滑的。基訊號 $\boldsymbol{u}_{q}$ 的平滑度可以用 拉普拉斯-貝爾特拉米運算元 $\Omega(\cdot)$ 來測量，即，

　　　　$\begin{aligned}\Omega\left(\boldsymbol{u}_{q}\right) &=\frac{1}{2} \sum\limits_{\left(v_{i}, v_{j}\right) \in \mathcal{E}} a_{i j}\left\|\frac{\boldsymbol{u}_{q}(i)}{\sqrt{d_{i}}}-\frac{\boldsymbol{u}_{q}(j)}{\sqrt{d_{j}}}\right\|_{2}^{2} \\&=\boldsymbol{u}_{q}^{\top} L_{s} \boldsymbol{u}_{q}=\lambda_{q}\end{aligned}\quad\quad\quad(3)$

　　其中，$\boldsymbol{u}_{q}(i)$ 表示向量 $\boldsymbol{u}_{q}$ 的第 $i$ 個元素。

　　$Eq.3$ 表示與較低頻（較小特徵值）相關的基訊號更平滑，即平滑的圖訊號 $f$ 應該比高頻圖訊號包含更多的低頻基訊號。這可通過與低通圖濾波器 $G$ 進行圖折積來實現，如下所示。

　　通過 $Eq.2$，圖折積可以寫成

　　　　$\overline{\boldsymbol{f}}=G \boldsymbol{f}=U p(\Lambda) U^{-1} \cdot U \boldsymbol{z}=\sum\limits_{q=1}^{n} p\left(\lambda_{q}\right) z_{q} \boldsymbol{u}_{q}  \quad\quad\quad(4)$

　　在濾波後的訊號 $\overline{\boldsymbol{f}}$ 中，基訊號 $\boldsymbol{u}_{q}$ 的係數 $z_{q}$ 按 $p\left(\lambda_{q}\right)$ 進行縮放。為保持低頻基訊號和去除 $f$ 中的高頻訊號，圖濾波器 $G$ 應該是低通的，即 頻率響應函數 $p(\cdot)$ 應該是 減小 的和 非負 的。

　　低通圖濾波器可以有多種形式。在這裡，本文設計了一個具有頻率響應函數的低通圖濾波器

　　　　$p\left(\lambda_{q}\right)=1-\frac{1}{2} \lambda_{q}\quad\quad\quad(5)$

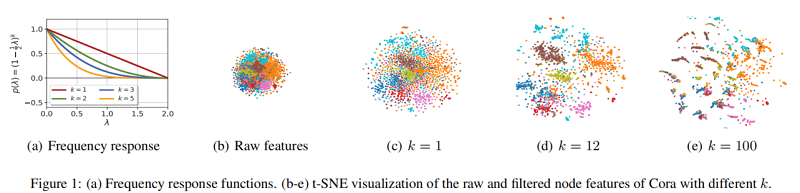
　　如 Figure 1(a) 中的紅線所示，可以看到 $Eq.5$ 中的 $p(\cdot)$ 在 $[0,2]$ 上呈遞減趨勢，且為非負值。

　　

　　注意，對稱歸一化圖拉普拉斯l的所有特徵值 $\lambda_{q}$ 都屬於區間 $[0,2]$，這表明 $Eq.5$ 中的  $p(\cdot)$ 是低通的。在 $Eq.5$ 中以 $p(\cdot)$ 為頻率響應函數的圖濾波器 $G$ 可以寫成

　　　　$G=U p(\Lambda) U^{-1}=U\left(I-\frac{1}{2} \Lambda\right) U^{-1}=I-\frac{1}{2} L_{s}\quad\quad\quad(6)$

　　　　$\bar{X}=G X\quad\quad\quad(7)$

　　其中，$\bar{X}=\left[\overline{\boldsymbol{x}}_{1}, \overline{\boldsymbol{x}}_{2}, \cdots, \overline{\boldsymbol{x}}_{n}\right]^{\top} \in \mathbb{R}^{n \times d}$ 是圖折積後過濾後的節點特徵。在特徵矩陣上應用這樣種低通圖濾波器，使相鄰節點在每個維上具有相似的特徵值，即圖訊號是平滑的。

　　請注意，在 $Eq.6$ 中提出的圖濾波器不同於在 GCN 中使用的圖濾波器。GCN 中的圖濾波器是 $G=   I-L_{s}$，頻率響應函數 $p\left(\lambda_{q}\right)=1-\lambda_{q}$，這顯然不是低通，因為它在 $\lambda_{q} \in(1,2]$ 為負。

 GCN 的濾波器

　　　　$\begin{aligned}\tilde{D}^{-1 / 2} \tilde{A} \tilde{D}^{-1 / 2} &=\tilde{D}^{-1 / 2}(\tilde{D}-L) \tilde{D}^{-1 / 2} \\&=I-\tilde{D}^{-1 / 2} L \tilde{D}^{-1 / 2} \\&=I-\tilde{L}_{s}\end{aligned}$

　　由於 $\tilde{L}_{s}$ 可以被正交對角化，設 $\tilde{L}_{s}=V \tilde{\Lambda} V^{\mathrm{T}}$ ， $\tilde{\lambda}_{i}$ 是 $\tilde{L}_{s}$ 的特徵值，可以證明 $\tilde{\lambda}_{i} \in[0,2)$。
　　因此上式變為:

　　　　$I-V \tilde{\Lambda} V^{T}=V(1-\tilde{\Lambda}) V^{\mathrm{T}}$

　　顯然，其頻率響應函數為  $p(\lambda)=1-\tilde{\lambda}_{i} \in[-1,1)$ 。

2.1.2 k-Order Graph Convolution

　　為了便於聚類，希望同一類的節點在經過圖過濾後應該具有相似的特徵表示。然而，$Eq.7$ 中的一階圖折積可能不足以實現這一點，特別是對於大型稀疏圖，因為它只通過一個節點的聚合來更新每個節點 $v_i$，而不考慮長距離鄰域關係。為了捕獲全域性圖的結構並便於聚類，建議使用 $k$ 階圖的折積。

　　　　$\bar{X}=\left(I-\frac{1}{2} L_{s}\right)^{k} X\quad\quad\quad(8)$

　　其中 $k$ 為正整數，對應的圖濾波器為

　　　　$G=\left(I-\frac{1}{2} L_{s}\right)^{k}=U\left(I-\frac{1}{2} \Lambda\right)^{k} U^{-1}  \quad\quad\quad(9)$

　　在 $Eq.9$ 中，$G$ 的頻率響應函數為

　　　　$p\left(\lambda_{q}\right)=\left(1-\frac{1}{2} \lambda_{q}\right)^{k} \quad\quad\quad(10)$

　　如 Figure 1(a) 所示，隨著 $k$ 的增加，$Eq.10$ 中的 $p\left(\lambda_{q}\right)$ 變得更低通，說明濾波後的節點特徵 $\bar{X}$ 將更平滑。

　　$k$ 階圖折積的迭代計算公式為

　　　　$\begin{array}{l} \overline{\boldsymbol{x}}_{i}^{(0)}=\boldsymbol{x}_{i}\\ \overline{\boldsymbol{x}}_{i}^{(1)}=\frac{1}{2}\left(\overline{\boldsymbol{x}}_{i}^{(0)}+\sum\limits_{\left(v_{i}, v_{j}\right) \in \mathcal{E}} \frac{a_{i j}}{\sqrt{d_{i} d_{j}}} \overline{\boldsymbol{x}}_{j}^{(0)}\right)\\\vdots \\\overline{\boldsymbol{x}}_{i}^{(k)}=\frac{1}{2}\left(\overline{\boldsymbol{x}}_{i}^{(k-1)}+\sum\limits_{\left(v_{i}, v_{j}\right) \in \mathcal{E}} \frac{a_{i j}}{\sqrt{d_{i} d_{j}}} \overline{\boldsymbol{x}}_{j}^{(k-1)}\right)\end{array} \quad\quad\quad(11)$

　　最終的 $\overline{\boldsymbol{x}}_{i}$ 是 $\overline{\boldsymbol{x}}_{i}^{(k)}$。

Note

　　因為：

　　　　${\large \bar{X}=\left(I-\frac{1}{2} L_{s}\right) X=\frac{1}{2}\left(I+D^{-\frac{1}{2}} A D^{-\frac{1}{2}}\right) X} $

　　所以：

　　　　${\large \overline{x_{i}}=\frac{1}{2}\left(x_{i}+\sum\limits_{\left(v_{i}, v_{j}\right) \in e} \frac{a_{i j}}{\sqrt{d_{i} d_{j}}} x_{j}\right)} $

　　隨著 $k$ 增加，$k$ 階圖折積將使節點特徵在每個維度上更平滑。下面，我們使用 $Eq.3$ 中定義的拉普拉斯-貝爾特拉米運算元 $\Omega(\cdot)$ 來證明這一點。用 $f$ 表示特徵矩陣 $X$ 的一列，可以分解為 $\boldsymbol{f}=U \boldsymbol{z}$。請注意， $\Omega(\beta \boldsymbol{f})=\beta^{2} \Omega(\boldsymbol{f})$，其中 $\beta$ 是一個標量。因此，為了比較不同的圖訊號的平滑性，我們需要把它們放在一個共同的尺度上。接下來，我們考慮一個歸一化訊號 $\frac{f}{\|f\|_{2}}$ 的平滑性，即，

　　　　$\Omega\left(\frac{\boldsymbol{f}}{\|\boldsymbol{f}\|_{2}}\right)=\frac{\boldsymbol{f}^{\top} L_{s} \boldsymbol{f}}{\|\boldsymbol{f}\|_{2}^{2}}=\frac{\boldsymbol{z}^{\top} \Lambda \boldsymbol{z}}{\|\boldsymbol{z}\|_{2}^{2}}=\frac{\sum\limits_{i=1}^{n} \lambda_{i} z_{i}^{2}}{\sum\limits_{i=1}^{n} z_{i}^{2}} \quad\quad\quad(12)$

證明：

　　

　　我們現在可以用這個引理來證明 Theorem 1。為方便起見，我們將 $L_{s}$ 的特徵值 $\lambda_{i}$ 按遞增順序排列為 $0 \leq \lambda_{1} \leq \cdots \leq \lambda_{n}$。由於 $p(\lambda)$ 是非增加的和非負的，所以 $p\left(\lambda_{1}\right) \geq \cdots \geq p\left(\lambda_{n}\right) \geq 0$。可以用上述引理來證明Theorem 1 ，通過設定 ：

　　　　$T_{i}=\lambda_{i}, \quad b_{i}=z_{i}^{2}, \quad c_{i}=p^{2}\left(\lambda_{i}\right) z_{i}^{2} \quad\quad\quad(16)$

　　假設 $\boldsymbol{f}$ 和 $\overline{\boldsymbol{f}}$ 分別由 $(k−1)$ 階和 $k$ 階圖折積得到，我們可以立即從 Theorem 1 中推斷出 $\overline{\boldsymbol{f}}$ 比 $\boldsymbol{f}$ 更平滑。換句話說，$k$ 階圖折積會隨著 $k$ 的增加而產生更平滑的特徵。由於同一叢集中的節點傾向於緊密連線，它們可能具有更多具有大 $k$ 的相似特徵表示，這有利於聚類。

2.2 Clustering via Adaptive Graph Convolution

　　演演算法如下：

　　

　　為了自適應地選擇 $k$ 階，我們使用聚類效能度量-僅基於資料的內在資訊的內部標準。在這裡，我們考慮 intra-cluster distance(對於給定的簇 $\mathcal{C}$)，它表示 $\mathcal{C}$ 的緊緻性：

　　　　$\operatorname{intra}(\mathcal{C})=\frac{1}{|\mathcal{C}|} \sum\limits_{C \in \mathcal{C}} \frac{1}{|C|(|C|-1)} \sum\limits_{\substack{v_{i}, v_{j} \in C, v_{i} \neq v_{j}}}\left\|\bar{x}_{i}-\bar{x}_{j}\right\|_{2}$

　　需要注意的是，在具有固定資料特徵的情況下，簇間距離也可以用來度量聚類效能，良好的簇類劃分應該具有較大的簇間距離和較小的簇內距離。然而，根據 Theorem 1，隨著 $k$ 的增加，節點特徵變得更平滑，這可以顯著減少簇內和簇間的距離。因此，簇間的距離可能不是衡量叢集效能的可靠度量指標因此，我們建議觀察選擇 $k$ 的簇內距離的變化。

　　所以，最後的選擇簇分配為 $\mathcal{C}^{(t-1)}$。這種選擇策略的好處是有兩方面的。首先，它確保為 $\text{intra }  (\mathcal{C})$ 找到一個區域性最小值，這可能表明一個良好的簇分配，並避免過度平滑。其次，停止在 $\text{intra }  (\mathcal{C})$  內的第一個區域性最小值是時間有效的。

3 Experiments

　　

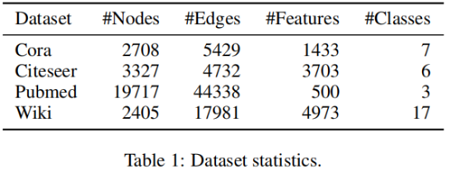
節點聚類

　　

4 Conclusion

　　本文提出了一種簡單而有效的屬性圖聚類方法。為了更好地利用可用資料和捕獲全域性叢集結構，我們設計了一個k階圖折積來聚合遠端資料資訊。為了優化不同圖上的聚類效能，我們設計了一種自適應選擇合適的k的策略。這使得我們的方法能夠達到與經典的和最先進的方法相比的競爭效能。在未來的工作中，我們計劃改進自適應選擇策略，使我們的方法更加魯棒和高效。

修改歷史

2022-06-30 建立文章

 

論文解讀目錄