一、4數種類分析

統計分析

從標有1-10的數位的10個小球中取出1個小球記錄小球的數位，然後將小球放回，如此反覆4次取出4小球的數位組成的序號一共有多少種。注意：1.1.8.9 和1.8.1.9 算是一種。

需要分為一下幾種情況：

四個小球數位都相等情況：

一個有10種

三個小球數位相等：

一共有10*9種 = 90

兩個小球數位相等，另外兩個小球數位不相等

一共有10 * ( 9 * 8 /2 )種 = 360

10表示：10個相等的兩個小球

( 9 * 8 /2 )表示：另外兩個小球不相等的情況。

兩個小球數位相等，另外兩個小球也相等。

一共有(10*9)/2 中 = 45

四個小球數位都不想等

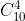
$C_{10}^{4}$ 編輯 = 10* 9 * 8 * 7 / (4 * 3 *2 *1 ) = 210

總數為=10 + 90 + 360 + 45 + 210 = 715

程式碼分析

程式碼中我們可以直接使用遍歷的方式進行窮舉，

1 . 對比記錄列表中的資料是否存在，如果存在就忽略。

2. 如果不存在就新增到列表中。

遍歷所有的資料。

#define MAXNUM 10
QList<struNum> initList()
{
    QList<struNum> list;
    for (int i1 = 1;i1 <= MAXNUM; i1++) {
        for (int i2 = 1;i2 <= MAXNUM; i2++) {
            for (int i3 = 1;i3 <= MAXNUM; i3++) {
                for (int i4 = 1;i4 <= MAXNUM; i4++) {
                    struNum num(i1,i2,i3,i4);
                    if(!isInList(num,list)){
                        list.append(num);
                    }
                }
            }
        }
    }
    return list;
}

判斷是否存在列表中

typedef  struct SNUM{
    SNUM(int num1,int num2,int num3,int num4){
        this->num1 = num1;
        this->num2 = num2;
        this->num3 = num3;
        this->num4 = num4;
    }
    int num1 =0;
    int num2 =0;
    int num3 =0;
    int num4 =0;
    int c = 0;  // 四個數能夠計算24演演算法。
}struNum;
bool isInList(struNum num, QList<struNum> list)
{
    int numList[4] = {num.num1,num.num2,num.num3,num.num4};
    bool result = false;
    for (int i1 = 0 ; i1 < 4; i1 ++) {
        for (int i2 = 0 ; i2 < 4; i2 ++){
            if(i1 == i2) continue;
            for (int i3 = 0 ; i3 < 4; i3 ++){
                if(i2 == i3 || i1 == i3) continue;
                for (int i4 = 0 ; i4 < 4; i4 ++){
                    if(i1 == i4 || i2 == i4 || i3 == i4) continue;
                      foreach(auto item ,list){
                            if(item.num1 == numList[i1]
                                && item.num2 == numList[i2]
                                && item.num3 == numList[i3]
                                && item.num4 == numList[i4]){
                                result = true;
                            }
                      }
                }
            }
        }
    }
    return result;
}

二、四數排列演演算法分析

4個數按照順序排列，一共有多少種排列方法。

我們可以使用遍歷方法，將所有的數位進行遍歷，那麼可以得到一下演演算法。可以看到以下演演算法的步驟需要經過4*4*4*4 次運算。那麼我們通過觀察可以優化程式碼演演算法。

優化前

4*4*4*4 = 256次運算

   int numList[4] = {num1,num2,num3,num4};

   for (int i1 = 0 ; i1 < 4; i1 ++) {
        for (int i2 = 0 ; i2 < 4; i2 ++){
            for (int i3 = 0 ; i3 < 4; i3 ++){
                for (int i4 = 0 ; i4 < 4; i4 ++){
                  if(i1 != i2 && i1 != i3 && i1 != i4 && i2 != i3 && i2 != i4 && i3 != i4){
                        qInfo()<<numList[i1]<<" "<<numList[i2] <<" "<< numList[i3] <<" "<<" "<< numList[i4];
                        c++;
                   }
                }
            }
        }
    }
點選並拖拽以移動

優化後

4*3*2 = 24 次運算。

 1 int numList[4] = {num1,num2,num3,num4};
 2     int c =0;
 3     for (int i1 = 0 ; i1 < 4; i1 ++) {
 4         for (int i2 = 0 ; i2 < 4; i2 ++){
 5             if(i1 == i2) continue;
 6             for (int i3 = 0 ; i3 < 4; i3 ++){
 7                 if(i2 == i3 || i1 == i3) continue;
 8                 for (int i4 = 0 ; i4 < 4; i4 ++){
 9                     if(i1 == i4 || i2 == i4 || i3 == i4) continue;
10                      qInfo()<<numList[i1]<<" "<<numList[i2] <<" "<< numList[i3] <<" "<<" "<< numList[i4];
11                         c++;
12                 }
13             }
14         }
15     }

三、分數計算類

由於計算過程中可能會遇到分數計算，因此我們不能使用int型別直接表示資料，或者是資料運算結果，我們定義一個分數類，專門用來計算分數的，加、減、乘、除，這樣可以儘可能儲存資料的正確性。

加法

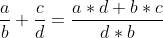
$\frac{a}{b}+\frac{c}{d}=\frac{a*d+b*c}{d*b}$ 編輯

減法

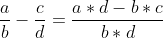
$\frac{a}{b}-\frac{c}{d} = \frac{a*d-b*c}{b*d}$ 編輯

乘法

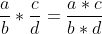
$\frac{a}{b}*\frac{c}{d} = \frac{a*c}{b*d}$ 編輯

除法

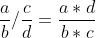
$\frac{a}{b}/\frac{c}{d}=\frac{a*d}{b*c}$ 編輯

LNum.h

 1 #ifndef LNUM_H
 2 #define LNUM_H
 3 
 4 class LNum
 5 {
 6 
 7 public:
 8     LNum(int Molecule);
 9     LNum(int Molecule,int Denominator);
10     int getMolecule();                   // 獲取分子
11     int getDenominator();                // 獲取分母
12     void setMolecule(int molecule);      // 設定分子
13     void setDenominator(int denominator);// 設定分母
14     double data();
15     LNum operator + ( LNum p1);
16     LNum operator - ( LNum p1);
17     LNum operator * ( LNum p1);
18     LNum operator / ( LNum p1);
19     bool operator ==( LNum p1) ;
20 private:
21     // 分子
22     int m_iMolecule = 1;
23     // 分母
24     int m_iDenominator = 1;
25     void Equivalency();         // 約分
26 
27 };
28 
29 #endif // LNUM_H

LNum.cpp

  1 #include "lnum.h"
  2 
  3 
  4 LNum::LNum(int num)
  5     :m_iMolecule(num)
  6     ,m_iDenominator(1)
  7 {
  8 
  9 }
 10 
 11 LNum::LNum(int Molecule, int Denominator)
 12     :m_iMolecule(Molecule)
 13     ,m_iDenominator(Denominator)
 14 {
 15 
 16 }
 17 
 18 int LNum::getMolecule()
 19 {
 20     Equivalency();
 21     return m_iMolecule;
 22 }
 23 
 24 int LNum::getDenominator()
 25 {
 26     Equivalency();
 27     return  m_iDenominator;
 28 }
 29 
 30 void LNum::setMolecule(int molecule)
 31 {
 32     m_iMolecule = molecule;
 33 }
 34 
 35 void LNum::setDenominator(int denominator)
 36 {
 37     m_iDenominator = denominator;
 38 }
 39 
 40 double LNum::data()
 41 {
 42     Equivalency();
 43     if(m_iDenominator == 1){
 44         return m_iMolecule;
 45     }
 46     return double(m_iMolecule)/double(m_iDenominator);
 47 }
 48 
 49 void LNum::Equivalency()
 50 {
 51     int num = m_iMolecule> m_iDenominator?m_iDenominator:m_iMolecule;
 52 
 53     for (int i  = 2 ; i < num ;i++) {
 54         if(m_iDenominator%i == 0 && m_iMolecule%i ==0){
 55             m_iDenominator = m_iDenominator/i;
 56             m_iMolecule = m_iMolecule/i;
 57             num = m_iMolecule> m_iDenominator?m_iDenominator:m_iMolecule;
 58         }
 59     }
 60 }
 61 
 62 LNum LNum::operator +(LNum p1)
 63 {
 64     LNum res(getMolecule(),getDenominator());
 65     res.setMolecule(getMolecule()*p1.getDenominator() + getDenominator()*p1.getMolecule());
 66     res.setDenominator(getDenominator()*p1.getDenominator());
 67     return  res;
 68 }
 69 
 70 LNum LNum::operator -(LNum p1)
 71 {
 72     LNum res(getMolecule(),getDenominator());
 73     res.setMolecule(getMolecule()*p1.getDenominator() - getDenominator()*p1.getMolecule());
 74     res.setDenominator(getDenominator()*p1.getDenominator());
 75     return  res;
 76 }
 77 
 78 LNum LNum::operator *(LNum p1)
 79 {
 80     LNum res(getMolecule(),getDenominator());
 81     res.setMolecule(getMolecule()*p1.getMolecule());
 82     res.setDenominator(getDenominator()*p1.getDenominator());
 83     return  res;
 84 }
 85 
 86 LNum LNum::operator /(LNum p1)
 87 {
 88     LNum res(getMolecule(),getDenominator());
 89     res.setMolecule(getMolecule()*p1.getDenominator());
 90     res.setDenominator(getDenominator()*p1.getMolecule());
 91     return  res;
 92 }
 93 
 94 bool LNum::operator ==(LNum p1)
 95 {
 96     if (getMolecule() == p1.getMolecule() && getDenominator() == p1.getDenominator()) {
 97         return true;
 98     }
 99     else{
100         return false;
101     }
102 
103 }

四、加減乘除操作符遍歷

第一步將操作符數位化，方便遍歷。可以得到如下公式。x為操作符標識。

 1 double jisuan(LNum num1,LNum num2,int x){
 2     switch (x) {
 3     case 0:
 4         return num1+num2;
 5     case 1:
 6         return num1-num2 ;
 7     case 2:
 8         return num1*num2;
 9     case 3:
10         return num1/num2 ;
11     }
12     return 0;
13 }

五、探測4個數是否能計算24

迴圈遍歷4個數的不同位置，並且迴圈遍歷演演算法。判斷其內容是否為24如果是24那麼表示可以計算成功。

 1 int is24OK(LNum num1, LNum num2, LNum num3, LNum num4)
 2 {
 3     int result = 0;
 4      QList<struRecordNum> list;
 5     LNum numList[4] = {num1,num2,num3,num4};
 6         // 交換4個數位的順序。
 7         for (int i1 = 0 ; i1 < 4; i1 ++) {
 8             for (int i2 = 0 ; i2 < 4; i2 ++){
 9                 if(i1 == i2) continue;
10                 for (int i3 = 0 ; i3 < 4; i3 ++){
11                     if(i2 == i3 || i1 == i3) continue;
12                     for (int i4 = 0 ; i4 < 4; i4 ++){
13                         if(i1 == i4 || i2 == i4 || i3 == i4) continue;
14                         //  qInfo()<<numList[i1]<<" "<<numList[i2] <<" "<< numList[i3] <<" "<<" "<< numList[i4];
15                           int x=suanfatongji(numList[i1],numList[i2],numList[i3],numList[i4],&list);
16                           if(x !=0){
17                               qInfo()<<"x:"<<x;
18                               result += x;
19                           }
20                     }
21                 }
22             }
23         }
24         return result;
25 }
26 
27 int suanfatongji(LNum num1, LNum num2, LNum num3, LNum num4, QList<struRecordNum> *list)
28 {
29         LNum sum = 0;
30 
31         int c= 0;
32         for(int i1 = 0 ; i1 < 4; i1 ++){
33             for(int i2 = 0 ; i2 < 4; i2 ++ ){
34                 for(int i3 = 0 ; i3 < 4; i3 ++){
35                     sum = jisuan(jisuan(jisuan (num1,num2,i1),num3,i2),num4,i3) ;
36                     if(24.0  == sum.data()){
37                         // 是否找到相同的演演算法，因為有重複數位可能導致演演算法想法和數位相同的情況。
38                         bool result = false;
39                         for(auto item : *list){
40                             if(item.num1 == static_cast<int>(num1.data())
41                             && item.num2 == static_cast<int>(num2.data())
42                             && item.num3 == static_cast<int>(num3.data())
43                             && item.num4 == static_cast<int>(num4.data())
44                             && item.option1 == i1
45                             && item.option2 == i2
46                             && item.option3 == i3){
47                                 result = true;
48                             }
49                         }
50                         if(!result){
51                             struRecordNum tmpItem;
52                             tmpItem.num1 =  static_cast<int>(num1.data());
53                             tmpItem.num2 =  static_cast<int>(num2.data());
54                             tmpItem.num3 =  static_cast<int>(num3.data());
55                             tmpItem.num4 =  static_cast<int>(num4.data());
56                             tmpItem.option1 =  i1;
57                             tmpItem.option2 =  i2;
58                             tmpItem.option3 =  i3;
59                             list->append(tmpItem);
60                              c++;
61                              qInfo()<< "(( "<< num1.data() <<strOption(i1) << num2.data() <<")"<<strOption(i2)<< num3.data()<<")" <<strOption(i3)<< num4.data();
62                         }
63                     }
64                 }
65             }
66         }
67         return c;
68 }

六、原始碼地址

啊淵 / QT部落格案例 · GitCode 24點題庫分析。

24點遊戲題庫演演算法分析

二、四數排列演演算法分析

三、分數計算類

四、加減乘除操作符遍歷

五、探測4個數是否能計算24

六、原始碼地址