論文資訊

論文標題：Efficient Graph Convolution for Joint Node RepresentationLearning and Clustering
論文作者：Chakib Fettal, Lazhar Labiod,Mohamed Nadif
論文來源：2021, WSDM
論文地址：download
論文程式碼：download

1 Introduction

 　　一個統一的框架中解決了節點嵌入和聚類問題。

2 Method

　　　　$Z=\operatorname{enc}\left(\operatorname{agg}(\mathbf{A}, \mathbf{X}) ; \mathbf{W}_{1}\right)=\operatorname{agg}(\mathbf{A}, \mathbf{X}) \mathbf{W}_{1}$

　　Decoder 即一個簡單的線性變換：

　　　　$\operatorname{dec}\left(\mathbf{Z} ; \mathbf{W}_{2}\right)=\mathbf{Z} \mathbf{W}_{2}$

2.3 Normalized Simple Graph Convolution

　　本文的聚合函數受到 SGC [42] 中提出的簡單圖折積的啟發。設為：

　　　　$\operatorname{agg}(\mathbf{A}, \mathbf{X})=\mathbf{T}^{p} \mathbf{X}$

　　其中，$T$ 不是新增了自環的對稱標準化鄰接矩陣，本文 $T$  定義為 ：

　　　　$\mathrm{T}=\mathrm{D}_{\mathrm{T}}^{-1}(\mathrm{I}+\tilde{\mathrm{S}})$

　　其中：

• • $\tilde{\mathrm{S}}=\tilde{\mathbf{D}}^{-1 / 2} \tilde{\mathrm{A}} \tilde{\mathrm{D}}^{-1 / 2}$；
  • $\tilde{\mathrm{A}}=\mathrm{A}+\mathrm{I}$；
  • $\tilde{\mathbf{D}}$ 是從 $\tilde{\mathrm{A}}$ 得出的度矩陣；
  • $\mathrm{D}_{\mathrm{T}}$ 是從 $I + \tilde{\mathrm{S}}$ 得出的度矩陣；

　　GCN 的頻率響應函數 $p(\lambda)=1-\tilde{\lambda}_{i} \in[-1,1)$。

　　SGC 的傳播矩陣為 $\mathbf{I}-\tilde{\mathbf{S}}=\mathbf{I}-\tilde{\mathbf{D}}^{-1 / 2}(\mathbf{I}-\tilde{\mathbf{L}}) \tilde{\mathbf{D}}^{-1 / 2}$，其頻率響應函數為 $h\left(\tilde{\lambda}_{l}\right)=1-\tilde{\lambda}_{l} $，該濾波器在 $[0,1]$ 上是低通的，而不是 $[0,1.5]$。然後，本文建議進一步新增自迴圈和行規範化矩陣 $\tilde{\mathrm{S}}$。這將產生以下影響

• • 從譜域的角度來看：所提出的歸一化進一步縮小了矩陣的譜域到 $[0,1]$ 中，如圖2所示，這使得濾波器真正的低通；
  • 從空間域的角度來看：每個轉換後的頂點成為鄰居的加權平均值，這更直觀，但它也考慮了列度資訊，不像直接隨機遊走鄰接歸一化；

　　本文的問題變成：

　　　　$\begin{array}{l}&\underset{\mathrm{G}, \mathbf{F}, \mathbf{W}_{1}, \mathbf{W}_{2}}{\text{min }}  &\left\|\mathbf{T}^{p} \mathbf{X}-\mathbf{T}^{p} \mathbf{X} \mathbf{W}_{1} \mathbf{W}_{2}\right\|^{2}+\alpha\left\|\mathbf{T}^{p} \mathbf{X} \mathbf{W}_{1}-\mathrm{GF}\right\|^{2} \\&\text { s.t. } &\mathrm{G} \in\{0,1\}^{n \times k}, \mathbf{G 1}_{k}=\mathbf{1}_{n}\end{array}$

2.5 Graph Convolutional Clustering

　　為使得嵌入空間資訊和聚類資訊相互補充，本文設定 $\mathrm{W}=\mathrm{W}_{1}=\mathrm{W}_{2}^{\top}$，並新增一個正交性約束，所以 $Eq.4$ 變為：

　　　　$\begin{array}{l}\underset{\mathrm{G}, \mathrm{F}, \mathbf{W}}{\text{min }}&\left\|\mathrm{T}^{p} \mathbf{X}-\mathbf{T}^{p} \mathbf{X W W}{ }^{\top}\right\|^{2}+\left\|\mathrm{T}^{p} \mathbf{X W}-\mathrm{GF}\right\|^{2} \\\text { s.t. } & \mathrm{G} \in\{0,1\}^{n \times k}, \mathbf{G} \mathbf{1}_{k}=\mathbf{1}_{n}, \mathbf{W}^{\top} \mathbf{W}=\mathbf{I}_{k}\end{array}\quad\quad\quad(5)$

　　與 [43] 類似，該問題等價於

　　　　$\begin{array}{l}\underset{\mathrm{G}, \mathrm{F}, \mathbf{W}}{\text{min }}&\left\|\mathrm{T}^{p} \mathbf{X}-\mathrm{GFW}^{\top}\right\|^{2} \\\text { s.t. } & \mathrm{G} \in\{0,1\}^{n \times k}, \mathbf{G} \mathbf{1}_{k}=\mathbf{1}_{n}, \mathbf{W}^{\top} \mathbf{W}=\mathbf{I}_{k}\end{array}\quad\quad\quad(6)$

證明：

　　首先分解重構項：

　　　　$\begin{aligned}\left\|\mathbf{T}^{p} \mathbf{X}-\mathbf{T}^{p} \mathbf{X W} \mathbf{W}^{\top}\right\|^{2} &=\left\|\mathbf{T}^{p} \mathbf{X}\right\|^{2}+\left\|\mathbf{T}^{p} \mathbf{X W} \mathbf{W}^{\top}\right\|^{2}-2\left\|\mathbf{T}^{p} \mathbf{X W}\right\|^{2} \\&=\left\|\mathbf{T}^{p} \mathbf{X}\right\|^{2}-\left\|\mathbf{T}^{p} \mathbf{X W}\right\|^{2} \quad \text { due to } \mathbf{W}^{\top} \mathbf{W}=\mathbf{I}_{k}\end{aligned}$

　　其次，聚類正則化項分解為：

　　　　$\left\|\mathrm{T}^{p} \mathrm{XW}-\mathrm{GF}\right\|^{2}=\left\|\mathrm{T}^{p} \mathrm{XW}\right\|^{2}+\|\mathrm{GF}\|^{2}-2 \operatorname{Tr}\left(\left(\mathrm{T}^{p} \mathrm{XW}\right)^{\top} \mathrm{GF}\right)$

　　上述兩個結果表示式求和：

　　　　$\begin{array}{r}\left\|\mathbf{T}^{p} \mathbf{X}\right\|^{2}+\|\mathrm{GF}\|^{2}-2 \operatorname{Tr}\left(\left(\mathrm{T}^{p} \mathrm{XW}\right)^{\top} \mathrm{GF}\right)=\left\|\mathrm{T}^{p} \mathrm{X}-\mathrm{GFW}^{\top}\right\|^{2} \\\text { due to }\left\|\mathrm{GFW}{ }^{\top}\right\|=\|\mathrm{GF}\|\end{array}$

　　因此，優化 $\text{Eq.5}$ 等價於優化 $\text{Eq.6}$。

3 Optimization and algorithm

　　該演演算法交替固定 $F$、$G$ 和 $W$ 中兩個矩陣 ，並求解第三個矩陣。

3.1 Optimization Procedure

Initialization

　　對 $\mathbf{T}^{p} \mathbf{X}$ 應用主成分分析(PCA) 得到的前 $f$ 個分量來初始化 $\mathbf{W}$。然後在 $\mathbf{T}^{p} \mathbf{X}$ 上應用 k-means 得到 $\mathbf{F}$ 和 $\mathrm{G}$。

　　通過固定 $\mathrm{G}$ 和 $\mathrm{W}$ 並求解 $\mathbf{F}$，我們得到了一個線性最小二乘問題。通過將導數設為零，得到了對給定問題的最優解的正態方程。然後是更新規則

　　　　$\mathbf{F}=\left(\mathrm{G}^{\top} \mathrm{G}\right)^{-1} \mathrm{G}^{\top} \mathrm{T}^{p} \mathbf{X W}\quad\quad\quad(7)$

　　直觀地說，每個行向量 $\mathrm{f}_{i}$ 被設定為分配給叢集 $i$ 的嵌入 $\mathrm{XW}$ 的平均值。並通過 K-means 更新質心矩陣。

　　固定 $Eq.6$ 中的 $\mathrm{F}$ 和 $\mathrm{G}$，所以更新規則如下：

　　　　$\mathbf{W}=\mathbf{U V}^{\top} \quad \text { s.t. } \quad[\mathrm{U}, \Sigma, \mathrm{V}]=\operatorname{SVD}\left(\left(\mathrm{T}^{p} \mathbf{X}\right)^{\top} \mathrm{GF}\right)$

　　其中，

• • $\Sigma=\left(\sigma_{i i}\right)$　　
  • $U$ 和 $V$ 分別代表 $\left(\mathrm{T}^{p} \mathbf{X}\right)^{\top} \mathrm{GF}$ 的特徵值和左、右特徵向量；

　　固定 $F$ 和 $G$ 產生如下問題：

　　　　$\underset{\mathrm{W}}{\text{min }}\left\|\mathrm{T}^{p} \mathrm{X}-\mathrm{GFW}^{\top}\right\|^{2} \quad \text { s.t. } \quad \mathbf{W}^{\top} \mathbf{W}=\mathbf{I}_{k} .$

　　因為：$\left\|\mathbf{T}^{p} \mathbf{X}-\mathbf{G F W}^{\top}\right\|^{2}=\left\|\mathbf{T}^{p} \mathbf{X}\right\|^{2}+\left\|\mathbf{G F W}^{\top}\right\|^{2}-2 \operatorname{Tr}\left(\mathbf{W F}^{\top} \mathbf{G}^{\top} \mathbf{T}^{p} \mathbf{X}\right)$ 和 $\left\|\mathrm{GFW}^{\top}\right\|^{2}=\|\mathrm{GF}\|^{2}$，所以 $\text{Eq.9}$ 等價於

　　　　$\underset{\mathbf{W}}{\text{max}}\operatorname{Tr}\left(\mathbf{W F}^{\top} \mathbf{G}^{\top} \mathbf{T}^{p} \mathbf{X}\right) \quad \text { s.t. } \quad \mathbf{W}^{\top} \mathbf{W}=\mathbf{I}_{k} .$

　　由於 $[\mathrm{U}, \Sigma, \mathrm{V}]=\operatorname{SVD}\left(\mathbf{F}^{\top} \mathbf{G}^{\top} \mathrm{T}^{p} \mathrm{X}\right)$，所以有

　　　　$\begin{aligned}\operatorname{Tr}\left(\mathbf{W F}^{\top} \mathbf{G}^{\top} \mathbf{T}^{p} \mathbf{X}\right) &=\operatorname{Tr}\left(\mathbf{W} \mathbf{U} \Sigma \mathbf{V}^{\top}\right) \\&=\sum\limits_{i=1}^{f} \sigma_{i i}<\mathbf{w}_{i}^{\prime} \mathbf{U}, \mathbf{v}_{i}^{\prime}>\\& \leq \sum\limits_{i=1}^{f} \sigma_{i i}\left\|\mathbf{w}_{i}^{\prime} \mathbf{U}\right\| \times\left\|\mathbf{v}_{i}^{\prime}\right\|=\sum\limits_{i=1}^{f} \sigma_{i i}=\operatorname{Tr}(\Sigma)\end{aligned}$

　　這意味著當 $\operatorname{Tr}\left(\mathbf{W U \Sigma V ^ { \top }}\right)=\operatorname{Tr}(\Sigma)$ 或當 $\mathbf{V}^{\top} \mathbf{W U}=  I$ 時達到了 $Eq.9$ 的上界，即在 $\mathbf{W}=\mathbf{V U}^{\top} $ 時達到了最大值。

　　通過固定 $F$ 和 $W$ 並求解 $F$，我們得到了一個可以通過 k-means 演演算法的分配步驟進行優化的問題。那麼，更新規則定為

　　　　$g_{i j^{*}} \leftarrow\left\{\begin{array}{ll}1 & \text { if } j^{*}=\arg \min _{j}\left\|\left(\mathbf{T}^{p} \mathbf{X W}\right)_{i}-\mathbf{f}_{j}\right\|^{2} \\0 & \text { otherwise. }\end{array}\right.\quad\quad\quad(10)$

3.2 The GCC Algorithm

　　演演算法步驟如 Algorithm 1 所示：

　　

　　傳播階 $p$ 的選擇對演演算法的整體效能非常重要。較小的 $p$ 可能意味著傳播的鄰域資訊不足，而較大的 $p$  可能導致圖訊號的過度平滑。Figure 3 顯示了使用 t-SNE 演演算法[39]對不同 $p$ 值的 Cora 資料集的投影。

　　

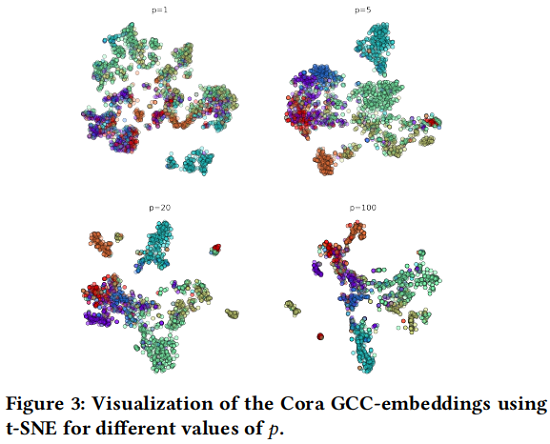
　　對於 $p$ 的選擇如 Algorithm 2 所示：

　　

4 Experiments

資料集

　　

聚類結果

　　

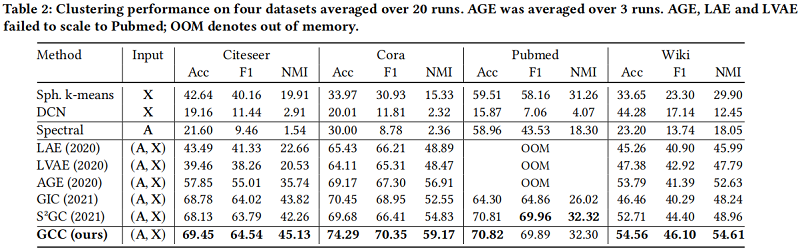
執行時間

　　

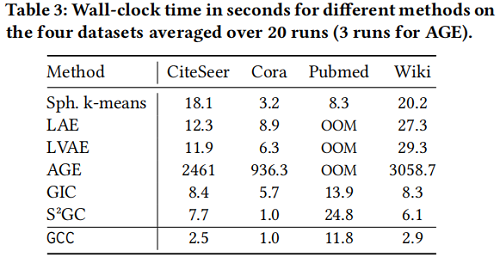
5 Conclusion

　　在本文中，我們利用圖折積網路的簡單公式，得到了一個有效的模型，在一個統一的框架中解決了節點嵌入和聚類問題。首先，我們提供了一個歸一化，使GCN編碼器在嚴格意義上充當低通濾波器。其次，我們提出了一種新的方法，其中需要優化的目標函數利用了來自GCN嵌入重建損失和這些嵌入的簇結構的資訊。第三，我們推導了複雜性被嚴格研究的GCC。在此過程中，我們展示了GCC如何以更有效的方式比其他圖聚類演演算法獲得更好的效能。請注意，所有比較的方法在本質上都是無監督的，以便與我們的模型進行公平的比較。我們的實驗證明了我們的方法的興趣。我們還展示了GCC是如何與其他方法相關的，包括一些GCN變體。

　　該模型是一種靈活的模型，可以從多個方向進行擴充套件，為今後的研究提供了機會。例如，在我們的方法中，我們假設調節尋求重建和聚類之間的權衡的 $\alpha$ 係數等於1，研究這個值的選擇將是很有趣的。另一方面，雖然我們這項工作的重點是聚類，但值得將問題擴充套件到這樣的，例如，協同聚類，這在檔案聚類等許多現實場景中是有用的。

修改歷史

2022-06-27 建立文章

論文解讀目錄