分散式機器學習：同步並行SGD演演算法的實現與複雜度分析（PySpark）

1 分散式機器學習概述

大規模機器學習訓練常面臨計算量大、訓練資料大（單機存不下）、模型規模大的問題，對此分散式機器學習是一個很好的解決方案。

1）對於計算量大的問題，分散式多機並行運算可以基本解決。不過需要與傳統HPC中的共用記憶體式的多執行緒並行運算（如OpenMP）以及CPU-GPU計算架構做區分，這兩種單機的計算模式我們一般稱為計算並行）。

2）對於訓練資料大的問題，需要將資料進行劃分並分配到多個工作節點(Worker)上進行訓練，這種技巧一般被稱為資料並行。每個工作節點會根據區域性資料訓練出一個本地模型，並且會按照一定的規律和其他工作節點進行通訊（通訊內容主要是本地模型引數或者引數更新），以保證最終可以有效整合來自各個工作節點的訓練結果並得到全域性的機器學習模型。

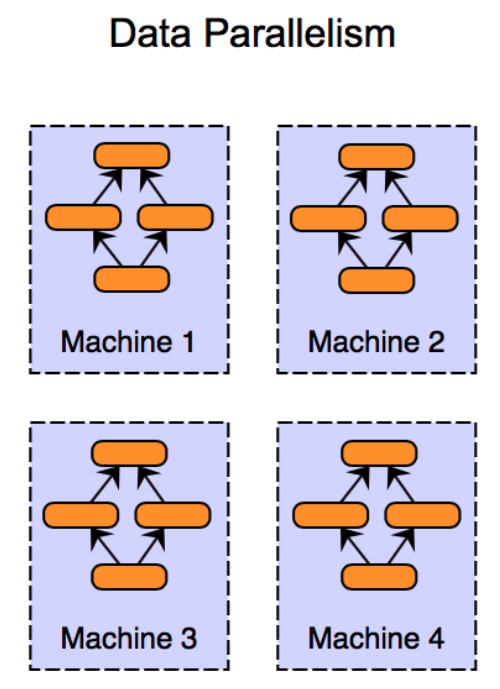
如果是訓練資料的樣本量比較大，則需要對資料按照樣本進行劃分，我們稱之為「資料樣本劃分」，按實現方法可分為「隨機取樣法」和「置亂切分法」。樣本劃分的合理性在於機器學習中的經驗風險函數關於樣本是可分的，我們將每個子集上的區域性梯度平均，仍可得到整個經驗風險函數的梯度。

如果訓練資料的維度較高，還可對資料按照維度進行劃分，我們稱之為「資料維度劃分」。它相較資料樣本劃分而言，與模型性質和優化方法的耦合度更高。如神經網路中各維度高度耦合，就難以採用此方式。不過，決策樹對維度的處理相對獨立可分，將資料按維度劃分後，各節點可獨立計算區域性維度子集中具有最優資訊增益的維度，然後進行彙總。此外，線上性模型中，模型引數與資料維度是一一對應的，故資料維度劃分常與下面提到的模型並行相互結合。

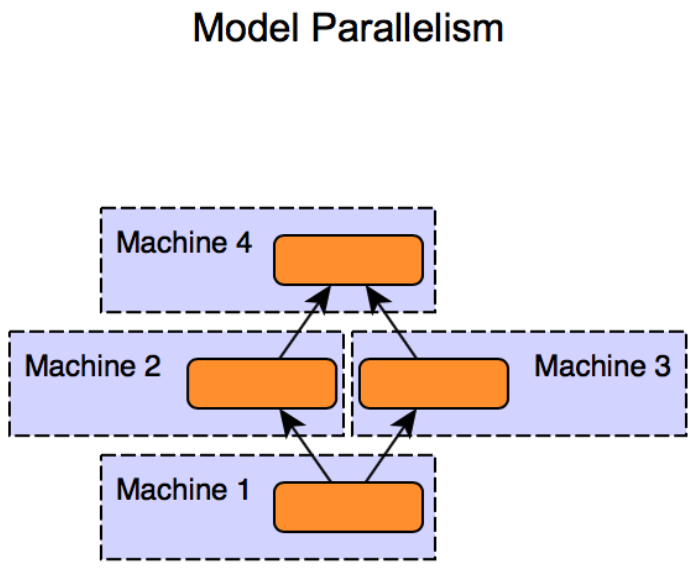
3）對於模型規模大的問題，則需要對模型進行劃分，並且分配到不同的工作節點上進行訓練，這種技巧一般被稱為模型並行。與資料並行不同，模型並行的框架下各個子模型之間的依賴關係非常強，因為某個子模型的輸出可能是另外一個子模型的輸入，如果不進行中間計算結果的通訊，則無法完成整個模型訓練。因此，一般而言，模型並行相比資料並行對通訊的要求更高。

這裡提一下資料樣本劃分中的幾種劃分方式。給定\(n\)個\(d\)維樣本和\(K\)個工作節點，資料樣本劃分需要完成的任務是將\(n\)個樣本以某種形式分配到\(K\)個工作節點上。

隨機取樣法中我們獨立同分布地從\(n\)個樣本中有放回隨機取樣，每抽取一個樣本將其分配到一個工作節點上。這個過程等價於先隨機採\(n\)個樣本，然後均等地劃分為\(K\)份。

隨機取樣法便於理論分析，但基於實現難度的考慮，在工程中更多采用的是基於置亂切分的劃分方法。即現將\(n\)個樣本隨機置亂，再把資料均等地切分為\(K\)份，再分配到\(K\)個節點上進行訓練。置亂切分相當於無放回取樣，每個樣本都會出現在某個工作節點上，每個工作節點的本地資料沒有重複，故訓練資料的資訊量一般會更大。我們下面的劃分方式都預設採取置亂切分的方法。

我們在後面的部落格中會依次介紹針對資料並行和模型並行設計的各種分散式演演算法。本篇文章我們先看資料並行中最常用的同步並行SGD演演算法（也稱SSGD）是如何在Spark平臺上實現的。

2 同步並行SGD演演算法描述與實現

SSGD^[1]對應的虛擬碼可以表述如下：

其中，SSGD演演算法每次依據來自\(K\)個不同的工作節點上的樣本的梯度來更新模型，設每個工作節點上的小批次大小為\(b\)，則該演演算法等價於批次大小為\(bK\)
的小批次隨機梯度下降法。

我們令\(f\)為邏輯迴歸問題的正則化經驗風險。設\(w\)為權值(最後一維為偏置)，樣本總數為\(n\)，\(\{(x_i, y_i)\}_{i=1}^n\)為訓練樣本集。樣本維度為\(d\)，\(x_i\in \mathbb{R}^{d+1}\)（最後一維擴充），\(y_i\in\{0, 1\}\)。則\(f\)表示為：

\[f(w) = \frac{1}{n} \sum_{i=1}^{n}\left[y_{i} \log \pi_{w}\left(x_{i}\right)+\left(1-y_{i}\right) \log \left(1-\pi_w\left(x_{i}\right)\right)\right] + \lambda R(w) \]

這裡

\[\begin{aligned} \pi_w(x) = p(y=1 \mid x; w) =\frac{1}{1+\exp \left(-w^{T} x\right)} \end{aligned} \]

其梯度表示如下：

\[\nabla f{(w)} = -\sum_{i=1}^n(y_i - \frac{1}{\exp(-w^Tx)+1})x_i + \lambda\nabla R(w) \]

這裡正則項的梯度\(\nabla R(w)\)要分情況討論：

(1) 不使用正則化

此時顯然\(\nabla R(w)=0\)。

(2) L2正則化(\(\frac{1}{2}\lVert w\rVert^2_2\))

此時\(\nabla R(w)=w\)。

(3) L1正則化(\(\lVert w \rVert_1\))

該函數不是在每個電都對\(w\)可導，只來採用函數的次梯度(subgradient)來進行梯度下降。\(\lVert w \rVert_1\)的一個比較好的次梯度估計是\(\text{sign}(w)\)。相比於標準的梯度下降，次梯度下降法不能保證每一輪迭代都使目標函數變小，所以其收斂速度較慢。

(4) Elastic net正則化(\(\alpha \lVert w \rVert_1 + (1-\alpha)\frac{1 }{2}\lVert w\rVert^2_2\))

對\(\lVert w\rVert_1\)使用次梯度計算式，\(\frac{1}{2}\lVert w\rVert_2^2\)使用其梯度計算式，得最終的梯度計算式為\(\alpha \text{sign}(w) + (1-\alpha) w\)。

我們約定計算第\(K\)個節點小批次\(\mathcal{I_k}\)的經驗風險的梯度\(\nabla f_{\mathcal{I_k}}(x)\)時不包含正則項的梯度，最終將\(K\)個節點聚合後再加上正則項梯度。

用PySpark對上述演演算法實現如下：

from sklearn.datasets import load_breast_cancer
import numpy as np
from pyspark.sql import SparkSession
from operator import add
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score

n_slices = 3  # Number of Slices
n_iterations = 300  # Number of iterations
eta = 10  # iteration step_size, because gradient sum is divided by minibatch size, it shoulder be larger
mini_batch_fraction = 0.1 # the fraction of mini batch sample 
lam = 0.001 # coefficient of regular term

def logistic_f(x, w):
    return 1 / (np.exp(-x.dot(w)) + 1)


def gradient(point: np.ndarray, w: np.ndarray):
    """ Compute linear regression gradient for a matrix of data points
    """
    y = point[-1]    # point label
    x = point[:-1]   # point coordinate
    # For each point (x, y), compute gradient function, then sum these up
    # notice thet we need to compute minibatch size, so return(g, 1)
    return - (y - logistic_f(x, w)) * x


def reg_gradient(w, reg_type="l2", alpha=0):
    """ gradient for reg_term
    """ 
    assert(reg_type in ["none", "l2", "l1", "elastic_net"])
    if reg_type == "none":
        return 0
    elif reg_type == "l2":
        return w
    elif reg_type == "l1":
        return np.sign(w)
    else:
        return alpha * np.sign(w) + (1 - alpha) * w
    

if __name__ == "__main__":

    X, y = load_breast_cancer(return_X_y=True)

    D = X.shape[1]
    X_train, X_test, y_train, y_test = train_test_split(
        X, y, test_size=0.3, random_state=0, shuffle=True)
    n_train, n_test = X_train.shape[0], X_test.shape[0]

    spark = SparkSession\
        .builder\
        .appName("SGD")\
        .getOrCreate()

    matrix = np.concatenate(
        [X_train, np.ones((n_train, 1)), y_train.reshape(-1, 1)], axis=1)

    points = spark.sparkContext.parallelize(matrix, n_slices).cache()

    # Initialize w to a random value
    w = 2 * np.random.ranf(size=D + 1) - 1
    print("Initial w: " + str(w))

    
    for t in range(n_iterations):
        print("On iteration %d" % (t + 1))
        w_br = spark.sparkContext.broadcast(w)
        
        (g, mini_batch_size) = points.sample(False, mini_batch_fraction, 42 + t)\
            .map(lambda point: gradient(point, w_br.value))\
            .treeAggregate(
                (0.0, 0),\
                    seqOp=lambda res, g: (res[0] + g, res[1] + 1),\
                        combOp=lambda res_1, res_2: (res_1[0] + res_2[0], res_1[1] + res_2[1])
            )

        w -= eta * g/mini_batch_size + lam * reg_gradient(w, "l2")
        
        y_pred = logistic_f(np.concatenate(
            [X_test, np.ones((n_test, 1))], axis=1), w)
        pred_label = np.where(y_pred < 0.5, 0, 1)
        acc = accuracy_score(y_test, pred_label)
        print("iterations: %d, accuracy: %f" % (t, acc))

    print("Final w: %s " % w)
    print("Final acc: %f" % acc)

    spark.stop()

我們嘗試以\(L2\)正則化、0.001的正則係數執行。初始權重如下：

Initial w: [ 0.09802896  0.92943671 -0.04964225  0.63915174 -0.61839489  0.86300117
 -0.04102299 -0.01428918  0.84966149  0.50712175  0.10373804 -0.00943291
  0.47526645 -0.19537069 -0.17958274  0.67767599  0.24612002  0.55646197
 -0.76646105  0.86061735  0.48894574  0.87838804  0.05519216 -0.14911865
  0.78695568  0.26498925  0.5789493  -0.20118555 -0.79919906 -0.79261251
 -0.77243226]

最終的模型權重與在測試集上的準確率結果如下：

Final w: [ 2.22381079e+03  4.00830646e+03  1.34874211e+04  1.38842558e+04
  2.19902064e+01  5.08904164e+00 -1.79005399e+01 -8.85669497e+00
  4.28643902e+01  1.74744234e+01  2.24167323e+00  2.89804554e+02
 -1.05612399e+01 -5.93151080e+03  1.60754311e+00  2.92290287e+00
  2.46318238e+00  1.51092034e+00  4.23645852e+00  1.38371670e+00
  2.20694252e+03  5.18743708e+03  1.32612364e+04 -1.39388946e+04
  3.03078787e+01  4.41094696e+00 -2.24172172e+01 -5.27976054e+00
  6.10623037e+01  1.83347648e+01  2.78974813e+02] 
Final acc: 0.912281

程式碼中有兩個關鍵點，一個是points.sample(False, mini_batch_fraction, 42 + t)。函數sample負責返回當前RDD的一個隨機取樣子集（包含所有分割區），其原型為：

RDD.sample(withReplacement: bool, fraction: float, seed: Optional[int] = None) → pyspark.rdd.RDD[T]

引數withReplacement的值為True表示取樣是有放回(with Replacement, 即replace when sampled out)，為False則表示無放回 (without Replacement)。如果是有放回，引數fraction表示每個樣本的期望被採次數，fraction必須要滿足\(\geqslant0\)；如果是無放回，引數fraction表示每個樣本被採的概率，fraction必須要滿足位於\([0, 1]\)區間內。

還有一個關鍵點是

.treeAggregate(
                (0.0, 0),\
                    seqOp=lambda res, g: (res[0] + g, res[1] + 1),\
                        combOp=lambda res_1, res_2: (res_1[0] + res_2[0], res_1[1] + res_2[1])
            )

該函數負責對RDD中的元素進行樹形聚合，它在資料量很大時比reduce更高效。該函數的原型為

RDD.treeAggregate(zeroValue: U, seqOp: Callable[[U, T], U], combOp: Callable[[U, U], U], depth: int = 2) → U[source]

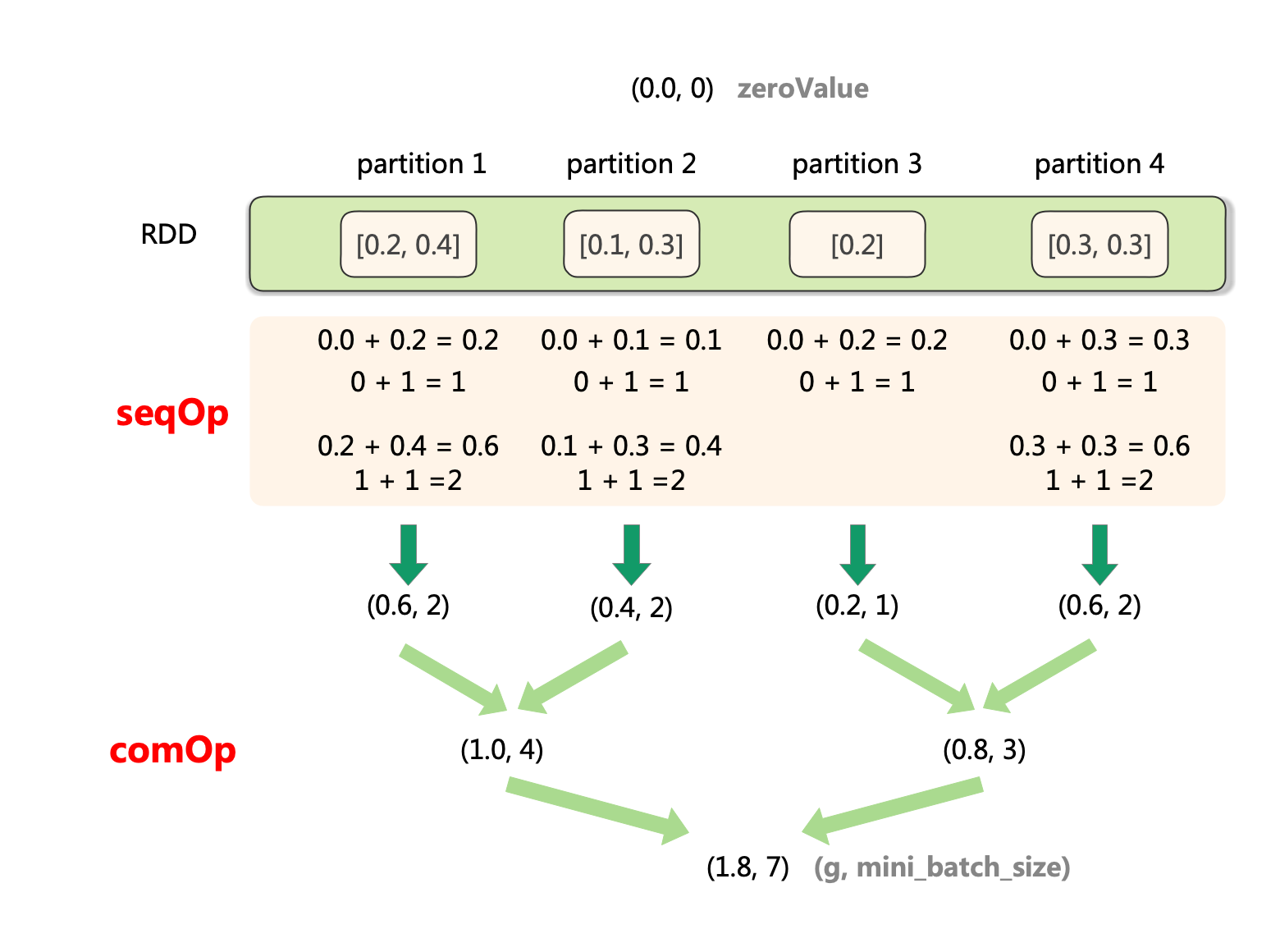
其中zeroValue為聚合結果的初始值，seqOp函數用於定義單分割區(partition)做聚合操作的方法，該方法第一個引數為聚合結果，第二個引數為分割區中的資料變數，返回更新後的聚合結果。combOp定義對分割區之間做聚合的方法，該方法第一個引數為第二個引數都為聚合結果，返回累加後的聚合結果。depth為聚合樹的深度。

我們這裡treeAggregate想要聚合得到一個元組(g, mini_batch_size)，g為所有節點樣本的隨機梯度和，mini_batch_size為所有節點所採的小批次樣本之和，故我們將聚合結果的初始值zeroVlue初始化為(0,0, 0)。具體的聚合過程描述如下：

對每個partition：
a. 初始化聚合結果為(0.0, 0)。
b. 對當前partition的序列元素，依次執行聚合操作seqOp。
c. 得到當前partition的聚合結果(partition_sum, partition_count)。
對所有partition：
a. 按照樹行模式合併各partition的聚合結果，合併方法為combOp。
b. 得到合併結果(total_sum, total_count)。

形象化地表示該聚合過程如下圖所示：

3 演演算法收斂性及複雜度分析

3.1 收斂性和計算複雜度

我們在部落格《數值優化：經典隨機優化演演算法及其收斂性與複雜度分析》中說過，假設目標函數\(f: \mathbb{R}^d\rightarrow \mathbb{R}\)是\(\alpha\)-強凸函數，並且\(\beta\)光滑，如果隨機梯度的二階矩有上界，即\(\mathbb{E}_{i^t}{\lVert\nabla f_{i^t}(w^t) \rVert^2\leqslant G^2}\)，當步長\(\eta^t = \frac{1}{\alpha t}\)時，對於給定的迭代步數\(T\)，SGD具有\(\mathcal{O}(\frac{1}{T})\)的次線性收斂速率：

\[\mathbb{E}[ f(w^T) - f(w^*) ] \leqslant \frac{2\beta G^2}{\alpha^2T} \]

而這意味著SGD的迭代次數複雜度為\(\mathcal{O}(\frac{1}{\varepsilon})\)，也即\(\mathcal{O}(\frac{1}{\varepsilon})\)輪迭代後會取得\(\varepsilon\)的精度。

儘管梯度的計算可以被分攤到個計算節點上，然而梯度下降的迭代是序列的。每輪迭代中，Spark會執行同步屏障(synchronization barrier)來確保在各worker開始下一輪迭代前\(w\)已被更新完畢。如果存在掉隊者(stragglers)，其它worker就會空閒(idle)等待，直到下一輪迭代。故相比梯度的計算，其迭代計算的「深度」(depth)是其計算瓶頸。

3.2 通訊複雜度

map過程顯然是並行的，並不需要通訊。broadcast過程需要一對多通訊，並且reduce過程需要多對一通訊（都按照樹形結構）。故對於每輪迭代，總通訊時間按

\[2\text{log}_2(p)(L + \frac{m}{B}) \]

增長。
這裡\(p\)為除去driver節點的運算節點個數，\(L\)是節點之間的通訊延遲。\(B\)是節點之間的通訊頻寬。\(M\)是每輪通訊中節點間傳輸的資訊大小。故訊息能夠夠以\(\mathcal{O}(\text{log}p)\)的通訊輪數在所有節點間傳遞。

參考

[1]
Zinkevich M, Weimer M, Li L, et al. Parallelized stochastic gradient descent[J]. Advances in neural information processing systems, 2010, 23.
[2] PySpark檔案：pyspark.RDD.sample函數
[3] PySpark檔案：pyspark.RDD.treeAggregate函數
[4] 劉浩洋，戶將等. 最佳化：建模、演演算法與理論[M]. 高教出版社, 2020.
[5] 劉鐵巖，陳薇等. 分散式機器學習：演演算法、理論與實踐[M]. 機械工業出版社, 2018.
[6] Stanford CME 323: Distributed Algorithms and Optimization (Lecture 7)