完美洗牌問題
作者:Grey
原文地址: 完美洗牌問題
問題描述
給定一個長度為偶數的陣列arr,假設長度為N*2
左部分:arr[L1...Ln]
右部分:arr[R1...Rn]
請把arr調整成arr[L1,R1,L2,R2,L3,R3,...,Ln,Rn]
要求時間複雜度O(N),額外空間複雜度O(1)
主要思路
解決完美洗牌問題之前,我們需要先解決另外一個相對簡單的演演算法問題:劍指 Offer 58 - II. 左旋轉字串
簡言之,如何原地讓一個陣列部分旋轉,比如:
[b,c,a,g,f,q]
我們需要讓區間[0...2]陣列和區間[3...5]的陣列進行旋轉,而且不能依賴輔助陣列,旋轉後的結果是
[g,f,q,b,c,a]
解決這個演演算法的思路是,首先,實現一個函數,反轉陣列
reverse(char[] arr, int l, int r)
這個函數的功能是將arr這個字串進行原地反轉,我們可以通過兩個指標來實現
public void reverse(char[] str, int l, int r) {
while (l < r) {
swap(str, l++, r--);
}
}
有了這個函數,我們可以先讓[0...2]區間先做reverse操作,然後再讓[3...5]區間做reverse操作,然後整體[0...5]做reverse操作,就實現了部分旋轉。
第一步,區間[0...2]做reverse操作,得到
[q,f,g,b,c,a]
第二步,區間[3...5]做reverse操作,得到
[q,f,g,a,c,b ]
第三步,區間[0...5]做reverse操作,得到
[b,c,a,g,f,q]
劍指 Offer 58 - II. 左旋轉字串完整程式碼如下
public class LeetCodeCN_0058_LCOF {
public String reverseLeftWords(String s, int n) {
char[] str = s.toCharArray();
rotate(str, 0, n - 1, s.length() - 1);
return String.valueOf(str);
}
public void rotate(char[] arr, int L, int M, int R) {
reverse(arr, L, M);
reverse(arr, M + 1, R);
reverse(arr, L, R);
}
public void reverse(char[] str, int l, int r) {
while (l < r) {
swap(str, l++, r--);
}
}
public void swap(char[] str, int l, int r) {
char tmp = str[l];
str[l] = str[r];
str[r] = tmp;
}
}
有了這個演演算法鋪墊,要解決完美洗牌問題,還需要推導一個公式,假設原陣列是

那麼經過洗牌後,要調整後的陣列是

通過觀察可知,對於原陣列任何一個位置i,在調整後的陣列應該位於j位置,其中i和j有如下關係,假設陣列長度為N,注:i和j都是從1開始算,而不是從0開始算
j = (2 * i) % (N + 1);
所以,針對上述陣列,遍歷每一個位置,都可以找到這個位置需要移動到的位置是哪裡,但是會出現一種情況,比如這個陣列,
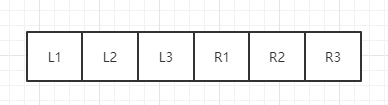
通過上述公式
L1頂替了L2的位置,把L2置換出來
L2被置換出來以後,頂替了R1的位置
R1被置換出來以後,頂替了L1的位置,此時,L1,L2,R1形成了一個環。
形成了如下情況
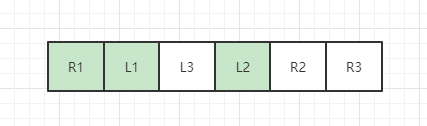
其中標綠的部分形成了一個環,我們還需要找到下一個未處理的位置,即L3位置,繼續呼叫上述公式,
通過上述公式
L3頂替了R3的位置,把R3置換出來
R3被置換出來以後,頂替了R2的位置
R2被置換出來以後,頂替了L3的位置,此時,L3,R2,R3形成了一個環。
形成了如下情況
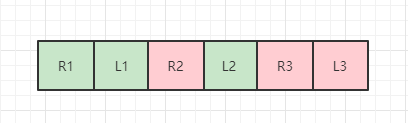
然後利用前面提到的部分陣列旋轉的方式,兩兩交換位置,得到最後的結果
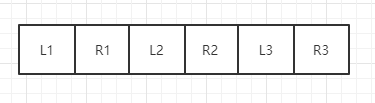
所以,針對這樣有環的情況,我們需要找到所有的入環點,然後依次呼叫公式,把元素放到正確的位置,在這裡,需要引入一個結論:
當陣列長度滿足N = 3^(k) - 1 的時候,環的出發點1,3,9...3^(k-1)
例如:
當陣列長度為8的時候,環的出發點分別是:1,3
當陣列長度為13的時候,環的出發點分別是:1,3,9
但是,陣列長度不滿足這個公式的時候,環的出發點就沒有這個規律,如果陣列長度不滿足這個公式,則需要獲取整個陣列離滿足這個公式最近的長度來進行操作,例如,陣列的長度為12,不滿足3^(k) - 1,

這個長度為12的陣列距離最近的一個滿足公式的位置是8(即:3^2 - 1),那麼可以將這個長度為12的陣列分成兩部分,一部分長度是8,另外一部分長度是4,

長度為8的陣列,應該是左邊四個(L1,L2,L3,L4),右邊四個(R1,R2,R3,R4),所以,我們對這個陣列做一次反轉,把區間[L5,L6]和區間[R1,R2,R3,R4]做一次反轉,得到

標紅部分,就可以通過公式得到入環點是L1和L3,然後利用入環點呼叫公式得到每個位置調整後的位置

剩餘長度為4的陣列,同樣找到離4最近的,滿足條件的長度是2(即:3^1 - 1), 然後將長度為4的陣列同樣做上述處理,得到
[外連圖片轉存失敗,源站可能有防盜鏈機制,建議將圖片儲存下來直接上傳(img-kFkhvSWa-1656092207194)(C:\Users\Young\AppData\Roaming\Typora\typora-user-images\image-20220625013014270.png)]
[L5,R5]這個陣列長度為2,滿足公式,帶入公式得到
[外連圖片轉存失敗,源站可能有防盜鏈機制,建議將圖片儲存下來直接上傳(img-Wh4wGhZk-1656092207194)(C:\Users\Young\AppData\Roaming\Typora\typora-user-images\image-20220625013129913.png)]
[L6,R6]同理,最後,得到如下陣列

並且將整個陣列兩兩交換,得到最終滿足條件的陣列

完整程式碼
public class LeetCode_1470_ShuffleTheArray {
public int[] shuffle(int[] arr, int n) {
shuffle(arr);
for (int i = 0; i < arr.length; i+=2) {
reverse(arr,i,i+1);
}
return arr;
}
public static void shuffle(int[] arr) {
if (arr == null || arr.length == 0 || (arr.length & 1) != 0) {
return;
}
shuffle(arr, 0, arr.length - 1);
}
public static void swap(int[] nums, int L, int R) {
if (nums == null || nums.length <= 1 || R == L) {
return;
}
nums[L] = nums[L] ^ nums[R];
nums[R] = nums[L] ^ nums[R];
nums[L] = nums[L] ^ nums[R];
}
public static void shuffle(int[] arr, int L, int R) {
while (R - L + 1 > 0) {
int len = R - L + 1;
int base = 3;
int k = 1;
while (base <= (len + 1) / 3) {
base *= 3;
k++;
}
int half = (base - 1) / 2;
int mid = (L + R) / 2;
rotate(arr, L + half, mid, mid + half);
toNext(arr, L, base - 1, k);
L = L + base - 1;
}
}
// i位置下一個位置應該去哪裡
// i 從1開始,而不是從0開始!!!
private static int findNextIndex(int i, int N) {
// return (2 * i) % (N + 1);
if (i <= N / 2) {
return 2 * i;
}
return (i - N / 2) * 2 - 1;
}
private static void toNext(int[] arr, int start, int len, int k) {
for (int i = 0, trigger = 1; i < k; i++, trigger *= 3) {
int pre = arr[start + trigger - 1];
int next = findNextIndex(trigger, len);
while (next != trigger) {
int t = arr[next + start - 1];
arr[next + start - 1] = pre;
pre = t;
next = findNextIndex(next, len);
}
arr[next + start - 1] = pre;
}
}
// @see LeetCodeCN_0058_LCOF
// L..M部分和M+1..R部分互換
public static void rotate(int[] arr, int L, int M, int R) {
reverse(arr, L, M);
reverse(arr, M + 1, R);
reverse(arr, L, R);
}
// L..R做逆序調整
public static void reverse(int[] arr, int L, int R) {
while (L < R) {
swap(arr, L++, R--);
}
}
}