帶你區分幾種並行
摘要:在實際應用中,影響並行加速比的因素主要是序列計算、平行計算和並行開銷三方面。
本文分享自華為雲社群《高效能運算(2)——萬丈高樓平地起》,作者: 我是一顆大西瓜。
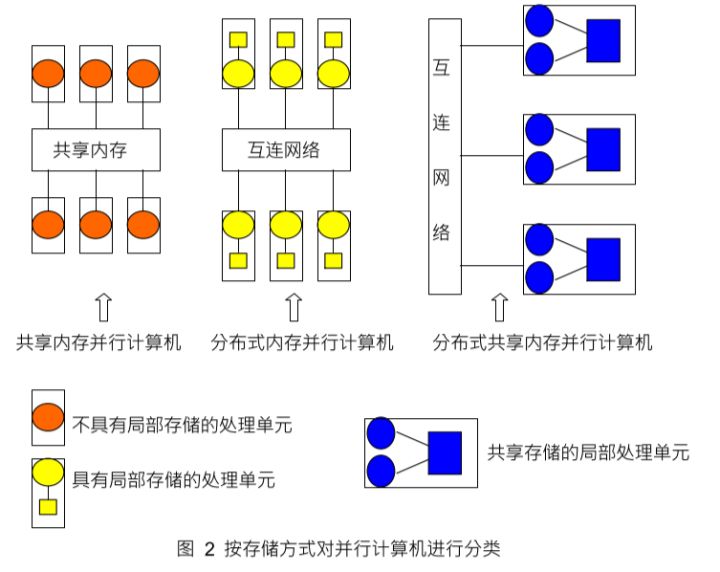
儲存方式
從物理劃分上共用記憶體和分散式記憶體是兩種基本的平行計算機儲存方式 除此之外分散式共用記憶體也是一種越來越重要的平行計算機儲存方式。
指令和資料
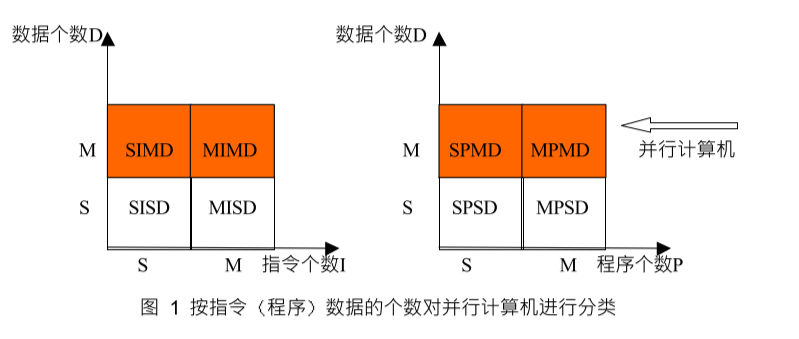
- [小粒度]根據一個平行計算機能夠同時執行的指令與處理資料的多少 可以把平行計算機分為 SIMD Single-Instruction Multiple-Data 單指令多資料平行計算機和MIMD Multiple-Instruction Multiple-Data 多指令多資料平行計算機
- [大粒度]按同時執行的程式和資料的不同 又提出了SPMD Single-Program Multuple-Data 單程式多資料平行計算機和MPMD Multiple-ProgramMultiple-Data 多程式多資料平行計算機
根據指令的同時執行和資料的同時執行,計算機系統可以分成以下四類:
- 單處理器,單資料 (SISD)
- 單處理器,多資料 (SIMD)
- 多處理器,單資料 (MISD)
- 多處理器,多資料 (MIMD)
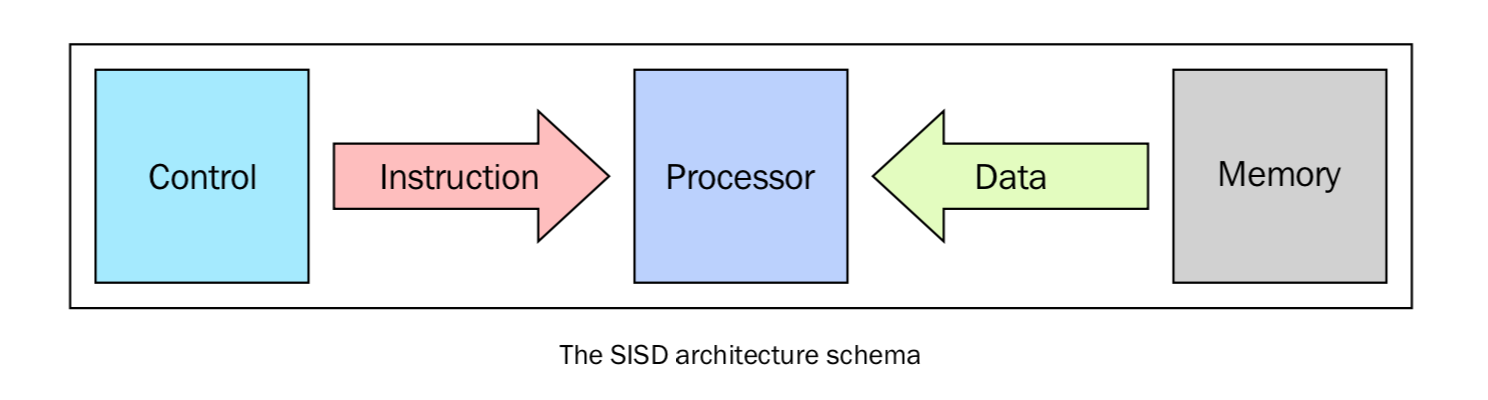
SISD
單處理器單資料就是「單CPU的機器」,它在單一的資料流上執行指令。在SISD中,指令被順序地執行。
對於每一個「CPU時鐘」,CPU按照下面的順序執行:
- Fetch: CPU 從一片記憶體區域中(暫存器)獲得資料和指令
- Decode: CPU對指令進行解碼
- Execute: 該執行在資料上執行,將結果儲存在另一個暫存器中
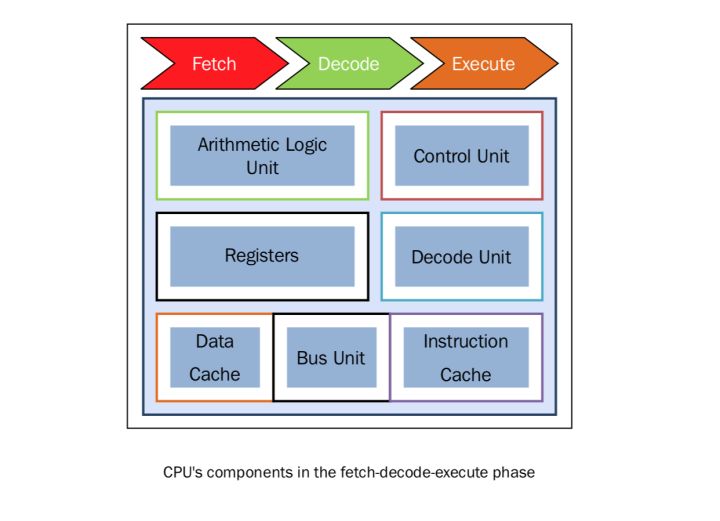
這種架構(馮·諾依曼體系)的主要元素有以下:
- 中心記憶體單元:儲存指令和資料
- CPU:用於從記憶體單元獲得指令/資料,對指令解碼並順序執行它們
- I/O系統:程式的輸入和輸出流
傳統的單處理器計算機都是經典的SISD系統。下圖表述了CPU在Fetch、Decode、Execute的步驟中分別用到了哪些單元:
MISD
這種模型中,有n個處理器,每一個都有自己的控制單元,共用同一個記憶體單元。在每一個CPU時鐘中,從記憶體獲得的資料會被所有的處理器同時處理,每一個處理器按照自己的控制單元傳送的指令處理。在這種情況下,並行實際上是指令層面的並行,多個指令在相同的資料上操作。能夠合理利用這種架構的問題模型比較特殊,例如資料加密等。因此,MISD在現實中並沒有很多用武之地,更多的是作為一個抽象模型的存在。
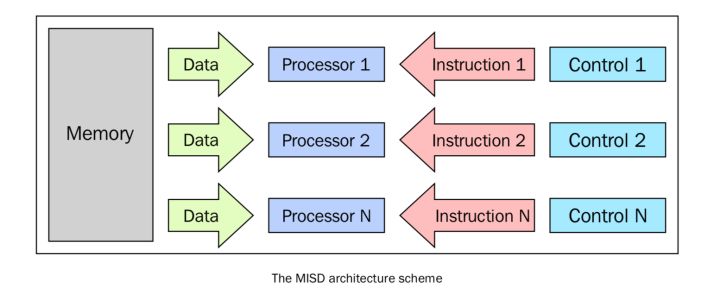
SIMD
SIMD計算機包括多個獨立的處理器,每一個都有自己的區域性記憶體,可以用來儲存資料。所有的處理器都在單一指令流下工作;具體說,就是有n個資料流,每個處理器處理一個。所有的處理器同時處理每一步,在不同的資料上執行相同的指令。
很多問題都可以用SIMD計算機的架構來解決。這種架構另一個有趣的特性是,這種架構的演演算法非常好設計,分析和實現。限制是,只有可以被分解成很多個小問題(小問題之間要獨立,可以不分先後順序被相同的指令執行)的問題才可以用這種架構解決。很多超級計算機就是使用這架構設計出來的。例如Connection Machine(1985年的 Thinking Machine)和MPP(NASA-1983).我們在第六章 GPU Python程式設計中會接觸到高階的現代圖形處理器(GPU),這種處理器就是內建了很多個SIMD處理單元,使這種架構在今天應用非常廣泛。
MIMD
在費林分類中,這種計算機是最廣泛使用、也是最強大的一個種類。這種架構有n個處理器,n個指令流,n個資料流。每一個處理器都有自己的控制單元和區域性記憶體,讓MIMD架構比SIMD架構的計算能力更強。每一個處理器都在獨立的控制單元分配的指令流下工作;因此,處理器可以在不同的資料上執行不同的程式,這樣可以解決完全不同的子問題甚至是單一的大問題。在MIMD中,架構是通過執行緒或程序層面的並行來實現的,這也意味著處理器一般是非同步工作的。這種型別的計算機通常用來解決那些沒有統一結構、無法用SIMD來解決的問題。如今,很多計算機都應用了這中間架構,例如超級計算機,計算機網路等。然而,有一個問題不得不考慮:非同步的演演算法非常難設計、分析和實現。
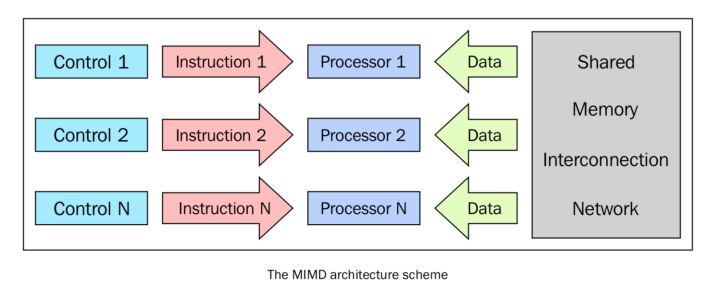
並行和並行
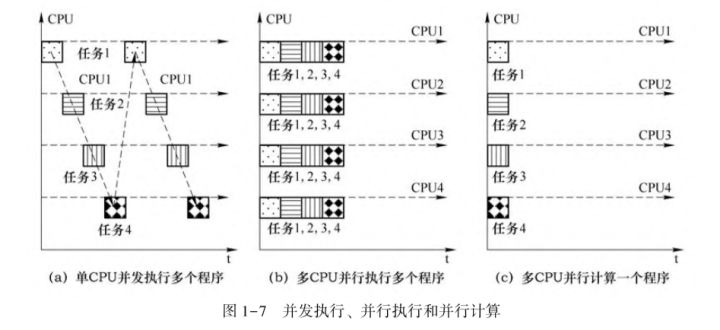
並行型別
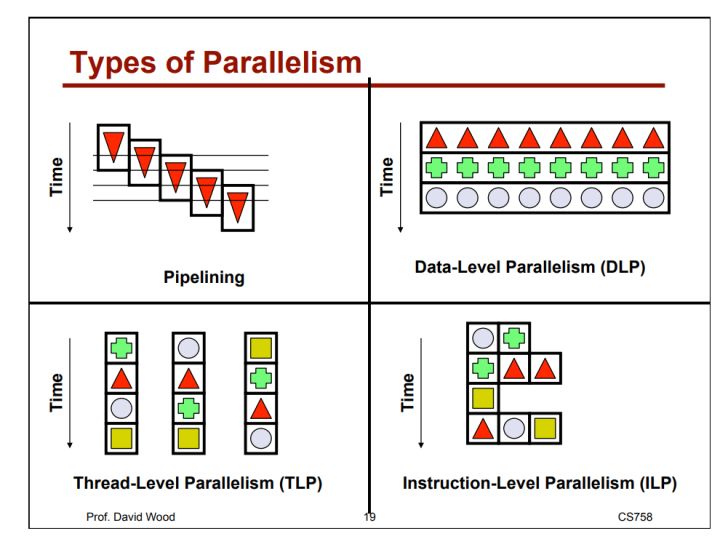
幾種並行區分

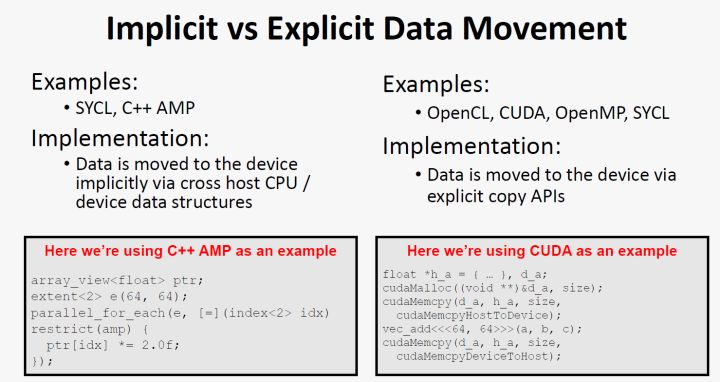

程式、執行緒、程序和超執行緒
- 程式程式是一組指令的有序集合。它本身沒有任何執行的含義,只是存在於計算機系統的硬碟等儲存空間中一個靜態的實體檔案。比如Linux系統下的binary excutable,windows系統下的exe
- 程序程序是處於動態條件下由作業系統維護的系統資源管理實體。程序具有自己的生命週期, 反映了一個程式在一定的資料集上執行的全部動態過程。需要載入到記憶體中,點開一個exe就是開啟了一個程序
- 執行緒。執行緒則是程序的一個實體,是比程序更小的能獨立執行的基本單位,是被系統排程和分配的基本單元。執行緒自身基本上不擁有系統資源,只擁有一點在執行中必不可少的資源 (如程式計數器、一組暫存器和呼叫堆疊), 但它與同屬一個程序的其他執行緒共用所屬程序所擁有的全部資源,同一個程序的多個執行緒可以並行執行,從而提高了系統資源的利用率
- 超執行緒超執行緒技術就是利用特殊的硬體指令,把兩個邏輯核心模擬成兩個物理晶片,讓單顆CPU都能進行執行緒級平行計算,進而相容多執行緒作業系統和軟體。一般一個CPU對應一個執行緒,通過超執行緒可以達到比如8核16執行緒
老生常談,執行緒和程序的區別和聯絡:
- 一個程式的執行至少有一個程序,一個程序至少包含一個執行緒(主執行緒)。
- 執行緒的劃分尺度小於程序,所以多執行緒程式並行性更高。
- 程序是系統進行資源分配和排程的一個獨立單位,執行緒是CPU排程和分派的基本單位。同一程序內允許多個執行緒共用其資源。
- 程序擁有獨立的記憶體單元,即程序之間相互獨立;同一程序內多個執行緒共用記憶體。因此,執行緒間能通過讀寫操作對它們都可見的記憶體進行通訊,而程序間的相互通訊則需要藉助於訊息的傳遞。
- 每個執行緒都有一個程式執行的入口,順序執行序列和程式執行的出口,但執行緒不能單獨執行,必須依存於程序中,由程序控制多個執行緒的執行
- 程序比執行緒擁有更多的相應狀態,所以建立或銷燬程序的開銷要比建立或銷燬執行緒的開銷大得多。因此,程序存在的時間長,而執行緒則隨著計算的進行不斷地動態地派生和縮並。
- 一個執行緒可以建立和復原另一個執行緒。而且同一程序中的多個執行緒共用所屬程序所擁有的全部資源;同時程序之間也可以並行執行,從而更好地改善了系統資源的利用率。
執行緒繫結
計算機系統是由一個或多個物理處理器和記憶體組成,執行的程式會將記憶體分為兩個部分,一部分是共用變數使用的儲存區域, 另一部分供各執行緒的私有變數使用的儲存區域。執行緒繫結是將執行緒繫結在固定的處理器上, 從而線上程與處理器之間建立一對一的對映關係。如果不進行執行緒繫結,執行緒可能在不同的時間片執行在不同的處理器上。我們知道,每個處理器是有自己的多級快取的,如果執行緒切來切去,那麼cache命中率肯定不高,程式效能也會受到影響。通過執行緒繫結,程式能夠獲得更高的cache利用率從而提高程式效能。c++中如何進行執行緒繫結可以參考https://www.cnblogs.com/wenqiang/p/6049978.html

並行演演算法評價
理論上來說,n個相同的cpu理論上能提供n倍的計算能力。
但是在實際過程中,並行開銷會導致總的執行時間無法線性地減少。這些開銷分別為:
- 執行緒的建立和銷燬、 執行緒和執行緒之間的通訊、 執行緒間的同步等因素造成的開銷。
- 存在不能並行化的計算程式碼,造成計算由單個執行緒完成, 而其他執行緒則處於閒置狀態。
- 為爭奪共用資源而引起的競爭造成的開銷。
- 由於各cpu工作負載分配的不均衡和記憶體頻寬等因素的限制,一個或多個執行緒由於缺少工作或因為等待特定事件的發生無法繼續執行而處於空閒狀態。
並行加速比(加速比)
加速比的定義是順序程式執行時間除以計算同一結果的並行程式的執行時間
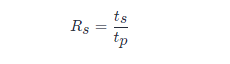
式中,t_sts為一顆CPU程式完成該任務所需序列執行時間;t_ptp為n顆CPU並行執行完成該任務所需時間。由於序列執行時間t_sts為n顆CPU並行執行完成該 和並行執行時間t_ptp有多種定義方式。 這樣就產生了五種不同的加速比的定義,即相對加速比、實際加速比、絕對加速比、漸近實際加速比和漸近相對加速比。
並行效率(效率)
在實際應用中,影響並行加速比的因素主要是序列計算、平行計算和並行開銷三方面。一般情況下, 並行加速比小於CPU的數量。但是,有時會出現一種奇怪的現象,即並行程式能以序列程式快n倍的速度執行,稱為超線性加速比。產生超線性加速的原因在於CPU存取的資料都駐留在各自的快取記憶體Cache中, 而快取記憶體的容量比記憶體要小, 但讀寫速度卻遠高於記憶體。
衡量並行演演算法的另一個主要標準是並行效率,它表示的是多顆CPU在進行平行計算時單顆CPU的平均加速比。
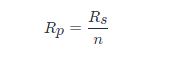
理想並行效率為1表明全部CPU都在滿負荷工作。通常情況下,並行效率會小於1, 且隨CPU數量的增加而減小。
伸縮性
伸縮性用於度量並行機器高效執行的能力,代表跟處理器數量成比例的計算能力 (執行速度)。如果問題的規模和處理器的數量同時增加,效能不會下降。
阿姆德爾定律 (Ahmdal’s law)
阿姆德爾定律廣泛使用於處理器設計和並行演演算法設計。它指出程式能達到的最大加速比被程式的序列部分限制。$S=1/(1-p) $中 1-p1−p 指程式的序列部分。它的意思是,例如一個程式90%的程式碼都是並行的,但仍存在10%的序列程式碼,那麼系統中即使由無限個處理器能達到的最大加速比仍為9。
古斯塔夫森定律 (Gustafson’s law)
古斯塔夫森定律在考慮下面的情況之後得出的:
- 當問題的規模增大時,程式的序列部分保持不變。
- 當增加處理器的數量時,每個處理器執行的任務仍然相同。
古斯塔夫森定律指出了加速比S(P)=P-\alpha (P-1)S(P)=P−α(P−1), PP 為處理器的數量, SS 為加速比,\alphaα 是並行處理器中的非並行的部分。作為對比,阿姆德爾定律將單個處理器的執行時間作為定量跟並行執行時間相比。因此阿姆德爾定律是基於固定的問題規模提出的,它假設程式的整體工作量不會隨著機器規模 (也就是處理器數量) 而改變。古斯塔夫森定律補充了阿姆德爾定律沒有考慮解決問題所需的資源總量的不足。古斯塔夫森定律解決了這個問題, 它表明設定並行解決方案所允許耗費的時間的最佳方式是考慮所有的計算資源和基於這類資訊。