論文資訊

論文標題：Towards Explanation for Unsupervised Graph-Level Representation Learning
論文作者：Qinghua Zheng, Jihong Wang, Minnan Luo, Yaoliang Yu, Jundong Li, Lina Yao, Xiaojun Chang
論文來源：2022, arXiv
論文地址：download 
論文程式碼：download

1 Introduction

　　使用資訊瓶頸的圖級表示可解釋性。

2 Notations and preliminaries

2.1 Information Bottleneck

　　給定輸入資料 $X$ 及其標籤 $Y$，Information Bottleneck 的目的是發現一個壓縮的潛在表示 $Z$，它以 $Y$ 提供最大的資訊。在形式上，我們可以通過優化以下優化問題來學習潛在的表示 $Z$：

　　　　$\underset{Z}{max } \;\mathcal{L}_{I B}=I(Z ; Y)-\beta I(X ; Z)\quad\quad\quad(1)$

　　其中，$\beta$ 表示對資訊量和壓縮量的超引數權衡。

　　互資訊(MI)I（X；Z）度量兩個隨機變數的相關性，表述為

　　　　$I(X ; Z)= \int_{x} \int_{z} p(x, z) \log \frac{p(x, z)}{p(x) p(z)} d x d z $

2.2 GNN explanation

　　GNN的解釋旨在理解對GNN的計算過程至關重要的圖的內在資訊，從而提供人類可理解的解釋。具體來說，給定一個圖 $G$ 和一個學習條件分佈 $P_{\psi}(\hat{Z} \mid G), \mathrm{GNN}$ 的GNN模型 $\psi$)，GNN解釋的目的是學習與GNN的計算結果最相關的解釋子圖 $S$，即：

　　　　$\underset{S \in \mathcal{S}}{\text{arg max }}  \operatorname{Score}(S, \hat{Z})\quad\quad\quad(2)$

　　其中，$\mathcal{S}$ 表示由圖 $G$ 的所有可能的子圖組成的集合；$\operatorname{Score}(S, \hat{Z})$ 測量了子圖 $\mathcal{S}$ 和 GNN 的計算結果 $\hat{Z}$ 之間的相關性。

　　例如，GNNExcraner[9]關注於對監督 GNN 的解釋，並將相關評分 $\operatorname{Score}(S, \hat{Z})$ 形式化為互資訊，即

　　　　$S=\arg \max _{S \in \mathcal{S}} I(S ; \hat{Y})$

　　其中，隨機變數 $\hat{Y}=\hat{Z}$ 表示分類概率。

3 Method

3.1 Unsupervised Subgraph Information Bottleneck

　　在本文中，我們研究了無監督圖級表示學習的未探索的解釋問題。給定一個由無監督 GNN 提取的圖 $G$ 及其對應的表示 $Z$，我們的目標是識別與這些表示最相關的解釋子圖 $S$。

　　根據前面的解釋工作原理[9,10]，我們利用互資訊來度量相關性，因此將解釋問題表述為 $\underset{S}{\text{arg max }} I(S ; Z)$。不幸的是，由於 $I(Z ; S) \leq I(Z ; G)$(證明見附錄B)，因此已經證明了存在一個平凡的解 $S=G$。瑣碎的解決方案表明，解釋子圖年代可能包含多餘的資訊，例如，噪聲和無關的資訊表示 $Z$ 受 $IB$ 原則的成功解釋監督網路[19]，我們推廣 $IB$ 原則無監督設定，以避免瑣碎的解決方案和利用一個新的原則。

　　Definition. (Unsupervised Subgraph Information Bottleneck: USIB). Given a graph $G$ and its representation $Z$ , the USIB seeks for the most informative yet compressed explanation $S$ through optimization problem

　　　　$ \underset{S}{\text{max } }\mathcal{L}_{U S I B}=I(Z ; S)-\beta I(G ; S)\quad\quad\quad(3)$

　　通過優化USIB目標，我們可以在解釋性子圖的資訊性和壓縮性之間進行權衡。然而，由於USIB目標的優化，互資訊涉及到高維資料的積分，這是非常困難的。因此，需要利用互資訊估計方法。

3.2 Optimization for USIB

　　我們分別在USIB的目標中處理兩項 $I(Z ; S)$ 和 $I(G ; S)$。

Maximizing $I(Z ; S)$

　　我們採用 Jensen-Shannon MI estimator [32,33]來為 $I(Z；S)$ 分配一個近似的下界，即，

　　　　$\hat{I}^{J S D}(Z ; S):=\sup _{f_{\phi}} \mathbb{E}_{p(S, Z)}\left[-s p\left(-f_{\phi}(S, Z)\right)\right]-\mathbb{E}_{p(S), p(Z)}\left[s p\left(f_{\phi}(S, Z)\right)\right]\quad\quad\quad(4)$

　　其中 $ s p(x)=\log \left(1+e^{x}\right)$ 為 softplus function；函數 $ f_{\phi}: \mathcal{S} \times \mathcal{Z} \rightarrow \mathbb{R}$ 是帶可學習引數 $\phi $，以區分 $S$ 和 $Z$ 的範例是否從聯合分佈中取樣。它是由 $\mathrm{MLP}_{\phi_{1}}$ 和 $\mathrm{GNN}_{\phi_{2}}$ 的函數複合來實現的，即：

　　　　$f_{\phi}\left(S^{(k)}, Z^{(k)}\right)=\operatorname{MLP}_{\phi_{1}}\left(\operatorname{GNN}_{\phi_{2}}\left(S^{(k)}\right) \| Z^{(k)}\right)\quad\quad\quad(5)$

　　其中，$\phi=\left\{\phi_{1}, \phi_{2}\right\}$；$\|$ 是指連線操作符。請注意，先驗分佈 $p(S, Z)$ 和 $p(Z)$ 在實踐中通常是不可到達的。結合蒙特卡羅抽樣來近似先驗分佈，我們得到了一個近似下界 $Eq.4$ 由：

　　　　$\underset{\phi}{max} \mathcal{L}_{1}(\phi, S)=\frac{1}{K} \sum\limits_{k=1}^{K}-s p\left(-f_{\phi}\left(S^{(k)}, Z^{(k)}\right)\right)-\frac{1}{K} \sum\limits_{k=1, m \neq k}^{K} s p\left(f_{\phi}\left(S^{(k)}, Z^{(m)}\right)\right)\quad\quad\quad(6)$

　　其中，$K$ 為樣本的數量。$\left(S^{(k)}, Z^{(k)}\right)$ 從聯合分佈 $p(S, Z)$ 中取樣，$\left(S^{(k)}, Z^{(m)}\right)$ 分別從邊緣分佈 $p(S)$ 和 $p(Z)$ 中獨立取樣。在實踐中，我們通過隨機排列從聯合分佈中抽樣 $\left(S^{(k)}, Z^{(k)}\right)$ 對來取樣 $\left(S^{(k)}, Z^{(m)}\right)$。

Minimizing $\boldsymbol{I}(\boldsymbol{G} ; \boldsymbol{S}) $

　　請注意，解釋子圖的熵 $H(S)=\mathbb{E}_{p(S)}[-\log p(S)]$ 為 $I(G ; S)$ 提供了一個上界，因為不等式 $I(G ; S)=H(S)-H(S \mid G) \leq H(S)$ 成立。然而，由於在實踐中 $S$ 的先驗分佈未知的，因此很難計算熵。為了解決這個問題，我們考慮一個鬆弛，並假設解釋圖是一個吉爾伯特隨機圖(Gilbert random graph)[34]，其中邊有條件地相互獨立。具體地說，讓 $(i, j) \in \mathcal{E}$ 表示圖 $G$ 的邊，$e_{i, j} \sim \operatorname{Bernoulli}\left(\mu_{i, j}\right)$ 是一個二元變數指示是否為子圖 $S$ 選擇邊 $(i, j)$ 。因此，子圖的概率分解為 $p(S)=\prod\limits _{(i, j) \in \mathcal{E}} p\left(e_{i, j}\right)$，其中 $p\left(e_{i, j}\right)=\mu_{i, j}^{e_{i, j}}\left(1-\mu_{i, j}\right)^{1-e_{i, j}}$。這樣，我們就可以用蒙特卡羅抽樣得到 $I(G ; S)$ 的一個近似上界，它記為

　　　　$\mathcal{L}_{2}(S)=-\frac{1}{K} \sum\limits_{k=1}^{K} \sum\limits_{(i, j) \in \mathcal{E}} e_{i, j}^{(k)} \log \mu_{i, j}^{(k)}+\left(1-e_{i, j}^{(k)}\right) \log \left(1-\mu_{i, j}^{(k)}\right)\quad\quad\quad(7)$

　　基於梯度的優化方法可能無法優化 $\text{Eq.6}$ 和 $\text{Eq.7}$ ，由於不可微取樣過程和子圖結構的離散性質。因此，我們遵循 Gumbel-Softmax reparametrization trick [35, 36] 並將二元變數 $e_{i, j}$ 放寬為一個連續的邊權值變數 $\hat{e}_{i, j}=\sigma((\log \epsilon-\log (1-\epsilon)+ \left.\left.w_{i, j}\right) / \tau\right) \in[0,1]$，其中 $\sigma(\cdot)$ 是 sigmoid function ；$\epsilon \sim \operatorname{Uniform}(0,1)$；$\tau$ 是溫度超引數，並有 $\lim _{\tau \rightarrow 0} p\left(\hat{e}_{i, j}=1\right)=\sigma\left(w_{i, j}\right)$；$w_{i, j}$ 是由神經網路根據之前的工作計算的潛在變數:

　　　　$w_{i, j}^{(k)}=\operatorname{MLP}_{\theta_{1}}\left(\mathbf{z}_{i}^{(k)} \| \mathbf{z}_{j}^{(k)}\right) \text { with } \mathbf{z}_{i}^{(k)}=\operatorname{GNN}_{\theta_{2}}\left(G^{(k)}, i\right), i=1,2, \cdots\quad\quad\quad(8)$

　　其中，$\mathbf{z}_{i}^{(k)}$ 表示節點 $i$ 的節點表示。為了更好地表示，我們表示 $\theta=   \left\{\theta_{1}, \theta_{2}\right\}$，並通過 $\hat{S}^{(k)}=g_{\theta}\left(G^{(k)}\right)^{3}$ 生成鬆弛子圖 $\hat{S}$。設 $\mu_{i, j}^{(k)}=\sigma\left(w_{i, j}^{(k)}\right)$，等式中的 $\text{Eq.7}$ 可以被重寫為

　　　　$\mathcal{L}_{2}\left(g_{\theta}\left(G^{(k)}\right)\right)=-\frac{1}{K} \sum\limits_{k=1}^{K} \sum\limits_{(i, j) \in \mathcal{E}} \hat{e}_{i, j}^{(k)} \log \sigma\left(w_{i, j}^{(k)}\right)+\left(1-\hat{e}_{i, j}^{(k)}\right) \log \left(1-\sigma\left(w_{i, j}^{(k)}\right)\right)\quad\quad\quad(9)$

　　總之，我們重寫了USIB優化問題 $\text{Eq.3}$ 作為：

　　　　$\underset{\phi, \theta}{\text{max }} \mathcal{L}_{U S I B}(\phi, \theta, G)=\mathcal{L}_{1}\left(\phi, g_{\theta}\left(G^{(k)}\right)\right)-\beta * \mathcal{L}_{2}\left(g_{\theta}\left(G^{(k)}\right)\right)\quad\quad\quad(10)$

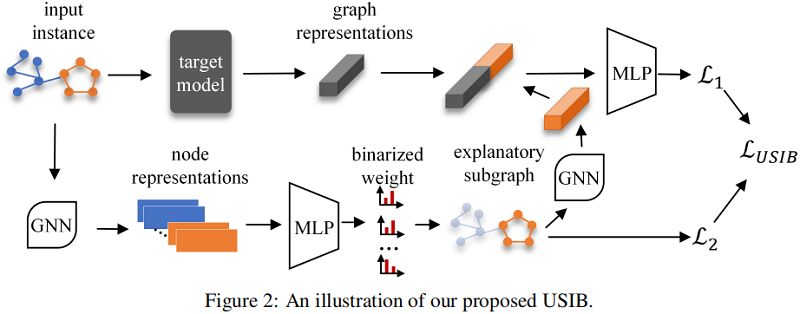
　　我們的方法的概述如 Fig. 2 所示。首先通過神經網路生成解釋子圖，然後利用另一個網路來估計解釋子圖和圖表示之間的互資訊。最後，對子圖生成器和互資訊估計器進行了協同優化。最終的解釋性子圖可以通過選擇具有 top-n 個邊權值 $\left(\hat{e}_{i, j}^{(k)}\right)$ 的邊來實現。詳細的演演算法可以在附錄中找到。

　　

3 Experiments

　　在本節中，我們通過回答以下問題來實證評估我們所提出的方法的有效性和優越性。

• RQ1 How does our proposed method perform compared to other baseline explainers?
• RQ2 Does expressiveness and robustness of representations affect the fifidelity of explanatory subgraphs in agreement with the theoretical analysis?

　　

　　

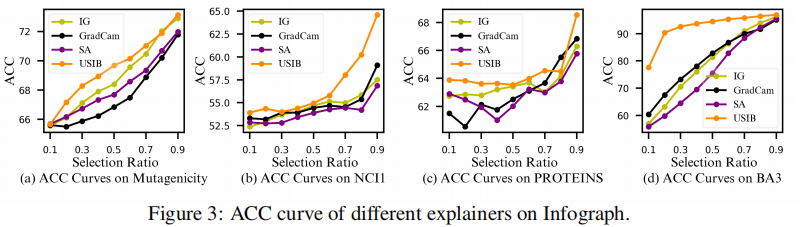
3.2 Inflfluence of representations’ expressiveness and robustness

　　

4 Conclusion

　　我們研究了一個未被探索的解釋問題：對無監督圖表示學習的解釋。我們提出了IB原理來解決解釋問題，從而產生了一種新的解釋方法USIB。此外，我們還從理論上分析了標籤空間上的表示和解釋子圖之間的聯絡，結果表明，表達性和魯棒性有利於解釋子圖的保真度。在四個資料集和三個目標模型上的廣泛結果證明了我們的方法的優越性和理論分析的有效性。作為未來的研究方向，我們考慮了無監督表示學習的反事實解釋[42]，並探討了解釋和對抗性例子[43,44,45]之間是否存在聯絡。

 

 

修改歷史

2022-06-21 建立文章

 

論文解讀目錄

 

參考文獻

圖論——隨機圖與隨機點積圖