程式分析與優化
本章是系列文章的第七章,終於來到了鼎鼎大名的SSA,SSA是編譯器領域最偉大的發明之一,也是影響最廣的發明。
本文中的所有內容來自學習DCC888的學習筆記或者自己理解的整理,如需轉載請註明出處。周榮華@燧原科技
7.1 控制流圖回顧
對下面的c程式碼儲存成7.1.cc:
1 int max(int a, int b) { 2 int ans = a; 3 if (b > a) { 4 ans = b; 5 } 6 return ans; 7 }
直接用clang生成bc → dot → svg,最終svg的結果如下:
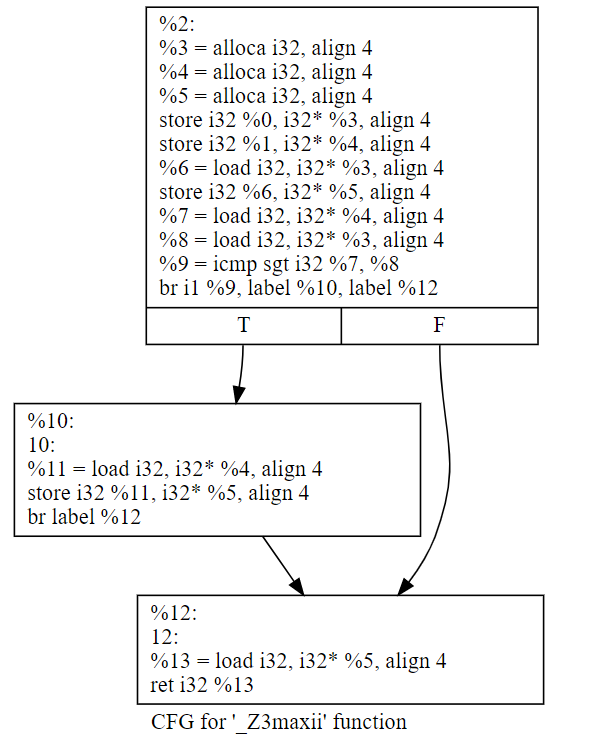
如果經過一輪opt的優化「opt -mem2reg 7.1.ll -o 7.1.1.bc」之後的結果,就變成了這樣(注意,需要刪除ll裡面的optnone屬性,否則opt不會生效):
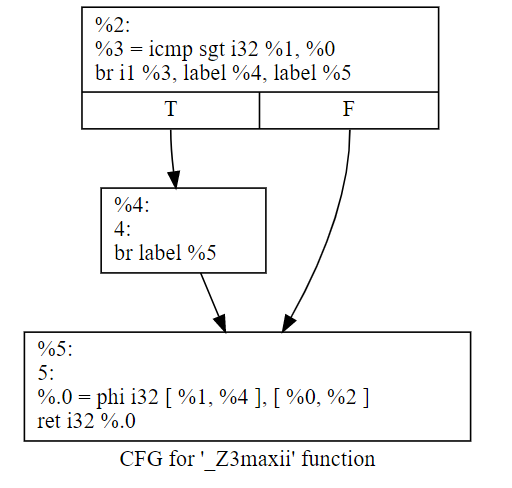
除了我們本來準備跑的mem2reg的pass外,優化前後最後一個BB裡是不是還多了一個phi函數?
7.1.1 靜態單賦值正規化(SSA Form)
靜態單賦值,字面意思是對靜態的變數只有一次賦值點。這是現在所有編譯器都廣泛使用的屬性,也是編譯器歷史上最具有突破性意義的屬性,簡化了各種分析和優化的過程。
1991年SSA的奠基論文被參照打到2800+次,這還是截止2019年的資料,這個參照次數每年還在增加。
幾乎每本講編譯器的書都會說到SSA。google學術上用SSA能搜到5000+個結果。
每年來自全世界的編譯器專家,都會在SSA研討會上慶祝一次SSA的誕生。
和靜態單賦值對應的是動態單賦值,也就是程式執行過程中,每個變數只能賦值一次。和動態單賦值不同,靜態單賦值,只要求每個變數的賦值程式點只能有一個,這個程式點可以出現在迴圈內部(這意味著動態執行過程中這個程式點會多次執行)。
7.2 從SSA來到SSA去
7.2.1 將線性程式碼轉換成SSA Form
如果一個程式沒有任何分叉,則稱這個程式是線性程式碼。
例如下面的程式碼:
1 double baskhara(double a, double b, double c) { 2 double delta = b * b - 4 * a * c; 3 double sqrDelta = sqrt(delta); 4 double root = (b + sqrDelta) / 2 * a; 5 return root; 6 }
其實它本身就是符合SSA定義的(每個變數只定義一次),但一般經過opt轉換之後的程式碼是這樣:
1 define double @baskhara(double %a, double %b, double %c) { 2 %1 = fmul double %b, %b 3 %2 = fmul double 4.000000e+00, %a 4 %3 = fmul double %2, %c 5 %4 = fsub double %1, %3 6 %5 = call double @sqrt(double %4) 7 %6 = fadd double %b, %5 8 %7 = fdiv double %6, 2.000000e+00 9 %8 = fmul double %7, %a 10 ret double %8 11 }
線性程式碼轉換成SSA正規化的的演演算法比較直接:
1 for each variable a: 2 Count[a] = 0 3 Stack[a] = [0] 4 rename_basic_block(B) = 5 for each instruction S in block B: 6 for each use of a variable x in S: 7 i = top(Stack[x]) 8 replace the use of x with xi 9 for each variable a that S defines 10 count[a] = Count[a] + 1 11 i = Count[a] 12 push i onto Stack[a] 13 replace definition of a with ai
例如,下面的c程式碼:
1 a = x + y; 2 b = a - 1; 3 a = y + b; 4 b = 4 * x; 5 a = a + b;
經過SSA轉換之後會變成這樣:
1 a1 = x0 + y0; 2 b1 = a1 - 1; 3 a2 = y0 + b1; 4 b2 = 4 * x0; 5 a3 = a2 + b2;
7.2.2 Phi函數
前面說了線性程式碼的SSA轉換過程,那非線性程式碼應該怎麼處理呢?
例如下面的控制流圖,SSA轉換之後L5處使用的b是哪一個b?:
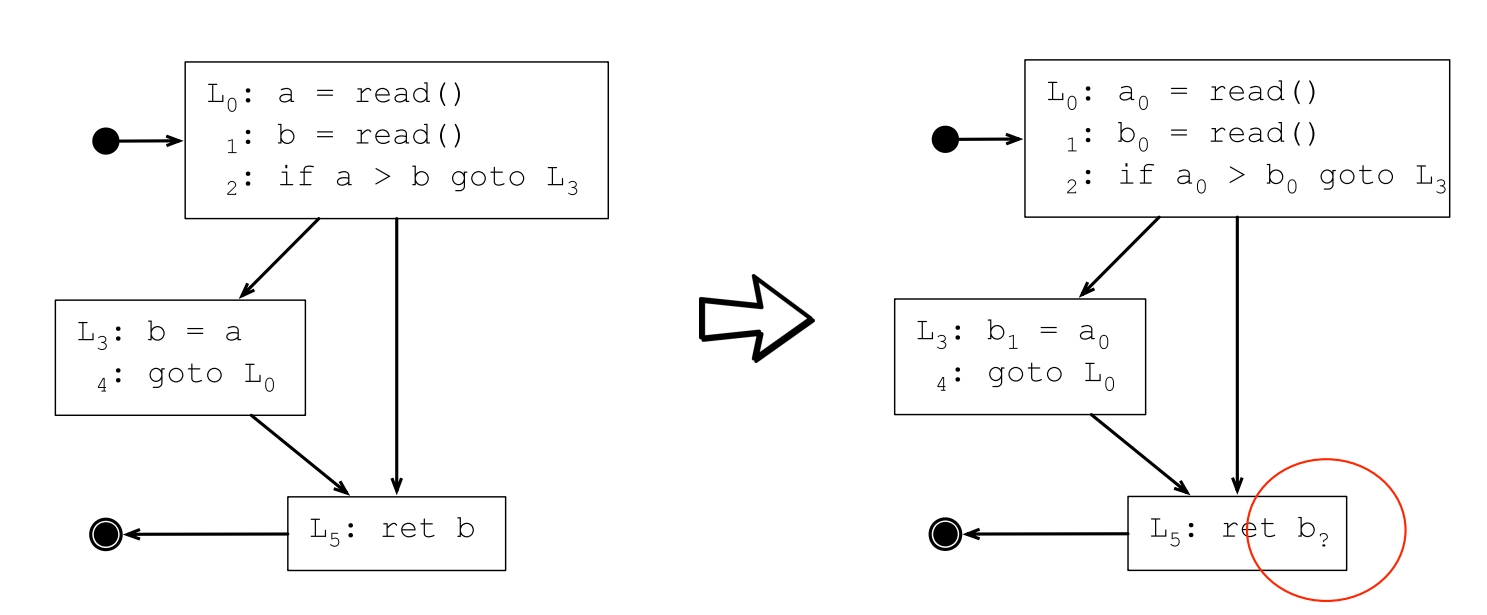
答案是要看情況,如果控制流圖上從L4執行到L5,則L5處的b應該是b1;如果是從L2執行到L5,則L5處的b應該是b0。
為了處理這種情況,需要引入phi函數(φ),φ函數會根據路徑做選擇,根據進入φ函數的路徑選擇不同的定義。
插入φ函數之後的SSA轉換結果如下:
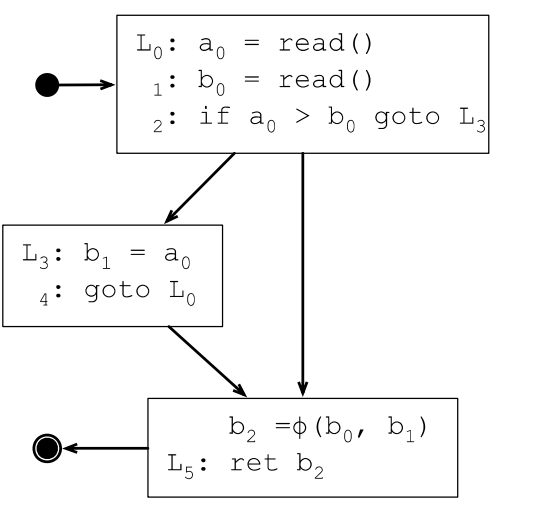
φ函數會插入到每個基本塊的最開始地方,對N個變數生成N個φ函數,φ函數的引數個數取決於執行到該基本塊的直接前驅有幾個。
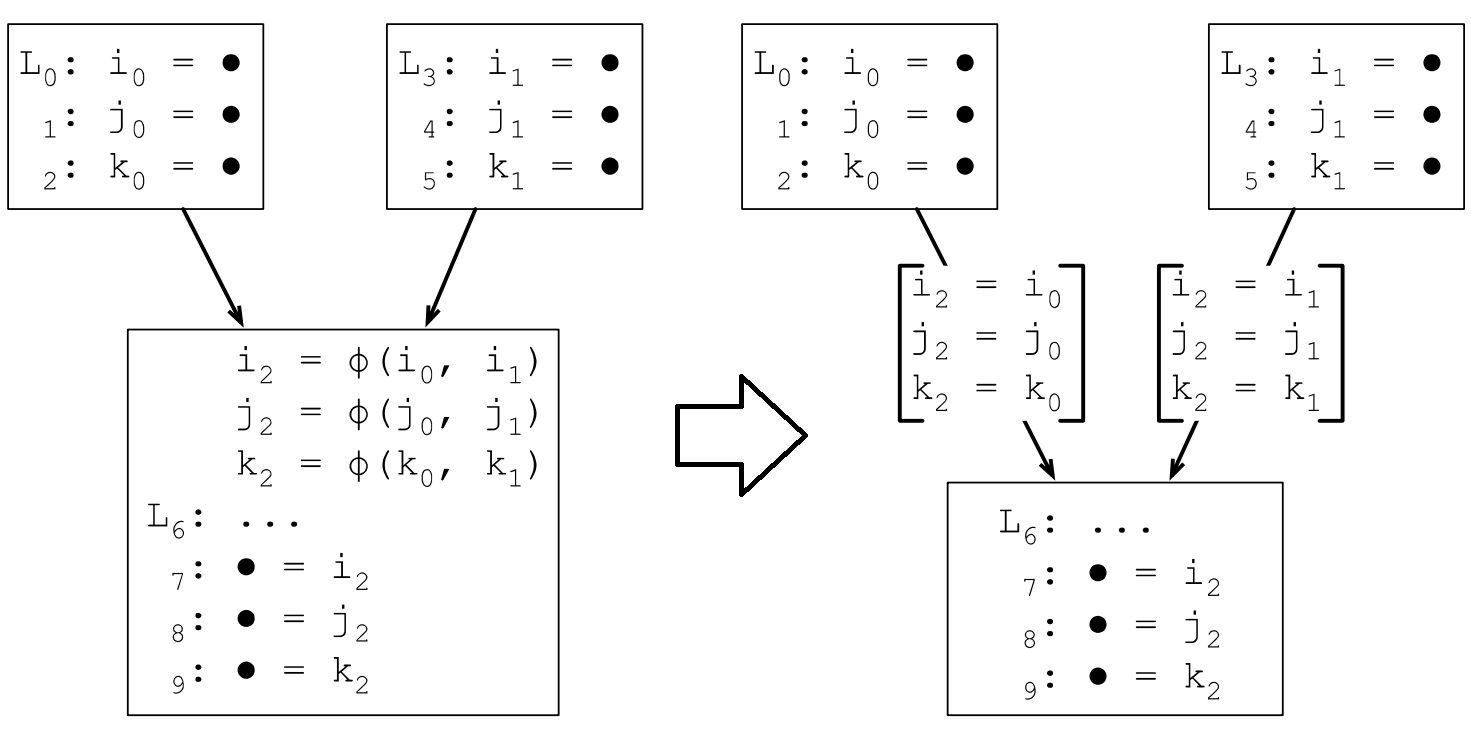
7.2.3 臨界邊
如果一條邊的起始點BB有多個直接後繼BB,終止點的BB有多個前驅BB,則稱為該邊為臨界邊。
7.2.4 臨界邊分裂
在臨界邊上插入一個空的BB(這個BB只有一個簡單的goto語句),來解決臨界邊的上的φ函數自動注入問題。
7.2.5 φ函數的插入策略
- 存在一個基本塊x包含b的定義
- 存在一個非x的基本塊y包含b的定義
- 存在至少一條路徑Pxz從x到z
- 存在至少一條路徑Pyz從y到z
- Pyz和Pxz除了z節點外,沒有其他公共節點
- z不會同時出現在Pxz和Pyz路徑中間,但可以出現在其中一條路徑的中間
7.2.6 SSA正規化的支配屬性
在一個有根的有向圖中,d支配n的意思是所有從根節點到n的路徑都通過d。
在嚴格SSA正規化(嚴格的意思是所有變數都是在使用前初始化)程式中,每個變數的定義都支配它的使用:
在基本塊n中,如果x是φ函數的第i個引數,則x的定義支配n的第3個前驅。
在一個使用x的不存在φ函數的基本塊n中,x的定義支配基本塊n。
7.2.7 支配前沿(The Dominance Frontier)
一個節點x嚴格支配節點w,當且僅當x支配w,並且x≠w。
節點x的支配前沿是所有具有下面屬性的節點w的集合:x支配w的前驅,但不嚴格支配w。
支配前沿策略:如果節點x函數變數a的定義,那麼x的支配前沿中的任意節點z都需要一個a的φ函數。
支配前沿迭代:因為φ函數本身會產生一個定義,所以需要回圈執行支配前沿策略,直到沒有節點需要額外增加φ函數。
定理:迭代支配前沿策略和迭代路徑覆蓋策略生成同樣的φ函數集合。
7.2.8 支配前沿的計算
DF[n] = DFlocal[n] ∪ { DFup[c] | c ∈ children[n] }
Where:
DFlocal[n]: 不被n嚴格支配(SSA的1989年版本要求的是嚴格支配,但1991年版本優化成直接支配,前一篇在ACM會議上,後一篇在ACM期刊上,Cytron果然是混職級的高手
7.3.3 根據控制流圖生成支配樹
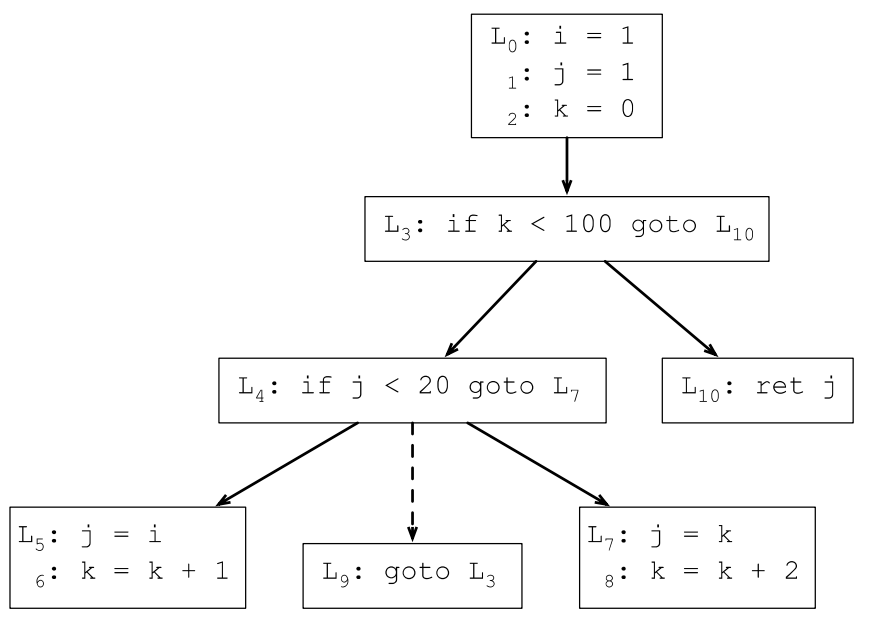
7.3.4 計算支配前沿
一般從支配樹的葉子節點開始計算,第一輪計算所有葉子節點:
DF(7) = {9}, DF(9) = {3}, DF(5) = {9}, DF(10) = {}
第二輪去掉支配樹的所有葉子節點,計算第二輪葉子節點的支配前沿:
DF(4) = {3}
第三輪刪掉葉子節點,並計算當前葉子節點的支配前沿:
DF(3) = {3}
第四輪刪掉葉子節點,並計算當前葉子節點的支配前沿:
DF(0) = {}
7.3.5 插入φ函數
上一節求出來的DF集合其實只有2個元素,所以只需要在L3和L9的基本塊開始處插入φ函數,存在多種定義的變數只有j和k,所以下面在L3和L9插入j和k的φ函數:
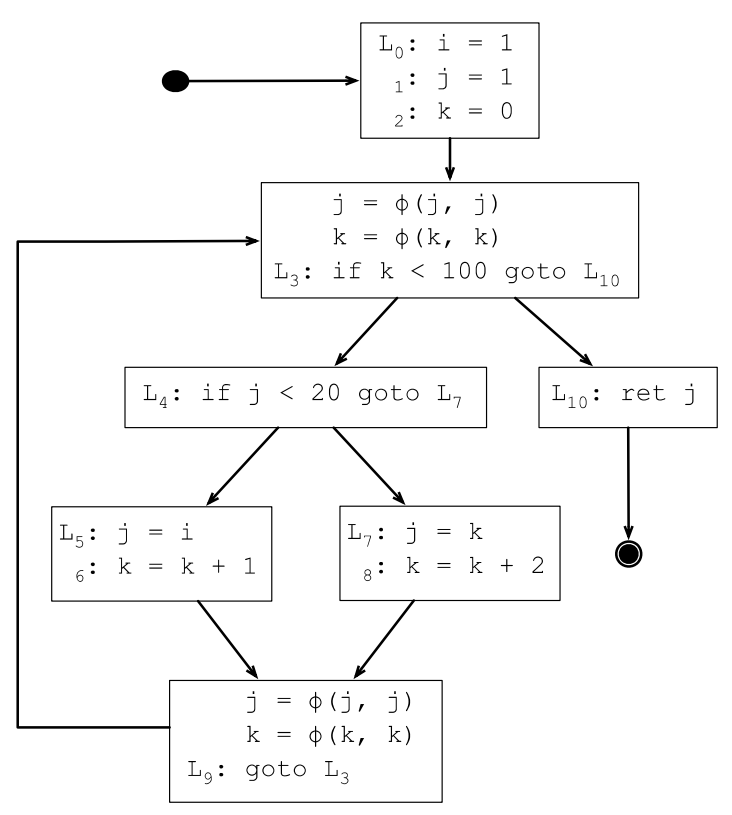
7.3.6 φ函數的引數個數
是否存在只有一個前驅的φ函數?如果只有一個前驅,那說明變數只有一個定義,自然就不需要φ函數。
是否存在引數多餘2個的φ函數?如果前驅個數大於2,自然就會出現引數多餘2的φ函數。
7.3.7 變數重新命名
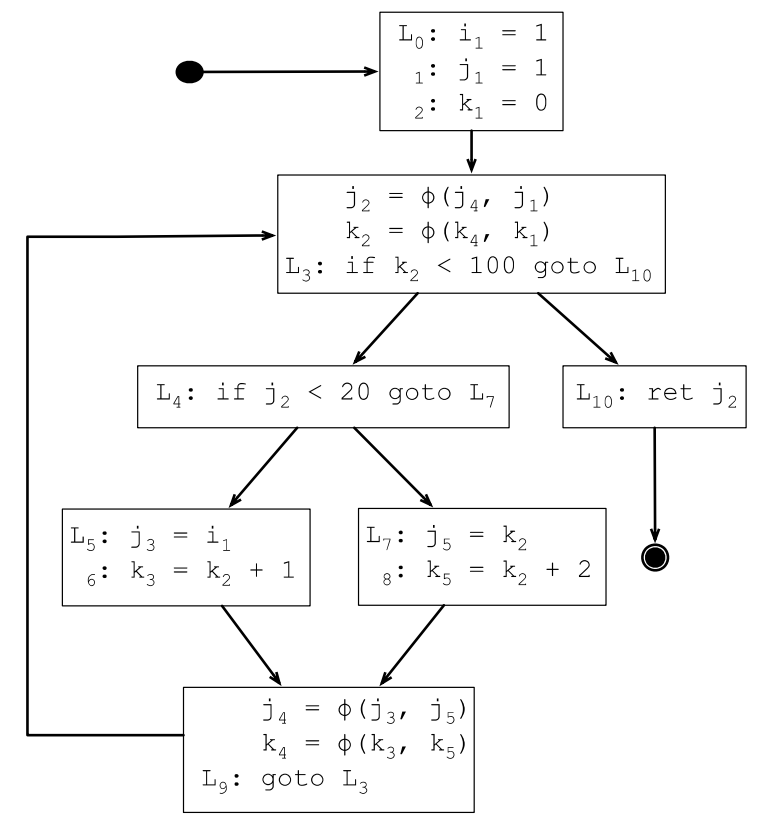
7.3.8 優化SSA正規化
上面生成的SSA正規化,從SSA的定義上看雖然已經是最簡的了,但可能存在一些用不上的變數定義,砍掉這些冗餘的定義是生命週期檢查的工作,經過生命週期檢查,僅在變數i還處在生命週期範圍內的程式點才需要插入i的φ函數。
下面L1處的i的定義後面沒機會使用了,所以L1處的φ函數插入是不必要的:
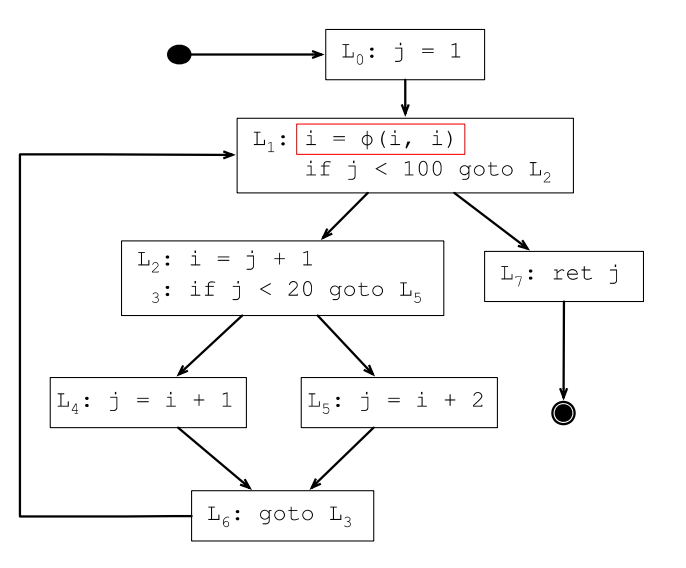
7.4 使用SSA簡化分析
SSA正規化可以用來簡化各種基於資料流的分析。SSA正規化之前,資料流分析的某個變數的定義是一個集合,SSA正規化轉換之後這些變數都變成了唯一定義;而且由於每個變數只有一次定義,相當於說每個變數都可以轉換成常數(迴圈內定義的變數除外,每次迴圈迭代,變數都會被重新定義)。
7.4.1 簡化冗餘程式碼刪除
如果一個變數定義了,沒有使用,並且該定義的語句也沒有其他副作用,可以將該變數定義的語句刪除。(SSA之前變數是否被使用的含義就要複雜多了,因為會有多個版本的變數定義)
給每個SSA轉換之後的每個變數儲存一個計數器,初始化為0。遍歷一遍程式碼,每次使用就將計數器加一,遍歷完如果某個變數的使用計數器為0,則可以刪除變數的定義語句。
7.4.2 簡化常數傳播
因為每個變數的定義都只有一個定義,所以在變數定義時就能判斷變數是常數,還是真的變數。如果變數的定義依賴某個外部輸入,則它不是常數。如果變數的定義依賴的是一個常數,或者依賴的變數是一個常數,則常數可以一直傳播下去,所有類似的變數都能轉換成常數。直到明確所有變數都是依賴某個外部輸入。
如果碰到φ函數怎麼辦?因為φ函數會給變數的賦值增加多種可能性,所以變數的定義變成了一個集合,只有當集合中所有定義都是常數的情況下,才能將該變數轉換成常數。
下面是llvm的常數傳播的實現:

7.4.3 SSA正規化轉換之後的生命週期分析
新的生命週期分析演演算法如下:
1 For each statement S in the program: 2 IN[S] = OUT[S] = {} 3 For each variable v in the program: 4 For each statement S that uses v: 5 live(S, v) 6 live(S, v): 7 IN[S] = IN[S] ∪ {v} 8 For each P in pred(S): 9 OUT[P] = OUT[P] ∪ {v} 10 if P does not define v 11 live(P, v)
7.5 SSA簡史
- 「An Efficient Method of Computing Static Single Assignment Form, 」 appeared in the conference Record of the 16th ACM Symposium on principles of Programming Languages (Jan. 1989). https://c9x.me/compile/bib/ssa.pdf
- Efficiently Computing Static Single Assignment Form and the Control Dependence Graph, ACM Transact~ons on Programmmg Languages and Systems, VO1 13, NO 4, October, le91, Pages 451.490. Efficiently computing static single assignment form and the control dependence graph (utexas.edu)
- Lengauer, T. and Tarjan, R. "A Fast Algorithm for Finding Dominators in a Flowgraph", TOPLAS, 1:1 (1979) pp 121-141
- Briggs, P. and Cooper, K. and Harvey, J. and Simpson, L. "Practical Improvements to the Construction and Destruction of Static Single Assignment Form", SP&E (28:8), (1998) pp 859-881