論文解讀(GraphMAE)《GraphMAE: Self-Supervised Masked Graph Autoencoders》
論文資訊
論文標題:GraphMAE: Self-Supervised Masked Graph Autoencoders
論文作者:Zhenyu Hou, Xiao Liu, Yukuo Cen, Yuxiao Dong, Hongxia Yang, Chunjie Wang, Jie Tang
論文來源:2022, KDD
論文地址:download
論文程式碼:download
1 Introduction
GAE 研究困難之處:
- 首先,過度強調結構資訊。
- 大多數 GAEs 利用重建邊連線作為目標來鼓勵鄰居 [3,17,20,26,31,42] 之間的拓撲緊密性。該型別方法適用與鏈路預測和節點聚類,對節點和圖分類卻不令人滿意。
- 其次,無失真壞的特徵重構可能不夠健壯。
- GAEs[3,20,26,27,31],大多使用有風險學習瑣碎解決方案的普通體系結構。
- 第三,均方誤差(MSE)可能是敏感的和不穩定的。
- 現有的具有特徵重建 [17,18,27,31,42] 的 GAEs 都採用了 MSE 作為標準,沒有額外的預防措施。然而,已知 MSE 存在不同的特徵向量範數和維數[5] 的詛咒,因此可能導致自動編碼器訓練的崩潰。
- 第四,解碼器的架構很少有表現力。
- 大多數 [3、16-18、20、26、42] 利用MLP作為解碼器。由於圖中大多數節點所含的資訊較少,使用普通的 MLP 解碼器可能無法彌補編碼器的表示和解碼器目標之間的差距。
- 大多數 [3、16-18、20、26、42] 利用MLP作為解碼器。由於圖中大多數節點所含的資訊較少,使用普通的 MLP 解碼器可能無法彌補編碼器的表示和解碼器目標之間的差距。
2 Method
整體框架:
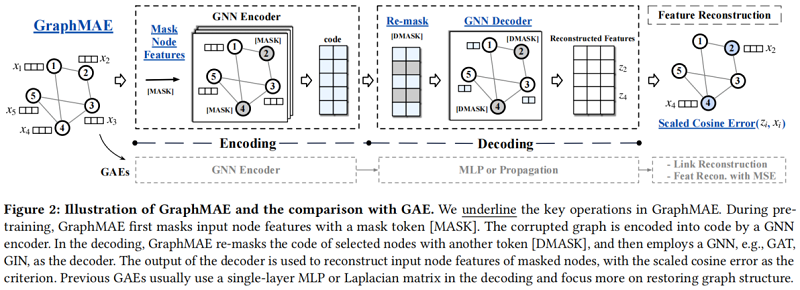
核心思想:重構掩蔽節點特徵。
引入:
-
- Q1: What to reconstruct in GAEs?
- Q2: How to train robust GAEs to avoid trivial solutions?
- Q3: How to arrange the decoder for GAEs?
- Q4: What error function to use for reconstruction?
2.1 Details
Q1: Feature reconstruction as the objective
重建特徵資訊,不考慮結構資訊,Graph-less Neural Networks [58] 也證明了 MLP 在節點分類中的強大。
Q2: Masked feature reconstruction
自編碼器容易陷入 「identity function」 (恆等對映)的問題[41]。對於影象等高維資料,這不是一個嚴重的問題,但是對於圖資料來說,其維度相對較小,所以效果並不是很好[3, 20, 26, 27, 31]。
本文采用掩碼自動編碼器作為 GraphMAE 的主幹。
形式上,取樣節點子集 $\tilde{\mathcal{V}} \subset \mathcal{V}$,並使用一個掩碼標記(mask token)[MASK] 來掩蓋該節點子集每個節點的特徵,即一個可學習的向量 $x_{[M]} \in \mathbb{R}^{d}$。因此,掩蔽特徵矩陣 $\widetilde{X}$ 可以定義為:
$\tilde{x}_{i}=\left\{\begin{array}{ll}x_{[M]} & v_{i} \in \widetilde{\mathcal{V}} \\x_{i} & v_{i} \notin \widetilde{\mathcal{V}}\end{array}\right.$
GraphMAE的目標是通過給定部分觀測到的節點特徵矩陣 $\widetilde{X}$ 和輸入鄰接矩陣 $A$,重構 $\widetilde{V}$ 中節點特徵矩陣。
本文采用統一的隨機抽樣策略來掩蔽節點,均勻分佈的隨機抽樣使得一個節點的鄰居既不是都是掩蓋的,也不是全部可見的,這有助於防止潛在的偏置中心。本文考慮了一個較大的掩蔽率,以減少屬性圖中的冗餘。
另一方面,[MASK] 的使用可能會造成訓練和推理之間的不匹配,因為 [MASK] 標記在推理[49]過程中不會出現。本文實驗發現,「leave-unchanged」的策略實際上損害了GraphMAE的學習,而 「random-substitution」 的方法可以幫助形成更多高質量的表徵。
Q3: GNN decoder with re-mask decoding
由於 MLP 的「identity function」 問題,所以本文使用單層GNN作為其解碼器。GNN解碼器可以基於一組節點而不僅僅是節點本身來恢復一個節點的輸入特徵,從而幫助編碼器學習高階潛在程式碼。
為提高解碼器解碼潛在表示,本文提出一種 re-mask decoding 技術來處理潛在表示 $H$。即,對 Encoder 中的掩蔽節點再次進行 mask token [DMASK] 處理,也就是$\boldsymbol{h}_{[M]} \in \mathbb{R}^{d_{h}}$。具體來說,重新掩碼的 潛在表示 $\widetilde{H}=\operatorname{REMASK}(H)$ 為:
$\tilde{\boldsymbol{h}}_{i}=\left\{\begin{array}{ll}\boldsymbol{h}_{[M]} & v_{i} \in \widetilde{V} \\\boldsymbol{h}_{i} & v_{i} \notin \widetilde{\mathcal{V}}\end{array}\right.$
實證檢驗表明,GAT 和 GIN 編碼器分別是節點分類和圖分類的良好選擇。解碼器只在自監督訓練階段使用,因此可以選擇任意型別的GNN解碼器。
Q4: Scaled cosine error as the criterion
對於特徵重建的 MSE 損失,由於在最小化接近 $0$ 的時候很難優化,所以GraphMAE採用了餘弦誤差來度量重建效果。同時,引入可放縮的餘弦誤差(Scaled Cosine Error)來進一步改進餘弦誤差。
本文設定 $\gamma>1$ ,好處是當置信度高的時候,誤差將快速收斂到 $0$,從而調整了不同樣本的權重。給定原始特徵矩陣 $X$ 和解碼器輸出 $Z=f_{D}(A, \widetilde{H})$,放縮的餘弦誤差的定義為:
$L=\frac{1}{|\widetilde{\mathcal{V}}|}\left(1-\frac{x_{i}^{T} z_{i}}{\left\|x_{i}\right\| \cdot\left\|z_{i}\right\|}\right)^{\gamma}, \gamma \geq 1$
放縮因子 $\gamma$ 是一個在不同資料集上可調整的超引數,可以被看作是一種自適應的樣本權重調整,每個樣本的權重隨著重建誤差的不同進行調整。某種程度上類似於Focal Loss [22]。
Figure 1 是架構設計對比:

2.2 Training and Inference
首先,給定一個輸入圖,我們隨機選擇一定比例的節點,並用掩模標記[MASK]替換它們的節點特徵。我們將具有部分觀察到的特徵的圖輸入編碼器,以生成編碼的節點表示。在解碼過程中,我們重新掩碼所選的節點,並用另一個標記[DMASK]替換它們的特性。然後將解碼器應用於重新掩碼圖,利用所提出的尺度餘弦誤差重建原始節點特徵。
對於下游應用程式,編碼器應用於輸入圖,在推理階段沒有任何掩蔽。生成的節點嵌入可用於各種圖學習任務,如節點分類和圖分類。對於圖形級的任務,我們使用一個非引數化的圖池化(READOUT)函數,例如,MaxPooling,MeanPooling,以獲得圖形級的表示 $\boldsymbol{h}^{g}=\operatorname{READOUT}\left(\left\{\boldsymbol{h}_{i}, v_{i} \in \mathcal{G}_{g}\right\}\right)$。此外,與[16]類似,GraphMAE還能夠將預先訓練過的GNN模型魯棒地轉移到各種下游任務中。在實驗中,我們證明了GraphMAE在節點級和圖級應用中都具有競爭力的效能。
3 Experiments
3.1 Node classificatio
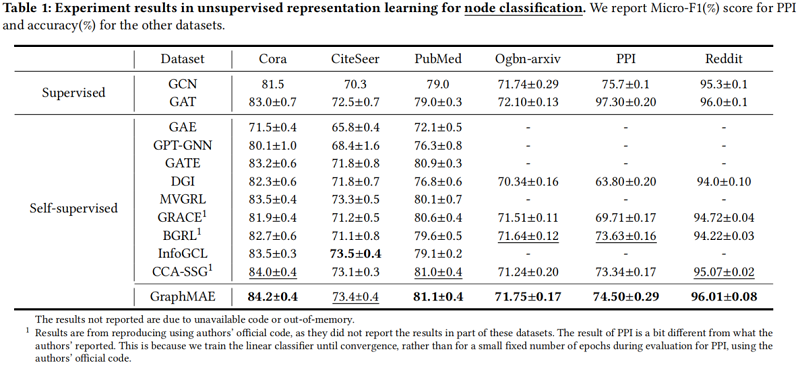
3.2 Graph classification
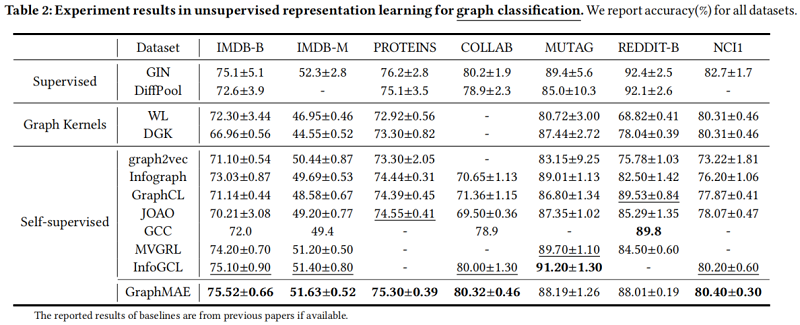
3.3 Transfer learning on molecular property prediction

3.4 Ablation Studies
Effect of reconstruction criterion & Effect of mask and re-mask

Effect of mask ratio
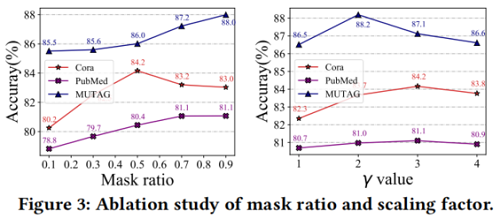
Effect of decoder type

4 Conclusion
貢獻:
-
- MAE 思想用於圖上;
- 提出一種放縮餘弦誤差;
修改歷史
2022-06-17 建立文章
因上求緣,果上努力~~~~ 作者:Learner-,轉載請註明原文連結:https://www.cnblogs.com/BlairGrowing/p/16384404.html