[自制作業系統] 第07回 認識保護模式之地址對映
目錄
一、前景回顧
二、實體地址、線性地址和虛擬地址
三、記憶體為什麼要分頁
四、一級頁表
五、二級頁表
前面我們說到,保護模式下有著三大特點:地址對映、特權級和分時機制。從我的學習角度來說,我認為地址對映這一塊的知識點尤為繁雜,所以會花費相對比較多的時間來講述,話不多說,開整。
在認識地址對映之前,我們來搞懂這三個地址的含義。
實體地址就是實體記憶體中真正的地址,相當於記憶體中每一個儲存單元的門牌號,具有唯一性。不管在什麼模式下,CPU最終都是以實體地址去存取記憶體的,一定要充分認識到這一點。
在真真實模式下,「段基址+段內偏移地址」經過段部件的處理,直接輸出的地址就是實體地址,CPU可以直接使用此地址存取記憶體。
而在保護模式下,「段基址+段內偏移地址」經過段部件的處理,輸出的地址被稱為線性地址,其實此處段基址已經不再是真正的地址了,而是段選擇子,它本質上是一個索引,通過這個索引便能在GDT中找到相應的段描述符,而段基址就在段描述符中,這個內容在上一回已經提到過。得到了線性地址後,此時我們需要判斷一下系統是否開啟了分頁機制(分頁機制在下面就會提到),如果開啟了分頁機制,那麼此時的線性地址又稱為虛擬地址,虛擬地址需要通過頁表對映得到真實的實體地址,這樣CPU才能存取到記憶體。如果沒有開啟分頁機制,此時線性地址就被認為是實體地址,將被CPU直接用來存取記憶體。
總結一下就是下面這張圖:

濃縮一下,其實上面講的東西就是我們常聽說的MMU,它的作用其實就是地址轉換。

MMU是記憶體管理單元,我們的每一個線性地址,通過MMU轉換後,便能得到其實際對應的實體地址,MMU是硬體上提供的地址轉換電路,我們不必操心。我們實際要關心的是,MMU是如何轉換的呢?換句話說,應該是有一個類似表格的結構,表中每一個虛擬地址都一一對應了一個實體地址,我們提供給MMU一個虛擬地址,MMU通過該表查詢,便能得到該虛擬地址對應的真實地址。實際上的確是有這麼一個表格,它的名稱叫做頁表,頁表的構建是基於分頁機制的,而不是隨隨便便劃分的頁表。
一直以來我們都是在記憶體分段機制下執行的,目前未出問題看似良好,可是想象一下,當我們的實體記憶體不足時會怎麼辦?如下圖所示:

當系統中有三個程序A、B、C在執行,實體記憶體還剩餘15MB。此時如果程序B結束了,但是新來了一個程序D需要佔用20MB+3KB的實體記憶體,此時由於執行環境未開啟分頁功能,「段基址+段內偏移」產生的線性地址就是實體地址,程式中的實體地址是連續的,就導致沒有足夠的記憶體空間供程序D使用。此時就需要將程序A的段A3或者程序C的段C1換出,具體換出哪一部分是需要參考換入換出演演算法,這裡不深入講解,總之只需要知道,我們需要換出一個段來騰出空間給程序D。
問題解決了,但是又沒完全解決,這個方法中,如果程序的段特別大,那麼換出時要將整個段全部搬運到外存,也就是硬碟上,這種IO操作太多了導致系統響應奇慢無比,令人無法接受。這個問題的本質是因為在我們的程序中,程式碼和資料是以段為基本單位進行儲存,而每個程序的段的大小是不一致的。既然段的大小不固定,於是接下來我們做了一點改變:我們規定:頁是段的更小的劃分,且頁的大小是固定的。目前普遍的作業系統中規定頁的大小是4KB,這樣一個段就可以被劃分成多個頁,下次再換入換出時,我們就只需要換出部分頁即可,而不用將整個段換出,這樣便能避免IO操作太多導致系統響應慢的問題。
可是仔細一想,這個解決方法還是有未能盡善盡美的地方,假如程序A段的A3和程序C的段C1現在都在執行,不允許換出部分頁,這該如何是好?
究其本質是因為在我們沒有開啟分頁機制時,程式中使用的線性地址就是真實的實體地址,這兩個地址都是連續的。我們知道線性地址是編譯器編譯得出的,它必須是連續的,所以連帶著實體地址也是連續的。如果有這麼一個方法,讓線性地址依舊連續(因為這是編譯器決定的)但是讓實體地址不連續,這樣不就可以將記憶體空間中的不連續實體地址被利用起來了麼?
於是分頁機制就呼之欲出了,分頁機制結合前面說的分頁方法,將實體記憶體和線性記憶體劃分為同等大小的頁,一頁線性記憶體可以對應一頁真實的實體記憶體,這樣就可以讓連續的線性地址對應上不連續的實體地址。
說這麼多,我們從宏觀角度來看看分頁機制的實現吧。

我們的CPU進入保護模式後有了4GB的定址空間,這就是定址空間就是指的線性地址空間,它在邏輯上是連續的。分頁機制將所有段都劃分為同等大小的頁,與此同時,假設我們的實體記憶體也是4GB,我們將實體記憶體頁劃分為若干個頁,虛擬地址空間的每一頁通過一個對映關係就可以一一對應到實體地址空間中每一頁。這個對映關係就是接下來我們要講的頁表。
前面說過分頁機制可以讓連續的線性地址通過某種對映關係對應上不連續的實體地址,頁表就是這個對映關係。
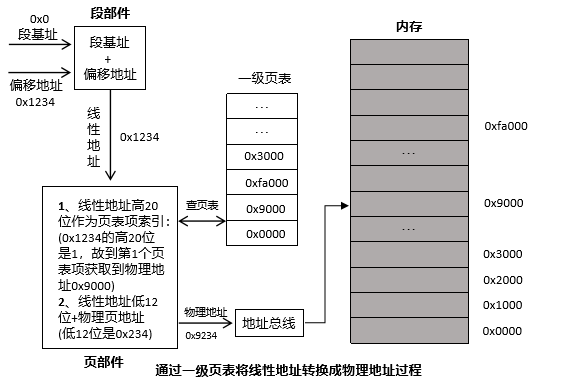
通常來說,一頁的大小是4KB,現在我們來計算一下4GB的空間可以劃分為多少個頁,即4GB/4KB=1M個頁。也就是說4GB的空間可以容納1048576個頁,頁表中自然也要有1048576個頁表項。也就是我們要說的一級頁表,如圖所示。

由於頁的大小是4KB,所以頁表項中的實體地址都是4K的整數倍,用十六進位制來表示的地址,其低3位都是0。頁表介紹完了,具體如何使用呢?也就是如何將線性地址轉換成實體地址呢?還是舉一個小小的例子來說明:
在保護模式下的線性地址有32位元,低12位元被視為頁內偏移地址,因為我們知道任何一個線性地址肯定是要落在一個物理頁中。所以低12位元是用於在物理頁中偏移地址的。高20位用來表示頁的數量,也就是用來在頁表中索引物理頁的。假設現在有一個線性地址為0x00001234,其地址轉換過程如下圖所示:
一級頁表就到此為止,接下來我們看看二級頁表。
前面講述了一級頁表,並以一級頁表作為原型講述了地址轉換過程,既然有了一級頁表為什麼還要來弄一個二級頁表呢?原因如下:
1、一級頁表中最多容納1M個頁表項,每個頁表項是4個位元組,如果頁表項全滿的話,那就是4MB大小。
2、一級頁表中的所有頁表項必須提前建好,原因是作業系統要佔用4GB虛擬地址空間的高1GB,使用者程序佔用低3GB。
3、每個程序都有自己的頁表,程序一多,光是頁表佔用的空間就很可觀了。
歸根結底,我們要解決的問題是:能否不要一次性地將全部頁表項建好,而是在需要時動態建立頁表項。
如何解決呢?二級頁表便能很好地解決這個問題。
先來看看二級頁表的模樣,如圖所示:
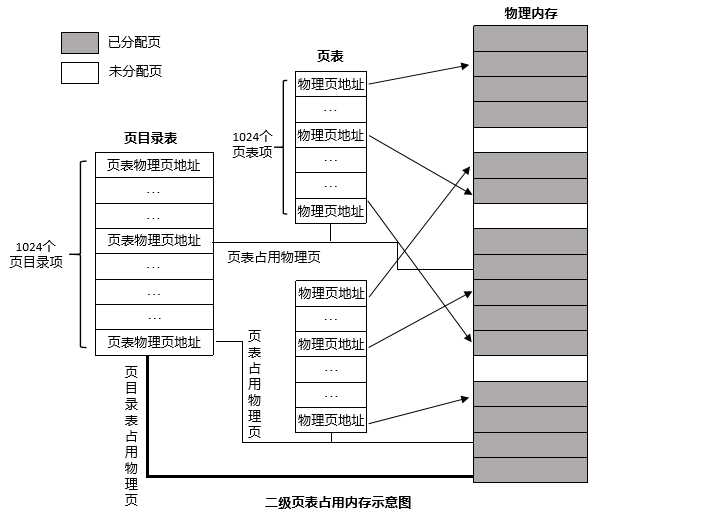
我們有一個頁目錄表,表中共有1024個頁表項,每個頁表項中記錄了一個頁表物理頁地址,每一個頁表中又記錄了1024個物理頁的地址,這裡的每一個物理頁和一級頁表一樣,依舊是一頁4KB大小。故一個頁表項能記錄的記憶體容量為1024x4KB=4MB,一個頁目錄表能記錄的記憶體容量為1024x4MB=4GB,這就達到了32位元地址空間的最大容量。所以理論上每一個線性地址都能落在一個物理頁中。
我們還是來看看,在二級頁表下,給定一個線性地址如何通過二級頁表來轉換成實體地址:
1、用虛擬地址的高10位乘以4,作為頁目錄表的索引號,再加上頁目錄表的實體地址,所得到的就是頁目錄項的實體地址,讀取該頁目錄項,從中獲取到頁表的實體地址。
2、用虛擬地址的中間10位乘以4,作為頁表的索引號,再加上在第一步中得到的頁表實體地址,便是頁表項的實體地址,讀取該頁表項,從中獲取到物理頁的地址。
3、虛擬地址的低12位元是物理頁內的偏移量,用低12位元加上第二步得到的物理頁地址的和,便是最終轉換的實體地址。
以虛擬地址0x01234567為例,其轉換為實體地址的流程圖如下所示:

這裡說明一下,頁目錄表的實體地址是存放在CR3暫存器中的,後面我們設計的二級頁表的頁目錄表實體地址也將會存放在CR3暫存器中,方便CPU呼叫。
熟悉了二級頁表的工作原理,我們回過頭來看看,為什麼說二級頁表能解決前面一級頁表的那三個問題。這三個問題的重點就是想要說明一級頁表佔用的記憶體空間會過大,那麼二級頁表佔用的記憶體空間為多少呢?我們試著來分析一下,首先,對於每個程序來說,頁目錄表是必不可少的,頁目錄表佔用的記憶體只有4KB。而頁表是可以不事先建好的,當程序有換入的請求時,假設此時程序請求從硬碟中換入4MB的資料,如果此時記憶體中具有空閒的4MB的記憶體,那麼CPU就將該4MB的記憶體分配給該程序,我們知道,4MB剛好是1M個物理頁的大小。CPU會在記憶體中劃定一頁空閒的物理頁來作為這4MB記憶體的頁表,隨後將該頁表的地址填入到頁目錄表中即可。當這4MB的資料不再需要時,CPU又可以將其換出,然後刪除相應的頁表和頁目錄表中的頁表項資訊。這樣就實現了動態增減頁表,避免頁表佔用過多記憶體的問題。
最後我們來看看頁目錄項和頁表項的內容。
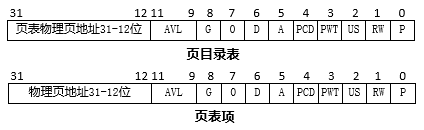
因為頁目錄項和頁表項都是記錄的物理頁的地址,物理頁的大小是4KB,所以地址都是4K的倍數,也就是地址的低12位元都是0,所以只需要記住實體地址的高20位即可,這也就是為什麼我們看圖中頁目錄項和頁表項記錄的地址只有20位的原因,空出來的12位元可以用來新增其他屬性。
本回到此結束,下面我們將開始著手實現一個二級頁表,使系統進入分頁機制下執行。欲知後事如何,請看下回分解。