技術文章 » 軟體專案管理 7.4.2.進度計劃編排-關鍵路徑法

軟體專案管理 7.4.2.進度計劃編排-關鍵路徑法

2022-06-15 15:01:10

【公眾號@ 「專案管理研究所」 將會第一時間更新文章並分享《行業分析報告》】
歸檔於軟體專案管理初級學習路線
第七章 軟體專案進度計劃
《初級學習路線合集 》

前言

大家好，這節我們學習軟體專案管理---進度計劃編排--關鍵路徑法。

基本概念

  1. 最早開始時間（Early start）
  2. 最晚開始時間（Late start）
  3. 最早完成時間（Early finish）
  4. 最晚完成時間（Late finish）


例如：我們看這個任務是10天，最早開始時間ES=1，最早完成時間EF=11，最晚開始時間LS=5，那麼對應最晚完成時間LF=15。

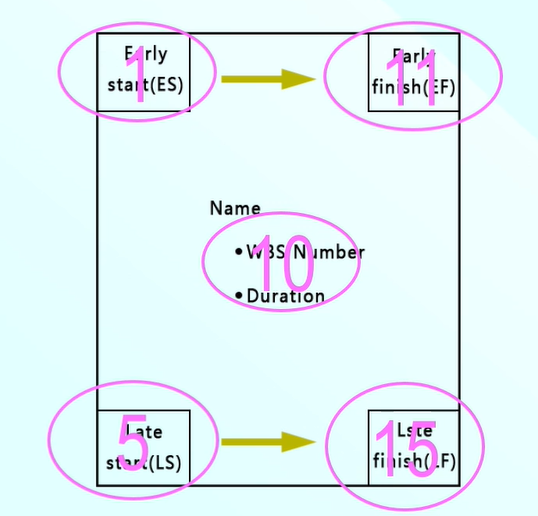
浮動時間

浮動時間是一個任務的機動性，它是一個任務在不影響其它任務或者專案完成的情況下可以延遲的時間量。

例如：下圖這個剛才的任務，可以1號開始，也可以5號開始，有4天的浮動，這就是浮動，這個浮動基本就是個總浮動的概念，我們一般說的浮動也是總浮動。

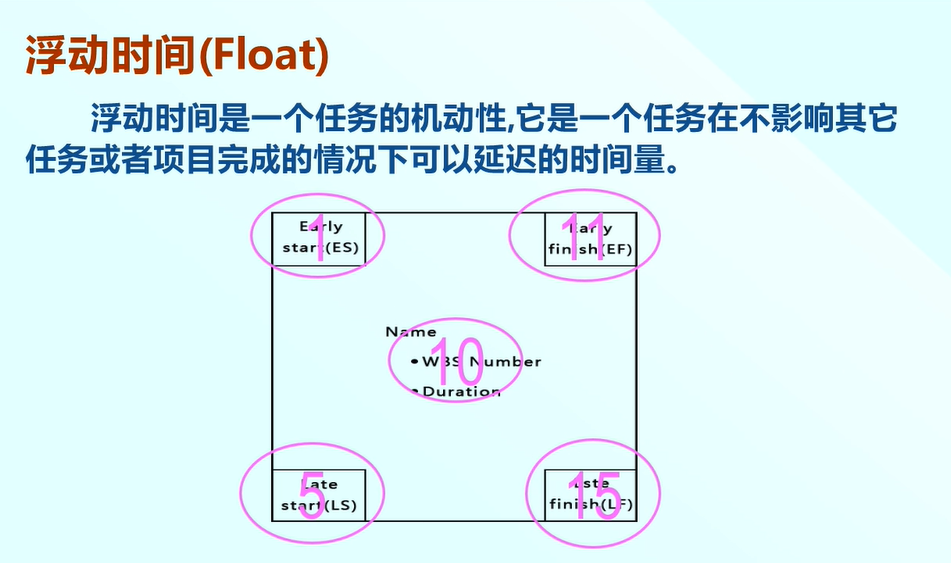
總浮動與自由浮動

如下圖示的任務有4天的總浮動，但是不一定可以自由的使用。

總浮動是在不影響專案最早完成時間的前提下，一個任務可以延遲的時間。

自由浮動是在不影響後置任務最早開始時間的前提下，一個任務可以延遲的時間量。他說明了總浮動的自由性，所以小於等於總浮動。

例如：他的後置任務最早開始時間是13，所以自由浮動時間為2.

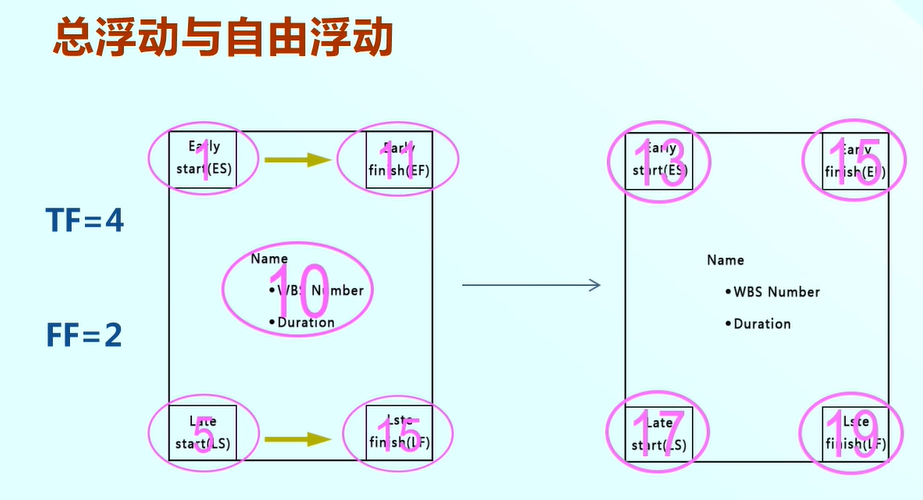
關鍵路徑

  1. 網路圖中最長的路徑
  2. 關鍵路徑是決定專案完成的最短時間。
  3. 時間浮動為0（Float=0）的路徑
  4. 關鍵路徑上任何活動延遲，都會導致整個專案完成時間的延遲
  5. 關鍵路徑可能不止一條

我們看一個專案網路圖：關鍵路徑是A，專案完成的時間是100天。

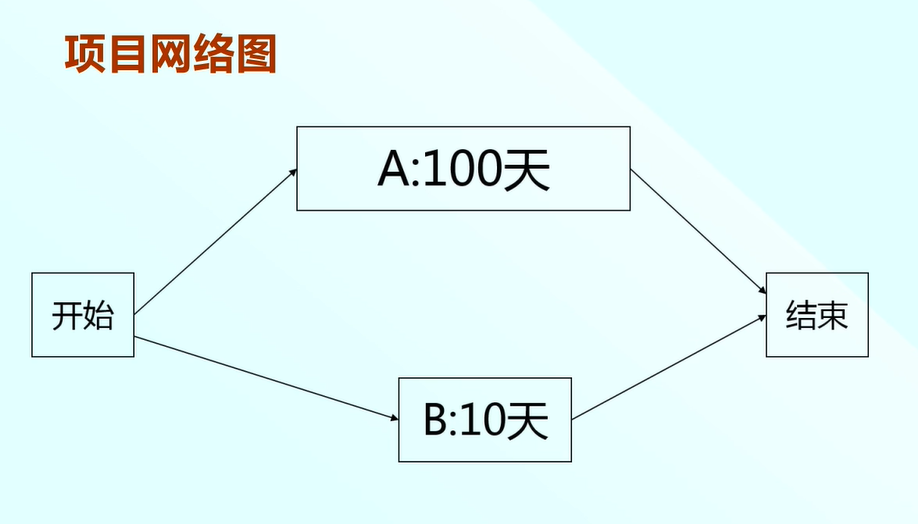
我們將這個網路圖改為甘特圖的形式，專案在100天內完成，A任務沒有浮動，是關鍵路徑。但是B任務相對來說靈活點，是有浮動的，最晚可以第90天開始。

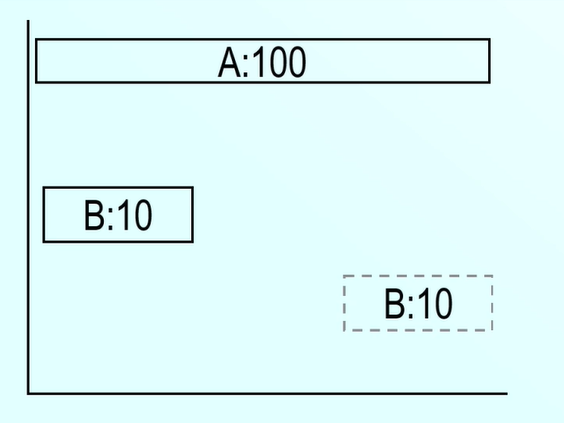
我們先看第一個任務A，從第0天開始，說明任務A的最早開始時間是第0天，那麼他的最早結束時間是100。

所以ES=0可以推匯出EF=100，從左向右，順時針推導。A的最晚完成時間是第100天，歷時是100，所以LF=100，LS=0，從右向左，逆時針推導。

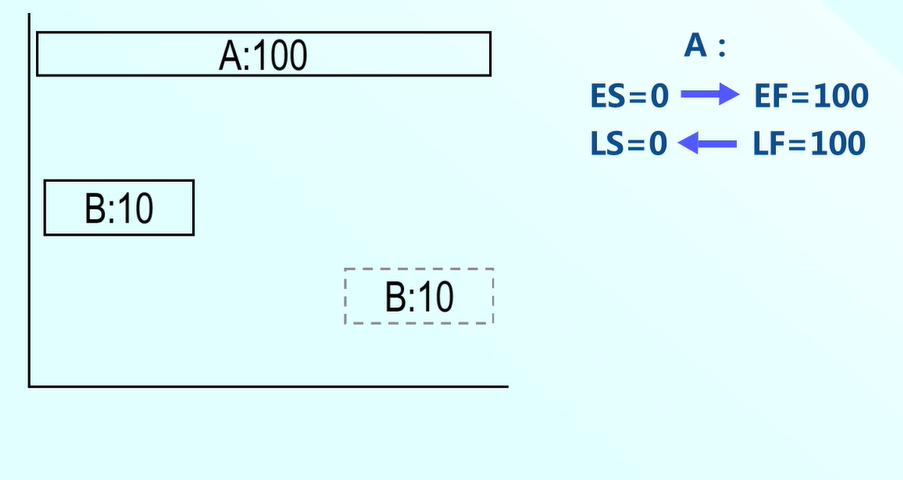
我們再來看任務B的最早開始時間和任務A一樣，都是第0天開始，ES=0，歷時為10，從左向右，推出B的最早完成時間為第10天，則EF=10。

B的最晚完成時間LF=100，從右向左，逆時針推導，B的最晚開始時間為LF-10=90，則LS=90.

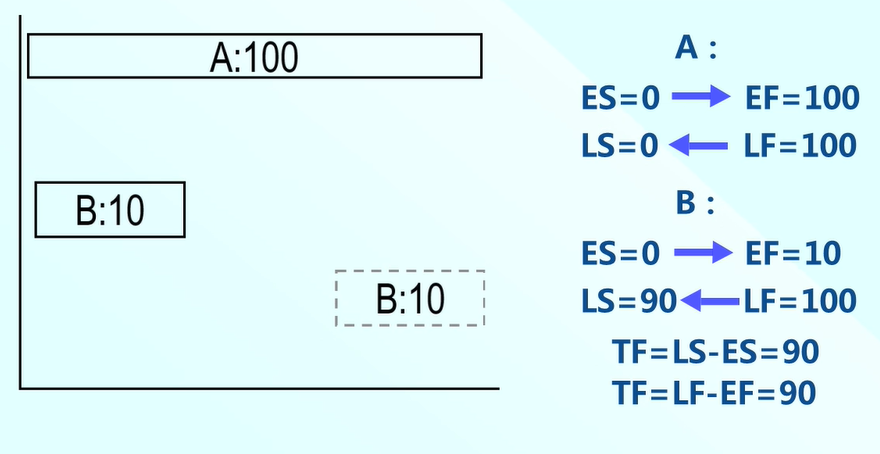
接下來說浮動，剛才說了B有浮動，很明顯看出來有90天浮動，那麼這個浮動是總浮動，TF=LS-ES=90，或者TF=LF-EF=90。

因此我們得出如下圖公式：

翻譯其中一條：EF（最晚結束時間）=ES（最早開始時間）+duration（歷時）

剛才那個專案的任務A和任務B都沒有任務後置的，所以就不牽扯到自由浮動的問題。

現在在任務B的後面加一個任務C，任務C的歷時是5，並且B和C之間加一個延遲Lag，這個Lag=5，既B任務完成5天后，C這個任務才能開始。

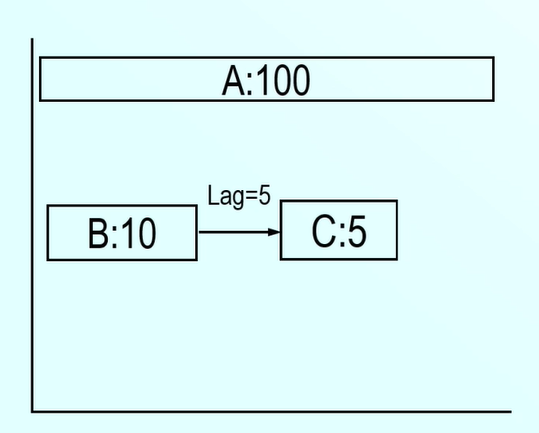
看這個專案關鍵路徑還是A，B和C路徑是有浮動的，但是B任務有了後置任務C之後就不自由了。

那麼任務A這個路徑沒有變化，ES和LS還是和剛才一樣，如圖所示：

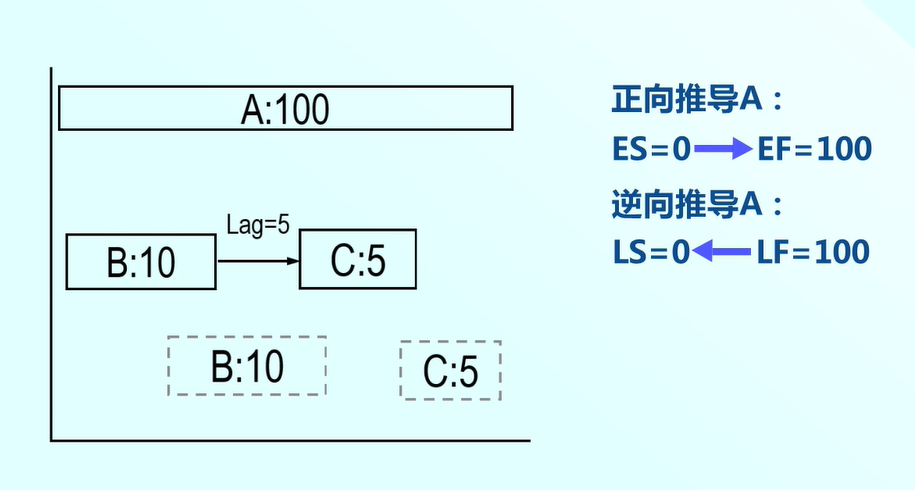
那麼任務C和任務B這條路徑，正向推導最早開始時間和最早結束時間，從左到右。對於任務B而言ES=0，推匯出EF=10.

任務C則ES(c)=EF(B)+lag=15，則EF=ES+歷時5天=20。

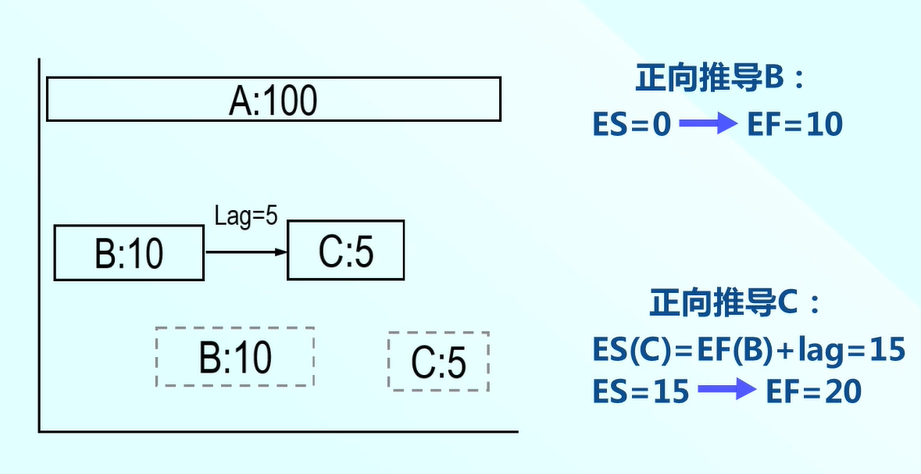
逆向推導最晚結束時間和最晚開始時間，從右向左。首先推導任務C，LF=100，LS=95。

B的LF=LS(c)-Lag(5)=90.則B的LS（最早開始時間）=LF（90）減去歷時10天為80。

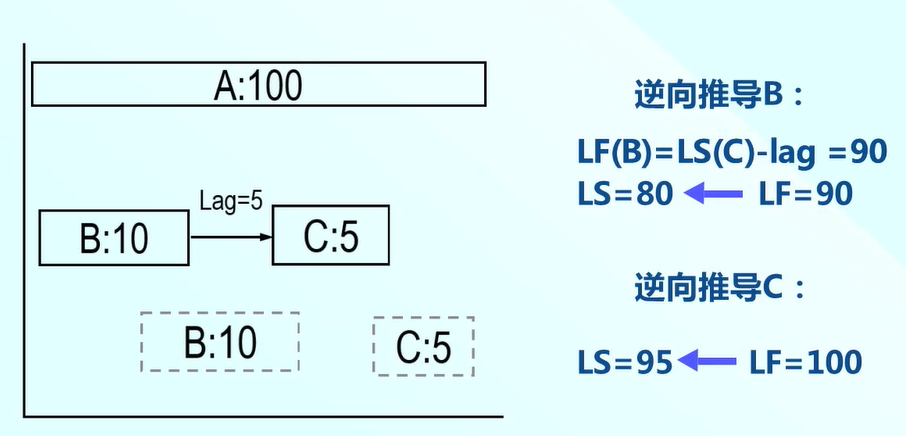
因此我們總結公式如下：
其中S代表後置任務，P代表前置任務。比如ES(S)代表後置任務的最早開始時間。

B的總浮動為80天，但是不一定很自由，為了不影響後置任務C的最早開始時間，則B的自由浮動時間FF為0。

由此我們總結出，正推法確定最早開始時間和最早完成時間。逆推法確定最晚結束時間和最晚開始時間。

正推法

按照時間順序計算最早開始時間和最早完成時間的方法,稱為正推法。

正推法步驟如下：

  1. 確定專案的開始時間,網路圖中第一個任務的最早開始時間是專案的開始時間；
  2. ES+Duration=EF
  3. EF+Lag=ES（s）,當一個任務有多個前置任務時，選擇前置任務中最大的EF加上Lag作為其ES。
  4. 依次類推，從左到右，從上到下，計算每個路徑的所有任務的ES和最早完成時間EF

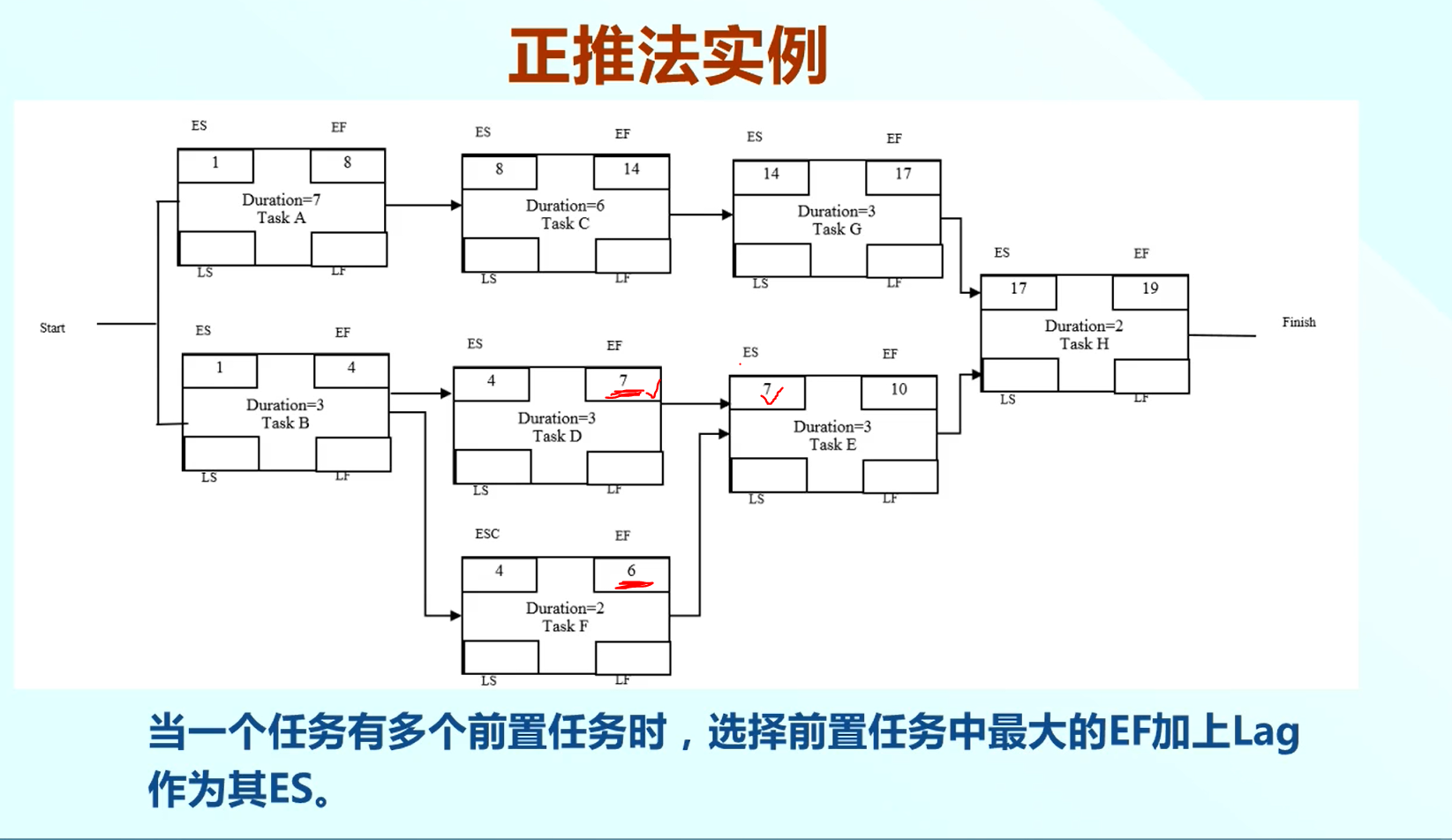
我們看個例子：這是專案的網路圖，而且確定了每個活動的歷時，現在用正推方法來確定每個任務的ES和EF。


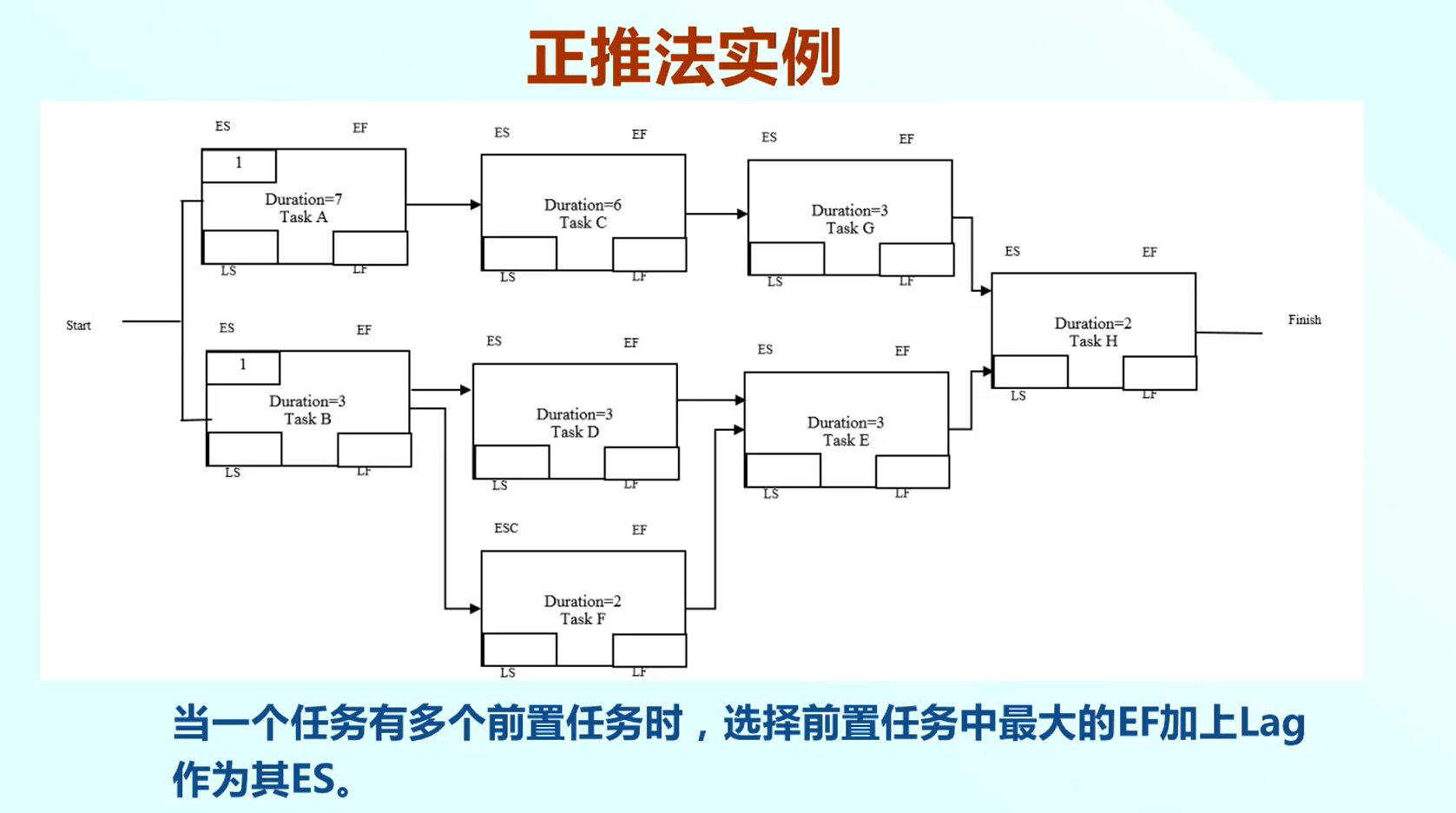
我們先確定專案的開始時間，那麼任務A的開始時間是1，歷時為7，則EF（最早結束時間）=8。

A和C任務之間沒有Lag，所以C的ES為8，因為歷時為6，所以EF為14。以此類推...從左到右，從上到下。

圖中任務E有兩個前置任務，則需要選擇前置任務中最大的EF加上Lag作為其ES，所以選擇任務D的EF=7,因為沒有Lag，所以任務E的ES=7.

逆推法

按照逆時間順序計算最晚開始時間和最晚結束時間的方法,稱為逆推法。

逆推法步驟如下：

  1. 首先確定專案的結束時間,網路圖中最後一個任務最晚完成時間是專案的結束時間；
  2. LF-Duration=LS
  3. LS-Lag=LF（p），當一個任務有多個後置任務時，選擇其後置任務中最小LS減Lag作為其LF
  4. 依次類推，從右到左，從上到下，計算每個任務的最晚開始時間LS和最晚結束時間LF

我們繼續通過逆推法來推導這個專案各個任務的最晚結束時間和最晚開始時間。

首先確定專案完成時間，為了保證專案在最短時間內完成，最後任務H的完成時間是19，因為最後的任務在關鍵路徑上，所以是沒有浮動的。

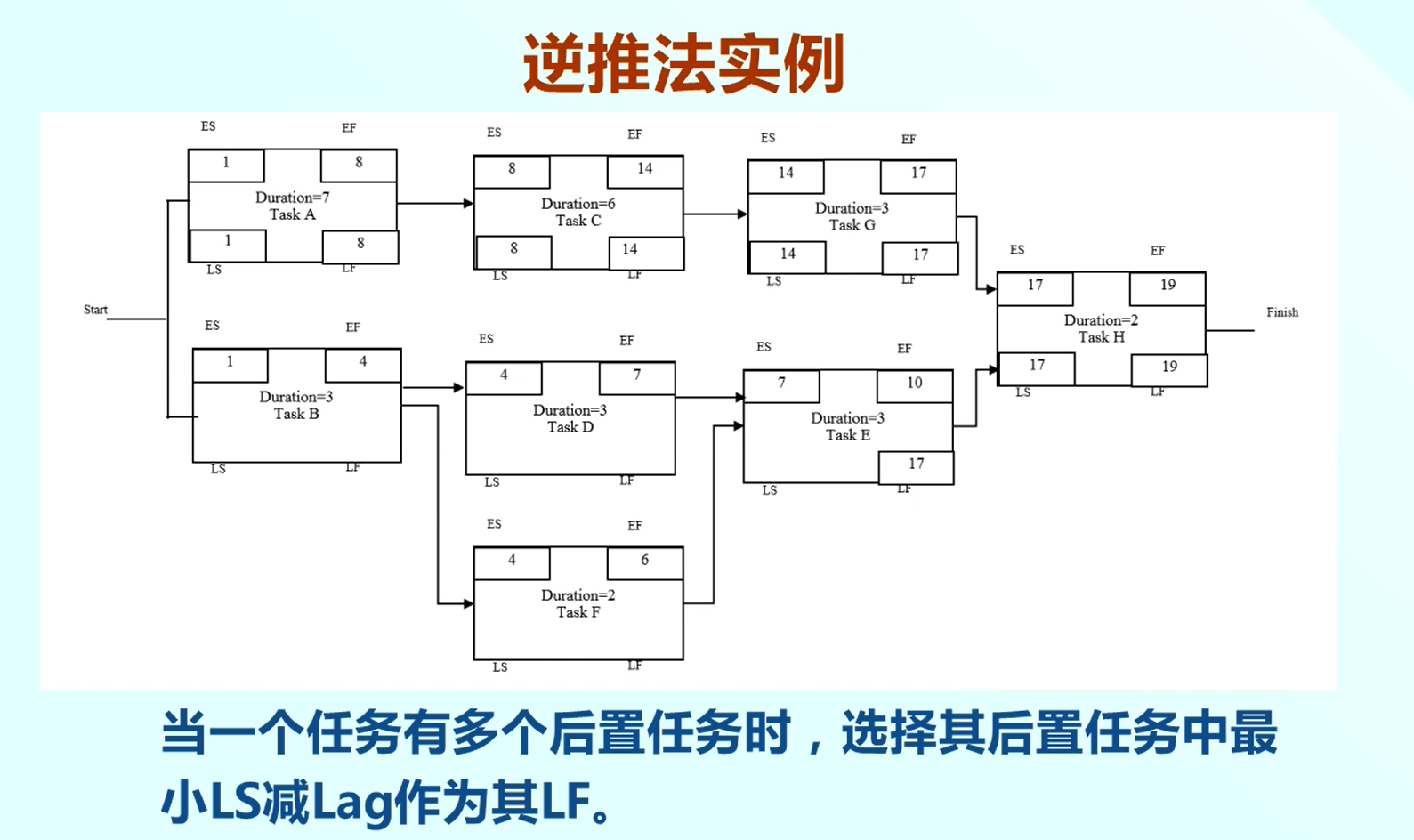
H的最晚結束時間為19，所以LS=17。則前置任務G的LF=17，LS=14，以此類推...自上而下，從右到左。

圖中任務B有兩個後置任務，則需要選擇後置任務中最小的LS減去Lag作為其LF，所以選擇任務D的LS=11,因為沒有Lag，所以任務B的LF=11.

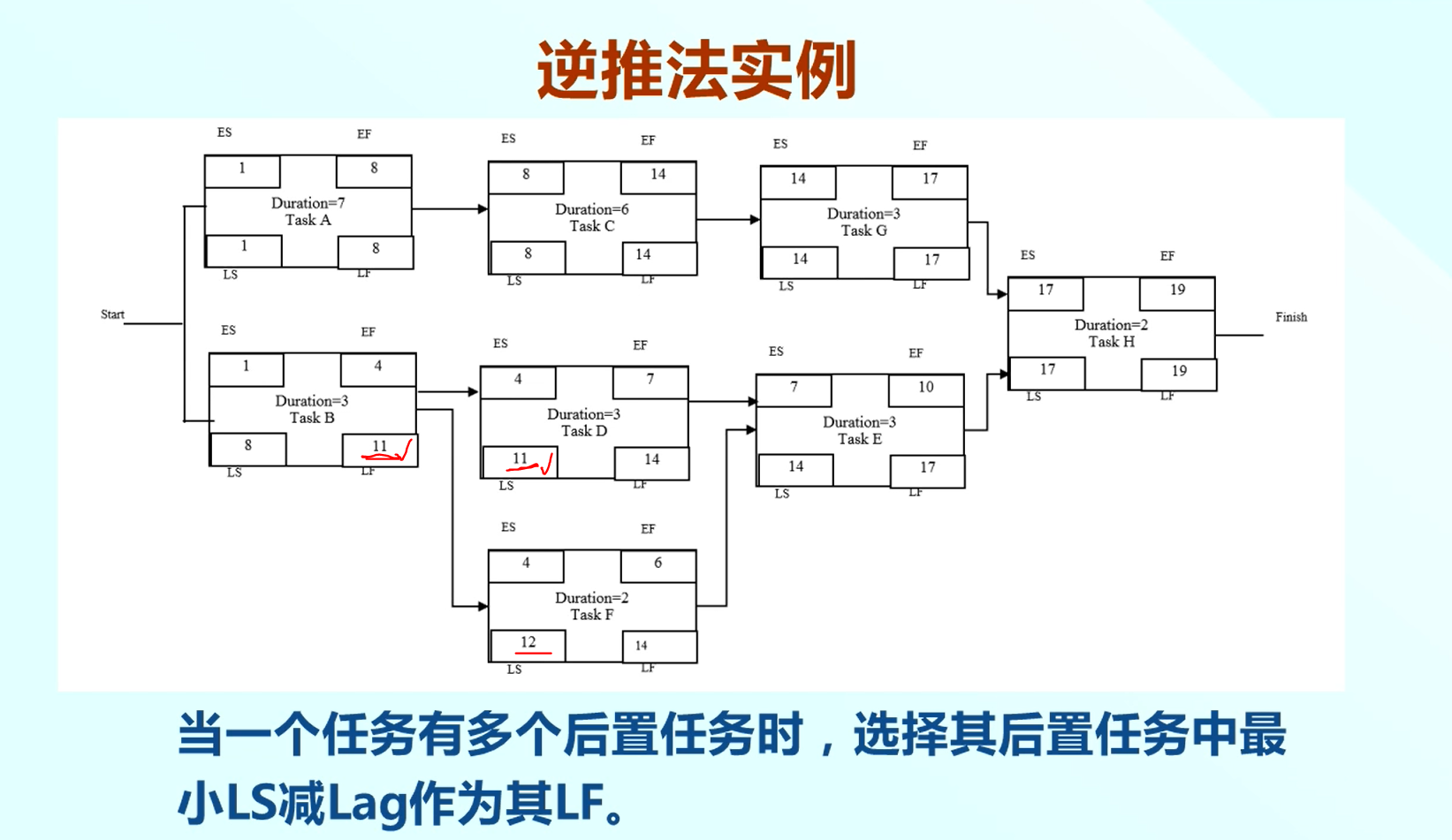
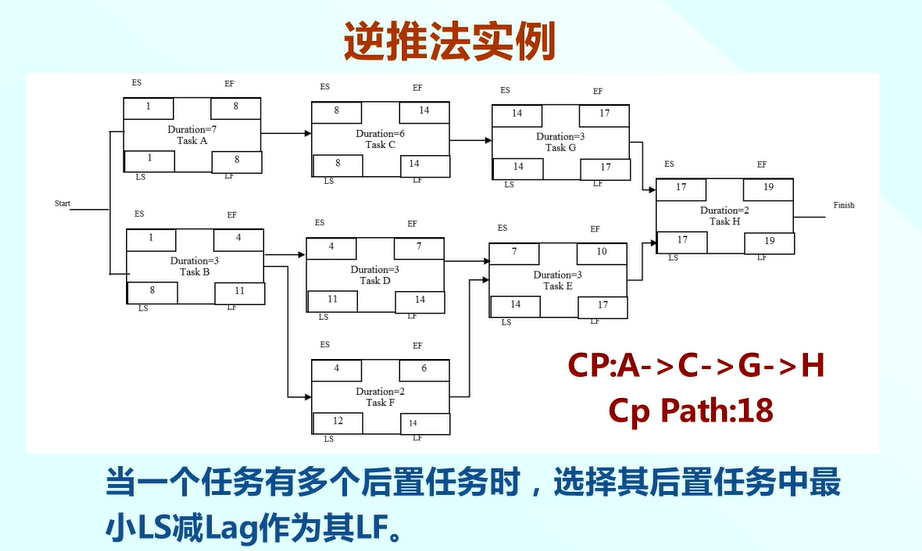
我們繼續看網路圖的關鍵路徑，關鍵路徑是沒有浮動的路徑，是最緊湊的路徑，圖中A->C->G->H是沒有浮動的，所以是關鍵路徑，那麼他也一定是最長的路徑，這個長度是18.

所以通過關鍵路徑確定專案的完成時間是18。

總結

總之 關鍵路徑方法主要是通過正推方法和逆推方法進行任務編排，正推方法確定每個任務的最早開始時間和最早完成時間，逆推方法確定每個任務的最晚完成時間和最晚開始時間。

到這裡，第七章 第四節 第二小節 關鍵路徑法就講解完畢了！下一節介紹時間壓縮法~

如果您覺得這篇文章有幫助到您的的話不妨點贊支援一下喲~~