數值優化：經典一階確定性演演算法及其收斂性分析

我們在上一篇部落格《數值優化：演演算法分類及收斂性分析基礎》介紹了數值優化演演算法的歷史發展、分類及其收斂性/複雜度分析基礎。本篇部落格我們重點關注一階確定性優化演演算法及其收斂性分析。

1 梯度下降法

1.1 演演算法描述

梯度下降法^[1]是最古老的一階方法，由Cauchy在1847年提出。
梯度下降法的基本思想是：最小化目標函數在當前迭代點處的一階泰勒展開，從而近似地優化目標函數本身。具體地，對函數\(f:\mathbb{R}^n \rightarrow \mathbb{R}\)，將其在第\(t\)輪迭代點\(w^t\)處求解下述問題：

\[\underset{w}{\text{min}}f(w) = \underset{w}{\text{min}} \left[ f(w^t) + \nabla f(w^t)^T (w-w^t) \right] \]

上式右端關於自變數\(w\)是線性的，並且使得\(\nabla f(w^t)^Tw\)最小的方向與梯度\(\nabla f(w^t)\)的方向相反。於是梯度下降法的更新規則如下：

\[w^{t+1} = w^t - \eta \nabla f(w^t) \]

其中\(\eta>0\)是步長，也常被稱作學習率。

梯度下降法描述如下：

1.2 收斂性分析

針對不同性質的目標函數，梯度下降法具有不同的收斂速率。由於梯度下降法只適用於梯度存在的函數（沒有梯度需要考慮使用次梯度的方法），這裡考慮梯度下降法對於光滑凸函數和光滑強凸函數的收斂速率。

光滑凸函數收斂性 假設目標函數\(f: \mathbb{R}^d \rightarrow \mathbb{R}\)是凸函數，且\(\beta\)-光滑，當步長\(\eta = \frac{1}{\beta}\)時，梯度下降法具有\(\mathcal{O}(\frac{1}{t})\)的次線性收斂速率：

\[f(w^t) - f(w^*) \leqslant \frac{2\beta \lVert w^0 - w^*\rVert^2}{t} \]

光滑強凸函數收斂性 假設目標函數\(f: \mathbb{R}^d \rightarrow \mathbb{R}\)是\(\alpha\)-強凸函數，且\(\beta\)-光滑，當步長\(\eta = \frac{1}{\beta}\)時，梯度下降法具有\(\mathcal{O}(e^{-\frac{t}{Q}})\)的線性收斂速率：

\[f(w^t) - f(w^*) \leqslant \frac{\beta}{2}e^{-\frac{t}{Q}} \lVert w^0 - w^*\rVert^2 \]

其中\(Q = \frac{\beta}{\alpha}\)，一般被稱為條件數。

通過以上兩個定理可知，強凸性質會大大提高梯度下降法的收斂速率。進一步地，強凸性質越好(即\(\alpha\)越大)，條件數\(Q\)越小，收斂越快。

而光滑性質在凸和強凸兩種情形下都會加快梯度下降法的收斂速率，即\(\beta\)越小（強凸情景下，條件數\(Q\)越小），收斂越快。可以說凸情形中的光滑係數和強凸情形中的條件數在一定程度上刻畫了優化問題的難易程度。

2 投影次梯度下降法

2.1 演演算法描述

梯度下降法有兩個侷限，一是隻適用於無約束優化問題，二是隻適用於梯度存在的目標函數。投影次梯度法^[2]可以解決梯度下降法的這兩個侷限性。

投影次梯度下降法相比梯度下降法，具有次梯度選擇和約束域投影兩個特性：

次梯度選擇 選取當前迭代點\(w^t\)的次梯度集合\(\partial f(w^t)\)中隨機選取一個次梯度\(g^t\)，按照梯度下降更新
\[v^{t+1} = v^t - \eta g^t \]
得到\(v^{t+1}\)。
約束域投影 確定\(v^{t+1}\)是否屬於約束域\(\mathcal{W}\)，如果屬於則直接將其做為\(w^{t+1}\)；如果不屬於，則需尋找\(v^{t+1}\)到約束域\(\mathcal{W}\)的投影，也就是\(\mathcal{W}\)中離\(v^{t+1}\)最近的點。如下圖所示：

尋找投影的過程可以經由投影對映\(\Pi_{\mathcal{W}}(\space \cdot \space)\)來完成：

\[\begin{aligned} w^{t+1} &= \Pi_{\mathcal{W}}(v^{t+1}) \\ &= \underset{v\in \mathcal{W}}{\text{arg min}}\lVert v - v^{t+1}\rVert \end{aligned} \]

投影次梯度下降法描述如下：

2.2 收斂性分析

在一定步長的選取規則下，投影次梯度法是收斂的，並且收斂速度也依賴於目標函數的凸性和光滑性。

對於\(\beta\)-光滑的凸/強凸函數，當步長為\(\frac{1}{\beta}\)時，投影次梯度下降法的收斂率和梯度下降法相同，對於凸函數是\(\mathcal{O}(\frac{1}{t})\)，強凸函數是\(\mathcal{O}（e^{-\frac{t}{Q}}）\)。

不過，由於投影次梯度演演算法適用於有次梯度存在的目標函數，因而不僅適用於光滑函數的優化，也適用於Lipschitz連續函數的優化。對於Lipschitz連續函數，投影次梯度下降法收斂。對於凸函數，步長\(\eta = \mathcal{O}(\frac{1}{\sqrt{t}})\)時，收斂速率為\(\mathcal{O}(\frac{1}{\sqrt{t}})\)；對於強凸函數，步長\(\eta = \mathcal{O}(\frac{1}{t})\)時，收斂速率為\(\mathcal{O}(\frac{1}{t})\)。可以看到其收斂速率在凸和強凸兩種情形相比光滑函數顯著降低，都是次線性。

3 近端梯度下降法

3.1 演演算法描述

近端梯度法^[3]是投影次梯度法的一種推廣，適用於如下形式的部分不可微的凸目標函數的優化問題：

\[\underset{w \in \mathcal{W}}{\text{min}} f(w) = l(w) + R(w) \]

其中\(l(w)\)是其中的可微凸函數部分，\(R(w)\)是不可微的凸函數（例如\(L_1\)正則項）。演演算法的基本思想是先按照可微的\(l\)函數進行一步梯度下降更新：

\[v^{t+1} = w^t - \eta^t \nabla \mathcal{l}(w^t) \]

然後再經過近端對映\(\text{prox}_R(\space \cdot \space)\)做為本輪最終的迭代更新：

\[\begin{aligned} w^{t+1} &= \text{prox}_{R}(v^{t+1}) \\ &= \underset{v\in \mathcal{W}}{\text{arg min}}\left[ R(v) + \frac{1}{2}\lVert v - v^{t+1}\rVert^2 \right] \end{aligned} \]

近端梯度下降法描述如下：

3.2 收斂性分析

如下定理所示，近端梯度下降法可以達到線性收斂速率。

近端梯度下降法收斂性 假設目標函數中的\(l\)函數是\(\mathbb{R}^d\)上的\(\alpha\)-強凸函數，且\(\beta\)-光滑；\(R\)函數是\(\mathbb{R}^d\)上的凸函數，當步長\(\eta = \frac{1}{\beta}\)時，近端梯度下降法具有\(\mathcal{O}(e^{-\frac{t}{Q}})\)的線性收斂速率：

\[f(w^t) - f(w^*) \leqslant \frac{\beta}{2}e^{-\frac{t}{Q}} \lVert w^0 - w^*\rVert^2 \]

其中\(Q = \frac{\beta}{\alpha}\)為\(l\)函數的條件數。

4 Frank-Wolfe演演算法

4.1 演演算法描述

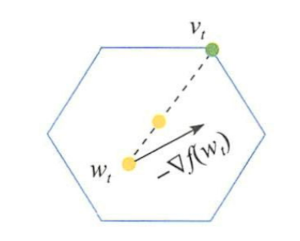
Frank-Wolfe演演算法^[4]是投影次梯度下降法的另一個替代演演算法。投影次梯度演演算法雖然適用於有約束優化問題，但是如果投影的計算很複雜，投影次梯度下降的效率將會稱為瓶頸。為了解決此問題，不同於投影次梯度下降法中先進行梯度下降再對約束域進行投影的做法，Frank-Wolfe演演算法在最小化目標函數的泰勒展開時就將約束條件考慮進去，直接得到滿足約束的近似最小點，即：

\[\begin{aligned} v^t & = \text{argmin}_{v\in\mathcal{W}}\left[ f(w^t) + \nabla f(w^t)^T(v - w^t) \right]\\ & = \text{argmin}_{v\in \mathcal{W}} \nabla f(w^t)^Tv \end{aligned} \]

為了使演演算法的解更穩定，Frank-Wolfe演演算法將求解上述子問題得到的\(v^t\)與當前狀態\(w^t\)做線性加權：

\[w^{t+1} = (1-\gamma^t)w^t + \gamma^tv^t \]

如下圖所示：

Frank-Wolfe演演算法描述如下：

4.2 收斂性分析

Frank-Wolfe演演算法收斂速率如下列定理所示：

Frank-Wolfe法收斂性 假設目標函數中的\(f\)函數是\(\mathbb{R}^d\)上的凸函數，且\(\beta\)-光滑，當加權係數\(\gamma^t = \frac{2}{t+1}\)時，Frank-Wolfe演演算法具有\(\mathcal{O}(\frac{1}{t})\)的次線性收斂速率：

\[f(w^t) - f(w^*) \leqslant \frac{2\beta D^2}{t} \]

其中\(D = \underset{w, v \in \mathcal{W}}{\text{sup}}\lVert w - v \rVert\)。
由於Frank-Wolfe演演算法的收斂速率和投影次梯度下降法相同，可以依據要解決問題中的投影計算是否困難，在兩種演演算法中選擇一種使用。

5 Nesterov加速法

5.1 演演算法描述

考慮以上所有的一階演演算法。在Lipschitz連續的條件下，梯度下降法達到了一階演演算法的收斂速率下界。然而對於光滑函數，一階方法的收斂速率的下界小於梯度下降法的收斂速率。一階方法在凸情形下的收斂率下界為\(\mathcal{O}(\frac{1}{t^2})\)，強凸情形下的下界為\(\mathcal{O}(e^{-\frac{t}{\sqrt{Q}}})\)；而梯度下降法在凸情形下的收斂率為\(\mathcal{O}(\frac{1}{t})\)，強凸情形下的收斂率為\(\mathcal{O}(e^{-\frac{t}{Q}})\)。這說明我們可以針對光滑函數設計收斂速率更快的一階方法。

Nesterov在1983年對光滑度目標函數提出了加快一階優化演演算法收斂的方法^[5]。我們這裡以梯度下降法為例，介紹Nesterov加速法的具體實現。
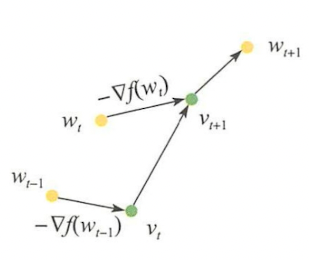
Nesterov演演算法的基本原理如下圖所示：

當任意時刻\(t\)，對當前狀態\(w^t\)進行一步梯度迭代得到輔助變數\(v^{t+1}\)：

\[v^{t+1} = w^t - \eta^t \nabla f(w^t) w^{t+1} \]

然後將新的輔助變數和上一輪迭代計算的輔助變數\(v^t\)做線性加權，做為第\(t+1\)輪迭代的引數\(w^{t+1}\)。對於凸和強凸的目標函數，線性加權係數有所不同。

具體地，對於強凸的目標函數，加權規則如下：

\[w^{t+1} = (1 + \gamma^t)v^{t+1} - \gamma^t v^t \]

其中\(\gamma^t = \frac{1-\sqrt{Q}}{1 + \sqrt{Q}}\)，\(Q\)為條件數。

對於凸的目標函數，加權規則如下：

\[w^{t+1} = (1 - \gamma^t)v^{t+1} + \gamma^t v^t \]

其中\(\gamma^t = \frac{1 - \lambda^t}{\lambda^{t+1}}\)，\(\lambda^0 = 0\), \(\lambda^t = \frac{1 + \sqrt{1 + 4{(\lambda^{t-1})}^2}}{2}\)。

Nesterov加速演演算法描述如下：

5.2 收斂性分析

Nesterov證明了用以上方法加速之後的梯度下降法的收斂速率可以達到針對光滑目標函數的一階方法的收斂速率下界:

光滑凸函數收斂性 假設目標函數\(f: \mathbb{R}^d \rightarrow \mathbb{R}\)是凸函數，並且\(\beta\)-光滑，當步長\(\eta = \frac{1}{\beta}\)時，Nesterov加速法能夠將收斂速率提高到\(\mathcal{O}({\frac{1}{t^2}})\)（不過仍是次線性收斂速率）：

\[f(w^t) - f(w^*) \leqslant \frac{2\beta \lVert w^0 - w^*\rVert^2}{t^2} \]

光滑強凸函數收斂性 假設目標函數\(f: \mathbb{R}^d \rightarrow \mathbb{R}\)是\(\alpha\)-強凸函數，並且\(\beta\)-光滑，當步長\(\eta = \frac{1}{\beta}\)時，Nesterov加速法能夠將收斂速率提高到\(\mathcal{e^{-\frac{t}{\sqrt{Q}}}}\)（不過仍是線性收斂速率）：

\[f(w^t) - f(w^*) \leqslant \frac{\alpha + \beta}{2}e^{-\frac{t}{\sqrt{Q}}} \lVert w^0 - w^*\rVert^2 \]

其中\(Q = \frac{\beta}{\alpha}\)為條件數。

6 座標下降法

6.1 演演算法描述

座標下降法^[6]是另外一種常見的最小化實值函數的方法。其基本思想是，在迭代的每一步，演演算法選擇一個維度，並更新這一維度，其它維度的引數保持不變；或者將維度分為多個塊，每次只更新某塊中的維度，其它維度保持不變。座標下降法的更新公式如下：

\[w^{t+1}_j = \underset{z\in \mathcal{W}_j}{\text{arg min}}f(w^t_1,...,w^t_{j-1}, z, w^t_{j+1},...,w^t_d) \]

其中，\(\mathcal{W}_j\)為第\(j\)個維度塊的約束域。

對於維度的選擇，座標下降法一般遵循以下本徵迴圈選擇規則（Essential Cyclic Rule）：存在一個常數\(r\geqslant d\)，使得對任意的\(s\)，對於每一個維度\(j\)，在第\(s\)輪和第\(s + r - 1\)輪之間都至少選擇一次。最常見的方法是迴圈選擇規則，即對於任意\(j=1,...,d\)，分別在第\(j, d + j, 2d + j,...\)次演演算法迭代中選擇維度\(j\)（即每隔\(d\)輪選擇一次）。

座標下降法的演演算法描述如下所示：

6.2 收斂性分析

可以證明對於強凸並且光滑的目標函數，迴圈座標下降法具有線性的收斂速率^[6]。

參考

[1] Cauchy A. Méthode générale pour la résolution des systemes d’équations simultanées[J]. Comp. Rend. Sci. Paris, 1847, 25(1847): 536-538.
[2]
Levitin E S, Polyak B T. Constrained minimization methods[J]. USSR Computational mathematics and mathematical physics, 1966, 6(5): 1-50.
[3] Parikh N, Boyd S. Proximal algorithms[J]. Foundations and Trends in optimization, 2014, 1(3): 127-239.
[4] Frank M, Wolfe P. An algorithm for quadratic programming[J]. Naval research logistics quarterly, 1956, 3(1‐2): 95-110.
[5] Nesterov Y E. A method for solving the convex programming problem with convergence rate O (1/k^ 2)[C]//Dokl. akad. nauk Sssr. 1983, 269: 543-547.
[6]
Wright S J. Coordinate descent algorithms[J]. Mathematical Programming, 2015, 151(1): 3-34.