Python資料分析--Numpy常用函數介紹(8)--Numpy中幾中常見的圖形

在NumPy中，所有的標準三角函數如sin、cos、tan等均有對應的通用函數。

一、利薩茹曲線

（Lissajous curve）利薩茹曲線是一種很有趣的使用三角函數的方式(示波器上顯示出利薩茹曲線)。利薩茹曲線由以下引數方程定義：

x = A sin(at + n/2)

y = B sin(bt)
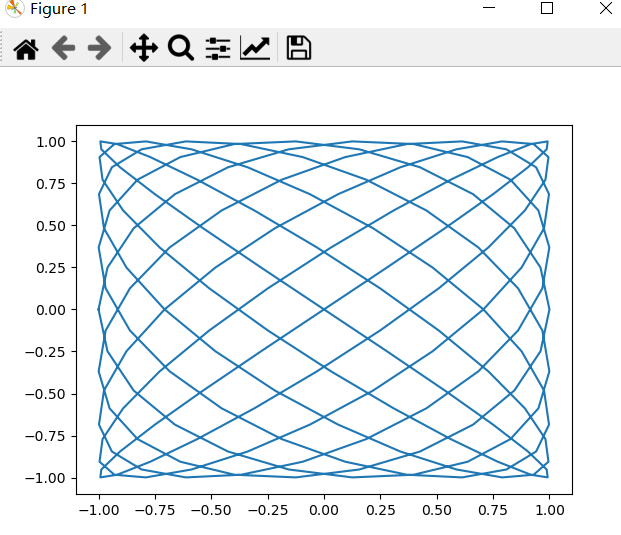
利薩茹曲線的引數包括 A 、 B 、 a 和 b 。為簡單起見，我們令 A 和 B 均為1,設定的引數為 a=9 ， b=8

import numpy as np
import matplotlib.pyplot as plt

A=B=1
a=9
b=8

t = np.linspace(-np.pi, np.pi, 201)  #使用linspace函數初始化變數t
x = np.sin(a * t + np.pi/2)  # sin 函數和NumPy常數 pi 計算變數 x 
y = np.sin(b * t)  # sin函數計算變數y
plt.plot(x, y)
plt.show()

執行結果：

二、計算斐波那契數列

斐波那契數列的遞推關係可以用矩陣來表示。斐波那契數列的計算等價於矩陣的連乘。可用兩種方法計算了斐波那契數列

1）黃金比例計算方法，使用 rint 函數對浮點數取整但不改變浮點數型別

1，1，2，3，5，8，13，21，34，55，89，……

#   斐波那契數,用黃金分割公式或通常所說的比奈公式，加上取整函數
n = np.arange(1, 9)
sqrt5 = np.sqrt(5)
phi = (1 + sqrt5)/2 #利用根號5計算黃金比例，或者直接用phi=1+0.618 
print("比例：",phi)
print('\n')
fibonacci = np.rint((phi**n - (-1/phi)**n)/sqrt5)  #用rint()函數對浮點數取整但不改變浮點數型別
print("Fibonacci", fibonacci)

2）利用矩陣進行計算：用 matrix 函數建立矩陣

# 斐波那契數,用矩陣來表示斐波那契數列的遞推關係
F = np.matrix([[1, 1], [1, 0]])
print ("8th Fibonacci:", (F ** 10)[0, 0])

執行結果：

比例： 1.618033988749895

Fibonacci [ 1.  1.  2.  3.  5.  8. 13. 21.]
8th Fibonacci: 89

三、方波

方波可以近似表示為多個正弦波的疊加。任意一個方波訊號都可以用無窮傅立葉級數來表示。

需要累加很多項級數，且級數越多結果越精確，這裡取 k=99（可以分別設定為9，50，1000等進行測試觀察生成效果）以保證足夠的精度。繪製方波的步驟如下。

1) 初始化 t 和 k 開始，並將函數值初始化為

m = np.linspace(-np.pi, np.pi, 201) #從 -pi 到 pi 上均勻分佈的 201 個點
k = np.arange(1,99)   # k=99 以保證足夠的精度，如圖中的9 20 99顯示的波形
k = 2 * k - 1
f = np.zeros_like(m)

2）使用 sin()求正弦函數，用sum()數計算各項級數：

for i in range(len(m)):  #使用 sin 和 sum 函數進行計算
    f[i] = np.sum(np.sin(k * m[i])/k)
f = (4 / np.pi) * f

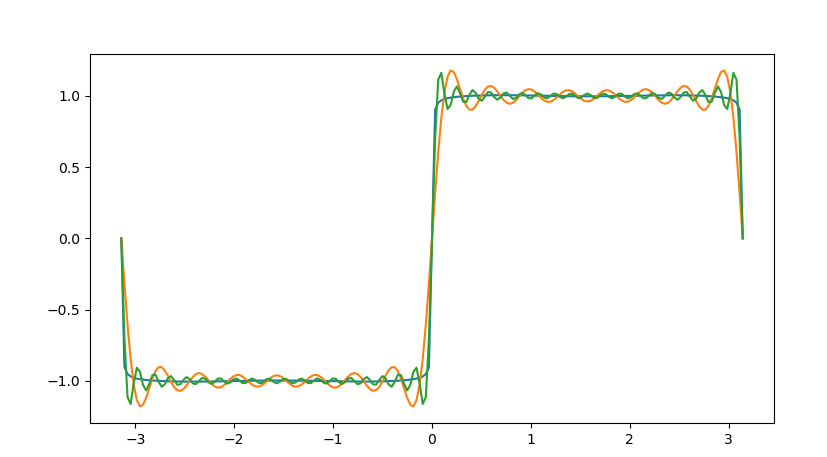
3）繪製波形

plt.plot(t, f)
plt.show()

四、鋸齒波和三角波

鋸齒波和三角波也是常見的波形。和方波類似，也可以將它們表示成無窮傅立葉級數。對鋸齒波取絕對值即可得到三角波。鋸齒波的無窮級數表示式如下：

import numpy as np
import matplotlib.pyplot as plt

t = np.linspace(-np.pi, np.pi, 201)
k = np.arange(1, 99)
f = np.zeros_like(t)
for i in range(len(t)):
    f[i] = np.sum(np.sin(2 * np.pi * k * t[i])/k)

f = (-2 / np.pi) * f
plt.plot(t, f, lw=1.0)
plt.plot(t, np.abs(f), lw=2.0)
plt.show()

執行結果：