技術文章 » 數值優化：演演算法分類及收斂性分析基礎

數值優化：演演算法分類及收斂性分析基礎

2022-06-09 15:03:04

1 優化問題定義

我們考慮以下有監督機器學習問題。假設輸入資料\(D=\{(x_i, y_i)\}_{i=1}^n\)依據輸入空間\(\mathcal{X} \times \mathcal{Y}\)的真實分佈\(p(x, y)\)獨立同分布地隨機生成。我們想根據輸入資料學得引數為\(w\)的模型\(h(\space \cdot\space; w)\)，該模型能夠根據輸入\(x\)給出接近真實輸出\(y\)的預測結果\(h(x; w)\)。我們下面將引數\(w\)對應的模型簡稱為模型\(w\)，模型預測好壞用損失函數\(\mathcal{l}(w; x, y)\)衡量。則正則化經驗風險最小化（R-ERM）問題的目標函數可以表述如下：

\[\hat{l}_n(w) = \frac{1}{n}\sum_{i=1}^n\mathcal{l}(w; x_i, y_i) + \lambda R(w) \]

其中\(R(\space \cdot\space)\)為模型\(w\)的正則項。

由於在優化演演算法的執行過程中，訓練資料已經生成並且保持固定，為了方便討論且在不影響嚴格性的條件下，我們將上述目標函數關於訓練資料的符號進行簡化如下：

\[f(w) = \frac{1}{n}\sum_{i=1}^nf_i(w) \]

其中\(f_i(w)=\mathcal{l}(w, x_i, y_i) + \lambda R(w)\)是模型\(w\)在第\(i\)個訓練樣本\((x_i, y_i)\)上的正則損失函數。
不同的優化演演算法採用不同的方法對上述目標函數進行優化，以尋找最優預測模型。看似殊途同歸，但實踐中的效能和效果可能有很大差別，其中最重要的兩個特性就是收斂速率和複雜度。

2 收斂速率

假設優化演演算法所產生的模型引數迭代序列為\(\{w^t\}\)，其中\(w^t\)為第\(t\)步迭代中輸出的模型引數，R-ERM問題的最優模型為\(w^* = \text{arg min}_w f(w)\)。一個有效的優化演演算法會使序列\(\{w_t\}\)收斂於\(w^*\)。我們用\(w^t\)與\(w^*\)在引數空間中的距離來衡量其接近程度，即

\[\mathbb{E}\lVert w^t - w^*\rVert^2\leqslant \epsilon(t) \]

若用正則化經驗風險的差值來衡量，則為

\[\mathbb{E} [f(w^t) - f(w^*)]\leqslant \epsilon(t) \]

來衡量。
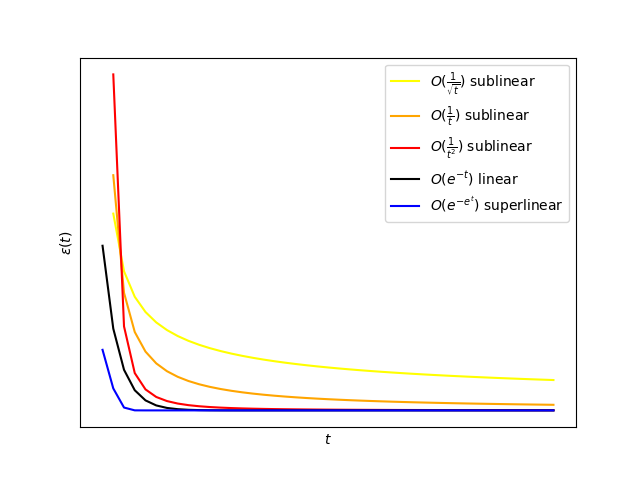
\(\epsilon(t)\)可視為關於\(t\)的函數，收斂的演演算法都滿足隨著\(t\rightarrow \infty\)，有\(\epsilon(t)\rightarrow 0\)，不過其漸進收斂速率各有不同。通常用\(\text{log}\space \epsilon(t)\)的衰減速率來定義優化演演算法的漸進收斂速率。

  • 如果\(\log \epsilon(t)\)與\(-t\)同階，則稱該演演算法具有線性(linear)收斂率。

    例： \(\mathcal{O}(\text{e}^{-t})\)

  • 如果\(\log \epsilon(t)\)比\(-t\)衰減速度慢，則稱該演演算法具有次線性(sublinear)收斂率。

    例： \(\mathcal{O}(\frac{1}{\sqrt{t}})、\mathcal{O}(\frac{1}{t})、\mathcal{O}(\frac{1}{t^2})\)

  • 如果\(\log \epsilon(t)\)比\(-t\)衰減速度快，則稱該演演算法具有超線性(superlinear)收斂率(進一步地，如果\(\log \log \epsilon(t)\)與\(-t\)同階，則該演演算法有二階收斂速率)。

    例：\(\mathcal{O}(\text{e}^{-\text{e}^t})\)

收斂速率各階數對比可參照下圖：

3 複雜度

優化演演算法的複雜度需要考慮單位計算複雜度與迭代次數複雜度。單位計算複雜度是優化演演算法進行單次迭代計算需要的浮點運算次數，如給定\(n\)個\(d\)維樣本，採用梯度下降法來求解模型的單位計算複雜度為\(\mathcal{O}(nd)\)，隨機梯度下降法則是\(\mathcal{O}(d)\)。迭代次數複雜度則是指計算出給定精度\(\epsilon\)的解所需要的迭代次數。比如若我們的迭代演演算法第\(T\)步輸出的模型\(w_t\)與最優模型\(w^*\)滿足關係

\[f(w_t) - f(w^*) \leqslant \frac{c}{\sqrt{t}} \]

，若要計算演演算法達到精度\(f(w^t) - f(w^*) \leqslant \epsilon\)所需的迭代次數，只需令\(\frac{c}{\sqrt{t}}\leqslant \epsilon\)得到\(t \geqslant \frac{c^2}{\epsilon^2}\)，因此該優化演演算法對應的迭代次數複雜度為\(\mathcal{O}(\frac{1}{\varepsilon^2})\)。注意，漸進收斂速率更多的是考慮了迭代次數充分大的情形，而迭代次數複雜度則給出了演演算法迭代有限步之後產生的解與最優解之間的定量關係，因此近年來受到人們廣泛關注。

我們可以根據單位計算複雜度和迭代次數複雜度來得到總計算複雜度，如梯度下降法單位計算複雜度為\(\mathcal{O}(nd)\)，在光滑強凸條件下的迭代次數複雜度為\(\mathcal{O}\left(\log(\frac{1}{\varepsilon})\right)\)，則總計算複雜度為\(\mathcal{O}\left(nd\log{(\frac{1}{\varepsilon})}\right)\)。隨機梯度下降法單位計算複雜度為\(\mathcal{O}(d)\)，在光滑強凸條件下的迭代次數複雜度為\(\mathcal{O}(\frac{1}{\varepsilon})\)，則總計算複雜度為\(\mathcal{O}(\frac{d}{\varepsilon})\)。

4 假設條件

目前大多數優化演演算法的收斂性質都需要依賴目標函數具有某些良好的數學屬性，如凸性和光滑性。近年來由於深度學習的成功人們也開始關注非凸優化問題。我們這裡先討論凸優化的假設。

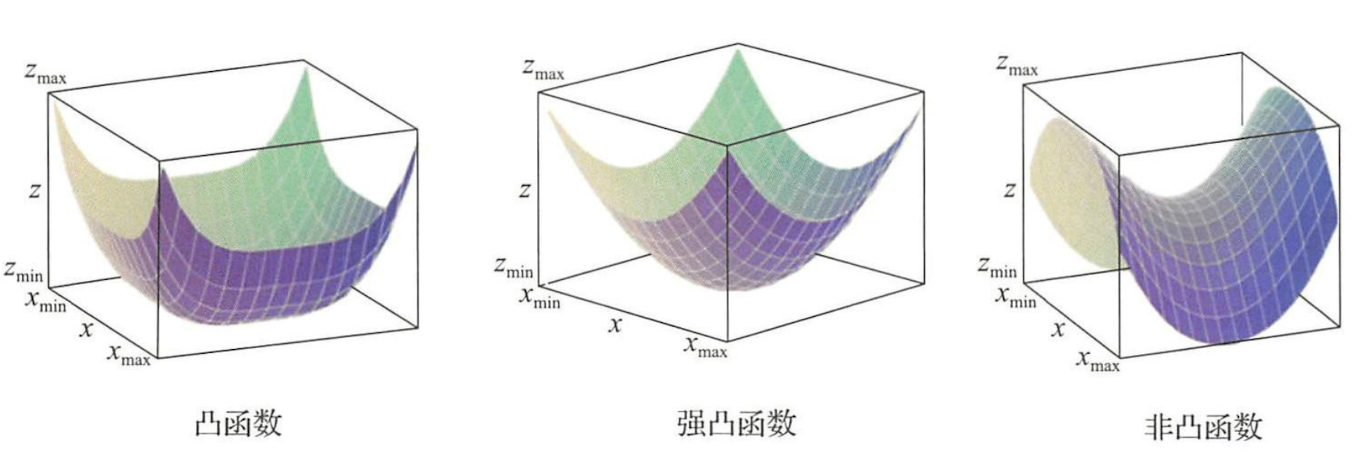
凸函數 考慮實值函數\(f:\mathbb{R}^d\rightarrow \mathbb{R}\)，如果對任意自變數\(w, v \in \mathbb{R}^d\)都有下列不等式成立：

\[f(w) - f(v) \geqslant \nabla f(v)^T(w-v) \]

則稱函數\(f\)是凸的(可以直觀理解為自變數任何取值處的切線都在函數曲面下方)。

凸性會給優化帶來很大方便。原因是凸函數任何一個區域性極小點都是全域性最優解。對於凸函數還可以進一步區分凸性的強度，強凸性質的定義如下：

強凸函數 考慮實值函數\(f:\mathbb{R}^d\rightarrow \mathbb{R}\)和\(\mathbb{R}^d\)上範數\(\lVert \space \cdot \space \rVert\)，如果對任意自變數\(w, v \in \mathbb{R}^d\)都有下列不等式成立：

\[f(w) - f(v) \geqslant \nabla f(v)^T(w-v) + \frac{\alpha}{2} \lVert w - v \rVert^2 \]

則稱函數\(f\)關於範數\(\lVert \space \cdot \space \rVert\)是\(\alpha\)-強凸的。
可以驗證當函數\(f\)是\(\alpha\)強凸的當前僅當\(f - \frac{\alpha}{2} \lVert \space\cdot \space \rVert^2\)是凸的。

下圖中給出了凸函數、強凸函數和非凸函數的直觀形象：

光滑性刻畫了函數變化的緩急程度。直觀上，如果自變數的微小變化只會引起函數值的微小變化，我們說這個函數是光滑的。對於可導和不可導函數，這個直觀性質有不同的數學定義。

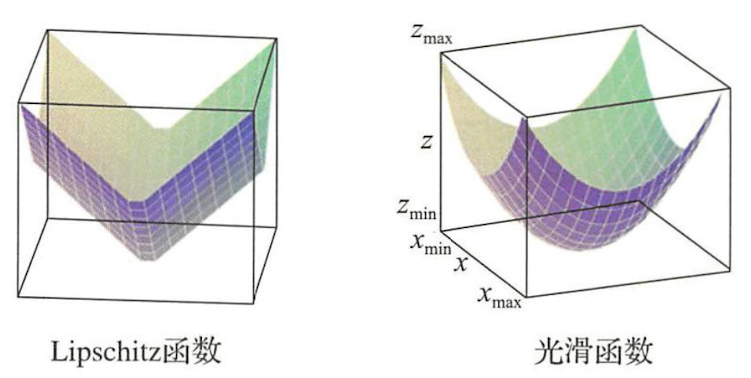
對於不可導函數，通常用Lipschitz性質來描述光滑性。

Lipschitz連續 考慮實值函數\(f:\mathbb{R}^d\rightarrow \mathbb{R}\)和\(\mathbb{R}^d\)上範數\(\lVert \space \cdot \space \rVert\)，如果存在常數\(L>0\)，對任意自變數\(w, v \in \mathbb{R}^d\)都有下列不等式成立：

\[|f(w) - f(v)| \leqslant L \lVert w - v \rVert \]

則稱函數\(f\)關於範數\(\lVert \space \cdot \space \rVert\)是\(L\)-Lipschitz連續的。

對於可導函數，光滑性質依賴函數的導數，定義如下：

光滑函數 考慮實值函數\(f:\mathbb{R}^d\rightarrow \mathbb{R}\)和\(\mathbb{R}^d\)上範數\(\lVert \space \cdot \space \rVert\)，如果存在常數\(\beta>0\)，對任意自變數\(w, v \in \mathbb{R}^d\)都有下列不等式成立：

\[f(w) -f(v) \leqslant \nabla f(v)^T(w-v) + \frac{\beta}{2} \lVert w - v \rVert^2 \]

則稱函數\(f\)關於範數\(\lVert \space \cdot \space \rVert\)是\(\beta\)-光滑的。
下圖是Lipshitz連續函數和光滑函數的直觀形象：

可以驗證，凸函數\(f\)是\(\beta\)-光滑的充分必要條件是其導數\(\nabla f\)是\(\beta\)-Lipschitz連續的。所以，\(\beta\)-光滑函數的光滑性質比Lipschitz連續的函數的光滑性質更好。

5 演演算法分類和發展歷史

數值優化演演算法的發展歷史如下圖所示：

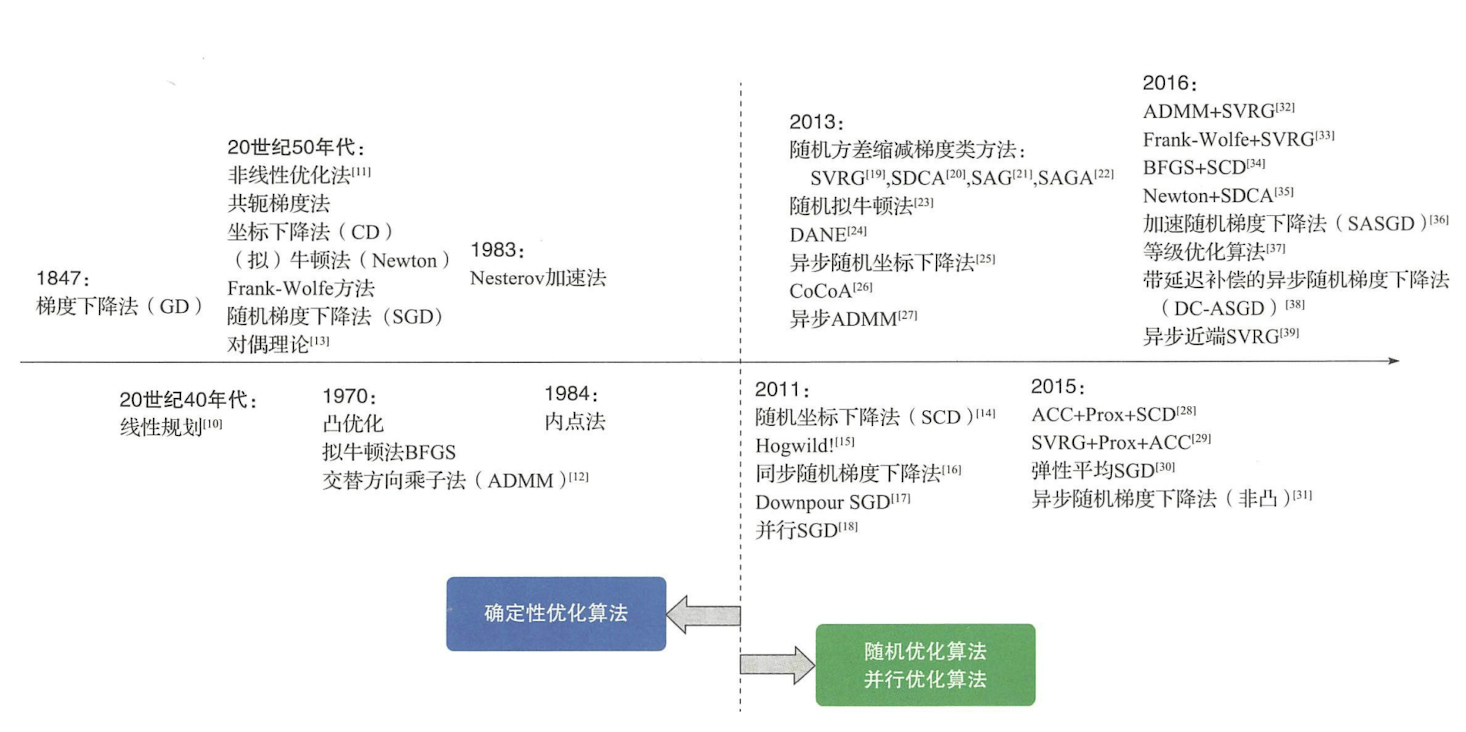
可以看到，優化演演算法最初都是確定性的，也就是說只要初始值給定，這些演演算法的優化結果就是確定性的。不過近年來隨著機器學習中資料規模的不斷增大，優化問題複雜度不斷增高，原來越多的優化演演算法發展出了隨機版本和並行化版本。

為了更好地對眾多演演算法進行分析，我們對其進行了如下分類：

  • 依據是否對資料或變數進行隨機取樣，把優化演演算法分為確定性演演算法和隨機演演算法。
  • 依據演演算法在優化過程中所利用的是一階導數資訊還是二階導數資訊，把優化演演算法分為一階方法和二階方法。
  • 依據優化演演算法是在原問題空間還是在對偶空間進行優化，把優化演演算法分為原始方法和對偶方法。

以上分類可以用下圖加以總結：

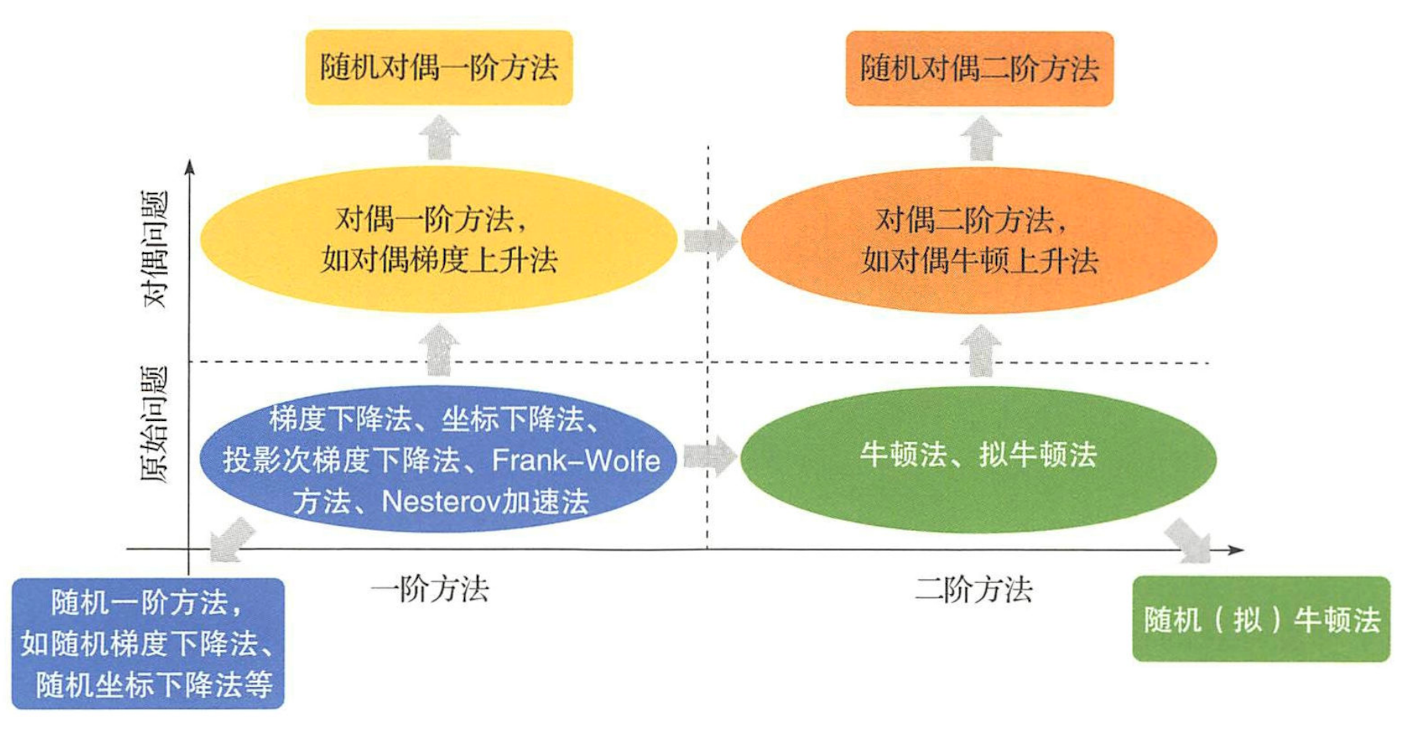
我們下面的部落格將依次討論一階和二階確定性演演算法、單機隨機優化演演算法和並行優化演演算法，大家可以繼續關注。

參考