【學習筆記】計算幾何

基礎知識

向量

概念：有大小和方向的量
基礎演演算法：
（1）加：\((A.x + B.x,A.y + B.y)\)
（2）減：\((A.x - B.x,A.y - B.y)\)
（3）乘常數：\((A.x * k,A.y * k)\)
（4）點積：\(A · B = |A||B|\cos\theta = A.x * B.x + A.y*B.y\)
（5）叉積：\(A \times B = |A||B|\sin\theta = A.x * B.y - A.y*B.x\)

基礎演演算法

（1）旋轉：將 \((x,y)\) 逆時針旋轉 \(\theta\) 就是 \((x * \cos\theta - y * \sin\theta,x * \sin\theta + y * \cos\theta)\)
（2）把向量 \(A\) 轉到與向量 \(B\) 同向：\(B * \dfrac{|A|}{|B|}\)
（3）求多邊形面積：\(\dfrac{1}{2}|\sum_{i=1}^{n-1}P_i \times P_{(i+1)\%n}|\)
（4）以 \(A\) 為原點 \(B\) 為單位點求 \(P\) 的新座標：\((\vec{AB} · \vec{AP},\vec{AB} \times \vec{AP}) * \dfrac{1}{|AB|^2}\)
（5）\(P\) 與直線 \(AB\) 的位置關係：根據 \(\vec{AB} \times \vec{AP}\)
（6）點 \(P\) 在直線 \(AB\) 上的投影：\(A + \dfrac{\vec{AB} * (\vec{AB} · \vec{AP})}{|AB|^2}\)
（7）點與線段的位置關係：判斷與線段所在直線的位置關係、點積判斷在哪裡
（8）\(AB \mathop{//} CD：\vec{AB} \times \vec{CD} = 0\)
（9）直線 \(AB\) 和直線 \(CD\) 求交點：\(A + \vec{AB} * \dfrac{\vec{CD}\times\vec{CA}}{\vec{AB} \times \vec{CD}}\)
（10）線段與直線求交點：線段兩端點在直線兩側、直線求交點

凸包

Graham 掃描法

求凸包：
（1）找到所有的點中最左下角的點，並加入棧中
（2）將所有點按極角排序逆時針
（3）每次找到一個點，判斷該點是否在最後這條邊的右邊，若是則彈出棧頂，直到不能彈出就加入棧裡
求下凸殼：
按橫座標從小到大排序，然後執行上文 （3）
求上凸殼：
按橫座標從大到小排序，然後執行上文（3）

旋轉卡殼

本質：固定一個點，所求與另一個點的位置呈單峰函數且峰值關於固定點單調的演演算法

例題：

題目描述：
求解凸多邊形的直徑。直徑的定義為凸多邊形上兩點間距離的最大值。
解法：
（1）任意選擇一個點為固定點
（2）以固定點在逆時針順序下的下一個點為第二個點
（3）因為這兩點間的距離與第二個點的位置呈單峰函數，且峰值關於固定點單調，所以就按逆時針方向移動第二個點
（4）移動到最大距離處，計算貢獻，並按逆時針方向移動固定點，不移動第二個點
（5）重複（3）直到移動結束
例如下圖所示：

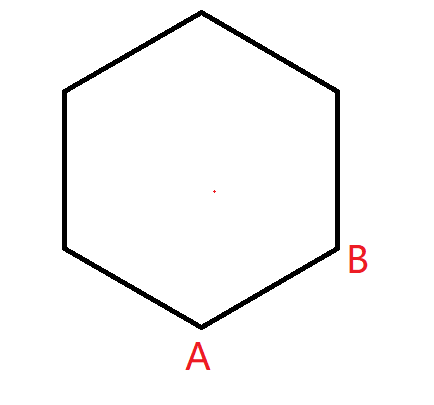
先隨機找到固定點 \(A\)，與對應的第二個點 \(B\)

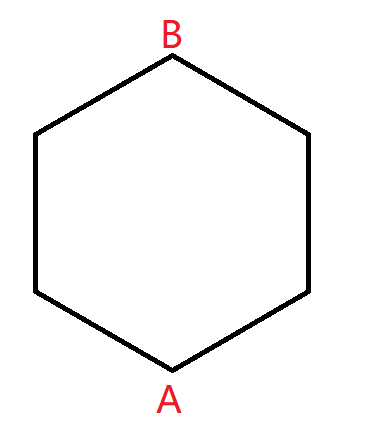
移動 \(B\) ，使得 \(A\) 與 \(B\) 兩點間距離最大

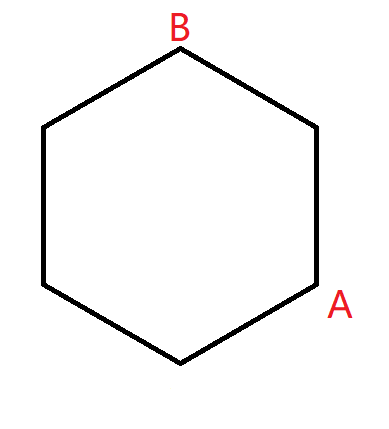
保持 \(B\) 不動，移動 \(A\)
然後再按照上文的方法一直迴圈執行

圓

點與圓

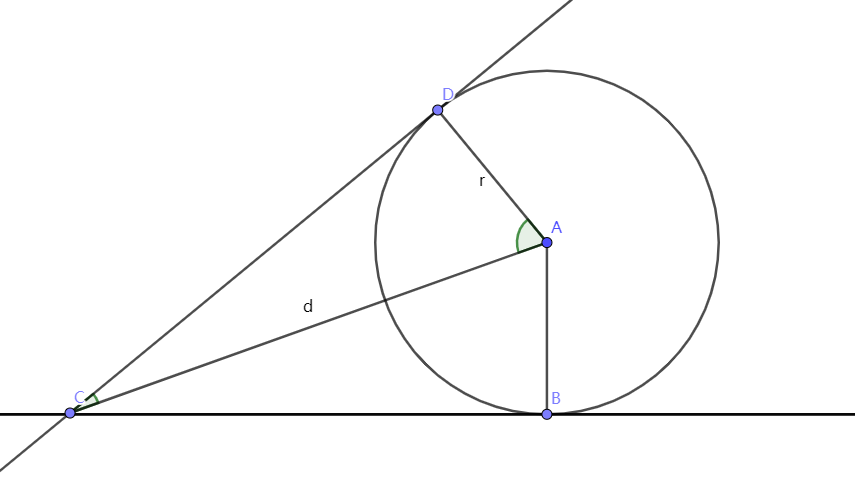
判斷點是否在圓上： \(d \le r\)
\(d = |PC|,r = r\) \(\angle DAC = \arccos(\dfrac{r}{d}),\angle DAC = (\arcsin\dfrac{r}{d})\)

直線與圓

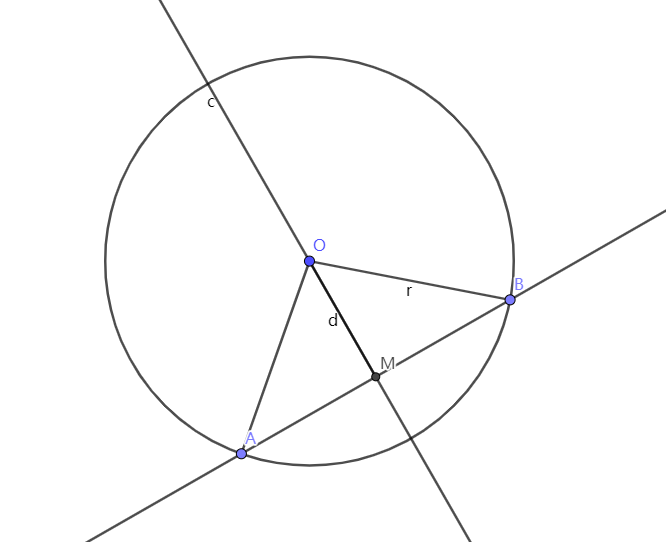
根據叉積得到 \(d\)
\(|MA| = |MB| = \sqrt{r^2 - d^2}\)，\(\angle OBM = \arccos \dfrac{d}{r}\)

圓與圓

是否相交

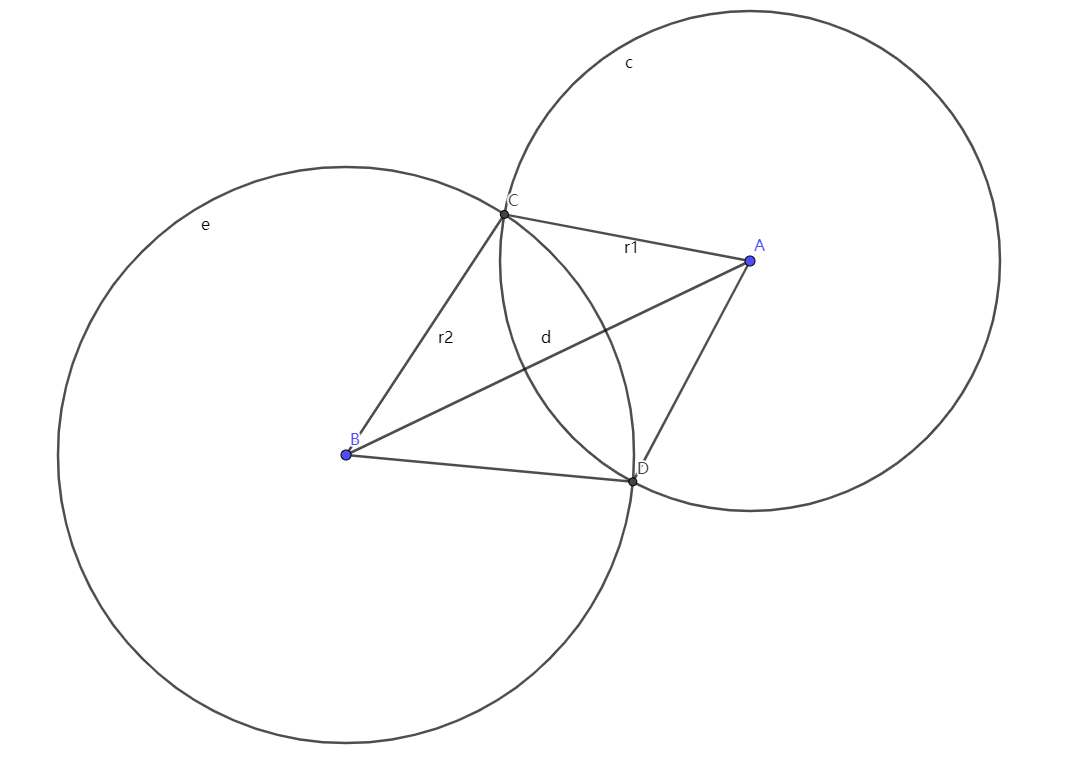
根據 \(d\) 與 \(r_1 + r_2\)

不交圓外公切線

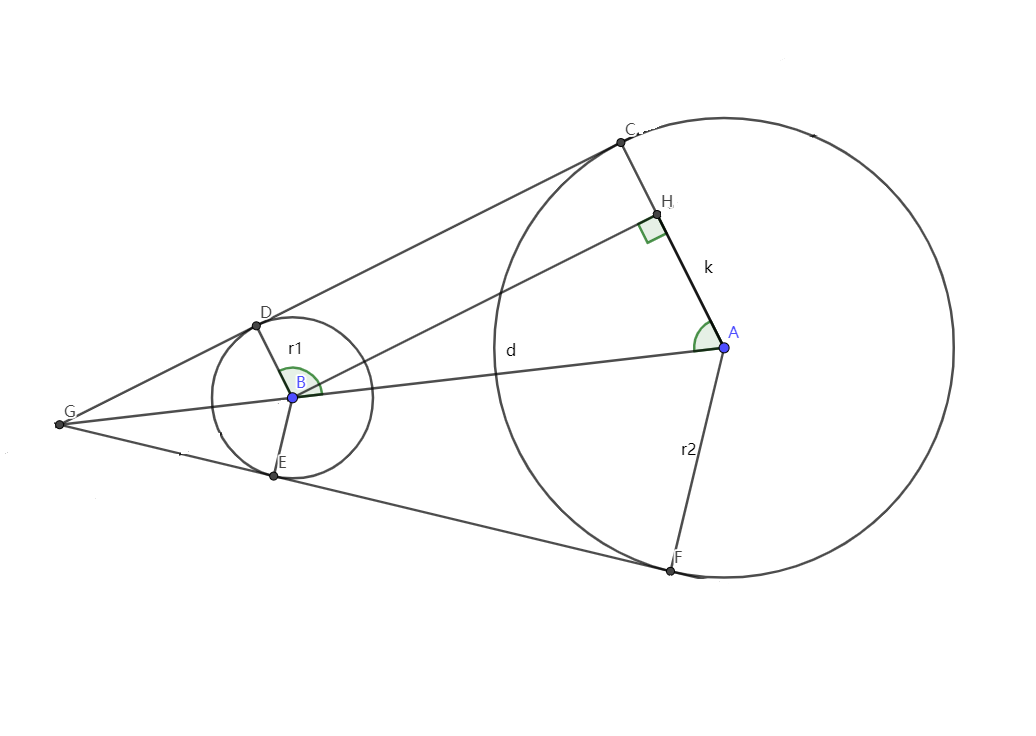
\(k = r_2 - r_1 , \angle CAB = \arccos \dfrac{r2-r1}{d},\angle DBA = \arccos \dfrac{r_1-r_2}{d}\)

不交圓內公切線

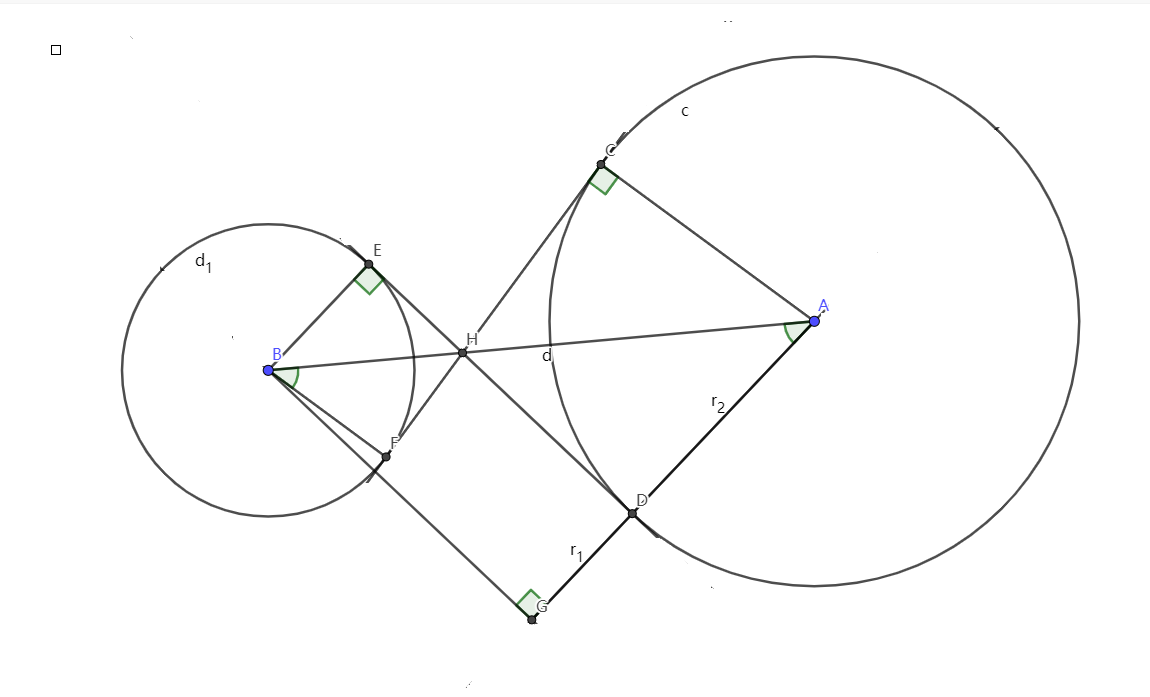
\(\angle BAG = \angle ABF = \arcsin \dfrac{r_1+r_2}{d}\)