每個開發都應該懂的正規表示式

在日常工作中，相信每個開發都接觸過一些檢索、替換字串/文字的問題。對於一些簡單的問題例如查詢字串中是否存在某個子串，可能直接使用各類開發語言自帶的 api 介面就可以很方便地實現。但是一旦規則複雜起來可能就會比較棘手，例如校驗郵箱、手機號、版本號等，如果自行實現可能需要寫不少邏輯程式碼，正規表示式就是為了解決這類問題的。舉個例子，以下是 CI 構建元件時對版本號的校驗，你能夠快速讀懂其規則嗎？如果你對此不甚瞭解，那相信這篇文章一定能給你帶來一些收穫。

什麼是正規表示式

如上圖所示，正規表示式就是一串字元/^[0-9]+.[0-9].+[0-9]+$/，正規表示式規定了由一個或幾個特殊的字元組合成一個規則，並且多個規則可以自由組合。

在學習正規表示式時，不要被表示式裡的特殊符號所迷惑，覺得看起來好複雜，其實說白了這些字元只是一些規則的對映而已，並且需要注意的是，如果字串裡使用到這些符號還需要跳脫。

常見的字元有 * . ? + ^ - $ | \ / [ ] ( ) { }。另外有的開發語言在使用時需要將正規表示式使用 / 符號抱起來，形如 /xxx/，這個瞭解下即可。

既然正規表示式由一系列規則組成，每個規則都描述了一套匹配的邏輯，那麼學習正規表示式其實就是在學習這些匹配規則。讓我們先從最直觀的匹配字元開始入手。在開始之前，推薦大家兩個網站，一個是用於測試的正規表示式規則測試，一個正規表示式圖形化工具，便於我們理解。

匹配字元

精確匹配

例如從 abcde 裡尋找 abc，那麼很明顯，我們的匹配規則就是需要精確匹配 abc，其規則自然就是 abc。這個不多贅述。

模糊匹配

除了精確匹配以外，我們可能還需要一些模糊的規則，以便於發現/容納更多可能。比如我們需要某處的字元是可變的，或者我們對於某處的字元數量不確定。因此就產生了橫向和縱向兩種字元模糊匹配。

橫向（字元次數匹配）

某處的字元數量可變，可以使用次數匹配規則。

常見的次數匹配規則有：

{n}：限定n次
{m,n}：上下限次數（閉區間）
+：一次或多次，等效於 {1,}
？：零次或一次，等效於 {0,1}
*：任意多次

這些規則跟在某個字元后面，代表規則前面的字元長度可變。

例如正規表示式： a{2,3}c，代表 a 字元出現2次或3次，例如 aac、aaac 都是可以匹配的。但是 ac 是無法匹配的。

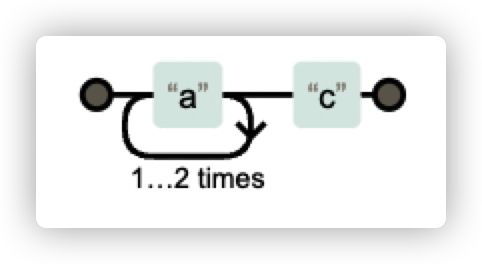
縱向

某處的字元可變，比如需要匹配 dog 和 log。第一個字元有多種可能。

常見的字元可變規則有：

. ：點代表任意字元
| ：或匹配。可以配合 () ，將多個子表示式組合
[]：區間裡的字元都是允許的，例如 [123]，代表該處的字元可以是 1 或 2 或 3
-：區間裡使用，表示範圍，例如 [1-3] 等同於 [123]，[a-z] 代表所有小寫英文字母
^：區間裡使用，表示取反，例如 [^1-3] 代表除了 1、2、3 以外的字元
這些規則放在某處，代表某處的字元是可變的。

例如 [dl]og ，代表中括號處（第一個字元）可以是 d 或 l，因此 log、dog 都是可以匹配的

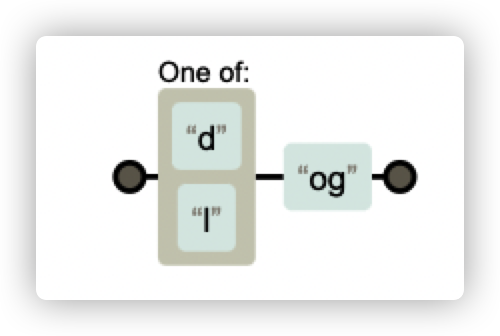
除此之外，還會有一些常用的簡寫：

\d：數位
\D：非數位
\w：數位大小寫下劃線，等同於 [0-9a-zA-Z_]
\W：非單詞字元，等同於 [^0-9a-zA-Z_]
\s：空白字元，包括空白、tab、換行

匹配位置

一個字串，除了我們最直觀看到字元以外，其實還暗含了許許多多的位置。這也是正則匹配的另一大塊。什麼是位置？首先用一張圖來表示：

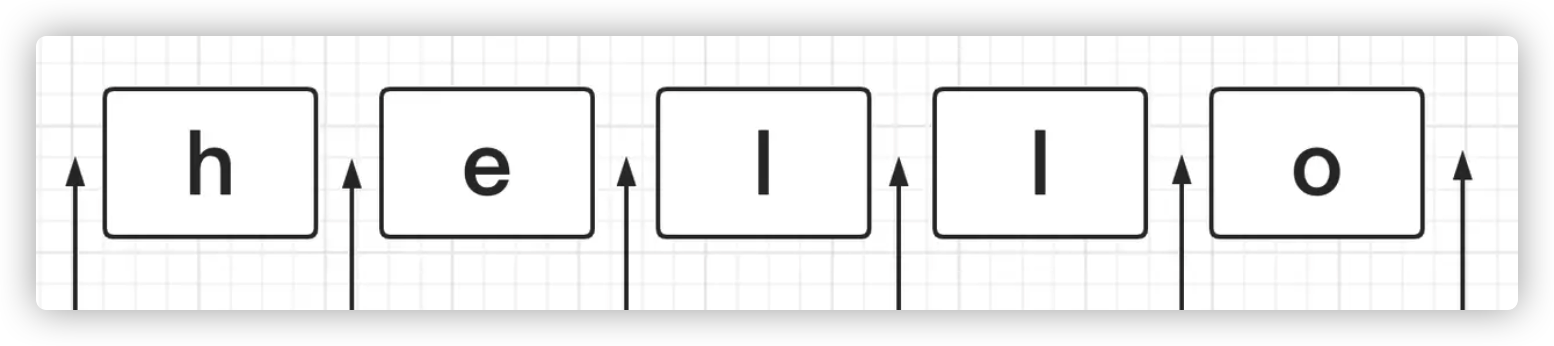
如圖所示，一個字串 hello，除了五個字元以外，每個字元首尾都有一個位置，這些位置都可以被匹配規則所掃描到。

常用的匹配位置的符號有：

^ ：代表一行的開頭
$ ：代表一行的結尾
\b：單詞邊界。具體就是單詞字元和非單詞字元之間的位置。包括非單詞字元和開頭、結尾之間的位置
\B：非單詞邊界

可能有人對匹配位置的用法不太瞭解，舉個例子，有一個字串 123123，這時候如果你使用精確匹配規則 123，那麼會匹配到兩個123。但是如果配合 ^ 使用，將規則修改為 ^123，那麼就只會匹配到第一個開頭的 123，後續的 123 則不會被匹配到。

除此之外，關於匹配位置還有一個很靈活的特性：前瞻後顧

相關的規則有：

exp1(?=exp2)：前瞻，查詢後面是exp2的exp1 = 查詢exp2前面的exp1（exp1、exp2 代表一個表示式）
(?<=exp2)exp1：後顧，查詢exp2後面的exp1
exp1(?!exp2)：負前瞻，查詢後面不是exp2的exp1
(?<!exp2)exp1：負後顧：查詢前面不是exp2的exp1

這個在過濾紀錄檔時十分有用。例如有一些重複關鍵字的紀錄檔：

receive some error
receive yuv
receive yuv
receive yuv
receive yuv

//receive(?! yuv)
可以使用負前瞻過濾掉一些不想要的紀錄檔。只會匹配到 receive some error 這一行的 rece

實際應用

在對正規表示式有個大致的認識後，讓我們回到文章的開頭，看一下文章開頭的版本號驗證正規表示式代表什麼含義：^[0-9]+.[0-9].+[0-9]+$

這裡可以明顯看出是有問題的，例如表示式裡的 . 應該需要跳脫，否則就代表任意字元，這明顯不符合版本號要求。經過確認後得知是前端顯示問題，並瞭解到他們實際校驗使用的正規表示式是：^\d+\.\d+\.(\d+\.)*\d+((-rc\.\d+)|(\d*))$

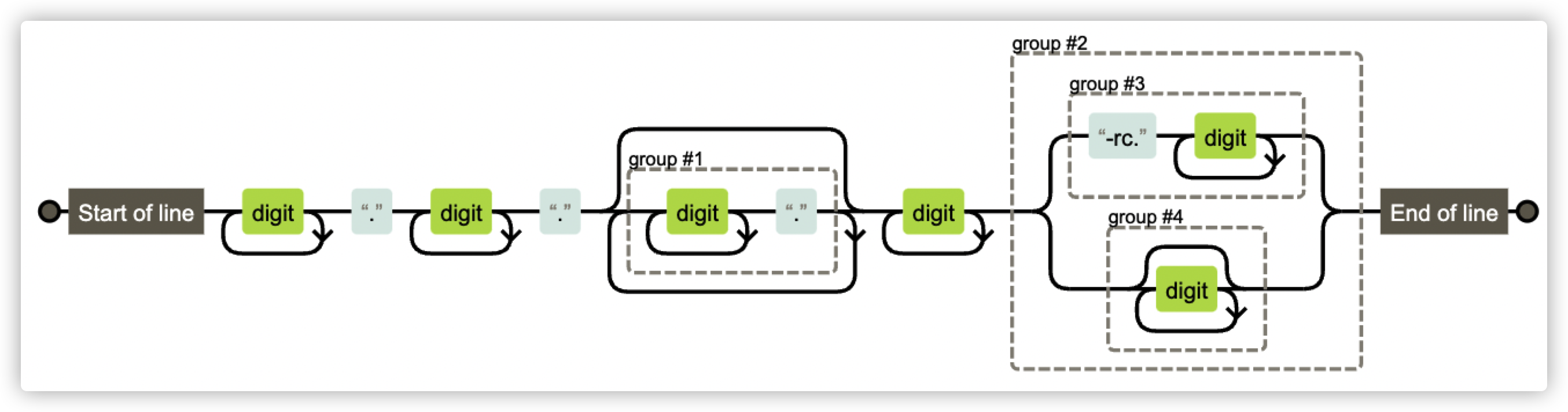
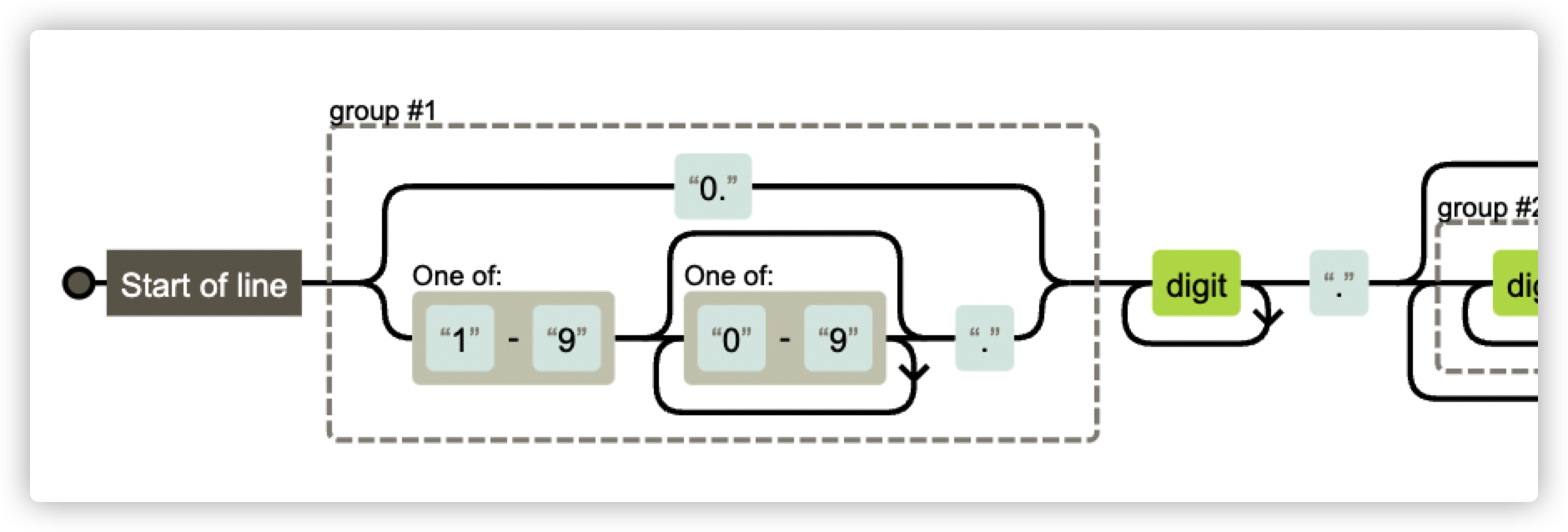
在對正則規則有個大致瞭解後，藉助圖形化工具可以很方便地瞭解正規表示式規則所代表的含義。
例如 1.1.1.1.1 這樣的版本號也是允許的，經瞭解 CI 之前有特殊原因沒限制版本號一定是 3 位。並且可以看到除了 rc 字元以外，不允許其他英文字母。
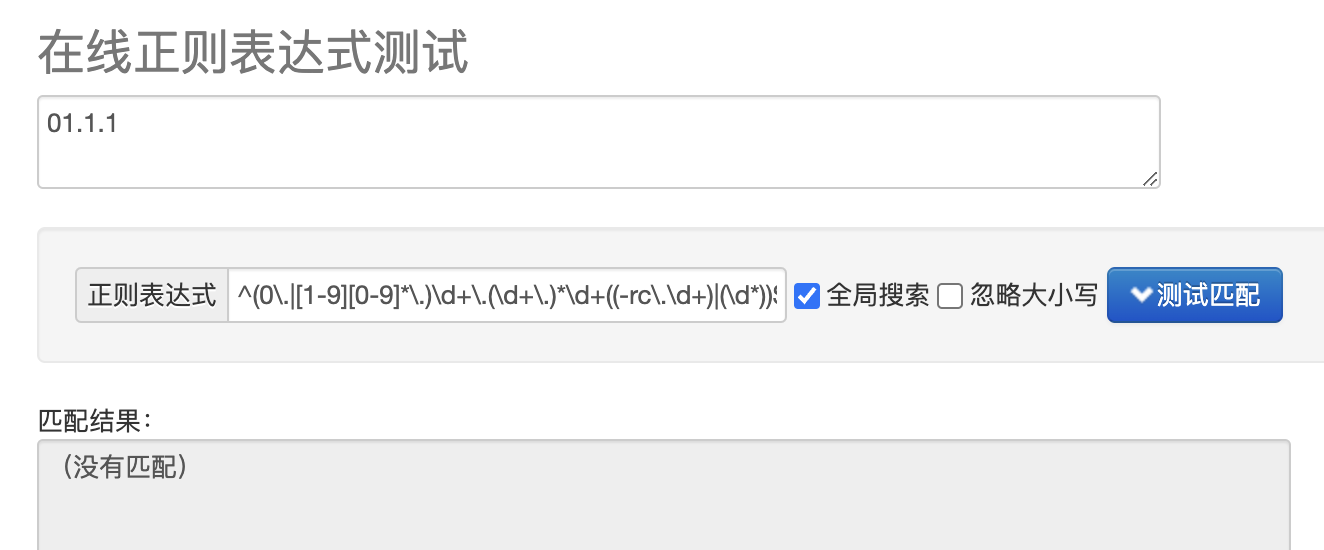
但同時我們也會發現另一個小問題，那就是類似 01.1.1 這樣的版本號也是被允許的：
如果讓你來優化會怎麼做呢？我認為優化後的規則可以這麼寫：^(0\.|[1-9][0-9]*\.)\d+\.(\d+\.)*\d+((-rc\.\d+)|(\d*))$。
使用(0\.|[1-9][0-9]*\.)限制要麼是0，要麼是非0的兩位以上數位，即可過濾 01.1.1 這樣的不合理版本號。

相信看到這裡，大家都對正規表示式有了一個大致的瞭解。對於正規表示式還有一些特性（例如捕獲、貪婪等）沒有提及，這裡拋磚引玉，感興趣的小夥伴可以自行了解。
有了正規表示式的幫助可以讓我們少寫很多字串判斷邏輯的程式碼，除了讓程式碼更簡潔以外，也會大大提高程式碼的可讀性。