Python資料分析--Numpy常用函數介紹(6)--Numpy中與股票成交量有關的計算
成交量(volume)是投資中一個非常重要的變數,它是指在某一時段內具體的交易數,可以在分時圖中繪製,包括日線圖、周線圖、月線圖甚至是5分鐘、30分鐘、60分鐘圖中繪製。
股票市場成交量的變化反映了資金進出市場的情況,成交量是判斷市場走勢的重要指標。一般情況下,成交量大且價格上漲的股票,趨勢向好。成交量持續低迷時,一般出現在熊市或股票整理階段,市場交易不活躍。成交量是判斷股票走勢的重要依據,對分析主力行為提供了重要的依據。投資者對成交量異常波動的股票應當密切關注。
OBV(On-Balance Volume,淨額成交量或叫能量潮指標)是最簡單的股價指標之一,它可以由當日收盤價、前一天的收盤價以及當日成交量計算得出。以前一日為基期計算當日的OBV值(可以認為基期的OBV值為0)。若當日收盤價高於前一日收盤價,則本日OBV等於基期OBV加上日成交量。若當日收盤價低於前一日收盤價,則本日OBV等於基期OBV減去當日成交量。若當日收盤價相比前一日沒有變化,則當日成交量以0計算。
一、OBV計算
鑑於上述計算方法,需要在成交量前面乘上一個由收盤價變化決定的正負號(收盤價低於前一交易日收盤價,負號,收盤價高於前一交易日收盤價,正號)。在本篇中,學習該問題的兩種解決方法,一種是使用NumPy中的 sign 函數,另一種是使用NumPy的piecewise 函數。
1) 把資料分別載入到收盤價和成交量的陣列中:
close,vol = np.loadtxt('data036.csv',delimiter=',', usecols=(5,6),converters={1:datestr2num},unpack=True)
data036.csv中的第6列和第7列分別為收盤價和當日成交量。
前篇介紹過numpy.diff()可以計算相鄰的差(即上述收盤價close的差值),並利用這個差值, 用sign 函數計算正負號
changes = np.diff(close) signs = np.sign(changes) print ("Signs", signs)
執行結果:
Signs [-1. -1. -1. -1. 1. 1. 1. -1. 1. 1. 1. -1. 1. -1. -1. -1. -1. 1. 1. -1. -1. 1. 1. 1. 1. 1. 1. 1. -1. 1. 1. 1. -1. -1. -1. 1. -1. 1. 1. 1. -1. -1. 1. 1. 1. -1. -1. 1. 1. 1. 1. 1. 1. -1....
2)也可以使用 piecewise 函數來獲取陣列元素的正負。 piecewise函數可以分段給定取值。使用合適的返回值和對應的條件呼叫該函數:
pieces = np.piecewise(changes, [changes < 0, changes > 0], [-1, 1]) print("Pieces", pieces)
3)判斷是否 sign 函數和piecewise 函數計算結果是否一致用array_equal()函數:
print ("Arrays equal?", np.array_equal(signs, pieces))
執行結果:
Arrays equal? True
4)由於diff()y計算的結果是相鄰資料相減,因此得到419個資料,較從檔案中匯入的資料420個少一位,因此無法計算首日的OBV值
obv_values = vol[1:] * signs #計算obv值 print("obv values:",obv_values[:20]) #列印前20個obv值
完成程式碼如下:
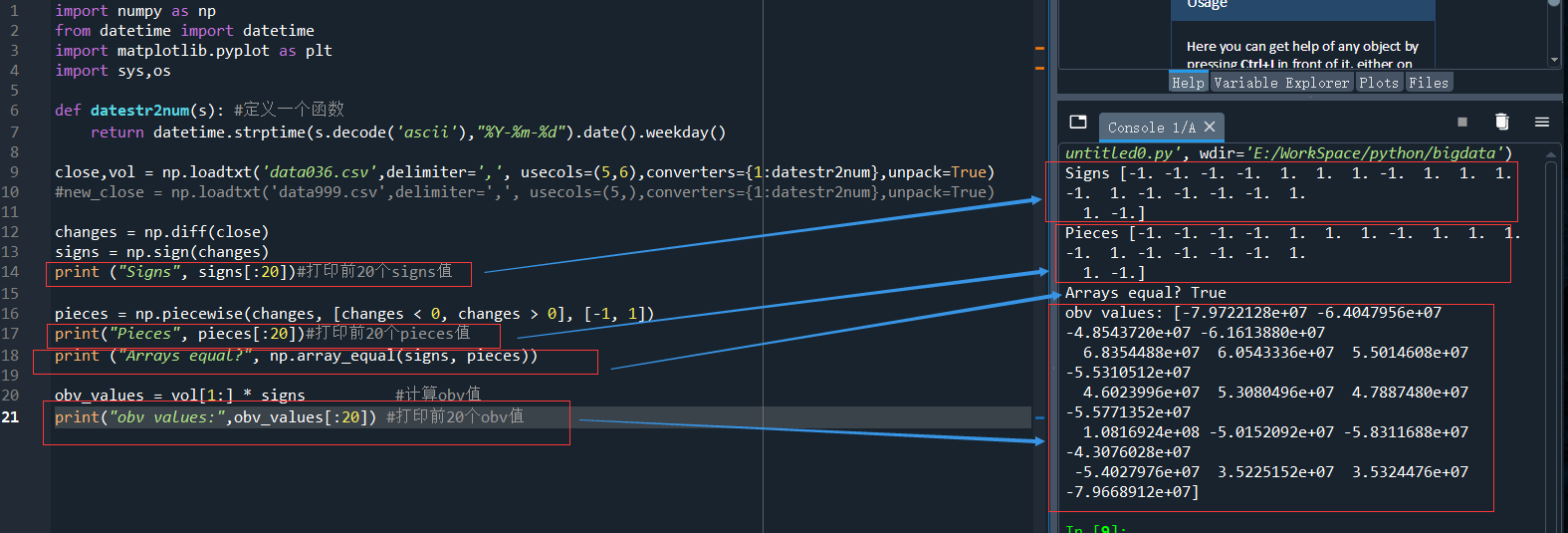
import numpy as np from datetime import datetime import matplotlib.pyplot as plt import sys,os def datestr2num(s): #定義一個函數 return datetime.strptime(s.decode('ascii'),"%Y-%m-%d").date().weekday() close,vol = np.loadtxt('data036.csv',delimiter=',', usecols=(5,6),converters={1:datestr2num},unpack=True) #new_close = np.loadtxt('data999.csv',delimiter=',', usecols=(5,),converters={1:datestr2num},unpack=True) changes = np.diff(close) signs = np.sign(changes) print ("Signs", signs[:20])#列印前20個signs值 pieces = np.piecewise(changes, [changes < 0, changes > 0], [-1, 1]) print("Pieces", pieces[:20])#列印前20個pieces值 print ("Arrays equal?", np.array_equal(signs, pieces)) obv_values = vol[1:] * signs #計算obv值 print("obv values:",obv_values[:20]) #列印前20個obv值
執行結果:
二、 計算單個交易日的利潤
1)讀入資料
將所有交易資料(開盤價、收盤價、最高價、最低價,成交量等)載入到對應的陣列中
import numpy as np from datetime import datetime import matplotlib.pyplot as plt import sys,os def datestr2num(s): #定義一個函數 return datetime.strptime(s.decode('ascii'),"%Y-%m-%d").date().weekday() opens,highs,lows,closes,vols = np.loadtxt('data036.csv',delimiter=',', usecols=(2,3,4,5,6),converters={1:datestr2num},unpack=True) #開盤價、最高價、最低價、收盤價、成交量陣列。
2)呼叫 vectorize 函數並給定calc_profit 函數作為引數:
(1)先定義一個計算利潤的函數:這個函數,是以開盤價買入,以當日收盤價賣出,所獲得的利潤即買入和賣出的差價。事實上,計算相對利潤更為直觀。
def calc_profit(opens, highs, lows, closes): buy = opens * 1 if lows < buy < highs : return (closes - buy)/buy else: return 0
(2)呼叫 vectorize 函數並給定calc_profit 函數作為引數
func = np.vectorize(calc_profit) profits=func(opens,highs,lows,closes) print ("Profits", profits)
3)選擇非零利潤的交易日,並計算平均值:
real_trades = profits[profits != 0] print ("Number of trades", len(real_trades), round(100.0 * len(real_trades)/len(closes), 2),"%") print ("Average profit/loss %", round(np.mean(real_trades) * 100, 2))
當然也可以分別計算盈利和虧損:
real_trades = profits[profits > 0] print ("Number of trades", len(real_trades), round(100.0 * len(real_trades)/len(closes), 2),"%") print ("平均盈利: %", round(np.mean(real_trades) * 100, 2)) loss_trades = profits[profits < 0] print ("Number of trades", len(loss_trades), round(100.0 * len(loss_trades)/len(closes), 2),"%") print ("平均虧損 %", round(np.mean(loss_trades) * 100, 2))
實際執行結果:
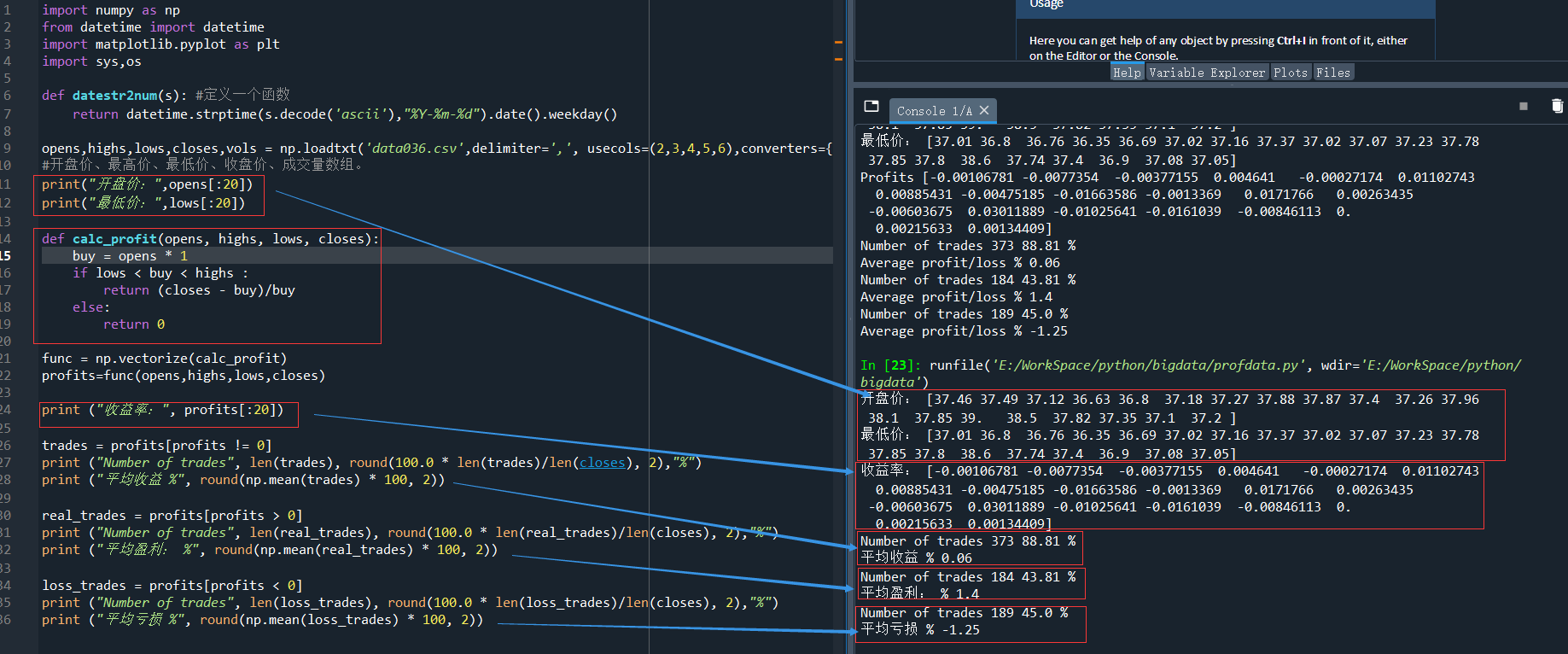
三、資料平滑
噪聲資料很難處理,因此需要對其進行平滑處理,除前篇介紹的計算移動平均線的方法,還可以使用NumPy中的一個函數來平滑資料。hanning 函數是一個加權餘弦的窗函數。
1)呼叫 hanning 函數計算權重,生成一個長度為 N 的視窗(在這個範例中 N 取8)
N=8 weights = np.hanning(N) #呼叫hanning 函數計算權重,生成一個長度為8的視窗 print("Weights", weights)
執行結果:
Weights [0. 0.1882551 0.61126047 0.95048443 0.95048443 0.61126047 0.1882551 0. ]
2)用 convolve 函數計算closes的股票收益率,以歸一化處理後的 weights 作為引數
closes_returns = np.diff(closes) / closes[ : -1] #計算收盤價相鄰差價
smooth_closes = np.convolve(weights/weights.sum(), closes_returns) [N-1:-N+1]#利用權重,計算資料平滑
opens_returns = np.diff(opens) / opens[ : -1] #計算開盤價相鄰差價
smooth_opens = np.convolve(weights/weights.sum(), opens_returns) [N-1:-N+1]
3)用 Matplotlib 繪圖
t = np.arange(N - 1, len(closes_returns))
plt.plot(t, closes_returns[N-1:], lw=1.0)
plt.plot(t, smooth_closes, lw=2.0)
plt.plot(t, opens_returns[N-1:], lw=1.0)
plt.plot(t, smooth_opens, lw=2.0)
plt.show()
執行結果:
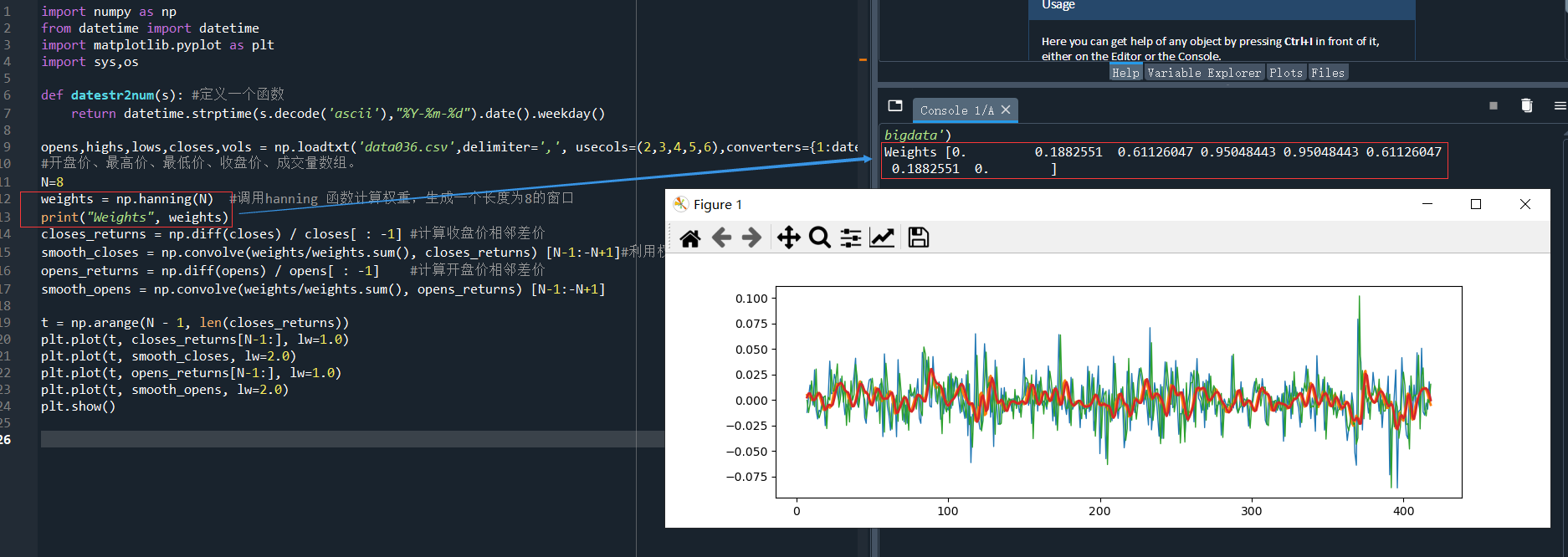
4)
如上圖中的折線有交叉,這些交叉點可能就是股價趨勢的轉折點,至少可以表明closes和opens之間的股價關係發生了變化,這些轉折點可能會經常出現,可以利用它們預測未來的股價走勢。
使用多項式擬合平滑後兩組資料,解出的兩個多項式取值相等時(即在哪些地方存在交叉點),這等價於先對兩個多項式函數作差,然後對所得的多項式函數求根。使用 polysub 函數對多項式作差如下:
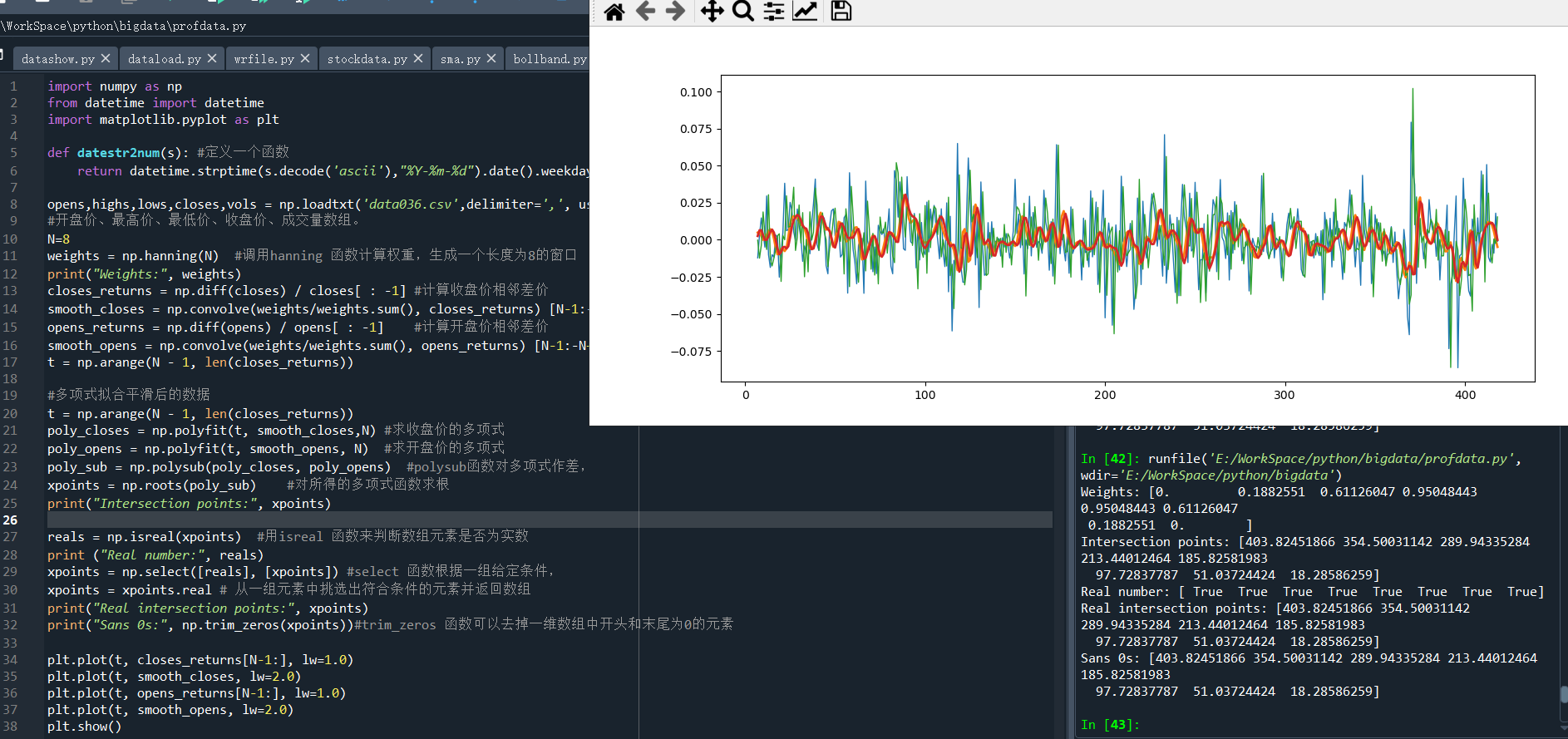
t = np.arange(N - 1, len(closes_returns)) poly_closes = np.polyfit(t, smooth_closes,N) #求收盤價的多項式 poly_opens = np.polyfit(t, smooth_opens, N) #求收盤價的多項式 poly_sub = np.polysub(poly_closes, poly_opens) #polysub函數對多項式作差, xpoints = np.roots(poly_sub) #對所得的多項式函數求根 print("Intersection points:", xpoints)
執行結果:
Intersection points: [403.82451866 354.50031142 289.94335284 213.44012464 185.82581983 97.72837787 51.03724424 18.28586259]
5)用 isreal 函數來判斷陣列元素是否為實數,用 select 函數選出它們。 select 函數可根據一組給定的條件,從一組元素中挑選出符合條件的元素並返回陣列。
得到的實數交叉點、再去掉其中為0的元素。 trim_zeros 函數可以去掉一維陣列中開頭和末尾為0的元素。
reals = np.isreal(xpoints) #用isreal 函數來判斷陣列元素是否為實數 print ("Real number:", reals) xpoints = np.select([reals], [xpoints]) #select 函數根據一組給定條件, xpoints = xpoints.real # 從一組元素中挑選出符合條件的元素並返回陣列 print("Real intersection points:", xpoints) print("Sans 0s:", np.trim_zeros(xpoints))#trim_zeros 函數可以去掉一維陣列中開頭和末尾為0的元素
執行結果如下:
Intersection points: [403.82451866 354.50031142 289.94335284 213.44012464 185.82581983 97.72837787 51.03724424 18.28586259] Real number: [ True True True True True True True True] Real intersection points: [403.82451866 354.50031142 289.94335284 213.44012464 185.82581983 97.72837787 51.03724424 18.28586259] Sans 0s: [403.82451866 354.50031142 289.94335284 213.44012464 185.82581983 97.72837787 51.03724424 18.28586259]
完整程式碼如下:
import numpy as np from datetime import datetime import matplotlib.pyplot as plt def datestr2num(s): #定義一個函數 return datetime.strptime(s.decode('ascii'),"%Y-%m-%d").date().weekday() opens,highs,lows,closes,vols = np.loadtxt('data036.csv',delimiter=',', usecols=(2,3,4,5,6),converters={1:datestr2num},unpack=True) #開盤價、最高價、最低價、收盤價、成交量陣列。 N=8 weights = np.hanning(N) #呼叫hanning 函數計算權重,生成一個長度為8的視窗 print("Weights:", weights) closes_returns = np.diff(closes) / closes[ : -1] #計算收盤價相鄰差價 smooth_closes = np.convolve(weights/weights.sum(), closes_returns) [N-1:-N+1]#利用權重,計算資料平滑 opens_returns = np.diff(opens) / opens[ : -1] #計算開盤價相鄰差價 smooth_opens = np.convolve(weights/weights.sum(), opens_returns) [N-1:-N+1] t = np.arange(N - 1, len(closes_returns)) #多項式擬合平滑後的資料 t = np.arange(N - 1, len(closes_returns)) poly_closes = np.polyfit(t, smooth_closes,N) #求收盤價的多項式 poly_opens = np.polyfit(t, smooth_opens, N) #求收盤價的多項式 poly_sub = np.polysub(poly_closes, poly_opens) #polysub函數對多項式作差, xpoints = np.roots(poly_sub) #對所得的多項式函數求根 print("Intersection points:", xpoints) reals = np.isreal(xpoints) #用isreal 函數來判斷陣列元素是否為實數 print ("Real number:", reals) xpoints = np.select([reals], [xpoints]) #select 函數根據一組給定條件, xpoints = xpoints.real # 從一組元素中挑選出符合條件的元素並返回陣列 print("Real intersection points:", xpoints) print("Sans 0s:", np.trim_zeros(xpoints))#trim_zeros 函數可以去掉一維陣列中開頭和末尾為0的元素 plt.plot(t, closes_returns[N-1:], lw=1.0) plt.plot(t, smooth_closes, lw=2.0) plt.plot(t, opens_returns[N-1:], lw=1.0) plt.plot(t, smooth_opens, lw=2.0) plt.show()