論文資訊

論文標題：Learning Graph Embedding with Adversarial Training Methods
論文作者：Shirui Pan, Ruiqi Hu, Sai-fu Fung, Guodong Long, Jing Jiang, Chengqi Zhang
論文來源：2020, ICLR
論文地址：download 
論文程式碼：download

1 Introduction

　　眾多圖嵌入方法關注於儲存圖結構或最小化重構損失，忽略了隱表示的嵌入分佈形式，因此本文提出對抗正則化框架（adversarially regularized framework）。

2 Method

　　ARGA 框架如下：

　　

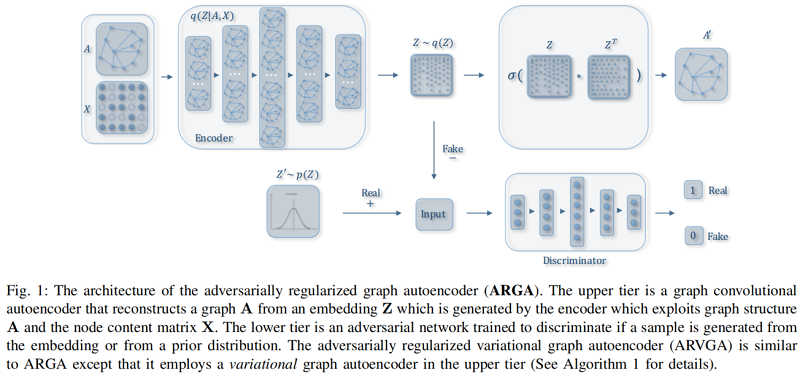
　　組成部分：

• • Graph convolutional autoencoder
  • Adversarial regularization

2.1 Graph Convolutional Autoencoder

　　一個頻譜折積函數 $f\left(\mathbf{Z}^{(l)}, \mathbf{A} \mid \mathbf{W}^{(l)}\right)$ :

　　　　$\mathbf{Z}^{(l+1)}=f\left(\mathbf{Z}^{(l)}, \mathbf{A} \mid \mathbf{W}^{(l)}\right)  \quad\quad\quad(1)$

　　採用GCN :

　　　　$f\left(\mathbf{Z}^{(l)}, \mathbf{A} \mid \mathbf{W}^{(l)}\right)=\phi\left(\widetilde{\mathbf{D}}^{-\frac{1}{2}} \widetilde{\mathbf{A}} \widetilde{\mathbf{D}}^{-\frac{1}{2}} \mathbf{Z}^{(l)} \mathbf{W}^{(l)}\right) \quad\quad\quad(2)$

　　圖編碼器

　　　　$\mathbf{Z}^{(1)}=f_{\text {Relu }}\left(\mathbf{X}, \mathbf{A} \mid \mathbf{W}^{(0)}\right)  \quad\quad\quad(3)$
　　　　$\mathbf{Z}^{(2)}=f_{\text {linear }}\left(\mathbf{Z}^{(1)}, \mathbf{A} \mid \mathbf{W}^{(1)}\right) \quad\quad\quad(4)$

　　我們的圖折積編碼器 $\mathcal{G}(\mathbf{Z}, \mathbf{A})=   q(\mathbf{Z} \mid \mathbf{X}, \mathbf{A}) $ 將圖結構和節點內容編碼為一個表示的 $\mathbf{Z}=q(\mathbf{Z} \mid \mathbf{X}, \mathbf{A})=\mathbf{Z}^{(2)}$。

　　　　$q\left(\mathbf{z}_{\mathbf{i}} \mid \mathbf{X}, \mathbf{A}\right)=\mathcal{N}\left(\mathbf{z}_{i} \mid \boldsymbol{\mu}_{i}, \operatorname{diag}\left(\boldsymbol{\sigma}^{2}\right)\right)\quad\quad\quad(6)$

　　這裡，$\boldsymbol{\mu}=\mathbf{Z}^{(2)}$ 是均值向量 $\boldsymbol{z}_{i}$ 的矩陣；同樣，$\log \sigma=f_{\text {linear }}\left(\mathbf{Z}^{(1)}, \mathbf{A} \mid \mathbf{W}^{\prime(1)}\right) $ 在 $\text{Eq.3}$ 的第一層與 $\boldsymbol{\mu}$ 共用權值 $\mathbf{W}^{(0)}$。

Decoder model

　　我們的解碼器模型用於重建圖形資料。我們可以重建圖結構 $\mathbf{A}$，內容資訊 $\mathbf{X}$，或者兩者都可以重建，本文注重重建圖結構 $\mathbf{A}$。

　　Decoder 是 $p(\hat{\mathbf{A}} \mid \mathbf{Z})$。

　　我們訓練了一個基於圖嵌入的連結預測層：

　　　　$p(\hat{\mathbf{A}} \mid \mathbf{Z})=\prod_{i=1}^{n} \prod_{j=1}^{n} p\left(\hat{\mathbf{A}}_{i j} \mid \mathbf{z}_{i}, \mathbf{z}_{j}\right)\quad\quad\quad(7)$

　　　　$p\left(\hat{\mathbf{A}}_{i j}=1 \mid \mathbf{z}_{i}, \mathbf{z}_{j}\right)=\operatorname{sigmoid}\left(\mathbf{z}_{i}^{\top}, \mathbf{z}_{j}\right)\quad\quad\quad(8)$

　　這裡的預測 $\hat{\mathbf{A}}$ 應該接近於地面真相 $\mathbf{A}$。

　　嵌入 $Z$ 和重構圖 $\hat{\mathbf{A}}$ 可以表示如下：

　　　　$\hat{\mathbf{A}}=\operatorname{sigmoid}\left(\mathbf{Z} \mathbf{Z}^{\top}\right), \text { here } \mathbf{Z}=q(\mathbf{Z} \mid \mathbf{X}, \mathbf{A})\quad\quad\quad(9)$

Optimization

　　對於圖編碼器，我們通過以下方法來最小化圖資料的重構誤差：

　　　　$\mathcal{L}_{0}=\mathbb{E}_{q(\mathbf{Z} \mid(\mathbf{X}, \mathbf{A}))}[\log p(\mathbf{A} \mid \mathbf{Z})]\quad\quad\quad(10)$

　　對於變分圖編碼器，我們對變分下界進行了優化如下：

　　　　$\mathcal{L}_{1}=\mathbb{E}_{q(\mathbf{Z} \mid(\mathbf{X}, \mathbf{A}))}[\log p(\mathbf{A} \mid \mathbf{Z})]-\mathbf{K L}[q(\mathbf{Z} \mid \mathbf{X}, \mathbf{A}) \| p(\mathbf{Z})]\quad\quad\quad(11)$

　　其中，$\mathbf{K L}[q(\bullet) \| p(\bullet)]$ 是 $q(\bullet)$ 和 $p(\bullet)$ 之間的 KL 散度。$p(\bullet)$ 是一個先驗分佈，它在實踐中可以是一個均勻分佈，也可以是一個高斯分佈 ：$p(\mathbf{Z})= \prod\limits_{i} p\left(\mathbf{z}_{i}\right)=\prod\limits_{i} \mathcal{N}\left(\mathbf{z}_{i} \mid 0, \mathbf{I}\right)$。

2.2  Adversarial Model $\mathcal{D}(\mathbf{Z}) $

　　我們的模型的基本思想是強制潛在表示 $\mathbf{Z}$ 來匹配一個先驗分佈，這是通過一個對抗性的訓練模型來實現的。對抗性模型是建立在一個標準的多層感知器(MLP)上，其中輸出層只有一維的 $sigmoid$ 函數。對抗模型作為一個鑑別器來區分潛在程式碼是來自先前的 $p_{z}$（positive）還是圖編碼器 $\mathcal{G}(\mathbf{X}, \mathbf{A})$（negative）。通過最小化訓練二值分類器的交叉熵代價，最終在訓練過程中對嵌入方法進行正則化和改進。該成本的計算方法如下：

　　　　$-\frac{1}{2} \mathbb{E}_{\mathbf{z} \sim p_{z}} \log \mathcal{D}(\mathbf{Z})-\frac{1}{2} \mathbb{E}_{\mathbf{X}} \log (1-\mathcal{D}(\mathcal{G}(\mathbf{X}, \mathbf{A}))) \quad\quad\quad(12)$

　　在我們的論文中，我們檢查了對所有模型和任務，設定 $p_{z}$ 為高斯分佈和均勻分佈。

Adversarial Graph Autoencoder Model

　　用鑑別器 $\mathcal{D}(\mathbf{Z})$ 訓練編碼器模型的方程可以寫如下：

　　　　$\underset{\mathcal{G}}{\text{min }}  \underset{\mathcal{D}}{\text{max }} \mathbb{E}_{\mathbf{z} \sim p_{z}}[\log \mathcal{D}(\mathbf{Z})]+\mathbb{E}_{\mathbf{x} \sim p(\mathbf{x})}[\log (1-\mathcal{D}(\mathcal{G}(\mathbf{X}, \mathbf{A})))]\quad\quad\quad(13)$

　　其中 $\mathcal{G}(\mathbf{X}, \mathbf{A})$ 和 $\mathcal{D}(\mathbf{Z})$ 表示上述說明的發生器和鑑別器。

2.3 Algorithm Explanation

　　演演算法如下：

　　

2.4 Decoder Variations

GCN Decoder for Graph Structure Reconstruction (ARGA GD)

　　這種方法的變體被命名為 ARGAGD。Fig 2 展示了 ARGAGD 的體系結構。

　　

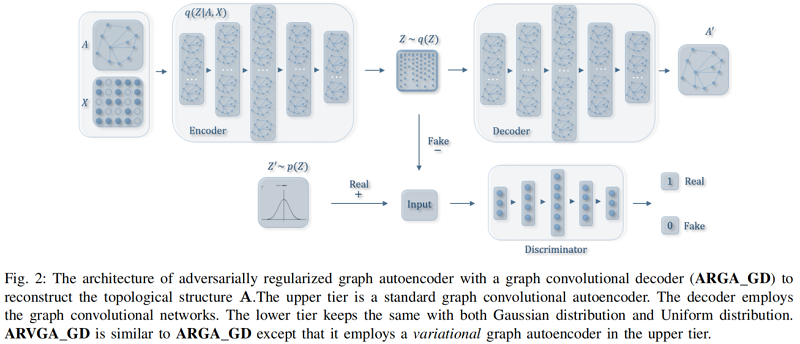
　　在這種方法中，解碼器的輸入將從編碼器中嵌入，並且圖折積解碼器構造如下：

　　　　$\mathbf{Z}_{D}=f_{\text {linear }}\left(\mathbf{Z}, \mathbf{A} \mid \mathbf{W}_{D}^{(1)}\right)\quad\quad\quad(14)$

　　　　$\mathbf{O}=f_{\text {linear }}\left(\mathbf{Z}_{D}, \mathbf{A} \mid \mathbf{W}_{D}^{(2)}\right)\quad\quad\quad(15)$

　　其中，$\mathbf{Z}$ 是從圖編碼器學習到的嵌入，而 $\mathbf{Z}_{D}$ 和 $\mathbf{O}$ 是從圖解碼器的第一層和第二層的輸出。$\mathbf{O}$ 的水平維數等於節點數。然後，我們計算出重建誤差如下：

　　　　$\mathcal{L}_{A R G A_{-} G D}=\mathbb{E}_{q(\mathbf{O} \mid(\mathbf{X}, \mathbf{A}))}[\log p(\mathbf{A} \mid \mathbf{O})]\quad\quad\quad(16)$

GCN Decoder for both Graph Structure and Content Information Reconstruction (ARGA AX)

　　我們進一步修改了我們的圖的折積解碼器，以重建圖的結構 $\mathbf{A}$ 和內容資訊 $\mathbf{X}$。該體系結構如 Fig.3 所示。

　　

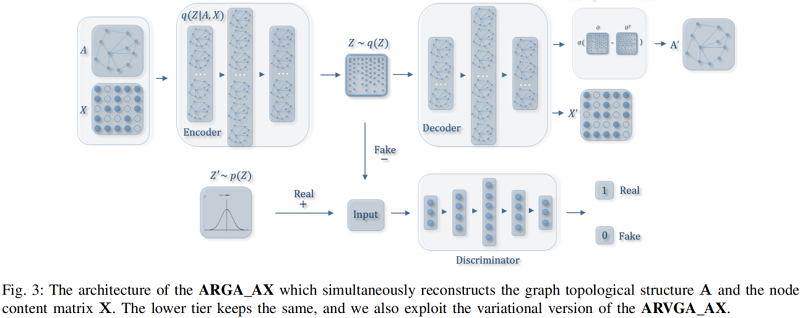
　　我們用與每個節點相關的特徵數固定第二圖折積層的維數，因此第二層的輸出 $\mathbf{O} \in \mathbb{R}^{n \times f} \ni \mathbf{X}$。在這種情況下，重構損失由兩個誤差組成。首先，圖結構的重構誤差可以最小化如下：

　　　　$\mathcal{L}_{A}=\mathbb{E}_{q(\mathbf{O} \mid(\mathbf{X}, \mathbf{A}))}[\log p(\mathbf{A} \mid \mathbf{O})] \quad\quad\quad(17)$

　　然後用類似的公式可以最小化節點內容的重構誤差：

　　　　$\mathcal{L}_{X}=\mathbb{E}_{q(\mathbf{O} \mid(\mathbf{X}, \mathbf{A}))}[\log p(\mathbf{X} \mid \mathbf{O})] \quad\quad\quad(18)$

　　最終的重構誤差是圖的結構和節點內容的重構誤差之和：

　　　　$\mathcal{L}_{0}=\mathcal{L}_{A}+\mathcal{L}_{X}\quad\quad\quad(19)$

3 Experiments

資料集

　　

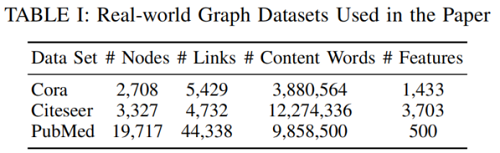
節點聚類

　　

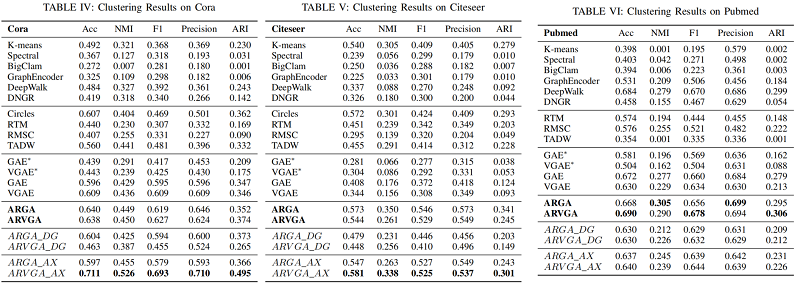
4 Conclusion

　　本文提出了一種新的對抗性圖嵌入框架。我們認為現有的圖嵌入演演算法都是非正則化方法，忽略了潛在表示的資料分佈，在真實圖資料中嵌入不足。我們提出了一種對抗性訓練方案來正則化潛在碼，並強制使潛在碼匹配先驗分佈。對抗性模組與一個圖折積自動編碼器共同學習，以產生一個魯棒表示。我們還利用了ARGA的一些有趣的變化，如ARGADG和ARGAAX，來討論圖折積解碼器對重構圖結構和節點內容的影響。實驗結果表明，我們的演演算法ARGA和ARVGA在鏈路預測和節點聚類任務中優於基線演演算法。

　　反向正則化圖自動編碼器(ARGA)有幾個方向。我們將研究如何使用ARGA模型生成一些真實的圖[64]，這可能有助於發現生物領域的新葯。我們還將研究如何將標籤資訊合併到ARGA中來學習魯棒圖嵌入。