關於區間操作查詢（字首和與差分）+樹狀陣列基礎

今天學了字首和和差分，為了避免我把它忘掉，我還是淺淺的記錄一下吧

首先需要知道什麼是字首和與差分：

字首和就是陣列中某元素之前（包括此元素）的所有元素的和

設b[]為字首和陣列，a[]是原陣列。

對於一維陣列而言，某個元素的字首和就是從這個陣列的第0個元素到這個元素的所有元素之和。

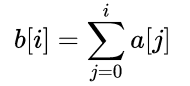
即：

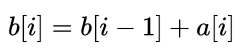
那麼就可以對區間求和產生更深刻的理解：

對於求出一個區間[l,r]的所有元素之和，我們就可以將首元素的字首和與末元素的字首合相減。

程式碼如下：

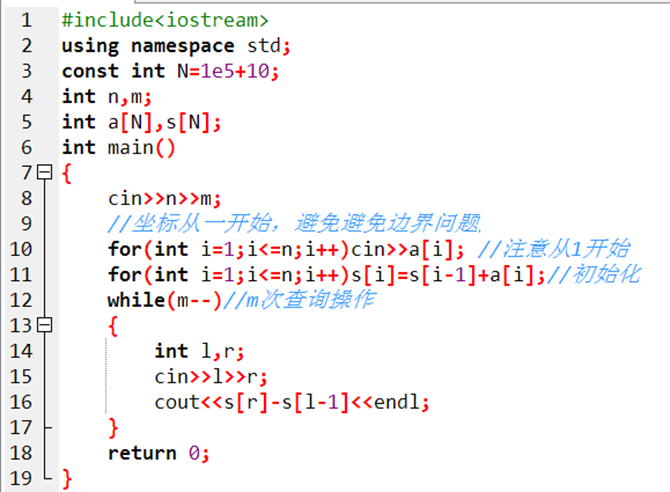
而對於二維陣列來說，每個元素的字首和b[x][y]就是從a[0][0]到a[x][y]之間所有元素的和

比如b[3][1]，就可以如下圖的方法表示：

而如果我想給一個區間求和，就直接表示為：

即：

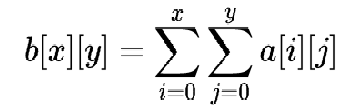
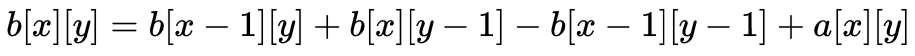
那我要是想給一個區間求和，就可以表示為：

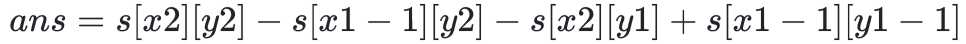
程式碼如下：

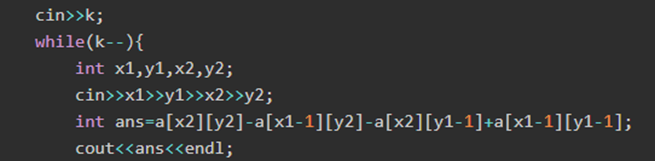
關於差分，就是將當前元素與前一個元素相減。

比如給定一個陣列a[n]={1,3,7,5,2}，他的差分陣列就是d[n]={1,2,4,-2,-3}

他的應用有很多，比如：給定一個序列，m次存取，每次輸入兩個一維坐x1,x2，並輸入一個數c,代表這個數列從第x1個數到第x2個數之間的元素都加c，最後輸出最新的序列。

對於這種題，先求出這個序列的差分陣列d，每次詢問讓[L,R]+V轉化為d[L]+V,d[R+1]-V ，最後再將新陣列求一次字首和即可。

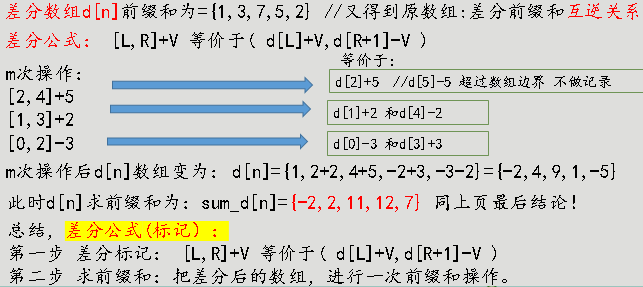
對於二維差分

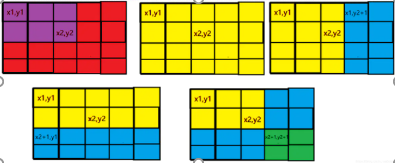
現在我要在左上角是 (x1,y1)，右下角是 (x2,y2) 的矩形區間每個值都 +p

那如果開始位置+p，那根據字首和的性質，那麼它影響的就是整個黃色部分(所有的求和都增加了)，多影響了兩個藍色部分。所以在兩個藍色部分 -p 消除 +p 的影響，而兩個藍色部分重疊的綠色部分多了個 -p 的影響，所以綠色部分 +p 消除影響

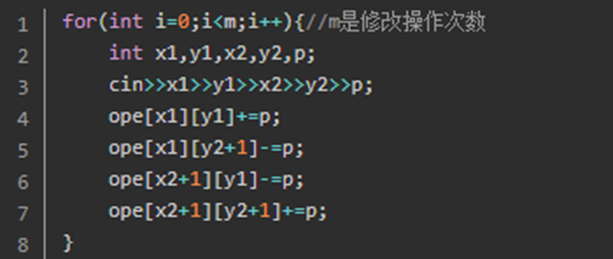
程式碼如下：

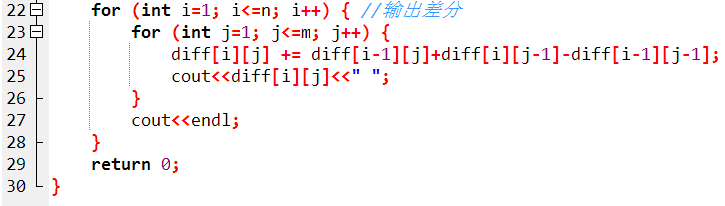
關於lowbit()函數

lowbit(x)是x的二進位制表示式中最低位的1所對應的值

比如12的二進位制可以表示為1100，所以他的lowbit就是1*8等於8

關於他的程式碼實現也很簡單

1 int lowbit(int x)
2 {
3     return x&(-x);
4     //實際上就是負數的二補數運用 
5 }

如何用lowbit()來維護其區間

設結點的編號為x，那麼這個結點維護的區間就是 (x-lowbit(x),x] (注意區間的開閉）

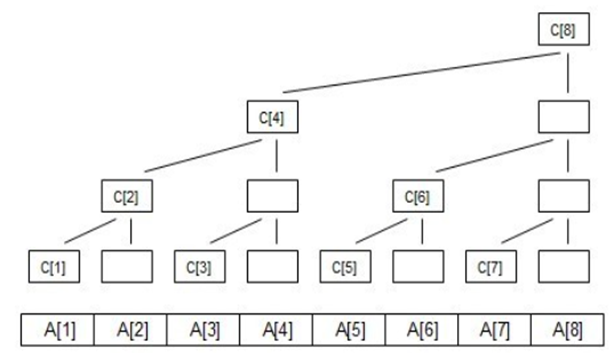
c₁維護區間(1-lowbit(1)，1]即(0,1] 也就是A₁本身

c₂維護區間(2-lowbit(2)，2]即(0,2] A₁+A₂

c₃維護(2,3] A₃

c₄維護(0,4] A₁+A₂+A₃+A₄

c₅維護(4,5] A₅

c₆維護(4,6] A₅+A₆

c₇維護(6,7] A₇

c₈維護(0,8] A₁+A₂+A₃+A₄+A₅+A₆+A₇+A₈

不難發現，結點維護的葉結點（A單點區間）的個數就是其序號轉換為二進位制後lowbit的值

通過尋找規律，可以得到通式：

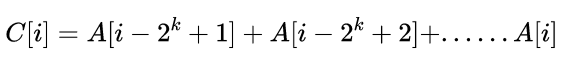
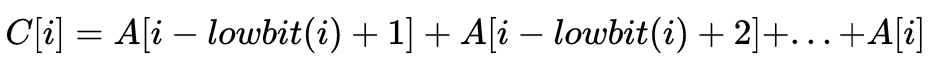
尋找樹狀陣列的性質：

(性質1)每個內部結點C[x]儲存以它為根的子樹中所有葉結點的和。

(性質2)每個內部結點C[x]的子結點個數等於lowbit(x)的值。

(性質3)除樹根以外，每個內部結點C[x]的父親結點是C[x+lowbit(x)]

(性質4)樹的深度為O(logN)

通過這些性質，我們可以進行一系列操作：

1、查詢字首和：

 1 int lowbit(x)
 2 {
 3     return x&(-x);
 4 }
 5 
 6 int sum(int x)//查詢字首和（c[x]的區間和） 
 7 {
 8     int res=0;
 9     while(x>0)
10     {
11         res=res+c[x];
12         x=x-lowbit(x);
13     }
14     return res;
15 }

2.單點修改：

 1 int lowbit(int x) 
 2 {
 3     return x&(-x);
 4 }
 5 void update(int x,int y)
 6 //a[x]+y操作，並讓他的長輩加y 
 7 {
 8     while(x<=n)
 9     {
10         c[x]+=y;
11         x+=lowbit(x);
12     }
13 }

3、區間和計算

int calculate(int x,int y)
{
    return sum(y)-sum(x-1);
}

經典題目：

 1 #include<cstdio>
 2 #include<iostream>
 3 using namespace std;
 4 int c[100001];
 5 int n,m,k,a,b;
 6 int lowbit(int x)
 7 {
 8     return x&(-x);
 9 }
10 
11 void update(int x,int v)
12 //單點修改（在x的位置上加v） 
13 {
14     while(x<=n)
15     {
16         c[x]+=v;
17         x+=lowbit(x);
18     }
19 }
20 
21 int sum(int x)
22 {
23     int res=0;
24     while(x>0)
25     {
26         res+=c[x];
27         x-=lowbit(x);
28     }
29     return res;
30 }
31 
32 int main()
33 {
34     int v;
35     scanf("%d%d",&n,&m);
36     for(int i=1;i<=n;i++)
37     {
38         scanf("%d",&v);
39         update(i,v);
40     } 
41     for(int i=1;i<=m;i++)
42     {
43         scanf("%d%d%d",&k,&a,&b);
44         if(k==0) printf("%d\n",sum(b)-sum(a-1));
45         else update(a,b);
46     }
47     return 0;
48 }

就先到這裡吧，再見！