畢設(5)—笛卡爾空間軌跡規劃(直線、圓弧)
2022-06-05 18:01:21
畢設中用到了很多程式碼,其中一部分我通過看書和看論文學習並實現的程式碼,會通過Gitee倉庫分享出來,這些程式碼僅用於學習使用,祝各位畢業生順利完成畢設!
畢設系列內容:畢業設計——四自由度機械臂軌跡規劃
畢設(5)—笛卡爾空間軌跡規劃(直線、圓弧)
機械臂在笛卡爾空間中常用的規劃演演算法有直線和圓弧兩種,他們的具體實現都是通過運動學逆解將運動軌跡轉化為關節角度變化序列的方式。
直線軌跡規劃
設機械臂任務是從空間中兩點\(P_1\)、\(P_2\)間運動,如下圖所示
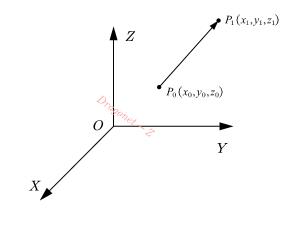
則兩點長度\(L\)可得
\[L=\sqrt{(x_1-x_0)^2+(y_1-y_0)^2+(z_1-z_0)^2}
\]
在本文中採用的速度規劃是勻速,如果有S型之類的速度規劃演演算法也可以採用
\[d=v\cdot t
\]
d為一個插補週期內移動的距離,t為插補的時間間隔
圓弧軌跡規劃
空間中兩兩不在同一條直線的三點可確定一個平面,也可以確定一個圓弧。設空間中有三點\(P_1\)、\(P_2\)、\(P_3\),機械臂需要通過三點沿圓弧軌跡運動,如下圖所示
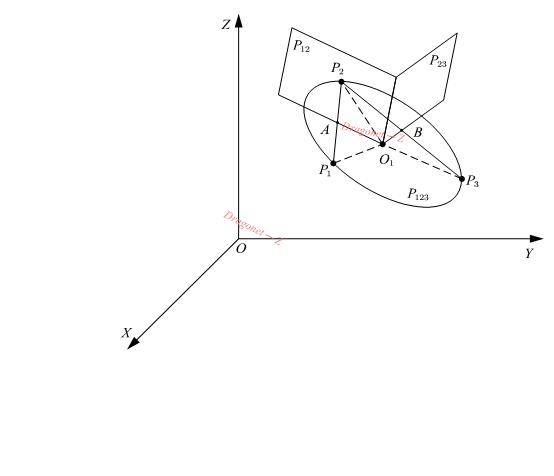
向量圖我用的是AxGlyph軟體畫的,有需要可以自行到官網購買
公式太多,不再贅述,大致流程如下
- 求出\(P_{123}\)、\(P_{12}\)和\(P_{23}\)的方程,通過三個平面方程獲得圓心\(O_1\)座標和圓弧半徑
- 在\(P_{123}\)平面建立新座標系,計算兩個座標系之間的齊次變換矩陣
- 在\(P_{123}\)平面計算平面圓弧的軌跡,通過變換矩陣轉換為空間圓弧軌跡
- 圓弧軌跡通過運動學逆解轉換為各關節角度變化序列
Matlab程式碼驗證
程式碼有點長,具體函數程式碼可以到倉庫中自行查詢
test4.m
clear, clc, close all;
L(1) = Link([0 0 0 0 0 0], 'modified');
L(2) = Link([0 0 0 -pi / 2 0 0], 'modified');
L(3) = Link([0 0 135 0 0 0], 'modified');
L(4) = Link([0 0 147 0 0 0], 'modified');
L(5) = Link([0 131 61 -pi / 2 0 0], 'modified');
robot = SerialLink(L, 'name', 'Dobot');
angle1 = [-pi / 3, -pi / 9, pi / 3, -2 * pi / 9, 0];
angle2 = [-pi / 9, -pi / 3, pi / 2, -pi / 6, pi / 9];
angle3 = [7 * pi / 36, -pi / 4, 5 * pi / 12, -pi / 6, 2 * pi / 9];
angle4 = [4 * pi / 9, -pi / 9, 7 * pi / 18, -5 * pi / 18, pi / 3];
angleT = [angle1; angle2; angle3];
for i = 1:size(angleT, 1)
fk = myfkine(angleT(i, :));
points(i, :) = [fk(1, 4), fk(2, 4), fk(3, 4)];
theta5(i) = angleT(i, 5);
end
[q, t] = line_traj(points, theta5, [0, 5], 100);
%[q, t] = arc_traj(points, theta5, [0, 5, 10], 40);
qdeg = rad2deg(q);
figure(1);
T = zeros(4, 4, size(q, 1));
for i = 1:size(q, 1)
T(:, :, i) = myfkine(q(i, :));
end
plot3(squeeze(T(1, 4, :)), squeeze(T(2, 4, :)), squeeze(T(3, 4, :)), 'r-', 'LineWidth', 2);
title('軌跡圖');
hold on;
plot3(points(:, 1), points(:, 2), points(:, 3), 'bo', 'MarkerSize', 7, 'LineWidth', 2);
hold on;
robot.plot(q);
grid on;
hold on;
figure(2);
plot(t, qdeg);
title('角度圖');
legend('q_1', 'q_2', 'q_3', 'q_4', 'q_5');
xlabel('t(s)');
ylabel('deg(°)');
grid on;
hold on;
直線規劃執行結果如下
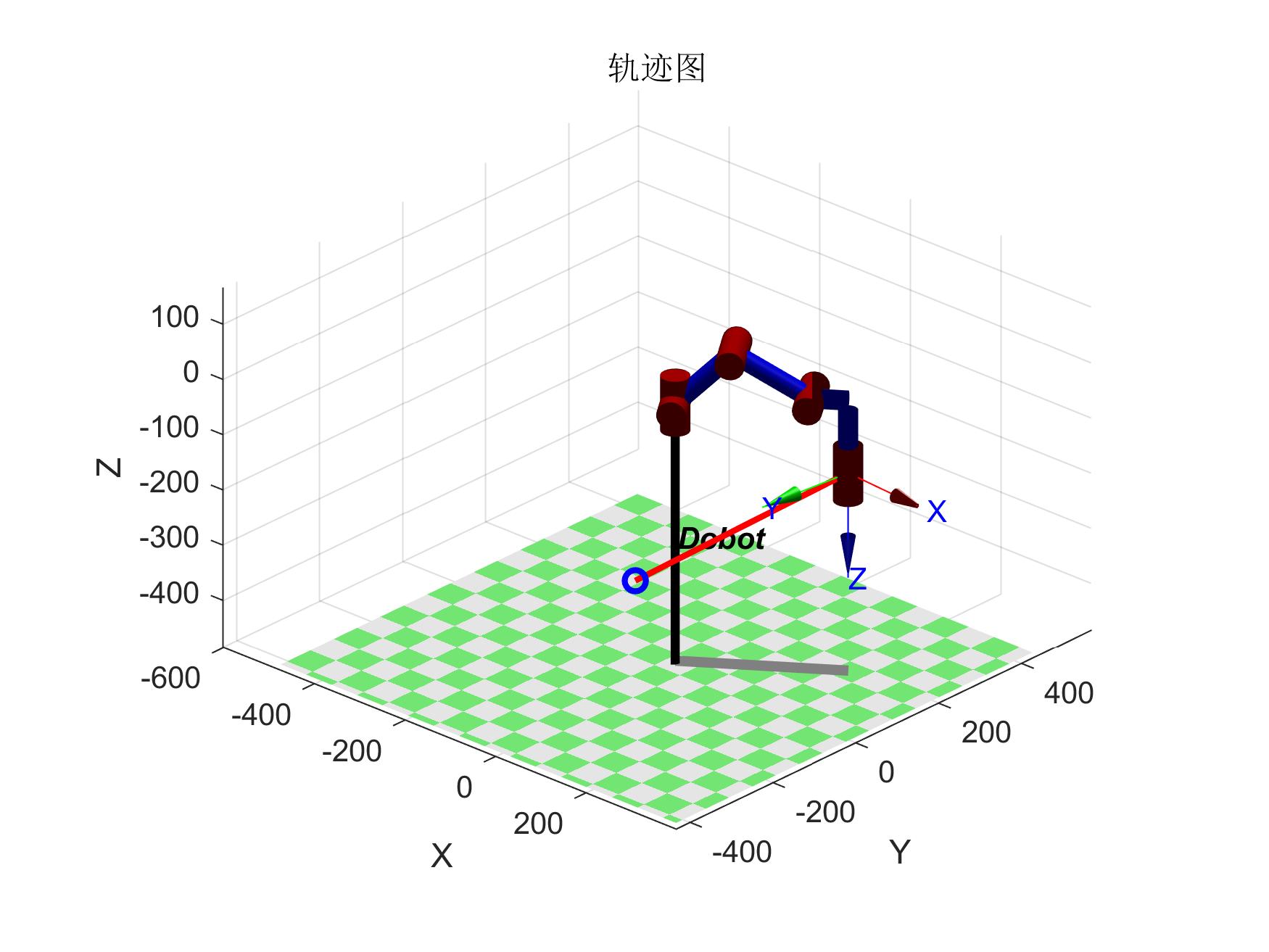 直線軌跡圖 直線軌跡圖 |
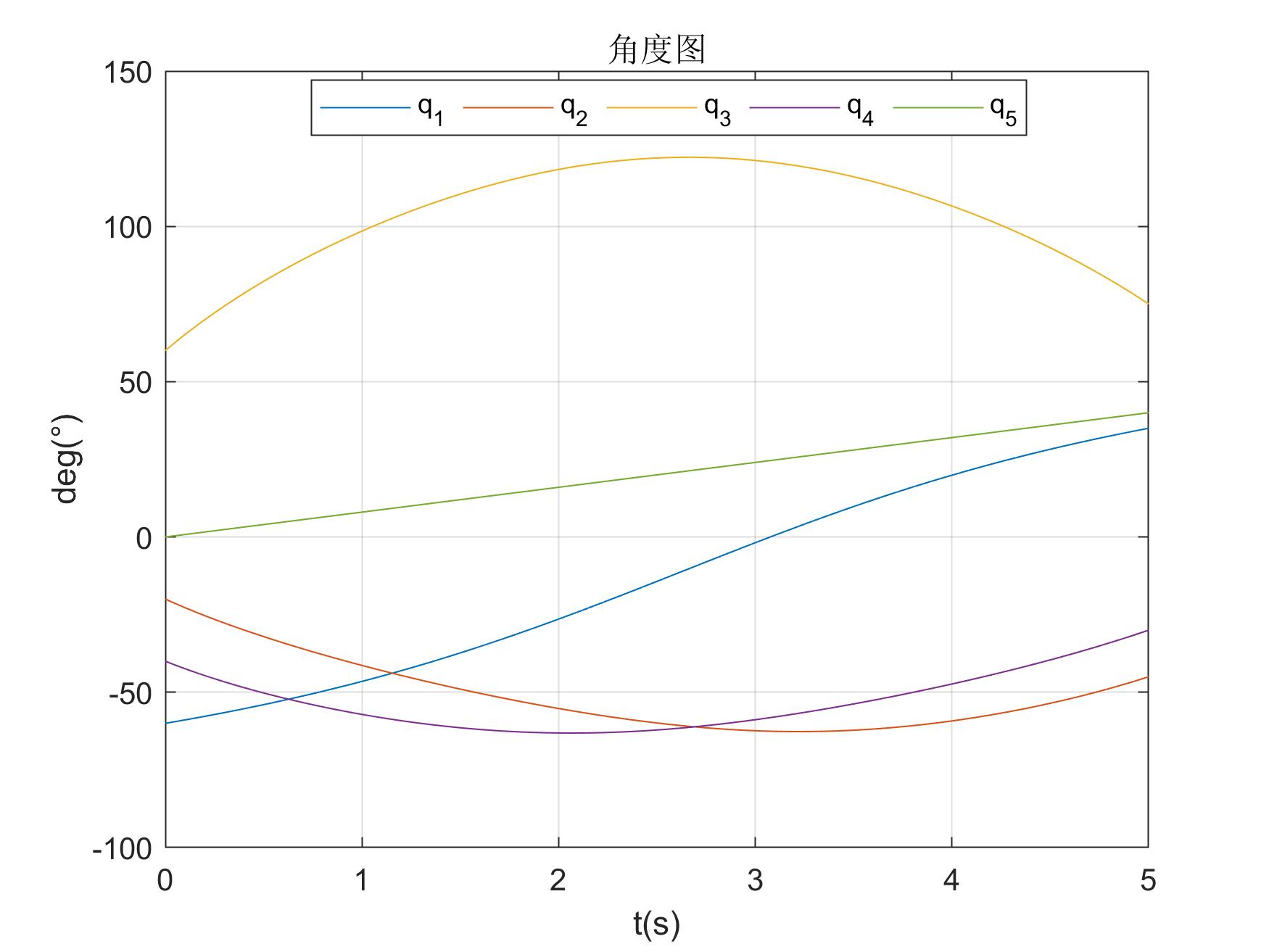 直線角度圖 直線角度圖 |
圓弧規劃執行結果如下
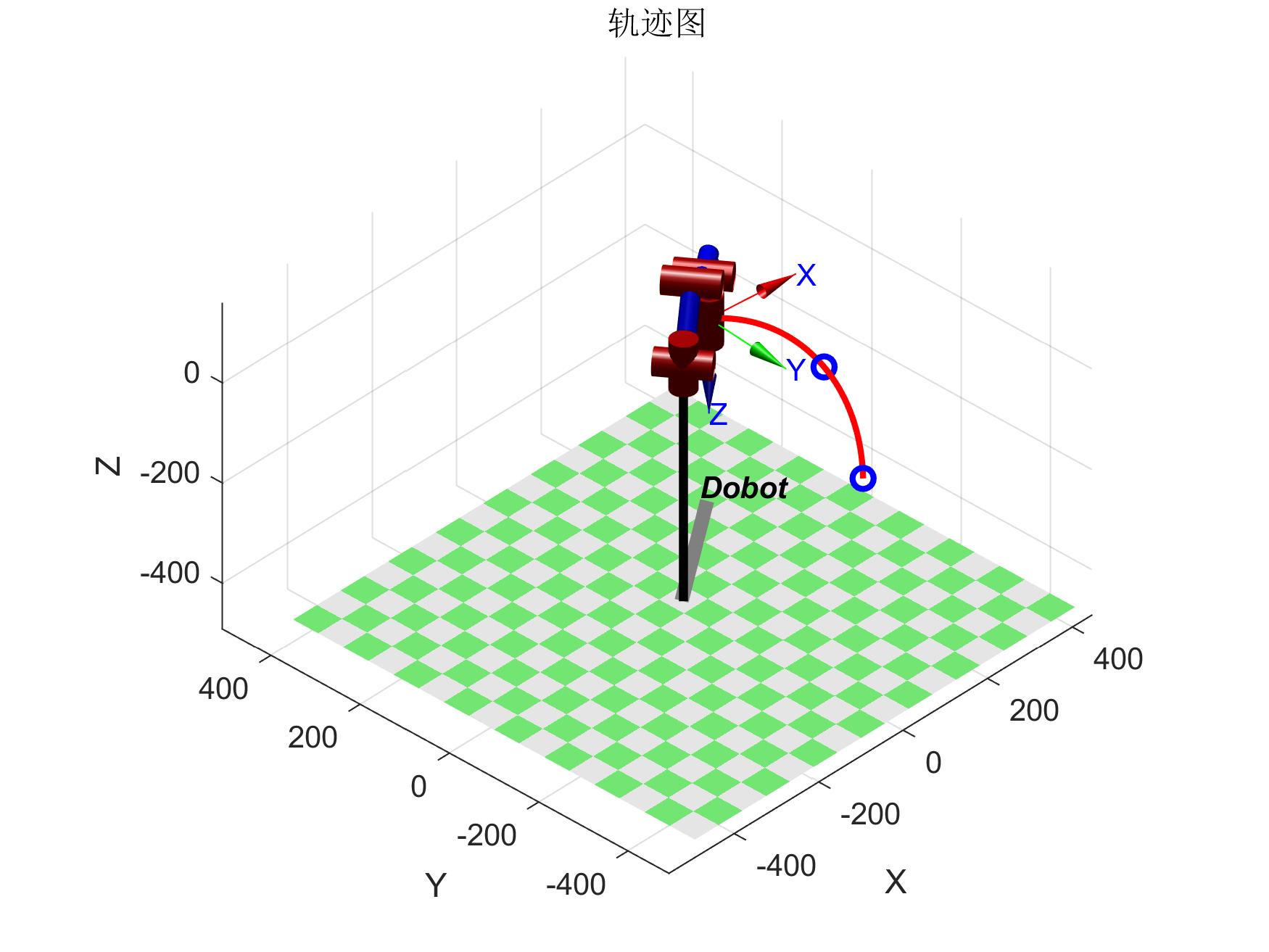 圓弧軌跡圖 圓弧軌跡圖 |
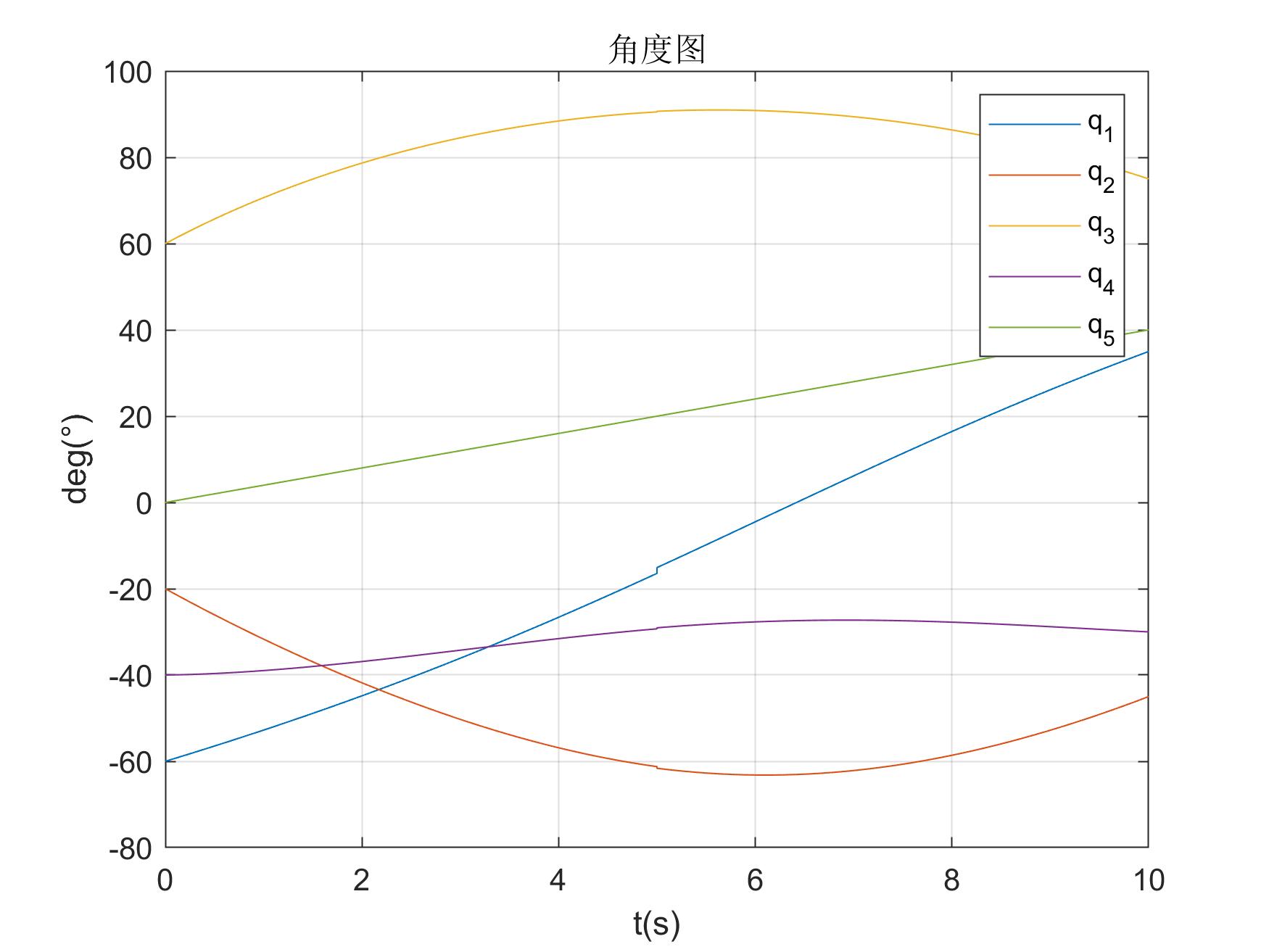 圓弧角度圖 圓弧角度圖 |
可以注意到圓弧角度圖在t=5秒時刻有一次跳變,應該是我重新寫函數的時候漏了一些東西沒寫(pointT向量長度是2step+1,而q向量長度為2step,我重寫函數的時候直接去掉中間的一位pointT了)
for i = 0:theta13 / (2 * step - 1):theta13 %這個地方我直接減1了,原來我寫的函數是沒有這個的
pointT(j, :) = transT * [R * cos(i), R * sin(i), 0, 1]';
j = j + 1;
end
本文到此結束,後續會繼續更新的~