論文解讀(SUBLIME)《Towards Unsupervised Deep Graph Structure Learning》
論文資訊
論文標題:Towards Unsupervised Deep Graph Structure Learning
論文作者:Yixin Liu, Yu Zheng, Daokun Zhang, Hongxu Chen, Hao Peng, Shirui Pan
論文來源:2022, WWW Best Paper Award candidate
論文地址:download
論文程式碼:download
1 Introduction
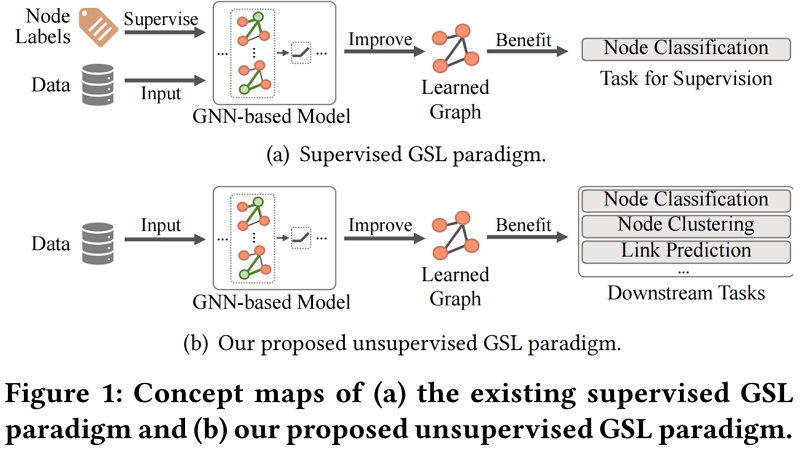
Deep GSL(深度圖結構學習):在節點分類任務的監督下和GNN共同優化圖結構。弊端是對標籤的依賴、邊分佈的偏差、應用程式任務的限制等。
本文和監督 GSL 對比:
2 Problem Definition
符號定義:
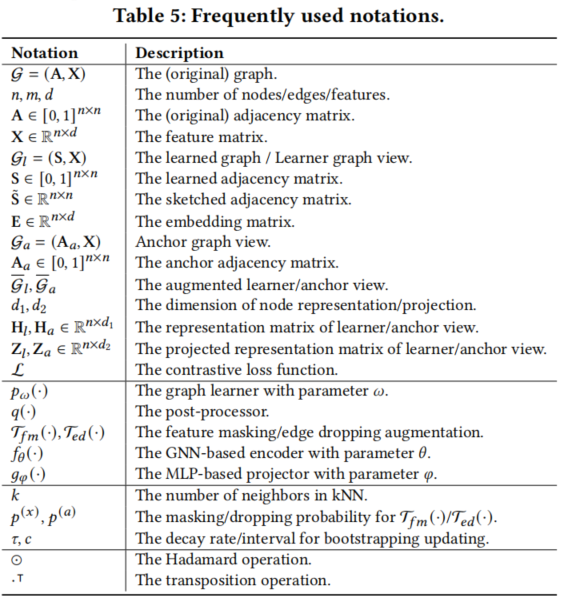
Definition 3.1 (Structure inference). Given a feature matrix $\mathbf{X} \in \mathbb{R}^{n \times d}$ , the target of structure inference is to automatically learn a graph topology $\mathrm{S} \in[0,1]^{n \times n}$ , which reflects the underlying correlations among data samples. In particular, $\mathrm{S}_{i j} \in[0,1]$ indicates whether there is an edge between two samples (nodes) $\mathbf{x}_{i}$ and $\mathbf{x}_{j}$ .
Definition 3.2 (Structure refinement). Given a graph $\mathcal{G}=(\mathbf{A}, \mathbf{X})$ with a noisy graph structure $\mathbf{A}$ , the target of structure refinement is to refine $\mathrm{A}$ to be the optimized adjacency matrix $\mathrm{S} \in[0,1]^{n \times n}$ to better capture the underlying dependency between nodes.
3 Method
整體框架:
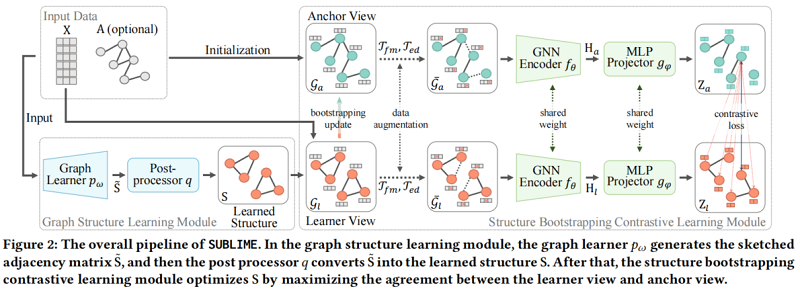
包括兩個模組:
-
- graph structure learning module
- structure bootstrapping contrastive learning module
3.1 Graph Learner
Graph Learner 生成一個帶引數的圖鄰接矩陣 $\tilde{\mathrm{S}} \in \mathbb{R}^{n \times n}$。本文的 Graph Learner 包括如下四種:
-
- FGP learner
- Attentive Learner
- MLP Learner
- GNN Learner
3.1.1 FGP learner
通過一個引數矩陣直接建模鄰接矩陣的每個元素,沒有任何額外的輸入。FGP Learner:
$\tilde{\mathrm{S}}=p_{\omega}^{F G P}=\sigma(\Omega)\quad\quad\quad(1)$
其中,$\omega=\Omega \in \mathbb{R}^{n \times n}$ 是一個引數矩陣,$\sigma(\cdot)$ 是一個非線性函數,使訓練更穩定。FGP學習器背後的假設是,每條邊都獨立地存在於圖中。

class FGP_learner(nn.Module):
def __init__(self, features, k, knn_metric, i, sparse):
super(FGP_learner, self).__init__()
self.k = k
self.knn_metric = knn_metric
self.i = i
self.sparse = sparse
self.Adj = nn.Parameter(
torch.from_numpy(nearest_neighbors_pre_elu(features, self.k, self.knn_metric, self.i)))
def forward(self, h):
if not self.sparse:
Adj = F.elu(self.Adj) + 1
else:
Adj = self.Adj.coalesce()
Adj.values = F.elu(Adj.values()) + 1
return Adj
def nearest_neighbors_pre_elu(X, k, metric, i):
adj = kneighbors_graph(X, k, metric=metric)
adj = np.array(adj.todense(), dtype=np.float32)
adj += np.eye(adj.shape[0])
adj = adj * i - i
return adj
與 FGP Learner 不同,基於度量學習的Learner [7,58] 首先從輸入資料中獲取節點嵌入 $\mathbf{E} \in \mathbb{R}^{n \times d}$,然後利用節點嵌入的兩兩相似性對 $\tilde{\mathrm{S}}$ 進行建模:
$\tilde{\mathrm{S}}=p_{\omega}^{M L}(\mathbf{X}, \mathbf{A})=\phi\left(h_{\omega}(\mathbf{X}, \mathrm{A})\right)=\phi(\mathbf{E})\quad\quad\quad(2)$
其中,$h_{\omega}(\cdot)$ 是一個基於神經網路的帶引數 $\omega$ 的嵌入函數,而且 $\phi(\cdot)$ 是一個非引數度量函數(如餘弦相似度或閔可夫斯基距離),它計算成對相似度。
對於不同的 $h_{\omega}(\cdot)$,本文是 Attentive Learner、MLP Learner、GNN Learner 。
3.1.2 Attentive Learner
採用一個注意網路作為其嵌入網路:
$\mathbf{E}^{(l)}=h_{w}^{(l)}\left(\mathbf{E}^{(l-1)}\right)=\sigma\left(\left[\mathbf{e}_{1}^{(l-1)} \odot \omega^{(l)}, \cdots, \mathbf{e}_{n}^{(l-1)} \odot \omega^{(l)}\right]^{\top}\right)\quad\quad\quad(3)$
其中:
-
- $\mathbf{E}^{(l)}$ 是第 $l$ 層嵌入矩陣,$\mathbf{e}_{i}^{(l-1)} \in \mathbb{R}^{d}$ 是 $\mathbf{E}^{(l-1)}$ 第 $i$ 行向量;
- $\omega^{(l)} \in \mathbb{R}^{d}$ 是第 $l$ 層的引數向量;

class ATT_learner(nn.Module):
def __init__(self, nlayers, isize, k, knn_metric, i, sparse, mlp_act):
super(ATT_learner, self).__init__()
self.i = i
self.layers = nn.ModuleList()
for _ in range(nlayers):
self.layers.append(Attentive(isize))
self.k = k
self.knn_metric = knn_metric
self.non_linearity = 'relu'
self.sparse = sparse
self.mlp_act = mlp_act
def internal_forward(self, h):
for i, layer in enumerate(self.layers):
h = layer(h)
if i != (len(self.layers) - 1):
if self.mlp_act == "relu":
h = F.relu(h)
elif self.mlp_act == "tanh":
h = F.tanh(h)
return h
def forward(self, features):
if self.sparse:
embeddings = self.internal_forward(features)
rows, cols, values = knn_fast(embeddings, self.k, 1000)
rows_ = torch.cat((rows, cols))
cols_ = torch.cat((cols, rows))
values_ = torch.cat((values, values))
values_ = apply_non_linearity(values_, self.non_linearity, self.i)
adj = dgl.graph((rows_, cols_), num_nodes=features.shape[0], device='cuda')
adj.edata['w'] = values_
return adj
else:
embeddings = self.internal_forward(features)
embeddings = F.normalize(embeddings, dim=1, p=2)
similarities = cal_similarity_graph(embeddings)
similarities = top_k(similarities, self.k + 1)
similarities = apply_non_linearity(similarities, self.non_linearity, self.i)
return similarities
class Attentive(nn.Module):
def __init__(self, isize):
super(Attentive, self).__init__()
self.w = nn.Parameter(torch.ones(isize))
def forward(self, x):
return x @ torch.diag(self.w)
3.1.3 MLP Learner
使用多層感知(MLP)作為其嵌入網路:
$\mathbf{E}^{(l)}=h_{w}^{(l)}\left(\mathbf{E}^{(l-1)}\right)=\sigma\left(\mathbf{E}^{(l-1)} \Omega^{(l)}\right)\quad\quad\quad(4)$
其中,$\Omega^{(l)} \in \mathbb{R}^{d \times d}$ 是第 $l$ 層的引數矩陣。
與 Attentive Learner 相比,MLP Learner 進一步考慮了特徵的相關性和組合,為下游相似性度量學習生成了更多的資訊嵌入。

class MLP_learner(nn.Module):
def __init__(self, nlayers, isize, k, knn_metric, i, sparse, act):
super(MLP_learner, self).__init__()
self.layers = nn.ModuleList()
if nlayers == 1:
self.layers.append(nn.Linear(isize, isize))
else:
self.layers.append(nn.Linear(isize, isize))
for _ in range(nlayers - 2):
self.layers.append(nn.Linear(isize, isize))
self.layers.append(nn.Linear(isize, isize))
self.input_dim = isize
self.output_dim = isize
self.k = k
self.knn_metric = knn_metric
self.non_linearity = 'relu'
self.param_init()
self.i = i
self.sparse = sparse
self.act = act
def internal_forward(self, h):
for i, layer in enumerate(self.layers):
h = layer(h)
if i != (len(self.layers) - 1):
if self.act == "relu":
h = F.relu(h)
elif self.act == "tanh":
h = F.tanh(h)
return h
def param_init(self):
for layer in self.layers:
layer.weight = nn.Parameter(torch.eye(self.input_dim))
def forward(self, features):
if self.sparse:
embeddings = self.internal_forward(features)
rows, cols, values = knn_fast(embeddings, self.k, 1000)
rows_ = torch.cat((rows, cols))
cols_ = torch.cat((cols, rows))
values_ = torch.cat((values, values))
values_ = apply_non_linearity(values_, self.non_linearity, self.i)
adj = dgl.graph((rows_, cols_), num_nodes=features.shape[0], device='cuda')
adj.edata['w'] = values_
return adj
else:
embeddings = self.internal_forward(features)
embeddings = F.normalize(embeddings, dim=1, p=2)
similarities = cal_similarity_graph(embeddings)
similarities = top_k(similarities, self.k + 1)
similarities = apply_non_linearity(similarities, self.non_linearity, self.i)
return similarities
3.1.4 GNN Learner
依賴於原始拓撲結構,GNN學習器僅用於結構細化任務(structure refinement task)。
本文采用 GCN 形成嵌入式網路:
$\mathbf{E}^{(l)}=h_{w}^{(l)}\left(\mathbf{E}^{(l-1)}, \mathbf{A}\right)=\sigma\left(\widetilde{\mathbf{D}}^{-\frac{1}{2}} \widetilde{\mathbf{A}} \widetilde{\mathbf{D}}^{-\frac{1}{2}} \mathbf{E}^{(l-1)} \Omega^{(l)}\right)\quad\quad\quad(5)$
其中,$\widetilde{\mathbf{A}}=\mathbf{A}+\mathbf{I}$ 為具有自環的鄰接矩陣,$\widetilde{\mathbf{D}}$ 為 $\tilde{\mathbf{A}}$ 的度矩陣。
GNN學習器假設兩個節點之間的連線不僅與特徵有關,而且還與原始結構有關。

class GNN_learner(nn.Module):
def __init__(self, nlayers, isize, k, knn_metric, i, sparse, mlp_act, adj):
super(GNN_learner, self).__init__()
self.adj = adj
self.layers = nn.ModuleList()
if nlayers == 1:
self.layers.append(GCNConv_dgl(isize, isize))
else:
self.layers.append(GCNConv_dgl(isize, isize))
for _ in range(nlayers - 2):
self.layers.append(GCNConv_dgl(isize, isize))
self.layers.append(GCNConv_dgl(isize, isize))
self.input_dim = isize
self.output_dim = isize
self.k = k
self.knn_metric = knn_metric
self.non_linearity = 'relu'
self.param_init()
self.i = i
self.sparse = sparse
self.mlp_act = mlp_act
def internal_forward(self, h):
for i, layer in enumerate(self.layers):
h = layer(h, self.adj)
if i != (len(self.layers) - 1):
if self.mlp_act == "relu":
h = F.relu(h)
elif self.mlp_act == "tanh":
h = F.tanh(h)
return h
def param_init(self):
for layer in self.layers:
layer.weight = nn.Parameter(torch.eye(self.input_dim))
def forward(self, features):
if self.sparse:
embeddings = self.internal_forward(features)
rows, cols, values = knn_fast(embeddings, self.k, 1000)
rows_ = torch.cat((rows, cols))
cols_ = torch.cat((cols, rows))
values_ = torch.cat((values, values))
values_ = apply_non_linearity(values_, self.non_linearity, self.i)
adj = dgl.graph((rows_, cols_), num_nodes=features.shape[0], device='cuda')
adj.edata['w'] = values_
return adj
else:
embeddings = self.internal_forward(features)
embeddings = F.normalize(embeddings, dim=1, p=2)
similarities = cal_similarity_graph(embeddings)
similarities = top_k(similarities, self.k + 1)
similarities = apply_non_linearity(similarities, self.non_linearity, self.i)
return similarities
3.2 Post-processor
Poster-processor $q(\cdot)$的目標是將鄰接矩陣 $\tilde{S}$ 細化為稀疏、非負、對稱和歸一化鄰接矩陣。
因此,依次採如下步驟:
-
- 稀疏化 $q_{s p}(\cdot)$
- 啟用 $q_{a c t}(\cdot) $
- 對稱 $q_{s y m}(\cdot)$
- 歸一化 $q_{\text {norm }}(\cdot)$
3.2.1 Sparsification
根據相似性建立的鄰接矩陣 $\tilde{\mathrm{S}}$ 通常是密集的,表示一個完全連通的圖結構,但實際上並沒有什麼意義,所以採用基於 K近鄰的稀疏化。
具體地說,對於每個節點,保留具有 $\text{top-k}$ 個連線值的邊,並將其餘的設定為 $0$。稀疏化的 $q_{s p}(\cdot)$ 表示為:
$\tilde{\mathbf{S}}_{i j}^{(s p)}=q_{s p}\left(\tilde{\mathrm{S}}_{i j}\right)=\left\{\begin{array}{ll}\tilde{\mathrm{S}}_{i j}, & \tilde{\mathrm{S}}_{i j} \in \operatorname{top}-\mathrm{k}\left(\tilde{\mathrm{S}}_{i}\right) \\0, & \tilde{\mathrm{S}}_{i j} \notin \operatorname{top}-\mathrm{k}\left(\tilde{\mathrm{S}}_{i}\right)\end{array}\right.\quad\quad\quad(6)$
其中, $top-\mathrm{k}\left(\tilde{\mathrm{S}}_{i}\right)$ 是行向量 $\tilde{\mathrm{S}}_{i}$ 的最大 $k$ 個值的集合。注意,本文並不對 FGP learner 進行稀疏化。
對於大規模圖,使用區域性敏感近似[11] 來執行 kNN 稀疏化,其中最近鄰是從一批節點而不是所有節點中選擇的,這減少了對記憶體的需求。

def cal_similarity_graph(node_embeddings):
similarity_graph = torch.mm(node_embeddings, node_embeddings.t())
return similarity_graph

def top_k(raw_graph, K):
values, indices = raw_graph.topk(k=int(K), dim=-1)
assert torch.max(indices) < raw_graph.shape[1]
mask = torch.zeros(raw_graph.shape).cuda()
mask[torch.arange(raw_graph.shape[0]).view(-1, 1), indices] = 1.
mask.requires_grad = False
sparse_graph = raw_graph * mask
return sparse_graph
3.2.2 Symmetrization and Activation
對稱化和啟用的執行方式為:
$\tilde{\mathbf{S}}^{(s y m)}=q_{s y m}\left(q_{a c t}\left(\tilde{\mathbf{S}}^{(s p)}\right)\right)=\frac{\sigma_{q}\left(\tilde{\mathbf{S}}^{(s p)}\right)+\sigma_{q}\left(\tilde{\mathrm{S}}^{(s p)}\right)^{\top}}{2}\quad\quad\quad(7)$
其中,$\sigma_{q}(\cdot)$ 是一個非線性啟用。對於基於度量學習的學習器,我們將 $\sigma_{q}(\cdot)$ 定義為 ReLU 函數。對於 FGP learner,應用 ELU 函數來防止梯度消失。

def symmetrize(adj): # only for non-sparse
return (adj + adj.T) / 2
3.2.3 Normalization
為了保證邊權值在 $[0,1]$ 範圍內,我們最後對 $\tilde{\mathrm{S}}$ 進行了歸一化。特別地,我們應用了一個對稱的歸一化:
$\mathrm{S}=q_{\text {norm }}\left(\tilde{\mathrm{S}}^{(s y m)}\right)=\left(\tilde{\mathbf{D}}^{(s y m)}\right)^{-\frac{1}{2}} \tilde{\mathbf{S}}^{(s y m)}\left(\tilde{\mathbf{D}}^{(s y m)}\right)^{-\frac{1}{2}}\quad\quad\quad(8)$
其中,$\tilde{\mathbf{D}}^{(s y m)}$ 為 $\tilde{\mathbf{S}}^{(s y m)}$ 的度矩陣。

def normalize(adj, mode, sparse=False):
if not sparse:
if mode == "sym":
inv_sqrt_degree = 1. / (torch.sqrt(adj.sum(dim=1, keepdim=False)) + EOS)
return inv_sqrt_degree[:, None] * adj * inv_sqrt_degree[None, :]
elif mode == "row":
inv_degree = 1. / (adj.sum(dim=1, keepdim=False) + EOS)
return inv_degree[:, None] * adj
else:
exit("wrong norm mode")
else:
adj = adj.coalesce()
if mode == "sym":
inv_sqrt_degree = 1. / (torch.sqrt(torch.sparse.sum(adj, dim=1).values()))
D_value = inv_sqrt_degree[adj.indices()[0]] * inv_sqrt_degree[adj.indices()[1]]
elif mode == "row":
aa = torch.sparse.sum(adj, dim=1)
bb = aa.values()
inv_degree = 1. / (torch.sparse.sum(adj, dim=1).values() + EOS)
D_value = inv_degree[adj.indices()[0]]
else:
exit("wrong norm mode")
new_values = adj.values() * D_value
return torch.sparse.FloatTensor(adj.indices(), new_values, adj.size())
3.3 Multi-view Graph Contrastive Learning
本文使用多檢視對比學習來提供有效的監督訊號來指導圖結構學習。
3.3.1 Graph View Establishment
SUBLIME 將學習到的圖(learner view)定義為一個檢視,並用輸入資料構造另一個檢視(anchor view)。
Learner view
Learner view 採用 $S$ 作為鄰接矩陣,$X$ 作為特徵矩陣,即 $\mathcal{G}_{l}=(\mathrm{S}, \mathrm{X})$。在每次訓練迭代中,$\mathrm{S}$ 和用於建模的引數通過梯度下降直接更新,以發現最優的圖結構。
在 SUBLIME 中,將 learner views 初始化為建立在特徵基礎上的 kNN 圖 [11,12]。具體來說,
- 對於 FGP learner,將 kNN 邊對應的引數初始化為 $1$,其餘的初始化為$0$;
- 對於 attentive learner,讓 $\omega^{(l)} \in \omega$ 中的每個元素都為 $1$。然後,根據度量函數計算特徵級相似度,並通過 sparsification post-processing 得到 kNN 圖;
- 對於 MLP learner 和GNN learner,將嵌入維數設定為 $d$,並將 $\Omega^{(l)} \in \omega$ 初始化為單位矩陣;

learned_adj = graph_learner(features)
對於 structure refinement task ,採用 原始圖鄰接矩陣 $A$,即 $\mathcal{G}_{a}=\left(\mathbf{A}_{a}, \mathbf{X}\right)=(\mathbf{A}, \mathrm{X})$。
對於 structure inference task,採用單位矩陣 $I$ 作為圖結構,即 $\mathcal{G}_{a}=\left(\mathrm{A}_{a}, \mathrm{X}\right)=(\mathrm{I}, \mathrm{X})$。

if args.gsl_mode == 'structure_inference':
if args.sparse:
anchor_adj_raw = torch_sparse_eye(features.shape[0])
else:
anchor_adj_raw = torch.eye(features.shape[0])
elif args.gsl_mode == 'structure_refinement':
if args.sparse:
anchor_adj_raw = adj_original
else:
anchor_adj_raw = torch.from_numpy(adj_original)
3.3.2 Data Augmentation
資料增強:Feature mask 和 Edge drop。
為干擾節點特徵,隨機選擇一部分特徵維度,並用 $0$ 掩蔽它們。
形式上,對於給定的特徵矩陣 $\mathbf{X}$,首先取樣一個掩蔽向量 $\mathbf{m}^{(x)} \in\{0,1\}^{d}$,其中每個元素都來自一個獨立的概率為伯努利分佈 $p^{(x)}$。然後,用 $\mathbf{m}^{(x)}$ 掩碼每個節點的特徵向量:
$\overline{\mathbf{X}}=\mathcal{T}_{f m}(\mathbf{X})=\left[\mathbf{x}_{1} \odot \mathbf{m}^{(x)}, \cdots, \mathbf{x}_{n} \odot \mathbf{m}^{(x)}\right]^{\top}\quad\quad\quad(9)$
其中,$\bar{X}$ 為增廣特徵矩陣,$\mathcal{T}_{f m}(\cdot)$ 為特徵掩蔽變換,$x_{i}$ 為 $X$ 的第 $i$ 行向量的轉置。
Edge dropping
$\overline{\mathbf{A}}=\mathcal{T}_{e d}(\mathbf{A})=\mathbf{A} \odot \mathbf{M}^{(a)}\quad\quad\quad(10)$
其中 $\overline{\mathbf{A}}$ 為增廣鄰接矩陣,$\mathcal{T}_{e d}(\cdot)$ 為邊丟棄變換。
在 SUBLIME 中,利用這兩種增強方案在 learner view 和 anchor view 上生成增強圖:
$\overline{\mathcal{G}}_{l}=\left(\mathcal{T}_{e d}(\mathrm{~S}), \mathcal{T}_{f m}(\mathbf{X})\right), \overline{\mathcal{G}}_{a}=\left(\mathcal{T}_{\text {ed }}\left(\mathbf{A}_{a}\right), \mathcal{T}_{f m}(\mathbf{X})\right)\quad\quad\quad(11)$
其中,$\overline{\mathcal{G}}_{l}$ 和 $\overline{\mathcal{G}}_{a}$ 分別為增強的 learner view 和 anchor view。
為了在兩個檢視中獲得不同的上下文,兩個檢視的 Feature masking 採用了不同的概率 $p_{l}^{(x)} \neq p_{a}^{(x)}$。對於 Edge dropping,由於兩個檢視的鄰接矩陣已經有了顯著的不同,因此使用相同的丟棄概率 $p_{l}^{(a)}=p_{a}^{(a)}=p^{(a)}$。
3.3.3 Node-level Contrastive Learning
在獲得兩個增廣圖檢視後,執行節點級對比學習,以最大化它們之間的 MI。在 SUBLIME 採用了一個來自 SimCLR[6] 的簡單的對比學習框架,由以下組成部分組成:
一個基於 GNN 的編碼器 $f_{\theta}(\cdot)$ 提取增廣圖 $\overline{\mathcal{G}}_{l}$ 和 $\overline{\mathcal{G}}_{a}$ 的節點層表示:
$\mathbf{H}_{l}=f_{\theta}\left(\overline{\mathcal{G}}_{l}\right), \mathbf{H}_{a}=f_{\theta}\left(\overline{\mathcal{G}}_{a}\right)\quad\quad\quad(12)$
其中,$\theta$ 為編碼器 $f_{\theta}(\cdot)$ 的引數,$\mathrm{H}_{l}, \mathrm{H}_{a} \in \mathbb{R}^{n \times d_{1}}$( $d_{1}$ 為表示維數)分別為 learner/anchor views 的節點表示矩陣。在 SUBLIME 中,使用 GCN 作為我們的編碼器,並將其層數 $L_{1}$ 設定為 $2$。
MLP-based projector
在編碼器之後,一個帶有 $L_{2}$ 層的 MLP 投影頭 $g_{\varphi}(\cdot)$ 將表示對映到另一個潛在空間,在其中計算對比損失:
$\mathbf{Z}_{l}=g_{\varphi}\left(\mathbf{H}_{l}\right), \mathbf{Z}_{a}=g_{\varphi}\left(\mathbf{H}_{a}\right)\quad\quad\quad(13)$
其中,$\varphi$ 為投影頭 $g_{\varphi}(\cdot)$ 的引數,$\mathbf{Z}_{l}, \mathbf{Z}_{a} \in \mathbb{R}^{n \times d_{2}}(d_{2}$( $d_{2}$ 為投影維數)分別為 learner/anchor views 的投影后的嵌入矩陣。
Node-level contrastive loss function
一個對比損失 $\mathcal{L}$ 被利用來強制最大化在兩個檢視上同一節點 $v_{i}$ 上的投影 $z_{l, i}$ 和 $z_{a, i}$ 之間的一致性。在我們的框架中,應用了對稱歸一化溫度尺度交叉熵損失(NT-Xent)[29,35]:
${\large \begin{array}{l}\mathcal{L}=\frac{1}{2 n} \sum_{i=1}^{n}\left[\ell\left(z_{l, i}, z_{a, i}\right)+\ell\left(z_{a, i}, z_{l, i}\right)\right] \\\ell\left(z_{l, i}, z_{a, i}\right)=\log \frac{e^{\operatorname{sim}\left(\mathrm{z}_{l, i}, \mathrm{z}_{a, i}\right) / t}}{\sum_{k=1}^{n} e^{\operatorname{sim}\left(\mathrm{z}_{l, i}, \mathrm{z}_{a, k}\right) / t}}\end{array}} \quad\quad\quad(14)$
3.4 Structure Bootstrapping Mechanism
使用由 $\mathbf{A}$ 或 $I$ 定義的固定的 Anchor 鄰接矩陣 $\mathbf{A}_{a}$,SUBLIME 可以通過最大化兩個檢視之間的MI來學習圖結構 $S$。
然而,使用固定的$\mathbf{A}_{a}$ 可能會導致幾個問題:
-
- Inheritance of error information。由於 $\mathbf{A}_{a}$ 是直接從輸入資料中得到的,所以它會攜帶原始圖的一些自然噪聲(例如,缺失或冗餘的邊)。如果在學習過程中不消除噪聲,學習到的結構最終將繼承它;
- Lack of persistent guidance。一個固定的錨點圖包含有限的資訊來指導GSL。一旦圖學習者捕獲了這些資訊,模型將很難在以下的訓練步驟中獲得有效的監督;
- Overfitting the anchor structure。在使兩個檢視之間的一致性最大化的學習目標的驅動下,學習到的結構傾向於過度擬合固定的錨定結構,從而導致與原始資料相似的測試效能;
受基於 bootstrap 的演演算法 [5,14,37] 的啟發,本文設計了一個 structure bootstrapping mechanism,提供一個 bootstrap 的 Anchor 檢視作為學習目標。本文解決方案的核心思想是通過學習到的 $S$ 緩慢更新錨定結構 $\mathbf{A}_{a}$,而不是保持 $\mathbf{A}_{a}$ 不變。即,給定衰減速率 $\tau \in[0,1]$,錨定結構 $\mathbf{A}_{a}$ 每 $c$ 次迭代更新如下:
$\mathbf{A}_{a} \leftarrow \tau \mathbf{A}_{a}+(1-\tau) \mathrm{S} \quad\quad\quad(15)$
隨著更新過程的進行,$\mathbf{A}_{a}$ 中一些噪聲邊的權值逐漸減小,減輕了它們對結構學習的負面影響。同時,由於學習目標 $\mathbf{A}_{a}$ 在訓練階段發生了變化,它總是可以包含更有效的資訊來指導拓撲的學習,過擬合問題自然得到了解決。更重要的是,Structure Bootstrapping Mechanism 利用學習到的知識來提高學習目標,從而推動模型不斷髮現越來越最優的圖結構。此外,slow-moving average($\tau \ge 0.99$)的更新確保了訓練的穩定性。
4 Experiments
資料集
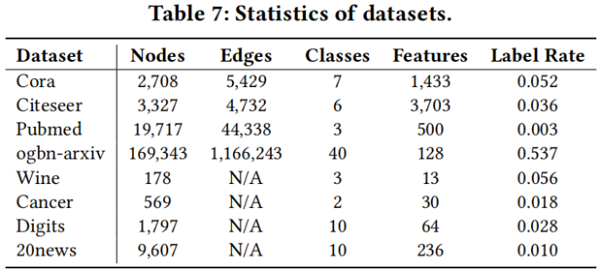
Node classification in structure inference scenario
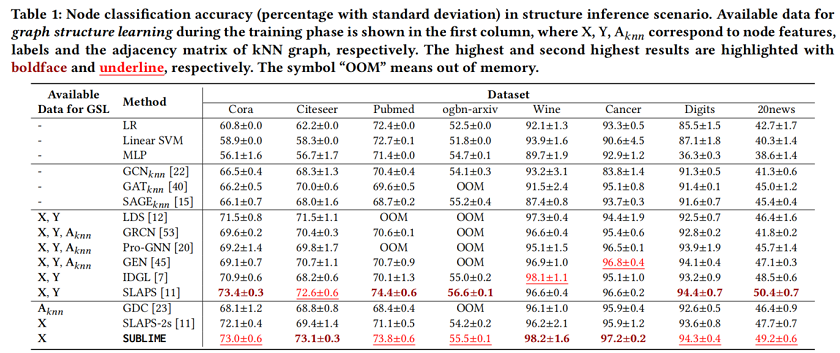
Node classification in structure refinement scenario
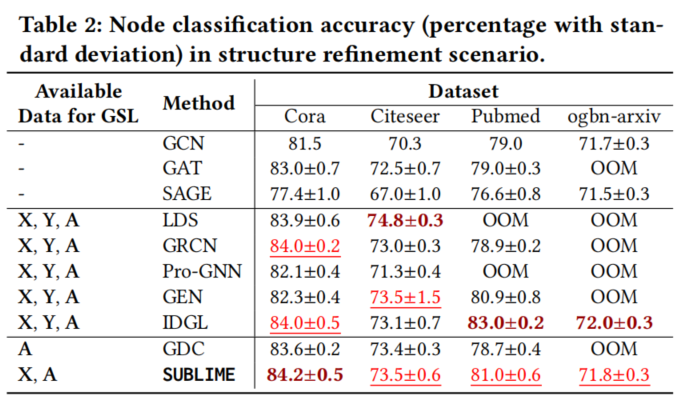
Node clustering in structure refinement scenario
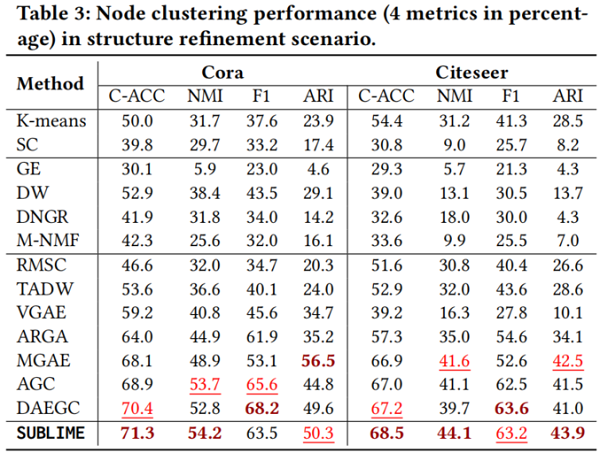
5 Conclusion
本文對無監督圖結構學習問題進行了首次研究。為了解決這個問題,我們設計了一種新的方法,即崇高的方法,它能夠利用資料本身來生成最優的圖結構。為了學習圖的結構,我們的方法使用對比學習來最大限度地提高學習到的拓撲結構和一個自增強的學習目標之間的一致性。大量的實驗證明了學習結構的優越性和合理性。
因上求緣,果上努力~~~~ 作者:Learner-,轉載請註明原文連結:https://www.cnblogs.com/BlairGrowing/p/16339629.html
