分散式機器學習：PageRank演演算法的並行化實現（PySpark）

1. PageRank的兩種序列迭代求解演演算法

我們在部落格《數值分析：冪迭代和PageRank演演算法(Numpy實現)》演演算法中提到過用冪法求解PageRank。
給定有向圖

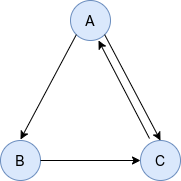
我們可以寫出其馬爾科夫概率轉移矩陣\(M\)(第\(i\)列對應對\(i\)節點的鄰居並沿列歸一化)

\[\left(\begin{array}{lll} 0 & 0 & 1 \\ \frac{1}{2} & 0 & 0 \\ \frac{1}{2} & 1 & 0 \end{array}\right) \]

然後我們定義Google矩陣為

\[G=\frac{q}{n} E+(1-q) M \]

此處\(q\)為上網者從一個頁面轉移到另一個隨機頁面的概率（一般為0.15），\(1-q\) 為點選當前頁面上連結的概率，\(E\)為元素全1的\(n\times n\) 矩陣( \(n\) 為節點個數)。

而PageRank演演算法可以視為求解Google矩陣佔優特徵值（對於隨機矩陣而言，即1）對應的特徵向量。設初始化Rank向量為 \(x\)（ \(x_i\) 為頁面\(i\)的Rank值），則我們可以採用冪法來求解：

\[x_{t+1}=G x_{t} \]

(每輪迭代後要歸一化)

現實場景下的圖大多是稀疏圖，即\(M\)是稀疏矩陣。冪法中計算 \((1-q)Mx_t\) ，對於節點 \(i\) 需使用reduceByKey()（key為節點編號）操作。計算 \(\frac{q}{n}{E}x_t\) 則需要對所有節點的Rank進行reduce()操作，操作頗為繁複。

PageRank還有一種求解演演算法（名字就叫「迭代演演算法」），它的迭代形式如下：

\[x_{t+1} = \frac{q}{n}\bm{1} + (1-q)Mx_t \]

可以看到，這種迭代方法就規避了計算 \(\frac{q}{n}Ex_t\)，通訊開銷更小。我們接下來就採用這種迭代形式。

2. 圖劃分的兩種方法

目前對圖演演算法進行並行化的主要思想是將大圖切分為多個子圖，然後將這些子圖分佈到不同的機器上進行平行計算，在必要時進行跨機器通訊同步計算得出結果。學術界和工業界提出了多種將大圖切分為子圖的劃分方法，主要包括兩種，邊劃分(Edge Cut)和點劃分(Vertex Cut)。

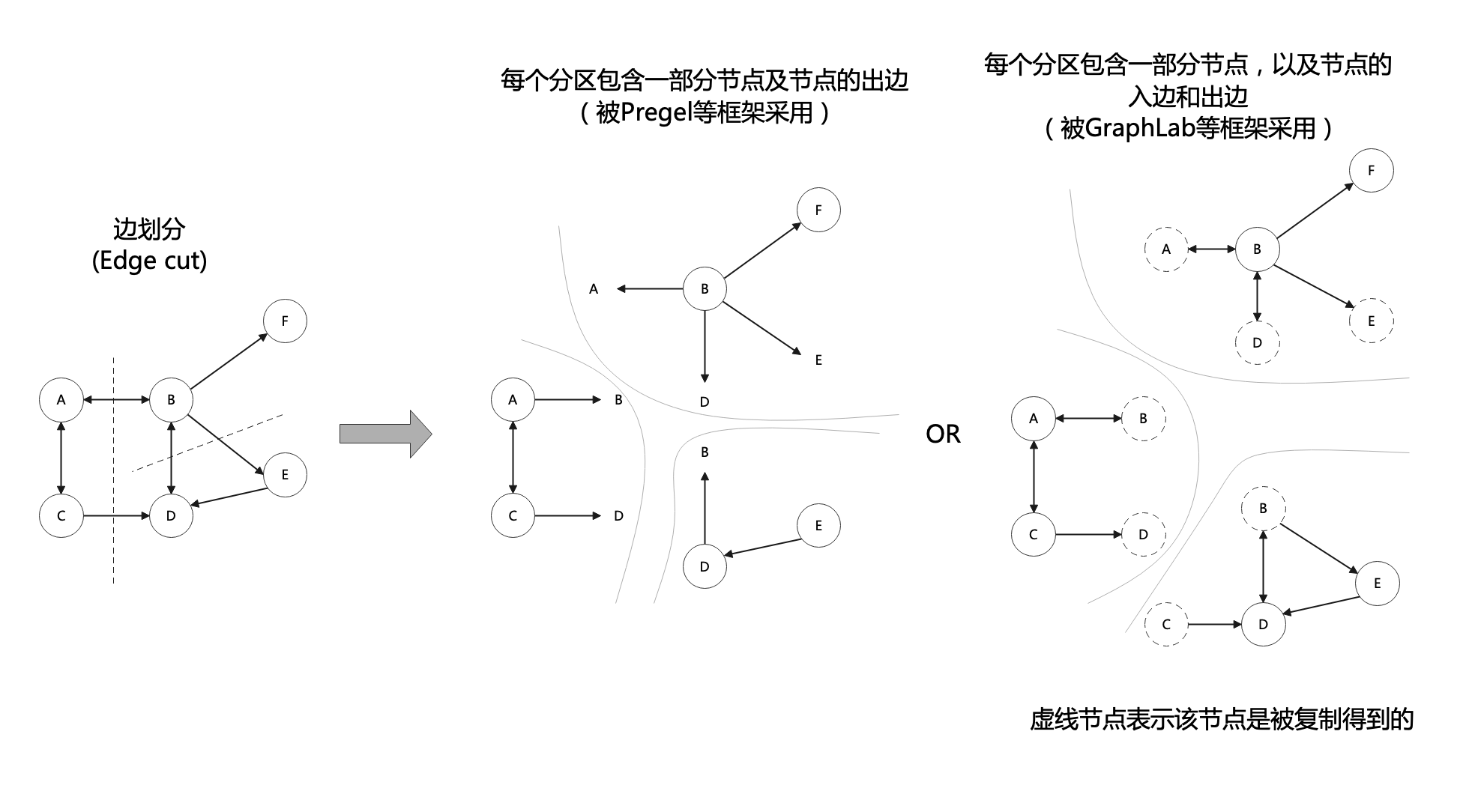
2.1 邊劃分

如下圖所示，邊劃分是對圖中某些邊進行切分。具體在Pregel^[1]圖計算框架中，每個分割區包含一些節點和節點的出邊；在GraphLab^[2]圖計算框架中，每個分割區包含一些節點、節點的出邊和入邊，以及這些節點的鄰居節點。邊劃分的優點是可以保留節點的鄰居資訊，缺點是容易出現劃分不平衡，如對於度很高的節點，其關聯的邊都被劃分到一個分割區中，造成其他分割區中的邊可能很少。另外，如下圖最右邊的圖所示，邊劃分可能存在邊冗餘。

2.2 點劃分

如下圖所示，點劃分是對圖中某些點進行切分，得到多個圖分割區，每個分割區包含一部分邊，以及與邊相關聯的節點。具體地，PowerGraph^[3]，GraphX^[4]等框架採用點劃分，被劃分的節點存在多個分割區中。點劃分的優缺點與邊劃分的優缺點正好相反，可以將邊較為平均地分配到不同機器中，但沒有保留節點的鄰居關係。

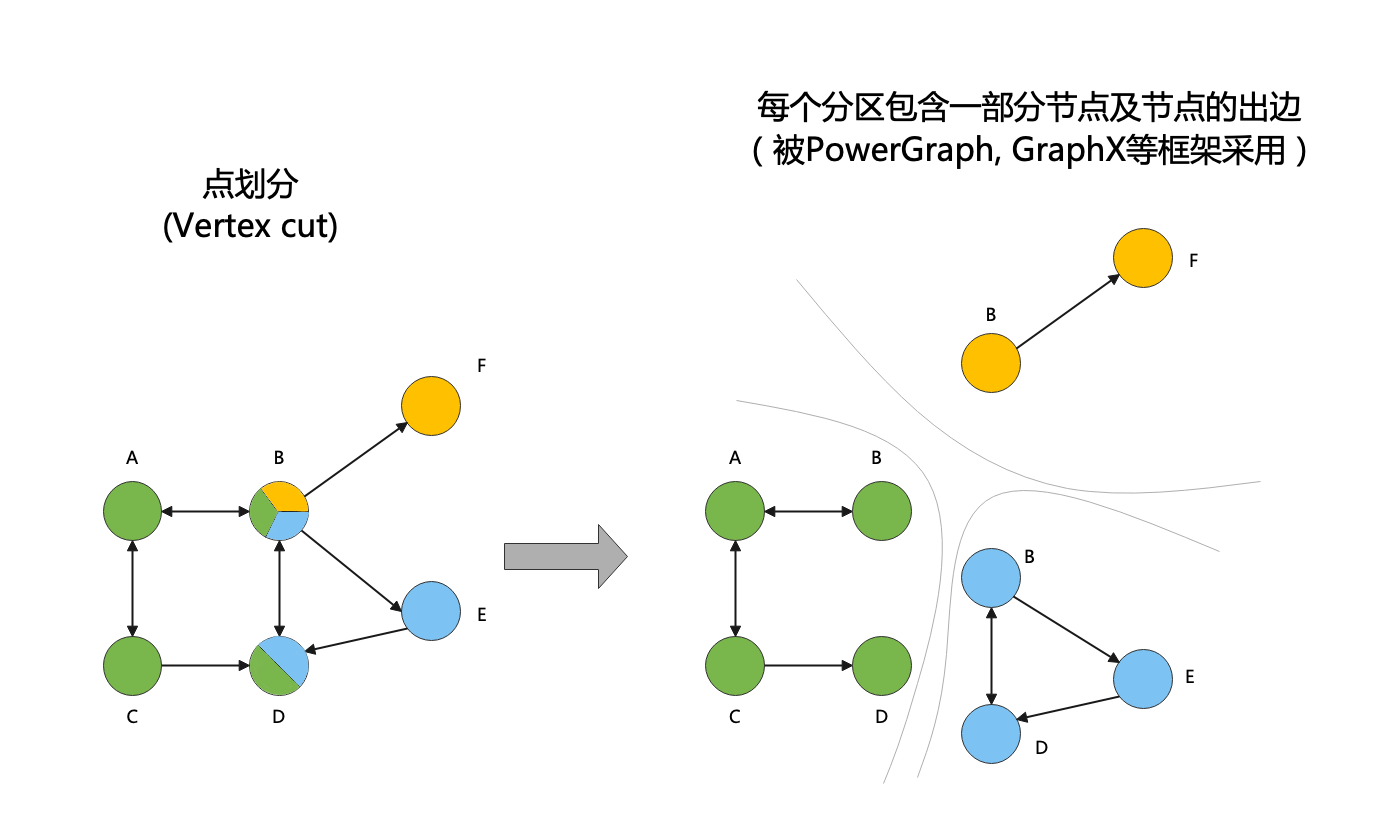
總而言之，邊劃分將節點分佈到不同機器中(可能劃分不平衡)，而點劃分將邊分佈到不同機器中(劃分較為平衡)。接下來我們使用的演演算法為類似Pregel的劃分方式，使用邊劃分。我們下面的演演算法是簡化版，沒有處理懸掛節點的問題。

3. 對迭代演演算法的並行化

我們將Rank向量用均勻分佈初始化（也可以用全1初始化，不過就不再以概率分佈的形式呈現），設分割區數為3，演演算法總體迭代流程可以表示如下：

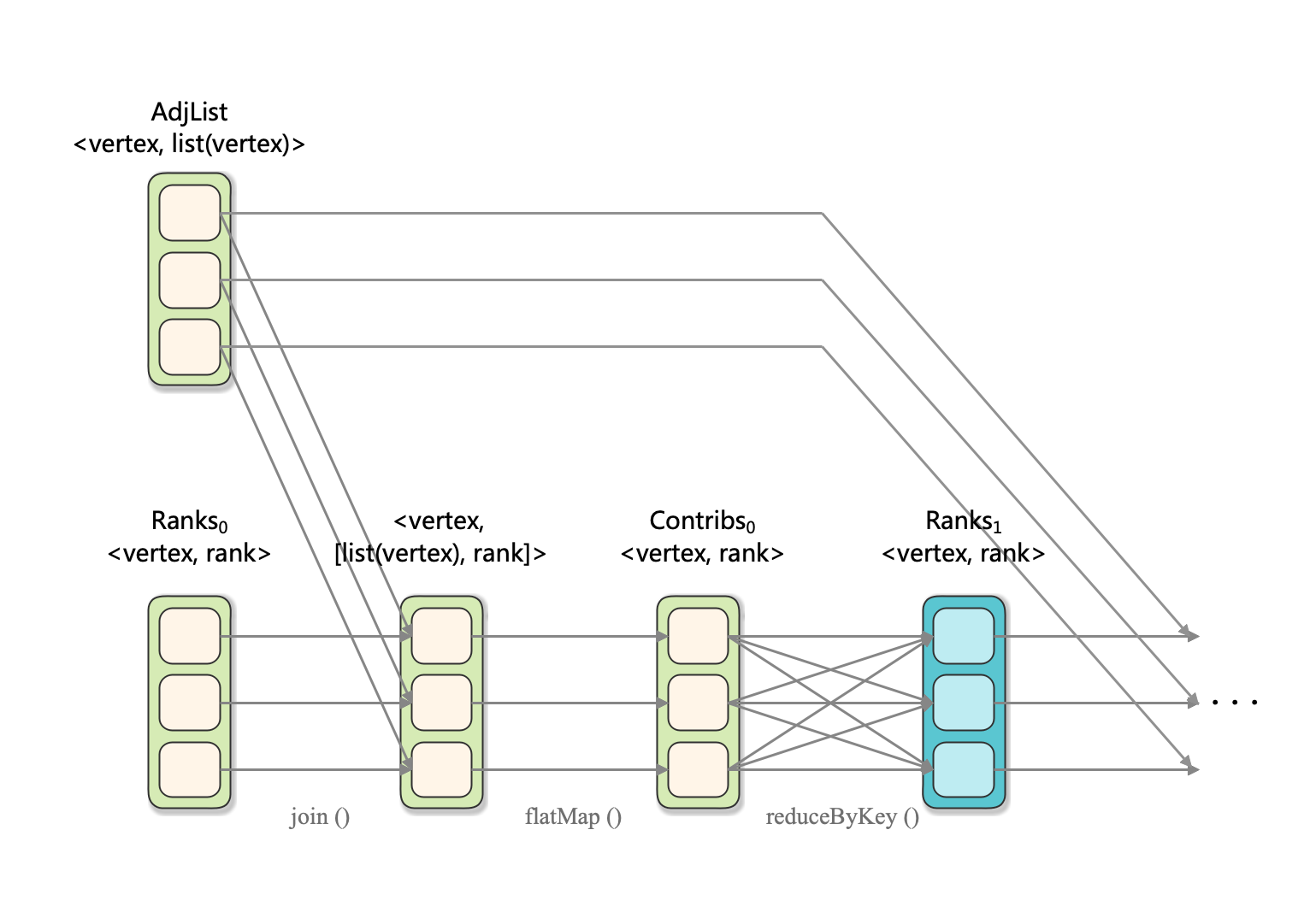
注意，圖中flatMap()步驟中，節點\(i\)計算其contribution（貢獻度）：\((x_t)_i/|\mathcal{N}_i|\)，並將貢獻度傳送到鄰居集合\(\mathcal{N}_i\)中的每一個節點。之後，將所有節點收到的貢獻度使用reduceByKey()（節點編號為key）規約後得到向量\(\hat{x}\)，和序列演演算法中\(Mx_t\)的對應關係如下圖所示：

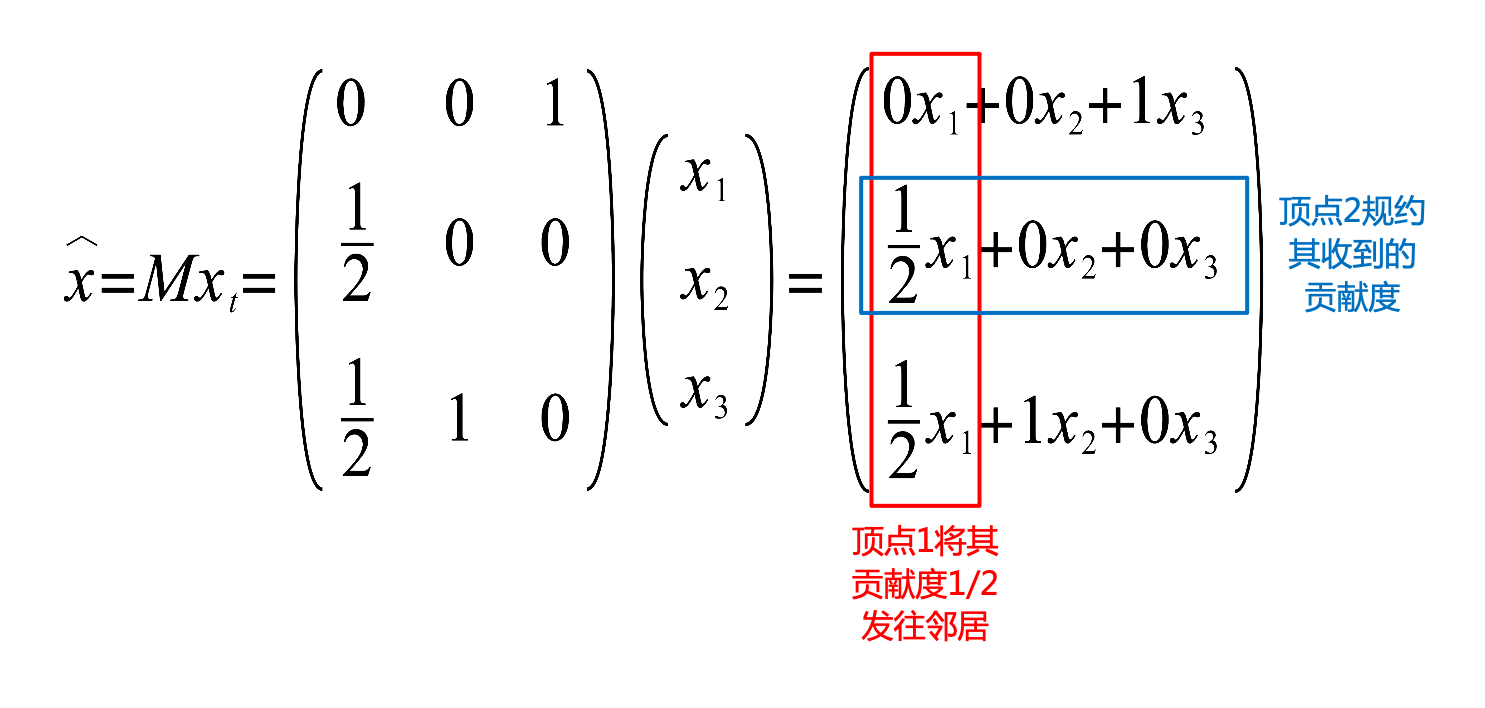
並按照公式\(x_{t+1} = \frac{q}{n} + (1-q)\hat{x}\)來計算節點的Rank向量。然後繼續下一輪的迭代過程。

4. 程式設計實現

用PySpark對PageRank進行並行化程式設計實現，程式碼如下：

import re
import sys
from operator import add
from typing import Iterable, Tuple

from pyspark.resultiterable import ResultIterable
from pyspark.sql import SparkSession

n_slices = 3  # Number of Slices
n_iterations = 10  # Number of iterations
q = 0.15 #the default value of q is 0.15

def computeContribs(neighbors: ResultIterable[int], rank: float) -> Iterable[Tuple[int, float]]:
    # Calculates the contribution(rank/num_neighbors) of each vertex, and send it to its neighbours.
    num_neighbors = len(neighbors)
    for vertex in neighbors:
        yield (vertex, rank / num_neighbors)

if __name__ == "__main__":
    # Initialize the spark context.
    spark = SparkSession\
        .builder\
        .appName("PythonPageRank")\
        .getOrCreate()

    # link: (source_id, dest_id)
    links = spark.sparkContext.parallelize(
        [(1, 2), (1, 3), (2, 3), (3, 1)],
        n_slices
    )                       

    # drop duplicate links and convert links to an adjacency list.
    adj_list = links.distinct().groupByKey().cache()

    # count the number of vertexes
    n_vertexes = adj_list.count()

    # init the rank of each vertex, the default is 1.0/n_vertexes
    ranks = adj_list.map(lambda vertex_neighbors: (vertex_neighbors[0], 1.0/n_vertexes))

    # Calculates and updates vertex ranks continuously using PageRank algorithm.
    for t in range(n_iterations):
        # Calculates the contribution(rank/num_neighbors) of each vertex, and send it to its neighbours.
        contribs = adj_list.join(ranks).flatMap(lambda vertex_neighbors_rank: computeContribs(
            vertex_neighbors_rank[1][0], vertex_neighbors_rank[1][1]  # type: ignore[arg-type]
        ))

        # Re-calculates rank of each vertex based on the contributions it received
        ranks = contribs.reduceByKey(add).mapValues(lambda rank: q/n_vertexes + (1 - q)*rank)

    # Collects all ranks of vertexs and dump them to console.
    for (vertex, rank) in ranks.collect():
        print("%s has rank: %s." % (vertex, rank))

    spark.stop()

執行結果如下：

1 has rank: 0.38891305880091237.  
2 has rank: 0.214416470596171.
3 has rank: 0.3966704706029163.

該Rank向量與我們採用序列冪法得到的Rank向量 \(R=(0.38779177,0.21480614,0.39740209)^{T}\) 近似相等，說明我們的並行化演演算法執行正確。

參考

[1] Malewicz G, Austern M H, Bik A J C, et al. Pregel: a system for large-scale graph processing[C]//Proceedings of the 2010 ACM SIGMOD International Conference on Management of data. 2010: 135-146.
[2] Low Y, Gonzalez J, Kyrola A, et al. Distributed graphlab: A framework for machine learning in the cloud[J]. arXiv preprint arXiv:1204.6078, 2012.
[3] Gonzalez J E, Low Y, Gu H, et al. {PowerGraph}: Distributed {Graph-Parallel} Computation on Natural Graphs[C]//10th USENIX symposium on operating systems design and implementation (OSDI 12). 2012: 17-30.
[4] Spark: GraphX Programming Guide
[5] GiHub: Spark官方Python樣例
[6] 許利傑，方亞芬. 巨量資料處理框架Apache Spark設計與實現[M]. 電子工業出版社, 2021.
[7] Stanford CME 323: Distributed Algorithms and Optimization (Lecture 15)
[8] wikipedia: PageRank
[9] 李航. 統計學習方法(第2版)[M]. 清華大學出版社, 2019.
[10] Timothy sauer. 數值分析(第2版)[M].機械工業出版社, 2018.