使用並查集處理集合的合併和查詢問題
作者:Grey
原文地址:使用並查集處理集合的合併和查詢問題
要解決的問題
有若干個樣本a、b、c、d…,假設型別都是V,在並查集中一開始認為每個樣本都在單獨的集合裡,使用者可以在任何時候呼叫如下兩個方法 :
方法1:查詢樣本x和樣本y是否屬於一個集合,即:
boolean isSameSet(V x,V y);
方法2:把x和y各自所在集合的所有樣本合併成一個集合,即:
void union(V x, V y)
但是,isSameSet和union方法的代價越低越好,在這兩個方法呼叫非常頻繁的情況下,這兩個方法最好能做到O(1)的時間複雜度。
資料結構設計
節點型別定義如下:
private static class Node<V> {
private final V value;
public Node(V value) {
this.value = value;
}
}
但是每個節點都有一條往上指的指標,節點a往上找到的頭節點,叫做a所在集合的代表節點,查詢x和y是否屬於同一個集合,就是看看找到的代表節點是不是一個,如果代表節點是同一個,說明這兩個節點就是在同一集合中,把x和y各自所在集合的所有點合併成一個集合,只需要某個集合的代表點掛在另外一個集合的代表點的下方即可。
我們可以使用三張雜湊表:
// 快速找到某個節點是否存在
private HashMap<V, Node<V>> nodeMap;
// 找到某個節點的父節點
private HashMap<Node<V>, Node<V>> parentMap;
// 每個代表節點代表的節點個數
private HashMap<Node<V>, Integer> sizeMap;
其中的parentMap就充當了找代表節點的責任,查詢任何一個節點x的代表節點,只需要呼叫如下方法即可:
parentMap.get(x)
現在以一個實際例子來說明並查集的基本操作,假設現在有如下的樣本,現在每個樣本都是獨立的集合,每個樣本各自都是自己的代表節點,
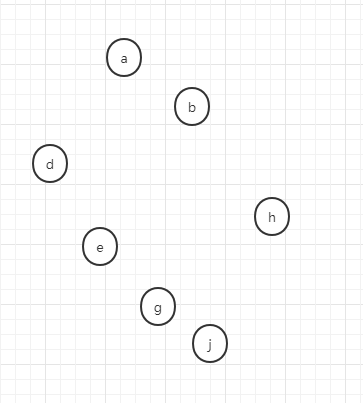
假設我做如下操作,
第一個操作,將a和b合併成一個集合
union(a,b)
操作完畢後,a和b將做如下合併操作,合併後,先隨便以一個點作為合併集合的代表節點,假設代表節點用藍色表示
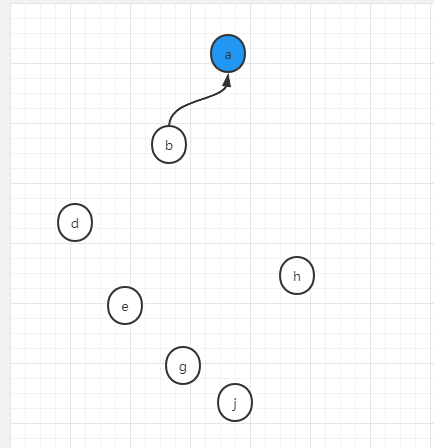
第二個操作,將b和d合併成一個集合
union(b,d)
此時,b將找到其代表節點a,d將找到其代表節點也就是它本身d,將d和a合併在一起,假設我們用a去連d,然後將a,b,d這個集合的代表節點更新為d
即:
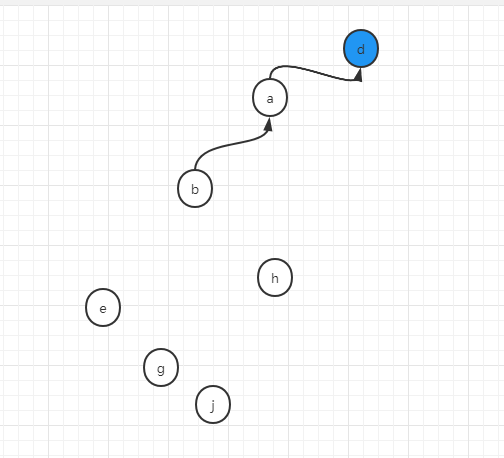
第三個操作,將b和h合併成一個集合
union(b,h)
此時,b將找到其代表節點d,h將找到其代表節點也就是它本身h,將d和h合併在一起,假設我們用d去連h,然後將a,b,d,h這個集合的代表節點更新為h,如下圖
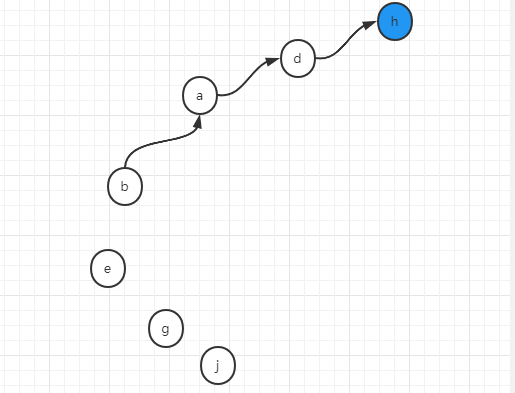
假設e,g,j都做同樣的合併
union(e,g)
union(g,j)
結果如下
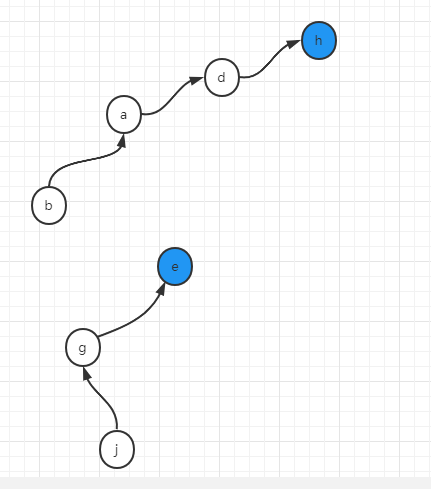
最後,假設我們呼叫
union(j,b)
即:將j所在集合和b所在集合合併在一起,那麼就需要j一直向上找到其代表節點e,b向上找到其代表節點h,然後將兩個代表節點連線起來即可,比如可以是這樣
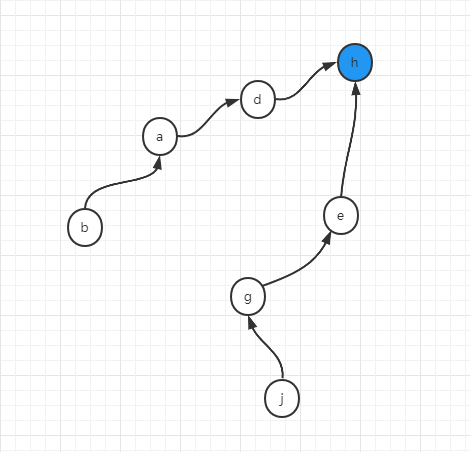
並查集的優化
根據如上流程範例,我們可以瞭解到一個問題,就是如果兩個節點距離各自的代表節點比較長,比如上面的b點距離其代表節點h就比較長,隨著資料量增多,這會極大影響效率,所以,並查集的第一個優化就是:
節點往上找代表點的過程,把沿途的鏈變成扁平的
舉例說明,我們上述例子中的第二個操作,將b和d合併成一個集合
union(b,d)
此時,b將找到其代表節點a,d將找到其代表節點也就是它本身d,將d和a合併在一起,假設我們用a去連d,然後將a,b,d這個集合的代表節點更新為d
即:

如果做了扁平化操作,那麼在合併b和d的過程中,不是簡單的用a去連d,而是將a節點的所有下屬節點都直連d,所以就變成了:
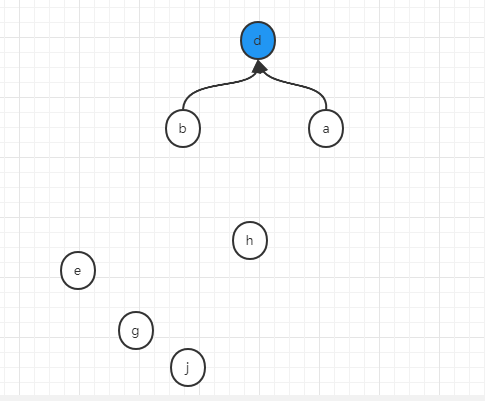
如果我們每一次做union操作,都順便做一次扁平化,那麼上述例子在最後一步執行之前,應該是這樣的狀態
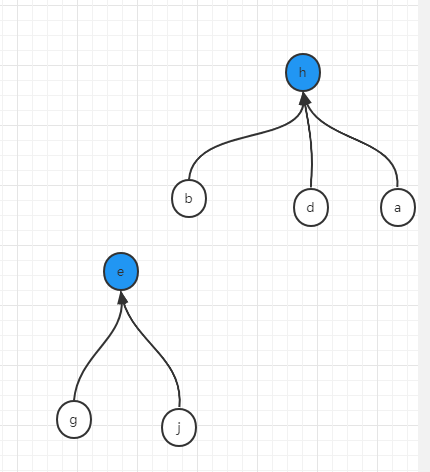
如果變成了這樣的狀態,那麼每次找自己的代表節點這個操作,只需要往上看一次就可以。這在具體程式碼實現上使用了佇列,即,將某個節點往上直到代表節點的所有元素都記錄在佇列裡面,然後將記錄在佇列中的所有元素的父節點都指向代表節點。
private Node<V> findFather(Node<V> node) {
// 沿途節點都放佇列裡面
// 然後將佇列元素做扁平化操作
Queue<Node<V>> queue = new LinkedList<>();
while (node != parentMap.get(node)) {
queue.offer(node);
node = parentMap.get(node);
}
while (!queue.isEmpty()) {
// 優化2:扁平化操作
parentMap.put(queue.poll(), node);
}
return node;
}
並查集的第二個優化是:
小集合掛在大集合的下面
舉例說明,假設我們經過了若干次的union之後,形成了如下兩個集合,顯然,h為代表節點的集合是小集合,只有四個元素,而以e為代表節點的集合是相對來說就是大集合。
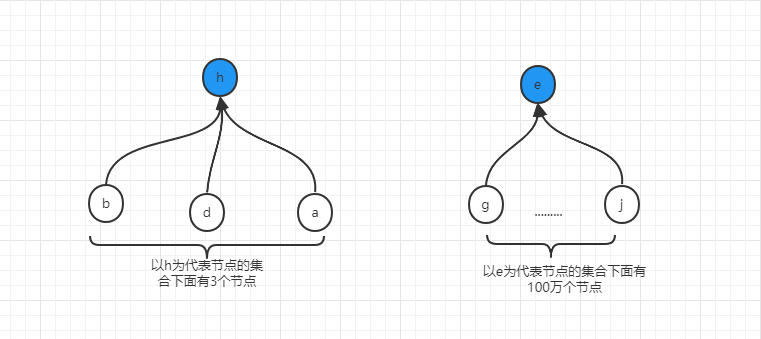
如果此時,要合併b節點所在集合(代表節點為h)和j幾點所在集合(代表節點為e),那麼就面臨到底應該遷移e及其下面所有的點到h上,還是應該遷移h及下面所有的點到e上,從兩個集合的數量上來說,遷移h集合到e上的代價要比遷移e到h上的代價要低的多,所以這就是並查集的第二個優化。
經過了如上兩個優化,並查集中的union或者isSameSet方法如果呼叫很頻繁,那麼單次呼叫的代價為O(1),兩個方法都如此。
完整程式碼
package snippet;
import java.util.HashMap;
import java.util.LinkedList;
import java.util.List;
import java.util.Queue;
public class Code_0049_UnionFind {
public static class UnionFind<V> {
// 快速找到某個節點是否存在
private HashMap<V, Node<V>> nodeMap;
// 找到某個節點的父節點
private HashMap<Node<V>, Node<V>> parentMap;
// 每個代表節點代表的節點個數
private HashMap<Node<V>, Integer> sizeMap;
public UnionFind(List<V> values) {
nodeMap = new HashMap<>();
parentMap = new HashMap<>();
sizeMap = new HashMap<>();
for (V v : values) {
Node<V> n = new Node<>(v);
nodeMap.put(v, n);
parentMap.put(n, n);
sizeMap.put(n, 1);
}
}
// v1,v2必須是已經存在nodeMap中的元素
public void union(V v1, V v2) {
if (!nodeMap.containsKey(v1) || !nodeMap.containsKey(v2)) {
return;
}
if (!isSameSet(v1, v2)) {
Node<V> v1Parent = nodeMap.get(v1);
Node<V> v2Parent = nodeMap.get(v2);
Node<V> small = sizeMap.get(v1Parent) > sizeMap.get(v2Parent) ? v2Parent : v1Parent;
Node<V> large = small == v1Parent ? v2Parent : v1Parent;
sizeMap.put(large, sizeMap.get(large) + sizeMap.get(small));
// 優化1:小集合掛在大集合下面
parentMap.put(small, large);
parentMap.remove(small);
}
}
private Node<V> findFather(Node<V> node) {
Queue<Node<V>> queue = new LinkedList<>();
while (node != parentMap.get(node)) {
queue.offer(node);
node = parentMap.get(node);
}
while (!queue.isEmpty()) {
// 優化2:扁平化操作
parentMap.put(queue.poll(), node);
}
return node;
}
public boolean isSameSet(V v1, V v2) {
if (!nodeMap.containsKey(v1) || !nodeMap.containsKey(v2)) {
return false;
}
return findFather(nodeMap.get(v1)) == findFather(nodeMap.get(v2));
}
private static class Node<V> {
private final V value;
public Node(V value) {
this.value = value;
}
}
}
}