關於雜湊
雜湊表,也稱雜湊表,是一種高效的資料結構。它的最大優點就是把資料儲存和查詢所消耗的時間大大降低,幾乎可以看成是 O(1)的,而代價是消耗比較多的記憶體。
他的基本實現原理就是將輸入以某種方式轉化為固定長度的輸出,該輸出就是雜湊值:
舉個例子,比較兩個字串是否相同,可以將所有的字母轉換為數位1到26,將字串用數位累加求和再取餘的方式求出雜湊值,通過比較兩者雜湊值是否相等來判斷兩字串是否相等
我們可以用字首和的思想來計算每個字串的雜湊值:
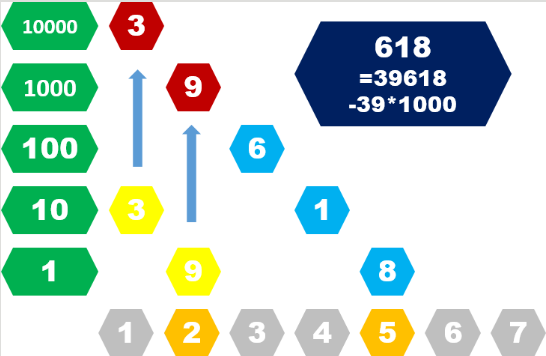
通過這個例子我們就很好地解決了每個字串的雜湊值:


比如說輸入一個字串,輸入a,b,c,d,嘗試比較[a,b],[c,d]兩個子字串是否相同
下面給出核心程式碼:
1 string s; // s 為字串 2 int f[N], g[N]; // f 為字首和,g[i] 為 D 的 i 次方 3 void prehash(int n) // 預處理雜湊值 4 {// 預處理時,注意到數位可能很大,對一個數 MD 取模 5 f[0] = s[0]; // f 字首和預處理 6 for(int i=1; i<=n; i++) 7 { 8 f[i] = (1LL * f[i-1] * D + s[i-1]) % MD; 9 } 10 g[0] = 1; // g:D 次方預處理 11 for(int i=1; i<=n; i++) 12 { 13 g[i] = 1LL * g[i-1] * D % MD; 14 } 15 } 16 int hash(int l, int r) // 計算區間 [l,r] 的雜湊值 17 { 18 int a = f[r]; 19 int b = 1LL * f[l-1] * g[r-l+1] % MD; // 記得乘上次方 20 return (a - b + MD) % MD; // 字首和相減 21 // 有可能結果小於 0,加上一個 MD 將其變為正數 22 } 23 if(hash(a, b) == hash(c, d)) // 字串 [a,b] 與字串 [c,d] 匹配
這種方法固然很不錯,但是也有一個小問題:兩個不同的資料無法保證其雜湊值一定不同,也就會判斷錯誤,這種情況叫做雜湊衝突
那麼如何解決這樣的衝突呢???這裡介紹兩種方法:
1、拉鍊法(鏈地址法):
就是將具有相同雜湊值的資料存在一個連結串列中,查詢某一元素是否在雜湊表時,就求出待判斷的那個元素的雜湊值,並在雜湊表中找到相應位置的地址,搜尋這條鏈上的元素並判斷是否相等即可,連結串列結構如下圖所示:
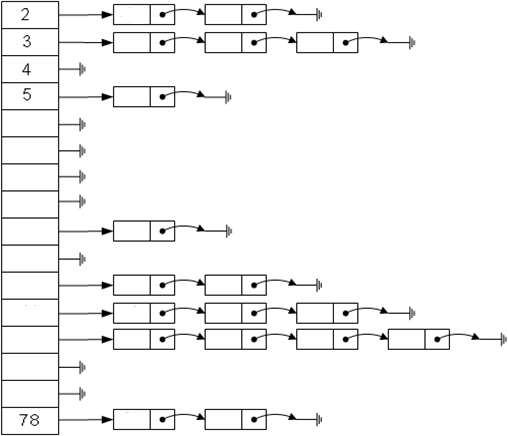
核心程式碼如下:
1 //鏈地址法 2 vector<int> hash_array[N]; 3 // hash_array:每個位置用一個 vector 來維護 4 void push2(int x) 5 { 6 int y = x % N; // 計算初始位置 7 for(int i=0; i<hash_array[y].size(); i++) if(hash_array[y][i] == x) // 如果之前已經出現過了 8 { 9 cout << x << "?has?occured?before!" << endl; 10 return; // 標記已經出現過 11 } 12 // 如果之前沒有出現過,將 x 加入表中 13 hash_array[y].push_back(x); 14 cout << x << "?inserted." << endl; 15 }
2.順序詢址法:
就是當有兩個元素的雜湊值出現重複的時候,將後輸入的元素往後放(如果後面有空的話),當然,如果後面也被佔領了,就一直往後找,直到有空隙能夠放下為止,
當想要查詢一個元素時,先求出他的雜湊值,找到雜湊表對應的位置,如果不是就一直往後找,如果查詢到了當前位置為空時還沒有找到此元素,那麼這個元素就不存在,輸出no,反之則輸出yes
核心程式碼如下:
//順序定址法 int hash_table[N]; // hash_table 雜湊表:0 位置代表沒有數 void push1(int x) { int y = x % N; // 計算初始位置,N:表的大小 for(; hash_table[y]!=0 && hash_table[y]!=x; ) y = (y+1) % N; // 尋找到一個 0 位置,或者找到自己為止 if(hash_table[y]) cout << x << "?has?occured?before!" << endl; // 如果是自己本身,則之前已經出現過了 else { hash_table[y] = x; // 否則,將 x 加入表中 cout << x << "?inserted." << endl; } }
還有就是雜湊表的常見構造方法,一種經典的叫做求模取餘法(上文也有所體現):
嘗試構造一種雜湊函數:H(key)=key%p
其中p是一個可以自己擬定的值,但儘量要求p<=雜湊表的表長m且p是一個質數。
雜湊有很多的應用,比如:
輸入n個整數,輸入m為存取次數,每次存取是輸入一個數並判斷原序列中是否有這個元素
程式碼如下:
#include<cstdio> #include<iostream> using namespace std; const int N=50000; //定義總共輸入雜湊數位個數 const int b=999979,H=999979;//雜湊取模%數位 int tot,adj[H],nxt[N],num[N]; int top,stk[N]; void init() { //初始化雜湊表 tot=0; while(top) //我們用一個棧儲存下出現過的雜湊值 adj[stk[top--]]=0; } //每次把出現過的雜湊值的連結串列清0,來節省時間 void insert(int key) { //將一個數位插入雜湊表 int h=key%b; //除餘法 for(int e=adj[h];e;e=nxt[e]) if(num[e]==key) //諾連結串列中已存在當前數位則不再存 return; if(!adj[h]) stk[++top]=h; //把第1次出現的雜湊值入棧 nxt[++tot]=adj[h],adj[h]=tot; //建立連結 num[tot]=key; //建立連結表,儲存值等於key的數位。 } bool query(int key) { int h=key%b; for(int e=adj[h];e;e=nxt[e]) //查詢連結 if(num[e]==key) return true; return false; } int main() { int a[10000]; init(); int n,m; cin>>n; for(int i=1;i<=n;++i) { cin>>a[i]; insert(a[i]); } cin>>m; int num; for(int i=1;i<=m;++i) { cin>>num; if(query(num)) printf("yes\n"); else printf("no\n"); } }

1 #include<cstdio> 2 #include<iostream> 3 #include<algorithm> 4 #include<cstring> 5 #define ull unsigned long long 6 using namespace std; 7 const int N=1e4+1; 8 char c[N]; 9 ull a[N]; 10 ull num=131; 11 int ans,n; 12 int prime=233317; 13 ull mod=212370440130137957ll; 14 ull hasha(char s[]) 15 { 16 int len=strlen(c); 17 ull ans=0; 18 for(int i=1;i<=len;i++) 19 { 20 ans=(ans*num+(ull)c[i])%mod+prime; 21 } 22 return ans; 23 } 24 int main() 25 { 26 int n; 27 cin>>n; 28 for(int i=1;i<=n;i++) 29 { 30 cin>>c; 31 a[i]=hasha(c); 32 } 33 sort(a+1,a+n+1); 34 for(int i=1;i<n;i++) 35 { 36 if(a[i]!=a[i+1]) 37 { 38 ans++; 39 } 40 } 41 cout<<ans+1; 42 return 0; 43 }
先記錄到這裡,以後再見吧!