Simple, Fast Malicious Multiparty Private Set Intersection-解讀

文字記錄閱讀該論文的筆記。

這是文章框架，來自視訊。

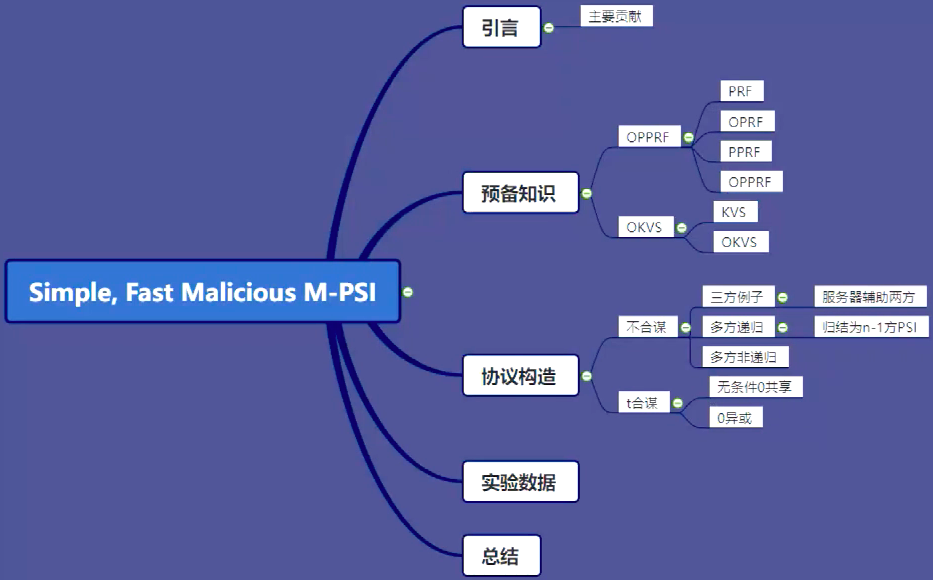
介紹

本文主要解決惡意攻擊下安全的多方PSI，主要用到兩大技術OPPRF和OKVS，構造合謀和不合謀的協定。

基礎知識

OPPRF

這部分在OPRF中有介紹：OPRF

PRF

偽隨機函數，產生的結果類似於偽亂數。

OPRF

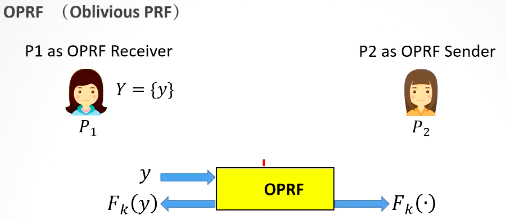
不經意的偽隨機函數，在兩方情況下，\(P_2\)對於\(P_1\)的輸出結果是不知道的，\(P_1\)也不知道\(P_2\)的金鑰\(k\)。

可以根據OPRF構造一個簡單的兩方PSI協定：
（1）\(P_2\)將\(F_k(x)\)傳送給\(P_1\);
（2）\(P_1\)將傳送來的\(F_k(x)\)和自己的\(F_k(y)\)對比是否一樣，如果一樣，則說明\(y\)屬於交集。

PPRF

可程式化的偽隨機函數，即將一組點集\((x,y)\)編碼到PRF中，輸入\(x\)，可以得到對應的\(y\)。

OPPRF

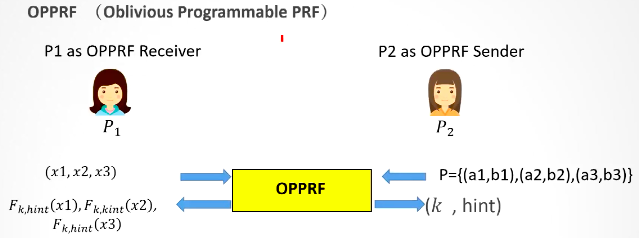
不經意可程式化的偽隨機函數，在兩方情況下，\(P_2\)這邊有一組點集\((a,b)\)，\(P_1\)輸入\(x\)，如果\(x\)在\(a\)中，則返回對應的\(y\)，否則返回一個偽亂數。其中\(P_2\)不知道\(P_1\)的輸入和輸出，\(P_1\)也不知道\(P_2\)的金鑰\(k\)。

這裡的\(hint\)可以看作是一個和輸入有關係的亂數，在以多項式插值實現的方法中：\(P_2\)將這一組點集插入到一個多項式中\(f(.)\)，同時使用\(hint\)去「混淆」該多項式（比如，移動等），然後將混淆後的多項式\(f'(.)\)發給\(P_1\)，進而獲得\(f'(x)\)。

OKVS

KVS

鍵值對儲存，可以看成一個資料結構，提供兩個演演算法：
（1）Encode
能將一組資料\((k,v)\)編碼到一個對\(S\)象中，以可忽略的概率會出錯。
（2）Decode
可以根據\(x\)和物件\(S\)，如果\((x,y)\)在物件\(S\)中的話，則輸出對應的\(y\)，否則輸出一個隨機值。

如果是將一組點\((x,y)\)編碼到一個多項式\(f(.)\)，那麼多項式的係數就是\(S\)，可以根據\(S\)和\(s\)，得到\(f(x)\)。
當然實現不會這麼簡單～

OKVS

不經意的鍵值對儲存。對於敵手而言，輸出的\(y\)值是不可區分的。

區別

所以主要還是以OKVS為主設計協定。

Zero-Sharing

在「Practical multi-party private set intersection from symmetric-key techniques」中也用到過。

即，能讓同一個鍵對應的值的互斥或和為0

ZeroXOR

即，需要輸出的是滿足條件的鍵。

方案

不合謀

三方例子

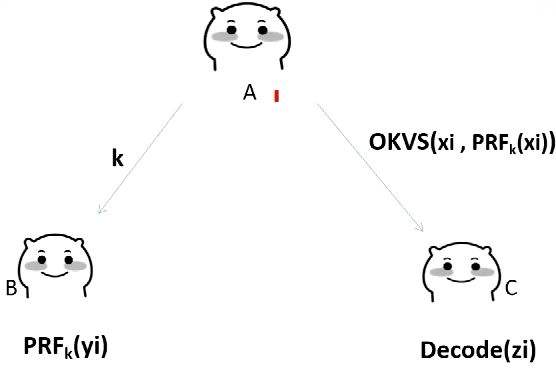
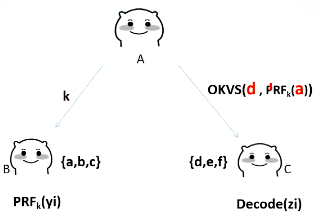
（1）A擁有金鑰\(k\)，將\(k\)傳送給\(B\)，\(B\)得到\(PRF_k(y_i)\)，\(A\)自己計算出\(PRF_k(x_i)\)。
此時三方的資料為：A有\((x_i,PRF_k(x_i))\)，B有\((y_i,PRF_k(y_i))\)，\(C\)有\((z_i)\)
（2）\(A\)將自己的資料通過OKVS編碼為物件\(OKVS(x_i,PRF_k(x_i))\)，傳送給C，如果\(z_i=x_i\)，則\(C\)獲得對應的\(PRF_k(x_i))\)，否則獲得亂數（\(C\)本身是不知道的）
（3）然後將\(A\)看作是雲，\(B\)和\(C\)將各自結果發給\(A\)去比較，如果相同，則表示\(x_i=y_i=z_i\)，屬於交集，否則不屬於交集。

注意：不能直接將\(B\)的結果傳送給\(C\)，因為\(C\)方是有物件\(OKVS(x_i,PRF_k(x_i))\)，可以無限次數查詢，可以「試出」\(B\)的\(y_i\)。
也不能直接將\(C\)的結果傳送給\(B\)，因為\(B\)方有金鑰\(k\)。【大膽一點想，如果A和B之間如果使用OPRF的話，那B就不知道金鑰了】

該方案不能防止惡意攻擊：

第一種情況：\(A\)惡意編碼錯誤

即如果\(A\)估計在OKVS時故意編碼錯誤，就會導致PSI出現錯誤！

解決辦法：

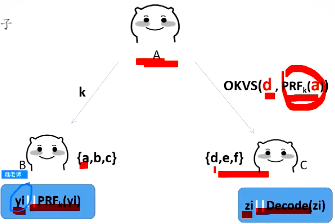
（1）\(B\)的資料\(PRF_k(y_i)\)拼接上自己的值\(y_i\)；\(C\)的資料\(Decode(z_i)\)拼接上自己的值\(z_i\)

這樣就能防止惡意的\(A\)搞破壞了！

第二種情況：在比較\(B\)和\(C\)的結果時，\(A\)惡意返回部分部分交集（1）或者惡意返回全集（2）

解決辦法：
（1）就是\(B\)和\(C\)將其結果拷貝\(\lambda\)份並串接，傳送給\(A\)，如果\(A\)搞破壞，返回部分交集，則\(B\)和\(C\)就知道有問題。【大膽一點，直接將拷貝\(\lambda\)份發過去，判斷返回結果是不是\(\lambda\)個交集，是不是也能判斷！】
（2）\(B\)和\(C\)事先協商出\(D_0,D_1,d_2\)，這樣\(A'\)和\(A^2\)肯定有交集，但又不是全集。
最後對返回結果判斷：

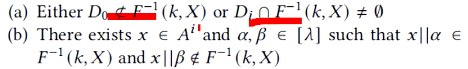
擴充套件到多方

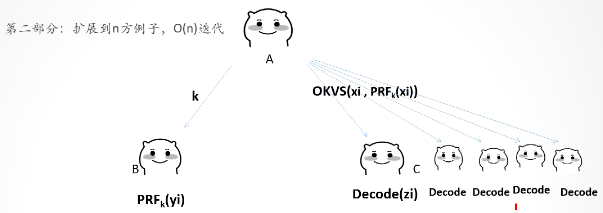
這裡在各方都有了\(PRF\)後，需要逐個迭代：\(B\)和\(C_1\)的資料在\(A\)（雲端）對比，將其結果與\(C_2\)的資料在\(A\)（雲端）對比，直到全部比較完，得到最中的交集元素，如果中間就「斷掉」了，說明該元素肯定不是所有方的交集元素。

該方案因為需要迭代逐個對比，所以複雜度很高

下面改進，降低複雜度：

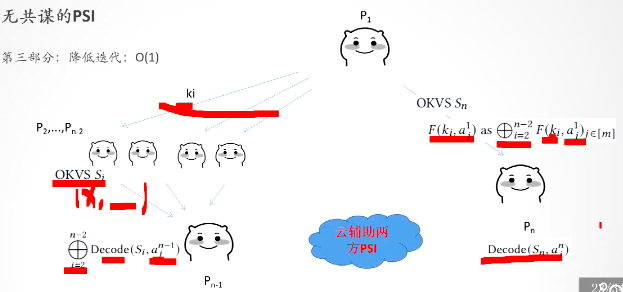
（1）\(P_1\)分別給\(P_2,...,P_{n-2}\)傳送金鑰\(k2,...,k_{n-2}\)，\(P_2,...,P_{n-2}\)分別得到\(PRF_{k_2}(y_2),...,PRF_{k_{n-2}}(y_{n-2})\)，\(P_1\)也會計算出\(PRF_{k_2}(x),...,PRF_{k_{n-2}}(x)\)。

（2）\(P_1\)將自己的資料\(PRF_{k_2}(x),...,PRF_{k_{n-2}}(x)\)互斥或得到\(PRF_{k_2}(x)\bigoplus...\bigoplus PRF_{k_{n-2}}(x)=PRF\)，然後將其進行OKVS編碼得到\(F=OKVS(x,PRF)\)，傳送給\(P_n\)
【這裡是先互斥或起來，再執行OKVS；還是先OKVS，再互斥或起來？】

（3）\(P_n\)根據自己的值\(z\)，去解碼得到\(F(z)\)，若\(x=z\)，則\(F(z)=PRF_{k_2}(x)\bigoplus...\bigoplus PRF_{k_{n-2}}(x)\)，否則，就是一個不可區分的亂數。

（4）\(P_2,...,P_{n-2}\)分別將自己的資料\(PRF_{k_2}(y_2),...,PRF_{k_{n-2}}(y_{n-2})\)進行OKVS編碼為\(F_2',...,F_{n-2}'\)，再將其互斥或\(F_2'\bigoplus ...\bigoplus F_{n-2}'=F'\)，傳送給\(P_{n-1}\)。

（5）\(P_{n-1}\)使用自己的值\(y_{n-1}\)進行解碼，得到\(F'(y_{n-1})\)，若\(y_{n-1}=y_{2}=...=y_{n-2}\)，則\(F'(y_{n-1})=PRF_{k_2}(y_2)\bigoplus...\bigoplus PRF_{k_{n-2}}(y_{n-2})\)，否則，就是一個不可區分的亂數。

（6）\(P_n\)和\(P_{n-1}\)將各自結果發給\(P_1\)去比較，如果相同，則表示\(y_{n-1}=y_{2}=...=y_{n-2}=z=x\)，屬於交集，否則不屬於交集。

以上協定，不抗合謀攻擊，並且\(P_1\)擁有全部的金鑰\(k_i\)，很不安全。

合謀

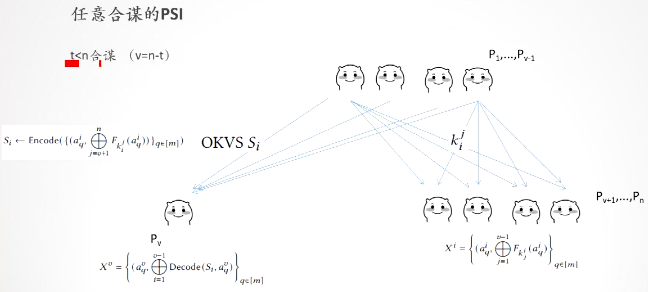
這裡共有\(n\)個參與房，\(t\)個合謀方，且滿足\(v=n-t\)
（1）\(P_1,...,P_{v-1}\)方每個都為\(P_{v+1},...,P_{n}\)生成金鑰\((k_{1,v+1},...,k_{1,n}),...,(k_{v-1,v+1},...,k_{v-1,n})\)，並行送出去。

（2）\(P_1,...,P_{v-1}\)方計算出\((PRF(x_1,k_{1,v+1}),...,PRF(x_1,k_{1,n})),...,(PRF(x_{v-1},k_{v-1,v+1}),...,PRF(x_{v-1},k_{v-1,n}))\)；\(P_{v+1},...,P_{n}\)方各自計算出\((PRF(x_{v+1},k_{1,v+1}),...,PRF(x_{v+1},k_{v-1,v+1})),...,(PRF(x_{n},k_{1,n}),...,PRF(x_{n},k_{v-1,n}))\)，然後每方將自己的資料互斥或得到\((x_{v+1},PRF(x_{v+1},k_{1,v+1})\bigoplus...\bigoplus PRF(x_{v+1},k_{v-1,v+1})),...,(x_{n},(PRF(x_{n},k_{1,n})\bigoplus...\bigoplus PRF(x_{n},k_{v-1,n}))\)，然後將所有的PRF值互斥或\(PRF(x_{v+1},k_{1,v+1})\bigoplus...\bigoplus PRF(x_{v+1},k_{v-1,v+1})\bigoplus...\bigoplus PRF(x_{n},k_{1,n})\bigoplus...\bigoplus PRF(x_{n},k_{v-1,n})\)

（3）\(P_1,...,P_{v-1}\)方先將自己的資料互斥或\((x_{1},PRF(x_1,k_{1,v+1})\bigoplus...\bigoplus PRF(x_{1},k_{1,n})),...,(x_{v-1},PRF(x_{v-1},k_{v-1,v+1})\bigoplus...\bigoplus PRF(x_{v-1},k_{v-1,n}))\)，再使用OKVS將自己互斥或後的資料編碼\(F_1,...,F_{v-1}\)，傳送給\(P_v\)方

（4）\(P_v\)方用自己的資料\(x_v\)解碼得到\(F_1(x_v),...,F_{v-1}(x_v)\)，然後再互斥或起來得到\((x_v,F_1(x_v)\bigoplus...\bigoplus F_{v-1}(x_v))\),如果\(x_v=x_1=...=x_{v-1}\)，則\((F_1(x_v)\bigoplus...\bigoplus F_{v-1}(x_v))=PRF(x_1,k_{1,v+1})\bigoplus...\bigoplus PRF(x_{1},k_{1,n})\bigoplus...\bigoplus PRF(x_{v-1},k_{v-1,v+1})\bigoplus...\bigoplus PRF(x_{v-1},k_{v-1,n})\)

（5）\(P_v\)和\(P_{v+1},...,P_{n}\)將各自結果發給\(P_1\)去比較，如果相同，則表示\(x_1=...=x_{v-1}=x_v=x_{v+1}=...x_n\)，屬於交集，否則不屬於交集。

上面需要滿足一個條件：
最後的結果互斥或起來為0。

優化

加入Zero-XOR，和Zero- Sharing技術。

各方資料為X_i=\((x_i,y_i)\)：
（1）\(P_i\)方使用Zero- Sharing，對於每一個資料（鍵）\(x_i\)，生成對應的零分享值\(s_i\)

（2）\(P_1,...,P_{n-1}\)方和\(P_n\)之間使用OPPRF：\(P_i\)方作為傳送者，將零分享值與本身值互斥或，得到\((x_i,s_i\bigoplus y_i)\)；\(P_n\)作為接收者，輸入\(x_n\)，若\((x_j,s_i\bigoplus y_i)\in X_i\),得到\(z_j=s_i\bigoplus y_i\)，否則，得到一個偽亂數

（3）\(P_n\)輸出\((x_n,z_n=\bigoplus_{j\in [n-1]}z_j)\)

總結

推薦參考

（1）知乎的解讀：Simple, Fast Malicious Multiparty Private Set Intersection
（2）B站上一位同學的組會視訊：https://www.bilibili.com/video/BV1DL411w7Zk/
（3）叮！多方隱私集合求交發來「會議邀請」