Java資料結構之AVL樹詳解
2022-06-01 14:02:05

推薦學習:《》
AVL樹的引入
搜尋二元樹有著極高的搜尋效率,但是搜尋二元樹會出現以下極端情況: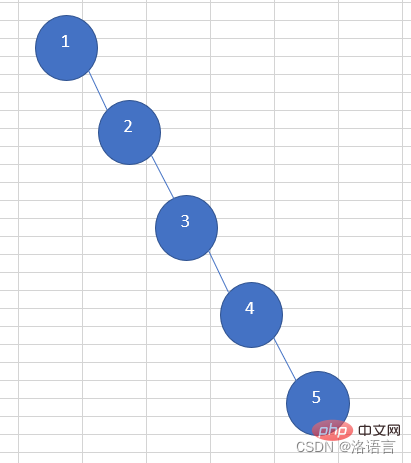
這樣的二元樹搜尋效率甚至比連結串列還低。在搜尋二元樹基礎上出現的平衡二元樹(AVL樹)就解決了這樣的問題。當平衡二元樹(AVL樹)的某個節點左右子樹高度差的絕對值大於1時,就會通過旋轉操作減小它們的高度差。
基本概念
AVL樹本質上還是一棵二元搜尋樹,它的特點是:
- 本身首先是一棵
二元搜尋樹。 - 每個結點的左右子樹的
高度之差的絕對值(平衡因子)最多為1。也就是說,AVL樹,本質上是帶了平衡功能的二叉查詢樹(二叉排序樹,二元搜尋樹)。 - 當插入一個節點或者刪除一個節點時,導致某一個節點的左右子樹高度差的絕對值大於1,這時需要通過
左旋和右旋的操作使二元樹再次達到平衡狀態。
平衡因子(balanceFactor)
- 一個結點的左子樹與右子樹的
高度之差。 - AVL樹中的任意結點的BF只可能是
-1,0和1。
基礎設計
下面是AVL樹需要的簡單方法和屬性:
public class AVLTree <E extends Comparable<E>>{
class Node{
E value;
Node left;
Node right;
int height;
public Node(){}
public Node(E value){
this.value = value;
height = 1;
left = null;
right = null;
}
public void display(){
System.out.print(this.value + " ");
}
}
Node root;
int size;
public int size(){
return size;
}
public int getHeight(Node node) {
if(node == null) return 0;
return node.height;
}
//獲取平衡因子(左右子樹的高度差,大小為1或者0是平衡的,大小大於1不平衡)
public int getBalanceFactor(){
return getBalanceFactor(root);
}
public int getBalanceFactor(Node node){
if(node == null) return 0;
return getHeight(node.left) - getHeight(node.right);
}
//判斷一個樹是否是一個平衡二元樹
public boolean isBalance(Node node){
if(node == null) return true;
int balanceFactor = Math.abs(getBalanceFactor(node.left) - getBalanceFactor(node.right));
if(balanceFactor > 1) return false;
return isBalance(node.left) && isBalance(node.right);
}
public boolean isBalance(){
return isBalance(root);
}
//中序遍歷樹
private void inPrevOrder(Node root){
if(root == null) return;
inPrevOrder(root.left);
root.display();
inPrevOrder(root.right);
}
public void inPrevOrder(){
System.out.print("中序遍歷:");
inPrevOrder(root);
}}RR(左旋)
往一個樹右子樹的右子樹上插入一個節點,導致二元樹變得不在平衡,如下圖,往平衡二元樹中插入5,導致這個樹變得不再平衡,此時需要左旋操作,如下: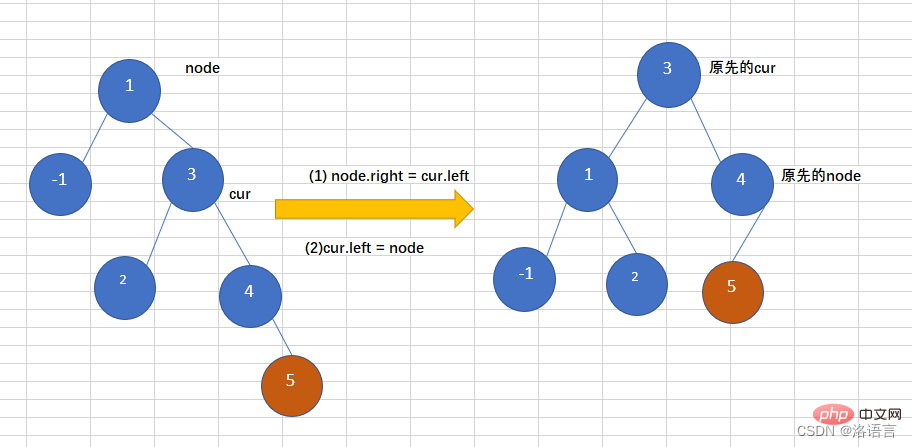
程式碼如下:
//左旋,並且返回新的根節點
public Node leftRotate(Node node){
System.out.println("leftRotate");
Node cur = node.right;
node.right = cur.left;
cur.left = node;
//跟新node和cur的高度
node.height = Math.max(getHeight(node.left),getHeight(node.right)) + 1;
cur.height = Math.max(getHeight(cur.left),getHeight(cur.right)) + 1;
return cur;
}LL(右旋)
往一個AVL樹左子樹的左子樹上插入一個節點,導致二元樹變得不在平衡,如下圖,往平衡二元樹中插入2,導致這個樹變得不再平衡,此時需要左旋操作,如下: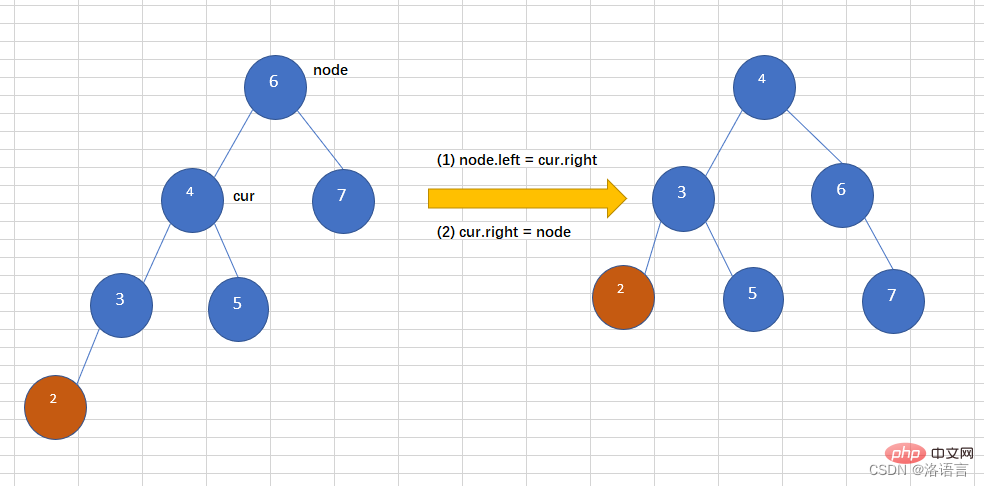
程式碼如下:
//右旋,並且返回新的根節點
public Node rightRotate(Node node){
System.out.println("rightRotate");
Node cur = node.left;
node.left = cur.right;
cur.right = node;
//跟新node和cur的高度
node.height = Math.max(getHeight(node.left),getHeight(node.right)) + 1;
cur.height = Math.max(getHeight(cur.left),getHeight(cur.right)) + 1;
return cur;
}LR(先左旋再右旋)
往AVL樹左子樹的右子樹上插入一個節點,導致該樹不再平衡,需要先對左子樹進行左旋,再對整棵樹右旋,如下圖所示,插入節點為5.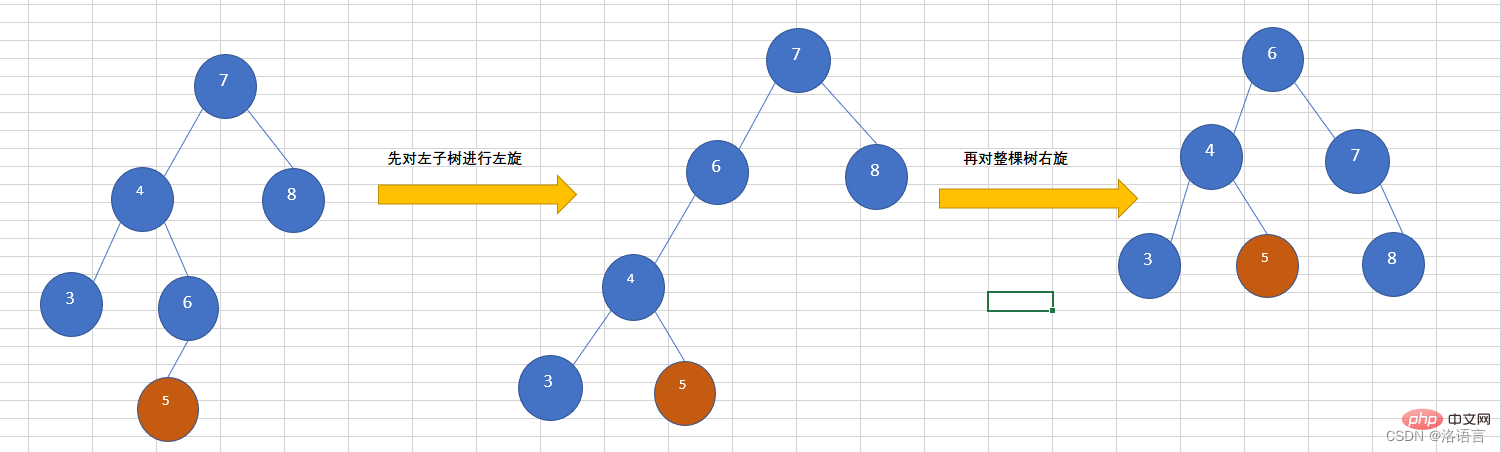
RL(先右旋再左旋)
往AVL樹右子樹的左子樹上插入一個節點,導致該樹不再平衡,需要先對右子樹進行右旋,再對整棵樹左旋,如下圖所示,插入節點為2.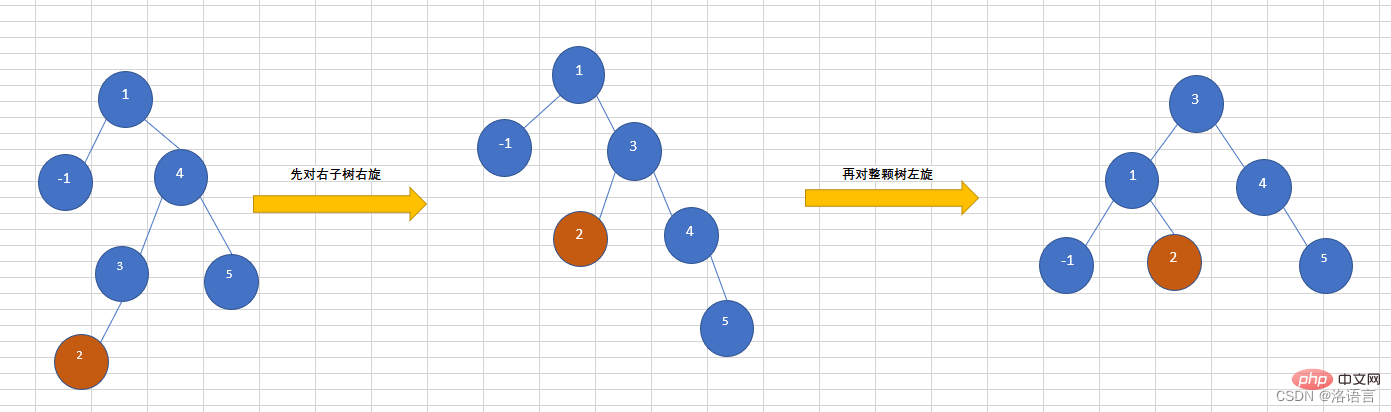
新增節點
//新增元素
public void add(E e){
root = add(root,e);
}
public Node add(Node node, E value) {
if (node == null) {
size++;
return new Node(value);
}
if (value.compareTo(node.value) > 0) {
node.right = add(node.right, value);
} else if (value.compareTo(node.value) < 0) {
node.left = add(node.left, value);
}
//跟新節點高度
node.height = Math.max(getHeight(node.left), getHeight(node.right)) + 1;
//獲取當前節點的平衡因子
int balanceFactor = getBalanceFactor(node);
//該子樹不平衡且新插入節點(導致不平衡的節點)在左子樹的左子樹上,此時需要進行右旋
if (balanceFactor > 1 && getBalanceFactor(node.left) >= 0) {
return rightRotate(node);
}
//該子樹不平衡且新插入節點(導致不平衡的節點)在右子樹子樹的右子樹上,此時需要進行左旋
else if (balanceFactor < -1 && getBalanceFactor(node.right) <= 0) {
return leftRotate(node);
}
//該子樹不平衡且新插入節點(導致不平衡的節點)在左子樹的右子樹上,此時需要先對左子樹左旋,在整個樹右旋
else if (balanceFactor > 1 && getBalanceFactor(node.left) < 0) {
node.left = leftRotate(node.left);
return rightRotate(node);
}
//balanceFactor < -1 && getBalanceFactor(node.left) > 0
//該子樹不平衡且新插入節點(導致不平衡的節點)在右子樹的左子樹上,此時需要先對右子樹右旋,再整個樹左旋
else if(balanceFactor < -1 && getBalanceFactor(node.right) > 0) {
node.right = rightRotate(node.right);
return leftRotate(node);
}
return node;
}刪除節點
//刪除節點
public E remove(E value){
root = remove(root,value);
if(root == null){
return null;
}
return root.value;
}
public Node remove(Node node, E value){
Node retNode = null;
if(node == null)
return retNode;
if(value.compareTo(node.value) > 0){
node.right = remove(node.right,value);
retNode = node;
}
else if(value.compareTo(node.value) < 0){
node.left = remove(node.left,value);
retNode = node;
}
//value.compareTo(node.value) = 0
else{
//左右節點都為空,或者左節點為空
if(node.left == null){
size--;
retNode = node.right;
}
//右節點為空
else if(node.right == null){
size--;
retNode = node.left;
}
//左右節點都不為空
else{
Node successor = new Node();
//尋找右子樹最小的節點
Node cur = node.right;
while(cur.left != null){
cur = cur.left;
}
successor.value = cur.value;
successor.right = remove(node.right,value);
successor.left = node.left;
node.left = node.right = null;
retNode = successor;
}
if(retNode == null)
return null;
//維護二元樹平衡
//跟新height
retNode.height = Math.max(getHeight(retNode.left),getHeight(retNode.right));
}
int balanceFactor = getBalanceFactor(retNode);
//該子樹不平衡且新插入節點(導致不平衡的節點)在左子樹的左子樹上,此時需要進行右旋
if (balanceFactor > 1 && getBalanceFactor(retNode.left) >= 0) {
return rightRotate(retNode);
}
//該子樹不平衡且新插入節點(導致不平衡的節點)在右子樹子樹的右子樹上,此時需要進行左旋
else if (balanceFactor < -1 && getBalanceFactor(retNode.right) <= 0) {
return leftRotate(retNode);
}
//該子樹不平衡且新插入節點(導致不平衡的節點)在左子樹的右子樹上,此時需要先對左子樹左旋,在整個樹右旋
else if (balanceFactor > 1 && getBalanceFactor(retNode.left) < 0) {
retNode.left = leftRotate(retNode.left);
return rightRotate(retNode);
}
//該子樹不平衡且新插入節點(導致不平衡的節點)在右子樹的左子樹上,此時需要先對右子樹右旋,再整個樹左旋
else if(balanceFactor < -1 && getBalanceFactor(retNode.right) > 0) {
retNode.right = rightRotate(retNode.right);
return leftRotate(retNode);
}
return retNode;
}推薦學習:《》
以上就是Java資料結構之AVL樹詳解的詳細內容,更多請關注TW511.COM其它相關文章!