技術文章 » 論文解讀(GraphDA)《Data Augmentation for Deep Graph Learning: A Survey》

論文解讀(GraphDA)《Data Augmentation for Deep Graph Learning: A Survey》

2022-06-01 06:01:11

論文資訊

論文標題：Data Augmentation for Deep Graph Learning: A Survey
論文作者：Kaize Ding, Zhe Xu, Hanghang Tong, Huan Liu
論文來源：2022, arXiv
論文地址：download 

1 介紹

　　本文主要總結圖資料增強，並對該領域的代表性方法做出歸類分析。

　　DGL 存在的兩個問題：

    • 次優圖問題：圖中包含不確定、冗餘、錯誤和缺失的節點特徵或圖結構邊。
    • 有限標籤問題：標籤資料成本高，目前大部分 DGL 方法是基於監督和半監督，擴充套件性不足。

　　圖資料增強可以分為：

　　 img

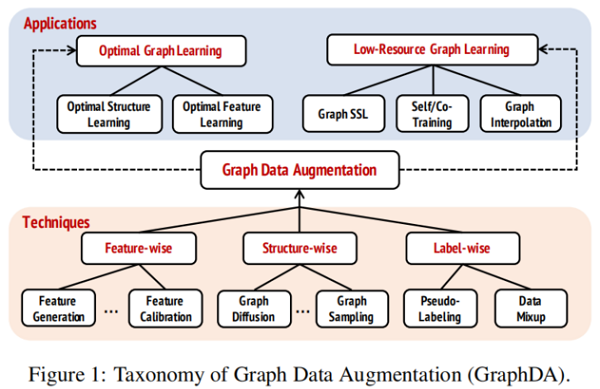
1 Techniques of Graph Data Augmentation

　　定義：$\mathcal{G}=(\mathbf{A}, \mathbf{X})$, $\mathbf{A} \in\{0,1\}^{n \times n}$, $\mathbf{X} \in \mathbb{R}^{n \times d}$, $\mathbf{y} \in \mathbb{R}^{n}$

　　GraphDA 在於找到一個對映函數 $f_{\theta}: \mathcal{G} \rightarrow \tilde{\mathcal{G}}=(\tilde{\mathbf{A}}, \tilde{\mathbf{X}})$ 來豐富圖資訊。

　　基於屬性圖的 GraphDA 可以分為:

    • feature-wise
    • structure-wise
    • label-wise

　　根據優化目標可以分為：

    • task-independent：$\underset{\theta}{\text{min }} \mathcal{L}_{a u g}\left(\left\{\mathcal{G}_{i}\right\},\left\{f_{\theta}\left(\mathcal{G}_{i}\right)\right\}\right)$
    • task-dependent：$\underset{\theta, \phi}{\text{min }} \mathcal{L}_{\text {all }}\left(\left\{\mathcal{G}_{i}\right\},\left\{f_{\theta}\left(\mathcal{G}_{i}\right)\right\}, \phi\right)$

 　　$\mathcal{L}_{a u g}(\cdot, \cdot)$, $\mathcal{L}_{a l l}(\cdot, \cdot, \cdot)$ 分別代表只對資料增強任務進行優化和聯合資料增強任務及下游任務進行優化。

1.1 Feature-wise Augmentation

　　特徵級增強策略

    • feature generation
    • feature perturbation
    • feature calibration/denoising

1.1.1 Feature Generation

　　在所有的特徵增強方法中，只有特徵生成方法改變特徵尺寸。

　　與原始特徵無關，例如，將拓撲資訊編碼成特徵，例如節點索引。之後將生成的節點特徵用於下游任務或者與原有節點進行級拼接生成新的特徵 $\{\tilde{\mathbf{X}}, \mathbf{X}\} $。（task-independent）

　　與原始特徵有關（Mixup 或者 生成模型），例如，[1] 通過生成模型來增加節點特徵，生成模型的輸入是目標節點的區域性鄰域資訊，並將生成器的優化歸納到公式中。（task-dependent）

1.1.2 Feature Perturbation

　　兩個主要的策略： feature shuffling 和 feature masking。

    • feature shuffling ：特徵矩陣 $X$ 的第 $i$ 行表示第 $i$ 個節點的節點特徵，因此對節點特徵矩陣的行進行變換等價於得到一個具有相同拓撲但排列過的節點的備選圖。由於只對節點特徵進行打亂，保留拓撲結構，會導致上述兩個分佈之間的差異，在多檢視學習中生成負樣本。(task-independent )

    • feature masking ：核心操作是將節點特徵矩陣 $X$ 中的一部分元設定為 $0$，該思想廣泛應用於對比學習。(task-independent )

　　除上述工作外，還有對抗訓練的方法來擾動節點特徵，該領域屬於圖上的對抗攻擊和對抗防禦，可以參考 [2]。　　

1.1.3 Feature Calibration/Denoising

　　由於圖資料不可避免的存在噪聲資料及感知器精度的問題，給定的節點特徵對於下游任務不是最優的。

　　此時，出現考慮對節點特徵進行較小的校準，在一定程度上存在優勢，同時也保留了大部分初始節點屬性。例如 [3] 計算特定目標函數的梯度和節點特徵矩陣，並基於計算的梯度校準節點特徵矩陣。

　　噪聲特徵的一個特例是部分特徵丟失，其對應的解決方案是特徵推斷 [4][5]。由於難以將拓撲資訊融入推斷模型種，所以在圖結構上還沒有好好的研究，相關的代表作有 GCNMF [6] 和特徵傳播 [7] 。前者用高斯混合模型表示缺失的資料；後者基於熱擴散方程將特徵從已知特徵擴散到未知特徵。

1.2 Structure-wise Augmentation

　　分為四種方法：

    • edge addition/dropping

    • node addition/dropping

    • graph diffusion

    • graph sampling

1.2.1 Edge Addition/Dropping

　　即 保留原始節點順序，對鄰接矩陣種的元進行改寫。

　　基於圖稀疏性（graph sparsification）的圖結構優化方法 [8、9]，基於圖結構整潔性（graph sanitation）的方法 [3]，以及圖取樣（graph sampling）。

　　Edge Addition/Dropping 不僅可以是任務無關的隨機丟邊，而且還可以通過將拓撲（例如，作為可學習分佈）形成到下游目標中而依賴於任務。

1.2.2 Node Addition/Dropping

　　新增節點需要做：

    • 在給定的鄰接矩陣 $A$ 中插入一行和一列；
    • 在給定的節點特徵矩陣 $X$ 中插入一行；
    • 根據特定的下游任務設定節點標籤向量 $y$；

　　節點的更改關聯圖結構和節點標籤往往更加複雜，一個典型的例子：通過在給定圖中插入超節點來改善整個圖的傳播/連通性。超節點與圖中的所有現有節點相連。它的特性是可以聚合所有現有節點的特性，也可以通過下游任務來學習。

　　為緩解不平衡的標籤分佈，GraphSMOTE[11] 插入節點來豐富少數類。從給定的圖中刪除節點是圖取樣技術的一個重要組成部分。DGL任務刪除節點的共同目標是生成擾動圖樣本[12；13；14]，並提取資訊子圖 [15]。

1.2.3 Graph Diffusion

　　圖擴散作為一種結構增強策略，圖擴散通過提供底層結構的全域性檢視來生成增廣圖。圖擴散通過計算權重將節點與它們的間接連線的鄰居節點連線，將全域性拓撲資訊注入到給定的圖鄰接中。圖擴散可以表示為：

　　　　$\mathbf{S}=\sum\limits _{k=0}^{\infty} \gamma_{k} \mathbf{T}^{k}\quad\quad\quad(2)$

　　其中：
    • $\mathbf{T} \in \mathbb{R}^{N \times N}$ 是由鄰接矩陣 $A$ 推匯出的廣義轉移矩陣；
    • $\theta$ 是決定全域性-區域性資訊比率的加權係數；
    • $\sum_{k=0}^{\infty} \gamma_{k}=1$，$\gamma_{k} \in[0,1]$；
    • $\lambda_{i} \in[0,1]$，$\lambda_{i}$ 為 $T$ 的特徵值，保證收斂；
　　圖擴散的兩個典型例子：
　　personalized PageRank (PPR) ：
　　　　$\gamma_{k}=\alpha(1-\alpha)^{k}$
　　　　$\mathbf{S}^{\mathrm{PPR}}=\alpha(\mathbf{I}-(1-\alpha) \mathbf{T})^{-1}\quad\quad\quad(4)$
　　heat kernel ：
　　　　$\gamma_{k}=e^{-t} \frac{t^{k}}{k !}$ 
　　　　$\mathbf{S}^{\text {heat }}=e^{-(\mathbf{I}-\mathbf{T}) t}\quad\quad\quad(3)$
　　其中，$\alpha$ 表示隨機遊走中的傳送概率，$t$ 為擴散時間。

1.2.4 Graph Sampling

　　圖取樣或者子圖取樣可以表示為：

　　　　$\tilde{\mathcal{G}}=\operatorname{SAMPLE}(\mathcal{G})  \quad\quad\quad(5)$

　　$\operatorname{SAMPLE}$ 可以是基於頂點的取樣[16]，基於邊的取樣 [17] ，遍歷抽樣（traversal-based sampling）[18]，其他先進的方法，如Metropolis-Hastings sampling [19]。

1.2.5 Graph Generation

　　圖生成之前與現在均是 task-independent ，代表性的工作包括 GraphRNN [20] 和 NetGAN [21]，其中，前者以自迴歸的方式建模一個圖，而後者使用 Wasserstein 生成對抗性網路目標訓練一個生成器。

　　此外，task-dependent 的圖生成也起著至關重要的作用。LDS[22]聯合學習邊離散概率分佈和節點分類器的引數。圖粗化(graph coarsening)[23] 和圖凝結(graph condensation)[24] 的問題也可以歸為這個領域，其目標是從初始大圖生成精細的圖。前者更注重尋找從原始節點到聚合節點的滿射對映，後者從頭開始生成壓縮圖。

1.3 Label-wise Augmentation

　　由於圖上缺乏人工標註的標籤，標籤級增強是 GraphDA 另一個重要研究方向。可以分為兩類：

    • pseudo labeling
    • data mixup

1.3.1 Pseudo-Labeling

　　偽標記是一種半監督學習機制，基於對未標記資料的預測，目的是獲得一個（或幾個）增強標記集。

　　在有標註資料 $D^{L}$ 上訓練 Teacher Model，將模型作用於 $D^{U}$ 來生成偽標籤 $D^{P}$ ， 最終使用混合標籤 $D^{L} \cup D^{P}$ 來訓練 Student Model。在這個意義上，標籤訊號可以通過學習到的教師模型「傳播」到未標記的資料樣本。重複迭代直到通過 Teacher Model 和 Student Model 收斂。一般而言，Pseudo-Labeling 的關鍵是通過選擇末標註資料中的哪個樣 本子集 $D^{P}$ 或在每輪中重新加權 Pseudo-Labeling 範例來降低標註噪聲。

　　深度神經網路的模型容易出錯地擬合和記憶標籤噪聲，而置信度低的偽標籤往往存在嚴重的標籤噪聲，對偽標記演演算法的成功有很大的威脅。一般來說，偽標記的關鍵是通過選擇未標記資料中的樣本子集 $D^{P}$ 或對每一輪中的偽標記範例進行重新加權來減輕標籤噪聲。

1.3.2 Data Mixup

　　除了利用未標記資料，還可以構造虛擬樣本，稱為 Mixup[25]，它直接插值訓練樣本。

　　　　$\begin{array}{l}\tilde{\mathbf{x}}=\lambda \mathbf{x}_{i}+(1-\lambda) \mathbf{x}_{j} \\\tilde{\mathbf{y}}=\lambda \mathbf{y}_{i}+(1-\lambda) \mathbf{y}_{j}\end{array} \quad\quad\quad(6)$

　　其中，$\left(\mathbf{x}_{i}, \mathbf{y}_{i}\right)$ 和 $\left(\mathbf{x}_{j}, \mathbf{x}_{j}\right)$ 是從訓練集中隨機抽取的兩個標記樣本，和 $\lambda \in[0,1]$。

　　通過這種方式，混合方法通過結合特徵向量的線性插值應該導致相關目標的線性插值來擴充套件訓練分佈。類似地，Manifold mixup[26] 對從兩個訓練樣本中學習到的中間表示進行混合。

2 Applications of Graph Data Augmentationin Deep Graph Learning

　　在本節中，將回顧並討論如何利用 GraphDA 技術來解決兩個具有代表性的DGL問題，即 optimal graph learning 和 low-resourcegraph learning。

2.1 GraphDA for Optimal Graph Learning

　　可以分為：

    • Optimal Structure Learning
    • Optimal Feature Learning

2.1.1 Optimal Structure Learning

　　Optimal Structure Learning 分為三類：

  • computing node similarities via metric learning (i.e., metric-basedmethods)

　　基於度量方法的核心思想是通過不同的度量函數估計節點相似性，代表性方法為 GAUG[27]，AdaEdge[28]，IDGL[29]。

　　GAUG[27]，它基於給定的圖拓撲訓練一個邊預測器。此外，這些度量函數可以通過下游任務的訓練進行迭代更新。例如，AdaEdge[28] 基於分類結果迭代地新增或刪除圖拓撲中的邊，並在更新的圖上訓練 GNNs 分類器，以克服過平滑問題。IDGL[29] 與 AdaEdge 有類似的想法，但基於學習到的節點嵌入更新了圖拓撲，以增強下游模型的魯棒性。

  • optimizing adjacency matrices as learnable parameters (i.e., optimization-based methods）

　　通常，圖拓撲的可微啟發式被整合到優化目標中 [30][31][32]。例如，TO-GNN[30]採用標籤平滑度，Pro-GNN[31] 採用特徵平滑度和拓撲稀疏性。除了圖拓撲約束，Gasoline[32]通過驗證節點上的評估效能（如分類損失）的反饋更新初始圖。

  • learning probabilistic distributions of graph structure (i.e., probabilistic modeling methods)

　　概率建模方法假設圖是從某些分佈中取樣的，並且這些分佈的引數是可學習的。

　　例如，LDS[22] 通過取樣獨立的引數化的伯努利分佈，並根據分類損失的反饋學習模型，對每對節點之間的邊緣進行建模。由於建模每對節點的計算成本往往很高，因此一個有效的解決方案是估計現有邊上的丟棄概率。 NeuralSparse [32] 和 PTDNet[33] 遵循這一策略。前者將邊下降概率建模為連線到目標節點的邊上的分類分佈，後者將每條現有的邊建模為伯努利分佈。他們都基於 Gumbel-Max 技巧制定了他們的具體範例。此外，Stochastic Block Model(SBM)技術有助於表示隨機圖，從而實現觀測圖。Bayesian-GCNN[34] 和GEN [35] 都制定了基於SBM的最優圖分佈。前者根據觀察到的初始圖和相應的節點標籤推斷出最優SBM；後者基於根據GNNs層的隱藏表示構造的一組 kNN 圖來推斷出最優分佈。

2.1.2 Optimal Feature Learning

　　與結構優化相比，圖特徵優化的研究還處於起步階段。

　　AirGNN[36] 旨在規範輸入節點特徵與複雜節點特徵之間的 $l_{21}$ 範數，使模型對異常特徵的耐受性更強。

　　為了處理缺失的節點特徵，一種次優初始節點特徵的特殊情況，特徵傳播 [37] 基於熱擴散方程將特徵從已知特徵擴散到未知特徵；換句話說，它用目標節點鄰域的聚合特徵替換缺失的節點特徵。GCNMF[38] 明確地將缺失的節點特徵表示為高斯混合模型，並以端到端方式學習具有下游任務的模型引數。

2.2 GraphDA for Low-Resource Graph Learning

　　GraphDA作為解決圖資料稀缺問題最有效的解決方案之一，在以下 low-resource graph learning 領域引起了廣泛關注。

2.2.1 Graph Self-Supervised Learning

　　近年來，資料增強技術被廣泛應用於圖自監督學習(SSL)中。受自動編碼器思想的啟發，圖生成建模方法對輸入圖進行資料增強，然後通過從增強圖中恢復特徵/結構資訊來學習模型。對於一個輸入圖，節點和/或邊的特徵被零或某些 token 所掩蓋。然後，目標是通過 GNNs 根據未掩蔽的資訊恢復掩蔽的特徵/結構。

　　例如，GPT-GNN[39] 提出了一個自迴歸框架來對輸入圖進行重構。給定一個節點和邊被隨機掩蔽的圖，GPT-GNN一次生成一個掩蔽節點及其邊，並優化當前迭代中生成的節點和邊的可能性。[40] 定義了 Graph Completion pretext，旨在根據目標節點的鄰居特徵和連線來恢復目標節點的掩蔽特徵。Denoising Link Reconstruction [41] 隨機刪除現有的邊以獲得擾動圖，並嘗試使用通過交叉熵損失訓練的基於成對相似度的解碼器來恢復被丟棄的連線。GraphBert [42] 利用節點特徵重建和圖結構恢復來對圖變壓器模型進行預訓練。

2.2.2 Graph Self/Co-Training

　　為了緩解資料量的問題，一個有效的解決方案是利用未標記的資料來增加稀缺的標記資料。

　　self-training [43] 基於有限標記資料訓練的 Teacher Model 將標籤歸因到未標記資料上，在訓練資料有限時已成為解決半監督節點分類問題的流行正規化。

　　在這些方法中，[44] 首先結合 GCN 和 self-training 來擴大監督訊號。CGCN [45] 通過將變分圖自動編碼器與高斯混合模型相結合來生成偽標籤。此外，M3S[46]提出了多階段的 self-training ，並利用聚類方法來消除可能不正確的偽標籤。類似的觀點也可以在 [47] 中找到。此外，最近的研究[48；49]也嘗試解耦GNN層中的轉換和傳播操作，並採用標籤傳播作為教師模型，進一步增強偽標籤的生成。

　　與 Self-training 類似，Co-training [50] 也被研究用未標記的資料來增強訓練集。它在兩個檢視上分別使用初始標記資料學習兩個分類器，並允許它們為彼此標記未標記資料，以增加訓練資料。[51]開發了一種新的多檢視半監督學習方法Co-GCN，該方法將GCN和協同訓練統一到一個框架中。

2.2.3 Graph Interpolation

　　另一種增強訓練資料的方法是使用基於插值的資料增強，如 Mixup[Zhang等人，2018]。雖然與不同於包含網格或線性序列格式的影象或自然句子不同，圖具有任意的結構和拓撲，因此使用基於插值的資料增強不適用。雖然我們可以通過插值特徵和相應的標籤來建立額外的節點，但仍然不清楚這些新節點是如何通過合成邊連線到原始節點的，從而保留整個圖的結構。同時，由於圖形資料的級聯效應，即使是簡單地從圖中刪除或新增一條邊，也會極大地改變其語意意義。

　　為了解決這些挑戰，GraphMix[Verma等人，2021]將流形混合[Verma等人，2019]應用於圖節點分類，聯合訓練全連線網路和具有共用引數的GNN，用於半監督學習中的圖節點分類。類似地，[Wangetal.，2021]也遵循流形混合方法，將嵌入空間中的節點和圖的輸入特徵進行插值作為資料增強。這些方法利用一種簡單的方法來避免處理輸入空間中的任意結構來混合一個圖對，通過混合從gnn中學習到的圖表示。GraphMixup[Wuetal.，2021]通過構建語意關係空間，並使用兩個基於上下文的邊緣預測器進行語意級特徵混合，有效地解決類不平衡節點分類任務。為了解決流形入侵的問題，[Guo和Mao，2021]提出了一種輸入級混合的方法來增加圖分類的訓練資料。圖移植[Parketal.，2022]是另一種輸入級混合圖增強方法，它可以在保留區域性結構的同時，通過用源子圖替換目標子圖來混合兩個不同結構的圖。

　　擴充訓練資料的另一種方法是使用基於內插的資料擴充，例如 Mixup，圖上的 Mixup 有一系列代表性工作[52-56]。

3 Future Directions

3.1 Data Augmentation beyond Simple Graphs

　　前面提到的大多數工作都在同質圖上開發的增強策略，其中邊緣傾向於連線具有相同屬性（如標籤、特徵）的節點。然而，異質性（即非協調性）也普遍存在於異性戀約會網路等網路中。許多現有的關於異親性圖的增強方法都側重於提高給定圖的協調性或降低/減少現有的非協調性邊]。對異親性圖的節點特徵、標籤和不存在的邊緣的增強仍未得到充分的研究。

　　此外，現有的GraphDA工作主要是為普通圖或屬性圖開發的，而針對其他型別的圖（如異構圖、超圖、多重圖）的原則增強方法仍在很大程度上未得到探索。這些複雜的圖為增強提供了更廣泛的設計空間，但也對現有的GraphDA方法的有效性提出了極大的挑戰，這對未來的探索至關重要。

3.2 Data Augmentation for Graph Imbalanced Training

　　圖的資料本身是不平衡的，它遵循冪律分佈。例如，在基準測試的Pubmed資料集上，節點被標記為三個類，但少數類只包含總節點的5.25%。這種不平衡的資料將導致下游任務特別是分類任務的次優效能，其中有效的解決方案之一是增加少數任務以緩解不平衡。對這個問題提出了一些初步的嘗試。GraphSMOTE [57] 通過混合少數節點來增加少數節點；GraphMixup[58]構建了增強少數節點的語意關係空間。然而，關於這一主題的許多挑戰仍未得到充分的探索。例如，如果少數節點的大小非常小，例如每個類的few-shot 甚至1次，那麼如何從多數類轉移知識來增加少數類是值得研究的。

3.3 Learnable and Generalizable Graph Augmentation

　　與影象不同的是，由於圖形的非歐幾里德性質和資料樣本之間的依賴性，為圖形設計有效且保留語意的資料增強技術具有挑戰性。大多數圖資料增強方法在輸入圖上採用任意增強，這可能會意外地改變圖的結構和語意模式，導致效能下降[59] 。例如，擾動一個分子圖的結構可能會產生一個具有完全不同性質的分子。因此，提出了必要的一個有原則的無噪聲圖增強函數。同時，由於不同的圖具有不同的性質，因此如何使增強方法在不同的資料集上可泛化。此外，由於不同的圖通常具有不同的圖屬性，因此在不從頭學習任意圖的情況下開發可推廣的資料增強對於提高GraphDA方法的實際使用非常重要。

4 Conclusion

　　在本文中，我們提出了一個前瞻性的結構化的圖形資料增強(GraphDA)。為了檢查GraphDA的性質，我們給出了一個正式的公式和一個分類法，以促進理解這個新出現的研究問題。具體來說，我們根據目標增強模式將GraphDA方法分為三類，即特徵增強、結構增強和標籤增強。我們進一步回顧了GraphDA方法在解決兩個以資料為中心的DGL問題（即最優圖學習和低資源圖學習）方面的應用，並討論了流行的基於GraphDA的演演算法。最後，我們概述了當前的挑戰以及未來在該領域的研究的機會。

Reference

1、Local augmentation for graph neural networks. arXiv , 2021.

2、Adversarial attack and defense on graph data: A survey. arXiv , 2018.

3、Graph sanitation with application to node classification. arXiv preprint arXiv 2021.

4、On the unreasonable effectiveness of feature propagation in learning on graphs with missing node features. arXiv, 2021.

5、Graph convolutional networks for graphs containing missing features. FGCS, 2021.

6、Graph convolutional networks for graphs containing missing features. FGCS, 2021

7、On the unreasonable effectiveness of feature propagation in learning on graphs with missingnode features. arXiv, 2021

8、Robust graph representation learning via neural sparsification. In ICML, 2020.

9、Learning to drop: Robust graph neural network via topological denoising. In WSDM, 2021.

10、Neural message passing for quantum chemistry. In ICML, 2017.

11、Graphsmote: Imbalanced node classification on graphs with graph neural networks. In WSDM, 2021.

12、Graph contrastive learning with augmentations. In NeurIPS,2020.

13、Graph contrastive learning automated. In ICML, 2021.

14、Graph contrastive learning with adaptive augmentation. In TheWebConf, 2021.

15、Graph information bottleneck for subgraph recognition. In ICLR, 2020.

16、Sub-graph contrast for scalable self-supervised graph representation learning. In ICDM, 2020.

17、Robust graph representation learning via neural sparsification. In ICML, 2020.

18、Graph contrastive coding for graph neural network pre-training. In KDD, 2020

19、Metropolis-hastings data augmentation for graph neural networks. NeurIPS, 2021.

20、Graphrnn: Generating realistic graphs with deep auto-regressive models. In ICML, 2018.

21、Netgan:Generating graphs via random walks. In ICML, 2018.

22、Learning discrete structures for graph neural networks. In ICML, 2019.

23、Graph coarsening with neural networks. In ICLR, 2021.

24、Graph condensation for graph neural networks

25、mixup: Beyond empirical risk minimization. In ICLR, 2018.

26、Manifold mixup: Better representations by interpolating hidden states. In ICML, 2019.

27、Data augmentation for graph neural networks. In AAAI, 2021.

28、Measuring and relieving the over-smoothing problem for graph neural networks from the topological view. In AAAI, 2020.

29、Iterative deep graph learning for graph neural networks: Better and robust node embeddings. NeurIPS, 2020.

30、Topology optimization based graph convolutional network. In IJCAI, 2019.

31、Graph structure learning for robust graph neural networks. In KDD, 2020.

32、 Robust graph representation learning via neural sparsification. In ICML, 2020.

33、Learning to drop: Robust graph neural network via topological denoising. In WSDM, 2021.

34、Bayesian graph convolutional neural networks for semi-supervised classification. In AAAI, 2019.

35、Graph sparsification via meta-learning. DLG@AAAI,2021.

36、Graph neural networks with adaptive residual. NeurIPS, 2021.

37、On the unreasonable effectiveness of feature propagation in learning on graphs with missing node features

38、Graph convolutional networks for graphs containing missing features. FGCS, 2021.

39、Gpt-gnn: Generative pre-training of graph neural networks. In KDD, 2020.

40、When does self-supervision help graph convolutional networks? In ICML, 2020.

41、Pre-training graph neural networks for generic structural feature extraction. arXiv, 2019.

42、Graph-bert: Only attention is needed for learning graph representations. arXiv preprint arXiv:, 2020.

43、Unsupervised word sense disambiguation rivaling supervised methods. In ACL, 1995.

44、Deeper insights into graph convolutional networks for semi-supervised learning. In AAAI, 2018.

45、Collaborative graph convolutional networks: Unsupervised learning meets semi-supervised learning. In AAAI, 2020.

46、Multi-stage self-supervised learning for graph convolutional networks on graphs with few labeled nodes. In AAAI, 2020.

47、Nrgnn: Learning a label noise-resistant graph neural network on sparsely and noisily labeled graphs. In KDD, 2021.

48、 On the equivalence of decoupled graph convolution network and label propagation. In TheWebConf, 2021.

49、Meta propagation networks for graph few-shot semi-supervised learning. In AAAI, 2022.

50、Combining labeled and unlabeled data with co-training. In COLT, 1998.

51、Co-gcn for multi-view semi-supervised learning. In AAAI, 2020.

52、Graphmix: Improved training of gnns for semi-supervised learning. In AAAI, 2021.

53、Mixup for node and graph classification. In TheWebConf, 2021.

54、Graphmixup: Improving class-imbalanced node classification on graphs by self-supervised context prediction. arXiv preprint arXiv, 2021.

55、Intrusion-free graph mixup. arXiv preprint arXiv:2110.09344, 2021.

56、Graph transplant: Node saliency-guided graph mixup with local structure preservation. In AAAI, 2022.

57、Graphsmote: Imbalanced node classification on graphs with graph neural networks. In WSDM, 2021.

58、Graphmixup: Improving class-imbalanced node classification on graphs by self-supervised context prediction. arXiv preprint arXiv, 2021.

59、Metropolis-hastings data augmentation for graph neural networks. NeurIPS, 2021.