技術文章 » LC T668筆記 & 有關二分查詢、第K小數、BFPRT演演算法

LC T668筆記 & 有關二分查詢、第K小數、BFPRT演演算法

2022-06-01 06:01:02

LC T668筆記 【涉及知識：二分查詢、第K小數、BFPRT演演算法】

【以下內容僅為本人在做題學習中的所感所想，本人水平有限目前尚處學習階段，如有錯誤及不妥之處還請各位大佬指正，請諒解，謝謝！】

 

！！！觀前提醒！！！

【本文篇幅較大，如有興趣建議分段閱讀】

 

有關二分查詢

作用：在有序集合中快速查詢目標值

適用性：

　　1. 只能查詢有序的資料集

順序儲存的資料結果就是陣列了，也就是二分查詢只能從陣列中查詢，而不能查詢鏈式儲存的資料集，比如查詢連結串列中的數，就不能用二分查詢。

　　2. 針對的是靜態有序資料集

二分查詢適合那種不經常變動的資料集合。如果經常插入、刪除的資料集，每次插入和刪除都要保證集合資料的有序，維護動態資料有序的成本很高。所以二分查詢適合從有序的不經常變動的資料集合中查詢。適合資料集合已經排好序，但是需要經常查詢的場景。

　　3. 不適合資料量太大或者太小的場景

因為二分查詢需要依賴陣列這種資料結構，而陣列要求連續的記憶體空間，其需要把所有資料全部讀入記憶體中，因此資料量太大的，對記憶體要求比較高。如果資料量只有幾十個，那麼不論是使用二分查詢還是順序遍歷，查詢效率都差不多。

 

有關二分查詢的邊界問題

「思路很簡單，細節是魔鬼」

二分的幾個常用情景：尋找一個數、尋找左側邊界、尋找右側邊界

以下是二分查詢的基本框架：

 1 public int BinarySearch(int[] nums, int target) {
 2     int left = 0, right = ...; 
 3     while(...) {
 4         int mid = left + ((right - left) >> 1);
 5         if (nums[mid] == target) {
 6             ...
 7         } else if (nums[mid] < target) {
 8             left = ...
 9         } else if (nums[mid] > target) {
10             right = ...
11         }
12     }
13     return ...;
14 }

分析二分查詢的一個技巧是：不要出現 else，而是把所有情況用 else if 寫清楚，這樣可以清楚地展現所有細節。

（一）  尋找一個數

 1 public int BinarySearch(int[] nums, int target) {
 2     int left = 0; 
 3     int right = nums.length - 1; //【1】
 4 
 5     while(left <= right) { //【2】
 6         int mid = left + ((right - left) >> 1);
 7         if(nums[mid] == target)
 8             return mid; 
 9         else if (nums[mid] < target)
10             left = mid + 1;  //【3】
11         else if (nums[mid] > target)
12             right = mid - 1;  //【4】
13     }
14     return -1;
15 }

　　1. while中的迴圈條件

迴圈條件由搜尋區間的結構確定，當找到目標值後，返回即可；

若沒找到則需考慮終止情況。此處的搜尋區間的結構是兩端閉區間。當left == right時，表示區間[left, right]，此時區間內仍有一個數值未被搜尋，若此時結束迴圈，可能錯過對目標值的匹配，因此需要繼續查詢，則終止條件應當是left > right時，此時搜尋區間為空。所以此處while中應當為「<=」。

如果要使用小於號，則在結尾加一句判斷即可。

1 return nums[left] == target ? left : -1;

　　2.  left與right的加加減減

邊界的加減也由搜尋區間的結構確定。在[left, right]中mid被檢測後，需要據mid將其劃分為兩個區間，若mid位置上的值不等於target，則不用再考慮mid。因為邊界均可取到，所以搜尋區間因改為[left, mid – 1]或[mid + 1, right]

　　3.  缺點

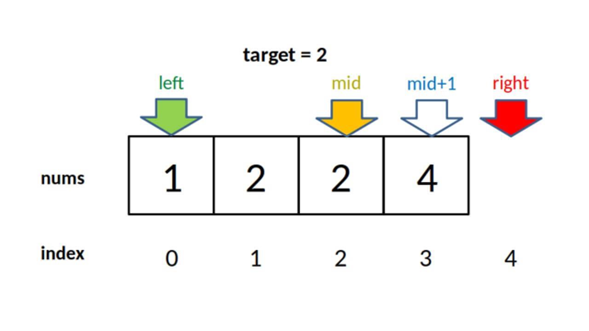
當資料中重複出現目標元素，則返回的是在重複序列中中間位置的索引，並不能得到其左側或右側邊界。如{1, 2, 2, 2, 3, 5}，target = 2，此時返回索引為2，但其邊界為[1, 3]

（二）  尋找左側邊界

 1 public int LeftBound(int[] nums, int target) {
 2     if (nums.length == 0) return -1;
 3     int left = 0;
 4     int right = nums.length; //【1】
 5     
 6     while (left < right) { //【2】
 7         int mid = left + ((left + right) >> 1);
 8         if (nums[mid] == target) {
 9             right = mid; //【3】
10         } else if (nums[mid] < target) {
11             left = mid + 1;
12         } else if (nums[mid] > target) {
13             right = mid; //【4】
14         }
15     }
16     return left;
17 }

　　1.  while中的迴圈條件

同理，此處的搜尋區間為左閉右開型，當left == right時，表示區間[left, right)，此時的區間已經為空，故可以終止。

注：這裡解釋一下為何上面用兩端閉區間，而這裡用左開後閉區間。因為這樣的寫法比較普遍，不這麼寫也可以，後文將會展示三種寫法(兩端閉，左開右閉，左閉右開)。

　　2.  left與right的加減

因為此處是左閉右開區間，在[left， right)中mid被檢測後，需要據mid將其劃分為兩個區間，[left, mid)和[mid + 1, right)。為了保證區間結構不變，所以right應變為mid，left應變為mid + 1

　　3.  有關結尾的返回值

返回值表示目標值在序列中的左側邊界，等價於小於目標值的元素個數。分析可知left的取值範圍是[0, nums.Length]，所以當left == nums.Length時，說明沒有一個元素小於target，即target在該序列中不存在，返回-1即可。（當然，最終的返回值也可以是right，因為終止條件是left == right）

1 if (left == nums.length) return -1;
2 return nums[left] == target ? left : -1;

　　4.  該演演算法的核心，即為何可以查詢左側邊界

1 if (nums[mid] == target) 
2     right = mid;

當nums[mid] == target時，因為資料有序，說明mid左側可能存在target，所以應縮小上界，不斷向左收縮。

　　5.  統一格式，將while迴圈加入等號

據原理，只需將right初值設為nums.Length – 1；right的變化改為mid – 1即可。

 1 public int LeftBound(int[] nums, int target) {
 2     int left = 0, right = nums.length - 1;
 3     while (left <= right) {
 4         int mid = left + (right - left) / 2;
 5         if (nums[mid] == target) {
 6             right = mid - 1;
 7             left = mid + 1;
 8         } else if (nums[mid] > target) {
 9             right = mid - 1;
10         } else if (nums[mid] < target) {
11             left = mid + 1;
12         }
13     }
14     if (left >= nums.length || nums[left] != target)
15         return -1;
16     return left;
17 }

（三）  尋找右邊界

 1 public int RightBound(int[] nums, int target) {
 2     if (nums.length == 0) return -1;
 3     int left = 0, right = nums.length;
 4     while (left < right) {
 5         int mid = left + ((left + right) >> 1);
 6         if (nums[mid] == target) {
 7             left = mid + 1; //【1】
 8         } else if (nums[mid] < target) {
 9             left = mid + 1;
10         } else if (nums[mid] > target) {
11             right = mid;
12         }
13     }
14     return left - 1; //【2】
15 }

　　1.  left與right的加減

因為此處是左閉右開區間，在[left， right)中mid被檢測後，需要據mid將其劃分為兩個區間，[left, mid)和[mid + 1, right) 。為了保證區間結構不變，所以right應變為mid，left應變為mid + 1

　　2.  有關最後返回值

因為對left的更新為mid + 1，結束時會產生以下結果：