正規表示式匹配問題
作者:Grey
原文連結:正規表示式匹配問題
問題連結
暴力解法
先過濾掉無效引數,比如:
在s串中,不能有.和*兩個字元,
在p串中,兩個*不能相鄰,*不能出現在p串的開始位置。
以上兩種情況下,直接返回false即可。
接下來,我們定義遞迴函數
boolean process0(char[] s, char[] p, int si, int pi)
遞迴含義是:p字串從pi出發一直到最後的字元,能否匹配出s這個字串從si出發,一直到最後的字串。
如果遞迴含義是如上定義,那麼主函數呼叫
process0(s, p, 0, 0)
即可得到結果。
接下來就是base case,
顯然,當pi到結尾位置的時候,即:無匹配串的時候,si必須也要到結尾位置才能算匹配,否則不可能匹配上
if (pi == p.length) {
return si == s.length;
}
如果沒有到結尾位置,說明:
pi還沒到結尾
如果此時si到了結尾,此時pi往後的字串必須要能消化成空串才能匹配,要讓pi及其往後消化成空串,則pi及其往後一定要是偶數長度的字串,因為如果是奇數長度的字串,無論如何都變不成空串。除了pi及其往後要符合偶數長度的字串,pi及其往後的字串一定要滿足若干個:
有效字元+'*'
的模式,這樣才能讓有效字元被*消化成空字串。
// pi還沒有到頭
if (si == s.length) {
// si已經到頭了
if (((p.length - pi) & 1) == 1) {
// pi及以後的字元必須首先是偶數個,剩餘奇數個數了,後面如何都做不到變成空串了。
return false;
}
if (pi + 1 < p.length && p[pi + 1] == '*') {
// 後面必須是 : 有效字元 + "*"的組合模式
return process0(s, p, si, pi + 2);
}
return false;
}
如果沒有滿足如上的if條件,則說明:
si也沒到頭,pi也沒到頭
此時,如果pi到了有效字元的最後一個位置,或者pi的下一個位置不是*,則p[pi]必須要獨立面對s[si],此時如果要匹配上,則首先需要滿足
s[si] == p[pi] || p[pi] == '.'
其次,s串從si+1一直到最後,也要可以被p串從pi+1到最後匹配上,邏輯如下:
// si和pi都沒到頭
if (pi == p.length - 1 || p[pi + 1] != '*') {
return (s[si] == p[pi] || p[pi] == '.') && process0(s, p, si + 1, pi + 1);
}
如果也逃過了上述的判斷,則說明:
pi 不是最後一個位置,且 p[pi+1] == '*'
那麼p[pi] 和 p[pi+1]至少可以先消解為空串,即p[pi]位置不做匹配,邏輯如下:
// p[pi]和p[pi+1]先消解為空串,讓si直接去匹配pi+2位置。
if (process0(s, p, si, pi + 2)) {
return true;
}
如果逃過了這步,說明p[pi]消解為空串這條道路行不通,所以只能讓:p[pi] 匹配 s[si],然後將p[pi+1]位置上的的*衍生出:
0個p[pi]
1個p[pi]
2個p[pi]
......
n個p[pi]
然後去匹配s串剩餘的字串。
for (int i = si; i < s.length; i++) {
if (p[pi] == s[i] || p[pi] == '.') {
// p[pi]匹配上了s[si],然後將p[pi+1]位置上的的*衍生出n個p[pi]來進行匹配
// 只要匹配上了就直接返回true
if (process0(s, p, i + 1, pi + 2)) {
return true;
}
} else {
// p[pi]未匹配上s[si],直接返回false
return false;
}
}
完整程式碼如下:
public static boolean isMatch0(String s, String p) {
if (s == null || p == null) {
return false;
}
char[] str = s.toCharArray();
char[] pStr = p.toCharArray();
return isValid(str, pStr) && process0(str, pStr, 0, 0);
}
// 首先過濾掉無效字元
private static boolean isValid(char[] str, char[] exp) {
for (char c : str) {
// str串中不能有.和*
if (c == '.' || c == '*') {
return false;
}
}
for (int i = 0; i < exp.length; i++) {
// *不能在exp的第一個位置
// 兩個*不能連在一起
if (exp[i] == '*' && (i == 0 || exp[i - 1] == '*')) {
return false;
}
}
return true;
}
private static boolean process0(char[] s, char[] p, int si, int pi) {
if (pi == p.length) {
return si == s.length;
}
// pi還沒有到頭
if (si == s.length) {
// si已經到頭了
if (((p.length - pi) & 1) == 1) {
// pi及以後的字元必須首先是偶數個,剩餘奇數個數了,後面如何都做不到變成空串了。
return false;
}
if (pi + 1 < p.length && p[pi + 1] == '*') {
// 後面必須是 : 有效字元 + "*"的組合模式
return process0(s, p, si, pi + 2);
}
return false;
}
// si和pi都沒到頭
if (pi == p.length - 1 || p[pi + 1] != '*') {
return (s[si] == p[pi] || p[pi] == '.') && process0(s, p, si + 1, pi + 1);
}
// pi 不是最後一個位置,且 p[pi+1] == '*'
// p[pi] 和 p[pi+1]至少可以先消解為空串,即p[pi]位置不做匹配
if (process0(s, p, si, pi + 2)) {
return true;
}
// 如果走到這步,p[pi]消解為空串這條道路行不通
// 所以只能讓:p[pi] 匹配 s[si]
// 然後將p[pi+1]的'*'衍生出:
// 0個p[pi]
// 1個p[pi]
// 2個p[pi]
// ...
// n個p[pi]
for (int i = si; i < s.length; i++) {
if (p[pi] == s[i] || p[pi] == '.') {
if (process0(s, p, i + 1, pi + 2)) {
return true;
}
} else {
break;
}
}
return false;
}
動態規劃解法
暴力方法中,遞迴函數的可變引數有兩個,而且是簡單引數,所以可以改成二維動態規劃,大家自行整理可能性和格子依賴關係,我自己整理了兩遍,已暈:),完整程式碼為:
public static boolean isMatch2(String s, String p) {
if (s == null || p == null) {
return false;
}
char[] str = s.toCharArray();
char[] pStr = p.toCharArray();
if (!isValid(str, pStr)) {
return false;
}
boolean[][] dp = new boolean[str.length + 1][pStr.length + 1];
// 最後一列,除了 dp[str.length][pStr.length] = true
// 其餘位置都是false
dp[str.length][pStr.length] = true;
// 最後一行
dp[str.length][pStr.length - 1] = false;
for (int i = pStr.length - 2; i >= 0; i--) {
if (((pStr.length - i) & 1) == 1) {
dp[str.length][i] = false;
} else if (i + 1 < pStr.length && pStr[i + 1] == '*') {
dp[str.length][i] = dp[str.length][i + 2];
} else {
dp[str.length][i] = false;
}
}
// 倒數第二列
for (int i = str.length - 1; i >= 0; i--) {
dp[i][pStr.length - 1] = ((str[i] == pStr[pStr.length - 1] || pStr[pStr.length - 1] == '.') && dp[i + 1][pStr.length]);
}
for (int i = str.length - 1; i>=0;i--) {
for (int j = pStr.length - 2; j >=0;j--) {
if (pStr[j+1]!='*') {
dp[i][j] = (str[i] == pStr[j] || pStr[j] == '.') && dp[i + 1][j + 1] ;
} else if (dp[i][j+2]) {
dp[i][j] = true;
} else {
for (int k = i; k < str.length; k++) {
if (pStr[j] == str[k] || pStr[j] == '.') {
if (dp[k + 1][j+2]) {
dp[i][j]= true;
break;
}
} else {
dp[i][j] = false;
break;
}
}
}
}
}
return dp[0][0];
}
// 首先過濾掉無效字元
private static boolean isValid(char[] str, char[] exp) {
for (char c : str) {
if (c == '.' || c == '*') {
return false;
}
}
for (int i = 0; i < exp.length; i++) {
if (exp[i] == '*' && (i == 0 || exp[i - 1] == '*')) {
return false;
}
}
return true;
}
列舉行為優化
通過動態規劃解法,發現了一個可以優化的地方,如果可以省略動態規劃解法中的下述for迴圈,那演演算法效率就可以高很多,
for (int k = i; k < str.length; k++) {
if (pStr[j] == str[k] || pStr[j] == '.') {
if (dp[k + 1][j+2]) {
dp[i][j]= true;
break;
}
} else {
// dp[i][j] = false;
break;
}
}
通過分析可以得到,對於一個普遍位置(i,j),如上for迴圈其實依賴關係是:
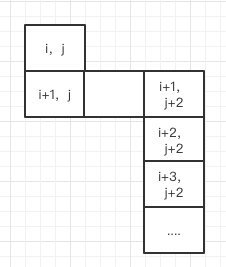
依賴(i+1,j+2),(i+2,j+2),(i+3,j+2)......
當初我們在求(i+1,j)的時候,我們依賴的位置是:
(i+2,j+2),(i+3,j+2)......
所以(i,j)位置可以由(i+1,j)和(i+1,j+2)推匯出來,如上for迴圈就簡化了,優化後的程式碼如下:
public static boolean isMatch3(String s, String p) {
if (s == null || p == null) {
return false;
}
char[] str = s.toCharArray();
char[] pStr = p.toCharArray();
if (!isValid(str, pStr)) {
return false;
}
boolean[][] dp = new boolean[str.length + 1][pStr.length + 1];
// 最後一列,除了 dp[str.length][pStr.length] = true
// 其餘位置都是false
dp[str.length][pStr.length] = true;
// 最後一行
dp[str.length][pStr.length - 1] = false;
for (int i = pStr.length - 2; i >= 0; i--) {
if (((pStr.length - i) & 1) == 1) {
dp[str.length][i] = false;
} else if (i + 1 < pStr.length && pStr[i + 1] == '*') {
dp[str.length][i] = dp[str.length][i + 2];
} else {
dp[str.length][i] = false;
}
}
// 倒數第二列
for (int i = str.length - 1; i >= 0; i--) {
dp[i][pStr.length - 1] = ((str[i] == pStr[pStr.length - 1] || pStr[pStr.length - 1] == '.') && dp[i + 1][pStr.length]);
}
for (int i = str.length - 1; i >= 0; i--) {
for (int j = pStr.length - 2; j >= 0; j--) {
if (pStr[j + 1] != '*') {
dp[i][j] = (str[i] == pStr[j] || pStr[j] == '.') && dp[i + 1][j + 1];
} else if (dp[i][j + 2]) {
dp[i][j] = true;
} else if ((pStr[j] == str[i] || pStr[j] == '.') && (dp[i + 1][j + 2] || dp[i + 1][j])) {
dp[i][j] = true;
}
}
}
return dp[0][0];
}
// 首先過濾掉無效字元
private static boolean isValid(char[] str, char[] exp) {
for (char c : str) {
if (c == '.' || c == '*') {
return false;
}
}
for (int i = 0; i < exp.length; i++) {
if (exp[i] == '*' && (i == 0 || exp[i - 1] == '*')) {
return false;
}
}
return true;
}