Scalable Multi-Party Private Set-Intersection-解讀
本文記錄閱讀該paper的筆記。
摘要

本文給出兩種MPSI協定,採用的是星型拓撲結構,即有一個leader,需要和其他參與者互動。優點是並非所有各方都必須同時線上:
(1)能抗半誠實攻擊
- 通訊複雜度與輸入資料集大小呈線性關係;
- 計算複雜度是leader方輸入資料的二次關係,其他參與者的輸入集大小呈線性關係,後面可以使用兩種hash可以消除此消耗。
(2)能抗惡意攻擊
通訊複雜度降為\(O((n^2+nm_{MAX}+nm_{MIN}logm_{MAX})k)\)bit,其中\(m_{MAX}\)和\(m_{MIN}\)分別為\(n\)個參與者的輸入最大量和輸入最小量
另外上面提到本文的半誠實方案是基於【FNP04】文章改進的,【FNP04】是最早提出MPSI的【Efficient private matching and set intersection-2013】,兩方協定是:

畫成圖表示就是:
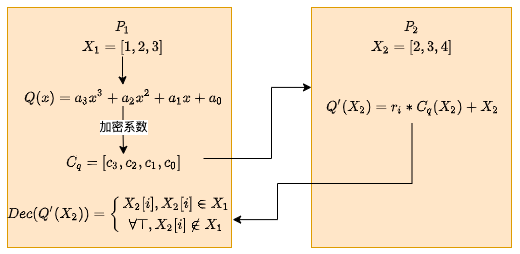
和下面介紹基於不經意多項式計算(OPE)的圖是一樣的。
介紹
MPSI

MPC的安全性通常是通過兩種對抗模型來證明的:
(1)半誠實模型
敵手遵循協定執行,但會試圖從協定中獲取更多資訊。
(2)惡意模型
敵手在多項式時間內進行攻擊

協定的優劣最根本的衡量方法就是計算消耗和通訊消耗,MPSI主要分為兩個方向:
(1)改進協定,計算任意布林/算術電路
(2)協定能計算特定的函數,例如:計算\(k\)個相同元素,模式匹配和搜尋問題,集合求交等
2PC-PSI

給出兩種方法解決PSI問題:
(1)基於不經意多項式計算(OPE)

其中,需要用同態加密(乘法和加法),但是這是兩方的PSI
(2)承諾不經意PRF計算
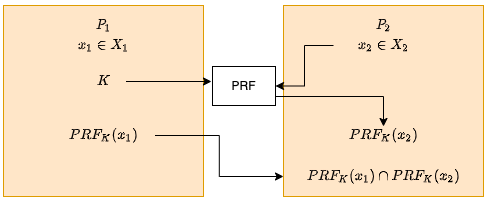
這裡只使用PRF,來「隱藏」資料,安全性和效能有待確定。

(1)【Faster private set intersection based on OT extension】【Scalable private set intersection based on OT extension】給出了基於OT和布隆布過濾器的半誠實PSI協定
(2)【Improved private set intersection against malicious adversaries】給出基於OT和布隆布過濾器的抗惡意攻擊PSI協定
(3)【Practical private set intersection protocols with linear com- plexity】【Linear-complexity private set intersection proto- cols secure in malicious model】【(if) size matters: Size-hiding private set intersection】使用了ROM(隨機預言機)模型
(4)【When private set intersection meets big data: an efficient and scalable protocol】基於OT extension和混淆不隆過濾器設計的
上面方案很少設計多方,都是兩方間的PSI
MPC-PSI

上面的這三個方案,都是多方PSI,但通訊複雜度高,對於巨量資料難以應用,效率低下。

其中【Multiparty computation from some- what homomorphic encryption】是在預處理階段使用SWHE;【MASCOT: faster malicious arithmetic secure computation with oblivious transfer】在離線階段計算,避免了不必要的線上計算量。

本文主要是設計了一個多方PSI協定,但是可以通過兩方PSI實現多方PSI,能避免通訊的二次開銷。
半誠實
採用具有加法同態性質的門限公鑰密碼方案,其中leader方輸入的資料集可以很小,並將其資料進行hash,並提供兩種hash方法:
(1)simple hashing
(2)balanced allocation hashing
使用這兩個hash,通訊量幾乎相似,計算量(2)更優,且該動起來更復雜!
惡意
預備知識
基本符號

困難問題
DLIN問題

即給出\(p,g,g^x,g^y,g^{xr},g^{ys}\),難以區分\(g^d\)和\(g^{r+s}\)。
DDH問題

即給出\(p,g,g^x,g^y\),難以區分\(g^z\)和\(g^{xy}\)。
雙線性對

公鑰加密(PKE)
IND-CPA安全


這裡的history是什麼意思?
加法同態性的公鑰加密方案

可以看到這裡的「加法同態」是:\(c_1*c_2=E(m_1+m_2)\)
門限密碼

具有加法同態性的ElGamal門限密碼方案
(1)原始ElGamal方案

(2)門限ElGamal

需有多個私鑰聯合解密,增加了一個\(F_{DecZero}\)函數,是判斷一個密文是否是0加密的。另外為了驗證私鑰的正確性,還需要ZKP.
hash函數

方案的計算量主要是在\(P_1\)計算上,至少需要\(m_1*m_i\)比較,其中\(i\in [2,n]\)。為了減少計算量,使用hash函數,各方將自己的資料(item)對映/插入到\(B\)個不同的bin中。
只有對映在相同的bin才能比較,所以比較的次數減少為\(P_1\)的輸入數量*一個bin中能裝的最大item數量。(這裡也能看出,一個bin是可以存放多個item)
simple hash

這裡使用一個hash函數,即\(h\),將\(m\)個item插入到\(B\)個bin中,其中每個bin的容量最大為\(M\),即一個bin中最多能存放\(M\)個item。
balanced allocation hash
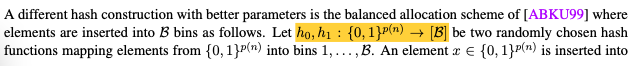

這裡使用了兩個hash函數\(h_0(),h_1()\),將\(m\)個item插入到\(B\)個bin中,其中每個bin的容量最大為\(M\)。
這裡兩個hash函數都使用了?還是選取一個使用?
半誠實模型協定
(1)這是2PC協定:

- \(P_2\)獲得私鑰\(SK\)。
- \(P_2\)計算出多項式\(Q(.)\):即\(Q(x)=(x-x2_1)...(x-x2_{m_2})\),並將係數加密傳送給\(P_1\)。
- \(P_1\)對於每一個元素\(x1_j\in X_1\),同態計算\(r_j*Q(x1_j)+x1_j\),並將結果傳送給\(P_2\)。
注意:這裡涉及到(密文明文、密文+密文、密文+明文),密文明文可以轉換為明文+明文的加密。 - \(P_2\)收到後,解密每個結果,如果結果在\(X_2\)中,則說明是在交集中,否則不在。
另外,上面是\(P_2\)擁有私鑰,\(P_2\)加密的係數,\(P_1\)只進行密文計算,\(P_2\)解密結果,並判斷。
(2)首先對2PC協定改進:

這裡說,\(P_2\)的功能不變,即產生多項式,加密係數;各方的金鑰\((PK,SK_i)\);對於\(P_1\)中的元素\(x1_j\in X_1\),同態的計算\(r_j*Q(x1_j)\);\(P_1\)的功能就是聚合多項式計算和得出交集;這裡把改造後的協定,各方的訊息的傳送表示為\(\pi_{FNP}^j,j\in (1,2)\)。
上面是改造後的兩方協定,其中\(P_2\)生成多項式,加密係數,\(P_1\)同態的計算多項式,並聯合\(P_2\)一起解密。下面完整協定中需要使用這個兩方協定構造多方協定,即\(P_1\)還是同態的計算多項式,而其它方則扮演\(P_2\)的角色,生成多項式,加密係數,並最後和\(P_1\)一起解密!
(3)完整的多方PSI協定

完整的協定,分為三部分:
第一,各方執行\(\pi_{GEN}^{SH}\),協商出一個公鑰,且不會洩露出各方的私鑰。(意思就是各方都有一個私鑰,這滿足前面提到的門限加密)
第二,\(P_1\)使用改進後的2PC協定和各方互動得到係數密文。(也就是加密的Q(xi_j)\(係數)
第三,各方執行\)\pi _{DecZsro}^{SH}\(,\)P_1$得到所有的交集。
下面詳細看:
輸入:各方\(P_i\)的輸入集合\(X_i=(x1_1,...,x1_{m_1})\),集合大小為\(m_1\),其中\(i\in [1,n]\)
第一:各方一起執行\(\pi_{GEN}^{SH}\),得到一個公鑰\(PK\)和每人一個私鑰\((SK_1,...,SK_n)\)
第二:\(P_1\)和各方(即\(P_2,...,P_n\))逐一執行協定\((\pi _{FNP}^{1},\pi _{FNP}^{2})\),得到結果密文\((ci_1,...,ci_{m_i})\),其中\(i\in [2,n]\)(這裡如果是係數的話,不是應該有\(m_i+1\)個麼?)
意思就是,各方\(P_i\)生成多項式\(Q(.)\),然後加密係數,將其發給\(P_1\),\(P_1\)再將所有的加密係數「整合」為一個加密的\(Q_1()\),並對於每一個元素同態的計算\(r_j*Q_1(x1_j)\)。
第三,就是計算交集。
從各方收到結果密文後,\(P_1\)計算:
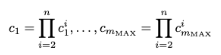
其中\(m_{MAX}=max(m_2,...,m_n)\),畫個圖理解一下:
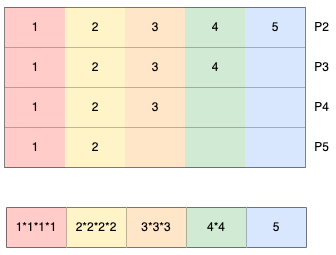
這裡相當於\(P_1\)計算\(Q_1=Q_2()+...+Q_n()\)(別忘記了,這裡使用的加法同態是:\(c_1*c_2=E(m_1+m_2)\))
這裡的意思是,各方計算出\(Q_i()\),然後加密係數,傳送給\(P_1\),\(P_1\)再將這些密文係數對應相加得到\(Q_1()\),再將\(P_1\)的集合元素代入,計算出\(m_1\)個結果,再將其解密,根據是否為0判斷是交集!(和之前的協定相反,這裡的加密是在各方進行,解密是在\(P_1\)執行,且需要聯合各方(多個私鑰))。
分析一下同態計算:
將多個加密的係數「整合」在一起,其實是想\(Q_2()+Q_3+...+Q_n()\),根據加法同態性,需要將密文係數相乘達到「相加」的效果。那麼現在得到了\(Q_1()\)的密文係數,代入\(P_1\)的集合元素(明文),計算\(r_i*Q_1(x1_j)\),這裡面涉及到密文明文(係數乘元素),密文+密文(計算後的各項相加),明文密文(亂數乘最終結果)。
靈魂疑問:僅「加法」同態能實現麼?
通訊和計算複雜度

協定消耗主要是在門限加/解密(同態計算)和2PC協定。
(1)對於改進的2PC協定,通訊消耗是在要傳輸\(m_2+1\)個密文;對於\(P_1\)的計算量又是巨大的,需要為每個元素都要執行\(O(m_2)\)的指數運算,對於全部的元素\(m_1\),則總共需要\(O(m_1.m_2)\)的指數元素。
(2)為了減少計算量,會使用hash函數,給出兩種:simple hashing和balanced allocation hash
使用simple hash

在該方案中,各方使用\(h\)hash函數,以\(P_2\)為例,每個bin中最多儲存\(M\)個數,可以看成一個\(M\)次的多項式的根儲存在一個bin中,如果不夠\(M\)個,則可以填充0,結果就是有\(B\)個bin,即\(B\)個次數為\(M\)的多項式,\(m_2\)個非零根。
對於\(P_1\)來說,將每一個元素\(x1_j\)插入到一個bin中,然後計算對應的bin,就相當於計算多項式。
對於通訊複雜度,需要傳送\(B.M_i=O(m_i)\)個密文,其中\(M_i\)是用於分配\(P_1\)輸入的bin大小在與\(P_i\)方互動時。
對於計算複雜度,\(P_1\)對於每一方需要\(O(M_i)\)的指數運算,總共需要執行\(O(m_1*\sum_{i}M_i)\)的指數元素。
這裡存在一個疑問:\(M_i\)和\(m_i\)有什麼區別?\(m_i\)是\(P_i\)方的集合大小,\(M_i\)是\(P_1\)與\(P_i\)互動時,\(P_1\)的輸入對應的一個bin的容量。
使用balanced allocation hash

這裡使用兩個hash函數,bin的個數\(B\)和最大容量\(M\)和simple hash不一樣。
以\(P_2\)為例,將其\(m_2\)個元素插入到\(B\)個bin中的一個,其中每一個bin的最大容量為\(M\),這裡是將每一個bin看作是一個\(M\)次的多項式。形成多項式\(Q_1(),...,Q_B()\),\(Q_i()\)的根在第\(i\)個bin中儲存。
當\(P_1\)收到所有的加密多項式,同態計算出\(r0^j*Q_{h_1}(x1_j)\)和\(r1^j*Q_{h_1}(x1_j)\),將其相乘,解密後為0,則表明\(x1_j\)為交集元素。