技術文章 » 論文解讀（GCC）《GCC: Graph Contrastive Coding for Graph Neural Network Pre-Training》

論文解讀（GCC）《GCC: Graph Contrastive Coding for Graph Neural Network Pre-Training》

2022-05-30 12:07:17

論文資訊

論文標題：GCC: Graph Contrastive Coding for Graph Neural Network Pre-Training
論文作者：Jiezhong Qiu, Qibin Chen, Yuxiao Dong, Jing Zhang, Hongxia Yang, Ming Ding, Kuansan Wang, Jie Tang
論文來源：2020, KDD
論文地址：download
論文程式碼：download

1 Introduction

　　本文的預訓練任務：子圖範例判別（subgraph instance discrimination）。對於每個頂點，將其 r-ego networks 作為取樣子圖範例，GCC 的目的是區分從特定頂點取樣的子圖和從其他頂點取樣的子圖。

2 Related work

　　接下來介紹幾種頂點相似性：

Neighborhood similarity

　　有邊相連的節點被認為是相似的，鄰居相似性方法有：

    • Jaccard similarity (counting common neighbors)
    • RWR similarity [36]
    • SimRank [21]

Structural similarity

　　結構相似性的基本假設是，具有相似區域性結構的頂點被認為是相似的。

　　第一種基於領域知識：

    • vertex degree　　
    • structural diversity [51]　　
    • structural hole [7]　　
    • k-core [2]　　
    • motif [5, 32]　　

　　第二種基於譜圖理論。

Attribute similarity

　　利用圖資料屬性，進一步度量相似性。

3 Method

　　Figure 2 展示了GCC的 pre-training 和 fine-tuning 階段的概述。

　　

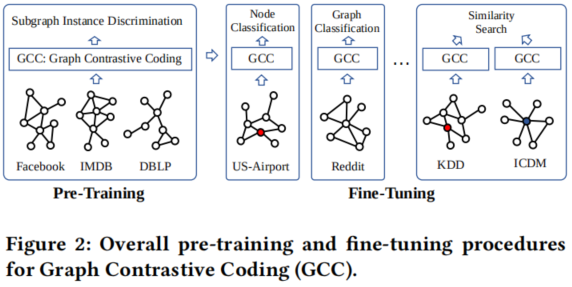
3.1 The GNN Pre-Training Problem

　　GNN 的訓練目標是學習一個函數 $f$，將節點對映到一個低維的特徵向量，具有以下兩個屬性：

    • 首先，structural similarity，具有相似拓撲結構的節點在向量空間種對映相近；
    • 其次，transferability，對於圖中不可見的節點任然可以預測；

3.2 GCC Pre-Training

　　pre-training task 將其他子圖範例視為自己的不同類，並學習區分這些範例。

　　從字典查詢的角度來看，給定一個 query $\boldsymbol{q}$ 和一個包含 $K+1$ 個 keys $\left\{\boldsymbol{k}_{0}, \cdots, \boldsymbol{k}_{K}\right\}$ 的字典，對比學習查詢 $\boldsymbol{q}$ 在字典中匹配的鍵  $\boldsymbol{k}_{+}$ 。本文采用了 InfoNCE ：

　　　　${\large \mathcal{L}=-\log \frac{\exp \left(\boldsymbol{q}^{\top} \boldsymbol{k}_{+} / \tau\right)}{\sum\limits_{i=0}^{K} \exp \left(\boldsymbol{q}^{\top} \boldsymbol{k}_{i} / \tau\right)}}  $

　　其中，$\tau$ 為溫度超引數。$f_{q}$ 和 $f_{k}$ 是兩個 GNN encoder ，將 query $x^{q}$ 和 keys $x^{k}$ 編碼為 $d$ 維表示，用 $\boldsymbol{q}=f_{q}\left(x^{q}\right)$ 和 $\boldsymbol{k}=f_{k}\left(x^{k}\right)$ 表示。

Q1: Design (subgraph) instances in graphs

　　Definition 3.1. A r-ego network. Let  $G=(V, E)$  be a graph, where  $V$  denotes the set of vertices and  $E \subseteq V \times V$  denotes the set of edges . For a vertex  $v$ , its  r -neighbors are defined as  $S_{v}=\{u  :  d(u, v) \leq r\}$  where  $d(u, v)$  is the shortest path distance between  $u$  and  $v$  in the graph  $G$ . The  r -ego network of vertex  $v$ , denoted by  $G_{v}$ , is the sub-graph induced by  $S_{v}$ .

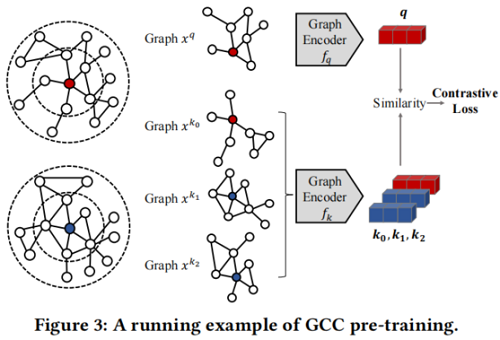
　　Figure 3 的左面板顯示了兩個 2-ego networks 的例子。GCC將其他 r-ego network 視為不同的類，並鼓勵模型將相似的範例與不同的範例區分開來。
　　

Q2: Define (dis)similar instances

　　在GCC中，將相同節點的 r-ego 網路作為一個相似的範例對，負樣本通過圖抽樣生成。

　　GCC 的圖取樣遵循以下三個步驟：

    • Random walk with restart。從頂點 $v$ 開始在 $G$ 上隨機遊走。該遊走以與邊權值成正比的概率迭代地移動到它的鄰域。此外，在每一步中，遊走有一定概率返回到起始頂點 $v$。
    • Subgraph induction。根據上述遊走路徑獲得頂點 $v$ 的頂點子集，用 $\widetilde{S}_{v}$ 表示。然後，用 $\widetilde{S}_{v}$ 生成誘導子圖 $\widetilde{G}_{v}$ (ISRW 方法)。
    • Anonymization。將上述取樣的圖節點重新打上標記 $\left\{1,2, \cdots,\left|\widetilde{S}_{v}\right|\right\}$ ，即將取樣圖的 $\widetilde{G}_{v}$ 匿名化。

　　重複上述過程兩次來建立兩個資料增強，形成一個正範例對 $\left(x^{q}, x^{k_{+}}\right)$。如果兩個子圖從不同的 r-ego networks 中獲得，將它們視為一個具有 $k \neq k_{+}$ 的不同範例對 $\left(x^{q}, x^{k}\right)$。

　　回想一下，我們關注於結構表示預訓練，而大多數GNN模型需要頂點特徵/屬性作為輸入。為了彌合差距，我們利用每個取樣子圖的圖結構來初始化頂點特徵。具體來說，我們將廣義位置嵌入定義如下：

　　Definition 3.2. Generalized positional embedding.For each subgraph, its generalized positional embedding is defined to be the top eigenvectors of its normalized graph Laplacian. Formally, suppose one subgraph has adjacency matrix  $A$  and degree matrix  $D$ , we conduct eigen-decomposition on its normalized graph Laplacian s.t.  $\boldsymbol{I}-\boldsymbol{D}^{-1 / 2} \boldsymbol{A} D^{-1 / 2}=\boldsymbol{U} \boldsymbol{\Lambda} \boldsymbol{U}^{\top}$ , where the top eigenvectors in  $\boldsymbol{U}$  are defined as generalized positional embedding.

　　FACT. The Laplacian of path graph has eigenvectors:  $\boldsymbol{u}_{k}(i)=   \cos (\pi k i / n-\pi k / 2 n)$ , for  $1 \leq k \leq n, 1 \leq i \leq n$ . Here  $n$  is the number of vertices in the path graph, and  $\boldsymbol{u}_{k}(i)$  is the entry at  $i-th$ row and  $k-th$ column of  $\boldsymbol{U}$ , i.e.,  $\boldsymbol{U}=\left[\begin{array}{lll}\boldsymbol{u}_{1} & \cdots & \boldsymbol{u}_{n}\end{array}\right]$ .

　　以上事實表明，在序列模型中的位置嵌入可以看作是路徑圖的拉普拉斯特徵向量。這激發了我們將位置嵌入從路徑圖推廣到任意圖。使用標準化圖拉普拉斯圖而非非標準化圖的原因是路徑圖是一個正則圖（即常度），而現實世界的圖通常是不規則的，有傾斜的度分佈。除了廣義位置嵌入外，我們還新增了頂點度[59]的獨熱編碼和自我頂點的二進位制指標作為頂點特徵。在由圖編碼器編碼後，最終的 $d$ 維輸出向量然後用它們的 L2-Norm 進行歸一化。

　　MoCo 旨在增加字典的大小，而不需要額外的反向傳播成本。具體地說，MoCo 維護了來自之前小批次的樣本佇列。在優化過程中，MoCo 只通過反向傳播來更新 $f_{q}$ 的引數(用 $\theta_{q}$ 表示)。$f_{k}$ 的引數(用 $\theta_{k}$ 表示)沒有通過梯度下降進行更新。[17]等人為 $\theta_{k}$ 提出了一個基於動量的更新規則。形式上，MoCo 由 $\theta_{k} \leftarrow m \theta_{k}+(1-m) \theta_{q}$ 更新 $\theta_{k}$，其中 $m \in[0,1)$ 是一個動量超引數。上述動量更新規則在 $\theta_{q}$ 中逐步將更新傳播到 $\theta_{k}$，使 $\theta_{k}$ 平穩、一致地發展。綜上所述，MoCo以犧牲字典一致性為代價實現了更大的字典規模，即字典中的金鑰表示由一個平滑變化的金鑰編碼器進行編碼。

3.3 GCC Fine-Tuning

　　圖學習中的下游任務通常可分為圖級和節點級兩類，其目標分別是預測圖級或節點的標籤。對於圖級任務，輸入圖本身可以由 GCC 進行編碼，以實現表示。對於節點級的任務，節點表示可以通過編碼其 r-ego 網路(或從其 r-ego 網路增強的子圖)來定義。

Freezing vs. full fine-tuning

　　GCC為下游任務提供了兩種微調策略——freezing mode 和 fine-tuning mode。

    • 在 freezing mode 下，凍結預先訓練的圖編碼器 $f_{q}$ 的引數，並將其作為靜態特徵提取器，然後在提取的特徵之上訓練針對特定下游任務的分類器。
    • 在 fine-tuning mode 下，將用預先訓練好的引數初始化的圖編碼器 $f_{q}$ 與分類器一起對下游任務進行端到端訓練。
GCC as a local algorithm

　　GCC作為一種圖演演算法，屬於區域性演演算法類別，由於GCC通過基於隨機遊走（大規模）網路的圖取樣方法來探索區域性結構，因此GCC只涉及對輸入（大規模）網路的區域性探索。這種特性使GCC能夠擴充套件到大規模的圖學習任務，並對分散式計算設定非常友好。

4 Experiments

資料集

 　　

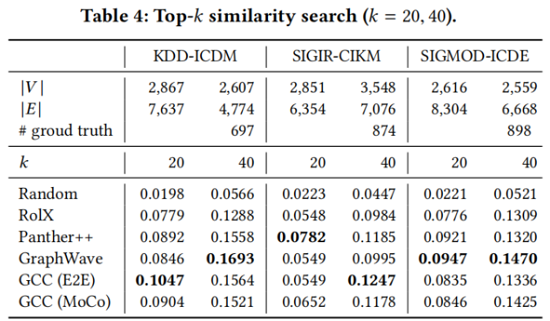
節點分類

　　

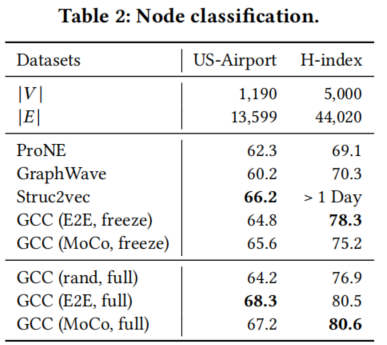
圖分類

　　

Top-k Similarity Search

　　

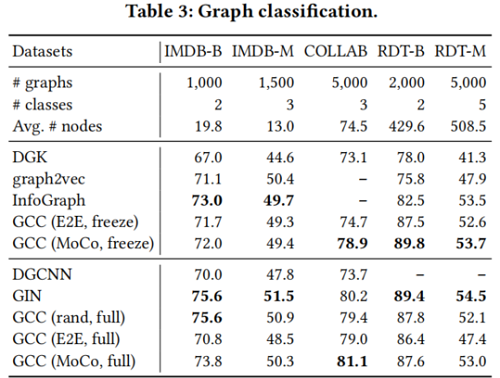
5 Conclusion

　　在本研究中，我們研究了圖神經網路的預訓練，目的是表徵和轉移社會和資訊網路中的結構表徵。我們提出了圖對比編碼(GCC)，這是一個基於圖的對比學習框架，用於從多個圖資料集。預先訓練的圖神經網路在10個圖資料集上的三個圖學習任務中實現了與監督訓練的從頭開始的競爭效能。在未來，我們計劃在更多樣化的圖形資料集上基準測試更多的圖學習任務，比如蛋白質-蛋白質關聯網路。