深度學習與CV教學(4) | 神經網路與反向傳播

作者：韓信子@ShowMeAI
教學地址：http://www.showmeai.tech/tutorials/37
本文地址：http://www.showmeai.tech/article-detail/263
宣告：版權所有，轉載請聯絡平臺與作者並註明出處
收藏ShowMeAI檢視更多精彩內容

本系列為 斯坦福CS231n 《深度學習與計算機視覺(Deep Learning for Computer Vision)》的全套學習筆記，對應的課程視訊可以在這裡檢視。更多資料獲取方式見文末。

引言

在上一篇 深度學習與CV教學(3) | 損失函數與最佳化 內容中，我們給大家介紹了線性模型的損失函數構建與梯度下降等優化演演算法，【本篇內容】ShowMeAI給大家切入到神經網路，講解神經網路計算圖與反向傳播以及神經網路結構等相關知識。

本篇重點

神經網路計算圖
反向傳播
神經網路結構

1.反向傳播演演算法

神經網路的訓練，應用到的梯度下降等方法，需要計算損失函數的梯度，而其中最核心的知識之一是反向傳播，它是利用數學中鏈式法則遞迴求解複雜函數梯度的方法。而像tensorflow、pytorch等主流AI工具庫最核心的智慧之處也是能夠自動微分，在本節內容中ShowMeAI就結合cs231n的第4講內容展開講解一下神經網路的計算圖和反向傳播。

關於神經網路反向傳播的解釋也可以參考ShowMeAI的 深度學習教學 | 吳恩達專項課程 · 全套筆記解讀 中的文章 神經網路基礎、淺層神經網路、深層神經網路 裡對於不同深度的網路前向計算和反向傳播的講解

1.1 標量形式反向傳播

1) 引例

我們來看一個簡單的例子，函數為 $f(x,y,z) = (x + y) z$。初值 $x = -2$，$y = 5$，$z = -4$。這是一個可以直接微分的表示式，但是我們使用一種有助於直觀理解反向傳播的方法來輔助理解。

下圖是整個計算的線路圖，綠字部分是函數值，紅字是梯度。（梯度是一個向量，但通常將對 $x$ 的偏導數稱為 $x$ 上的梯度。）

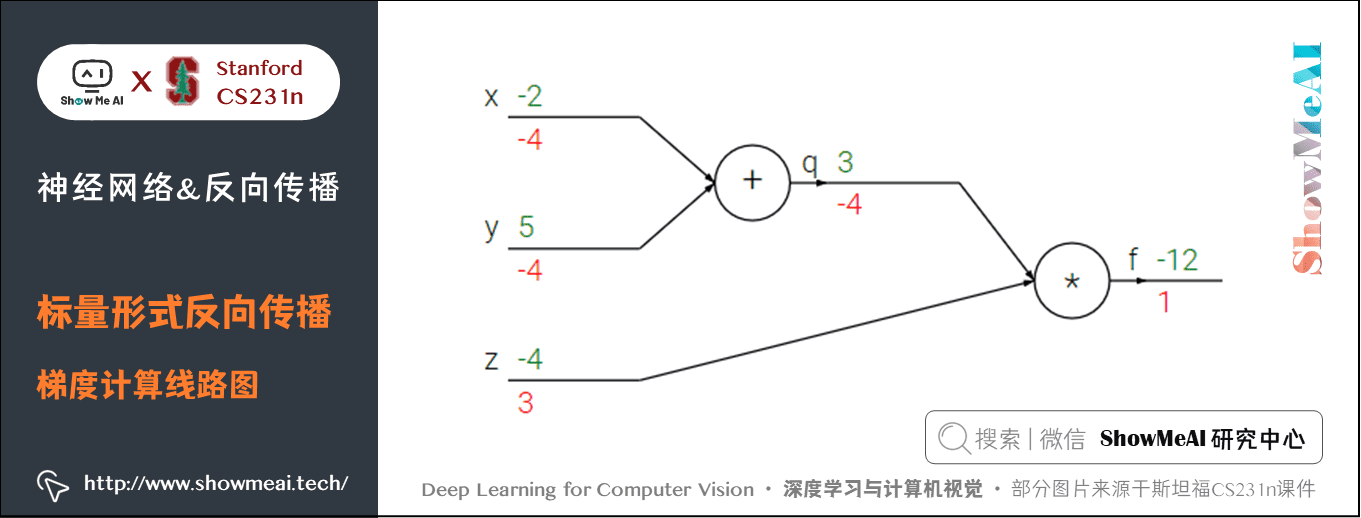
上述公式可以分為2部分， $q = x + y$ 和 $f = q z$。它們都很簡單可以直接寫出梯度表示式：

$f$ 是 $q$ 和 $z$ 的乘積，所以 $\frac{\partial f}{\partial q} = z=-4$，$\frac{\partial f}{\partial z} = q=3$
$q$ 是 $x$ 和 $y$ 相加，所以 $\frac{\partial q}{\partial x} = 1$，$\frac{\partial q}{\partial y} = 1$

我們對 $q$ 上的梯度不關心（ $\frac{\partial f}{\partial q}$ 沒有用處）。我們關心 $f$ 對於 $x,y,z$ 的梯度。鏈式法則告訴我們可以用「乘法」將這些梯度表示式連結起來，比如

\[\frac{\partial f}{\partial x} = \frac{\partial f}{\partial q} \frac{\partial q}{\partial x} =-4 \]

同理， $\frac{\partial f}{\partial y} =-4$，還有一點是 $\frac{\partial f}{\partial f}=1$

前向傳播從輸入計算到輸出（綠色），反向傳播從尾部開始，根據鏈式法則遞迴地向前計算梯度（顯示為紅色），一直到網路的輸入端。可以認為，梯度是從計算鏈路中迴流。

上述計算的參考 python 實現程式碼如下：

# 設定輸入值
x = -2; y = 5; z = -4

# 進行前向傳播
q = x + y # q 是 3
f = q * z # f 是 -12

# 進行反向傳播:
# 首先回傳到 f = q * z
dfdz = q # df/dz = q, 所以關於z的梯度是3
dfdq = z # df/dq = z, 所以關於q的梯度是-4
# 現在回傳到q = x + y
dfdx = 1.0 * dfdq # dq/dx = 1. 這裡的乘法是因為鏈式法則。所以df/dx是-4
dfdy = 1.0 * dfdq # dq/dy = 1.所以df/dy是-4

'''一般可以省略df'''

2) 直觀理解反向傳播

反向傳播是一個優美的區域性過程。

以下圖為例，在整個計算線路圖中，會給每個門單元（也就是 $f$ 結點）一些輸入值 $x$ , $y$ 並立即計算這個門單元的輸出值 $z$ ，和當前節點輸出值關於輸入值的區域性梯度（local gradient） $\frac{\partial z}{\partial x}$ 和 $\frac{\partial z}{\partial y}$ 。

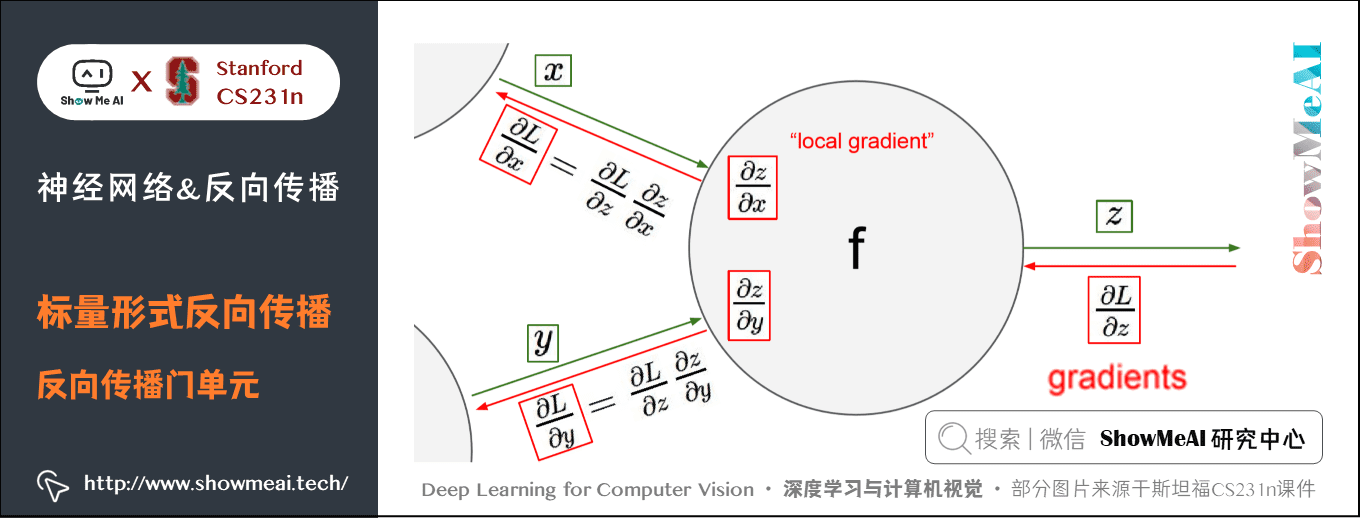
門單元的這兩個計算在前向傳播中是完全獨立的，它無需知道計算線路中的其他單元的計算細節。但在反向傳播的過程中，門單元將獲得整個網路的最終輸出值在自己的輸出值上的梯度 $\frac{\partial L}{\partial z}$ 。

根據鏈式法則，整個網路的輸出對該門單元的每個輸入值的梯度，要用回傳梯度乘以它的輸出對輸入的區域性梯度，得到 $\frac{\partial L}{\partial x}$ 和 $\frac{\partial L}{\partial y}$ 。這兩個值又可以作為前面門單元的回傳梯度。

因此，反向傳播可以看做是門單元之間在通過梯度訊號相互通訊，只要讓它們的輸入沿著梯度方向變化，無論它們自己的輸出值在何種程度上升或降低，都是為了讓整個網路的輸出值更高。

比如引例中 $x,y$ 梯度都是 $-4$，所以讓 $x,y$ 減小後，$q$ 的值雖然也會減小，但最終的輸出值 $f$ 會增大（當然損失函數要的是最小）。

3) 加法門、乘法門和max門

引例中用到了兩種門單元：加法和乘法。

加法求偏導： $f(x,y) = x + y \rightarrow \frac{\partial f}{\partial x} = 1 \frac{\partial f}{\partial y} = 1$
乘法求偏導： $f(x,y) = x y \rightarrow \frac{\partial f}{\partial x} = y \frac{\partial f}{\partial y} = x$

除此之外，常用的操作還包括取最大值：

\[\begin{aligned} f(x,y) &= \max(x, y) \\ \rightarrow \frac{\partial f}{\partial x} &= \mathbb{1}(x \ge y)\\ \frac{\partial f}{\partial y} &\mathbb{1}(y \ge x) \end{aligned} \]

上式含義為：若該變數比另一個變數大，那麼梯度是 $1$，反之為 $0$。

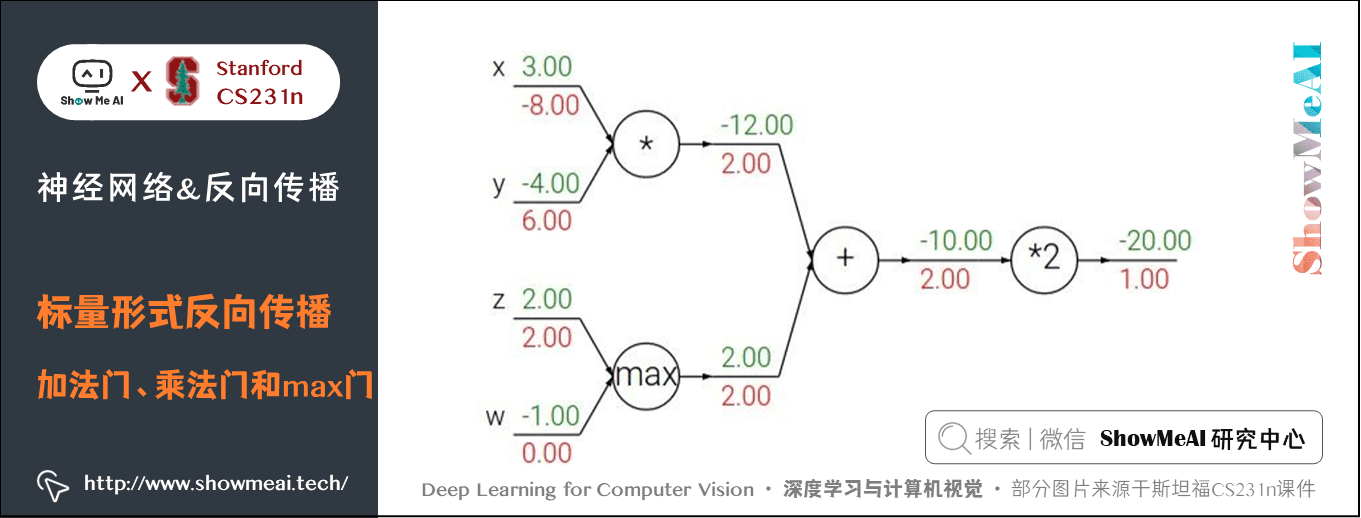
加法門單元是梯度分配器，輸入的梯度都等於輸出的梯度，這一行為與輸入值在前向傳播時的值無關；
乘法門單元是梯度轉換器，輸入的梯度等於輸出梯度乘以另一個輸入的值，或者乘以倍數 $a$（$ax$ 的形式乘法門單元）；max 門單元是梯度路由器，輸入值大的梯度等於輸出梯度，小的為 $0$。

乘法門單元的區域性梯度就是輸入值，但是是相互交換之後的，然後根據鏈式法則乘以輸出值的梯度。基於此，如果乘法門單元的其中一個輸入非常小，而另一個輸入非常大，那麼乘法門會把大的梯度分配給小的輸入，把小的梯度分配給大的輸入。

以我們之前講到的線性分類器為例，權重和輸入進行點積 $w^Tx_i$ ，這說明輸入資料的大小對於權重梯度的大小有影響。具體的，如在計算過程中對所有輸入資料樣本 $x_i$ 乘以 100，那麼權重的梯度將會增大 100 倍，這樣就必須降低學習率來彌補。

也說明了資料預處理有很重要的作用，它即使只是有微小變化，也會產生巨大影響。

對於梯度在計算線路中是如何流動的有一個直觀的理解，可以幫助偵錯神經網路。

4) 複雜範例

我們來看一個複雜一點的例子：

\[f(w,x) = \frac{1}{1+e^{-(w_0x_0 + w_1x_1 + w_2)}} \]

這個表示式需要使用新的門單元：

\[\begin{aligned} f(x) &= \frac{1}{x} \\ \rightarrow \frac{df}{dx} &=- \frac{1}{x^2}\ f_c(x) = c + x \\ \rightarrow \frac{df}{dx} &= 1 \ f(x) = e^x \\ \rightarrow \frac{df}{dx} &= e^x \ f_a(x) = ax \\ \rightarrow \frac{df}{dx} &= a \end{aligned} \]

計算過程如下：

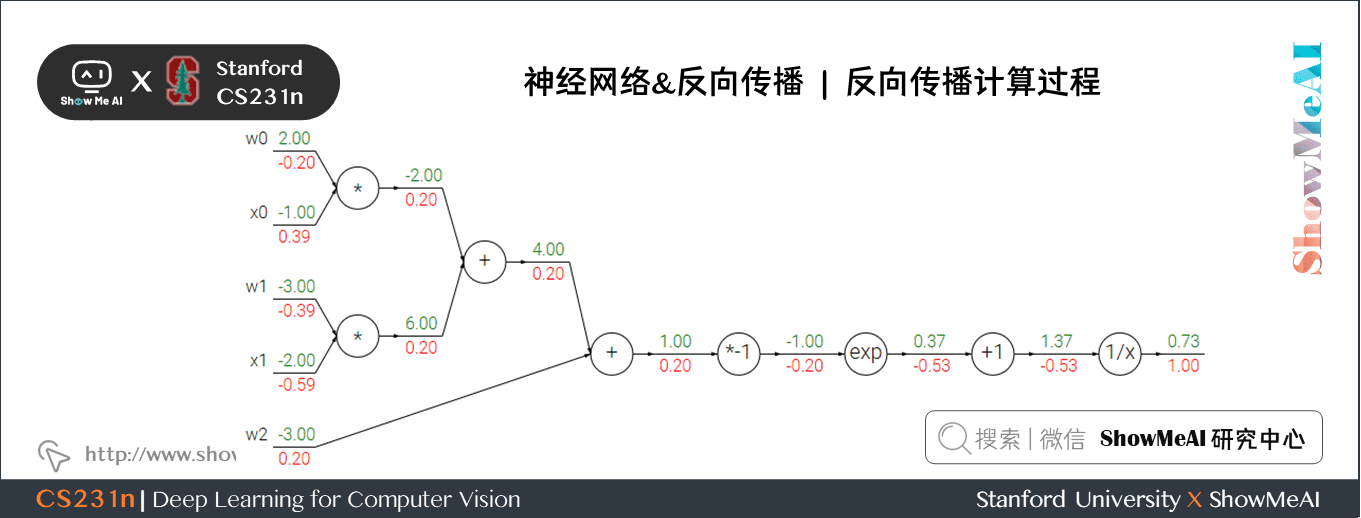
對於 $1/x$ 門單元，回傳梯度是 $1$，區域性梯度是 $-1/x^2=-1/1.37^2=-0.53$ ，所以輸入梯度為 $1 \times -0.53 = -0.53$；$+1$ 門單元不改變梯度還是 $-0.53$
exp門單元區域性梯度是 $e^x=e^{-1}$ ，然後乘回傳梯度 $-0.53$ 結果約為 $-0.2$
乘 $-1$ 門單元會將梯度加負號變為 $0.2$
加法門單元會分配梯度，所以從上到下三個加法分支都是 $0.2$
最後兩個乘法單元會轉換梯度，把回傳梯度乘另一個輸入值作為自己的梯度，得到 $-0.2$、$0.4$、$-0.4$、$-0.6$

5) Sigmoid門單元

我們可以將任何可微分的函數視作「門」。可以將多個門組合成一個門，也可以根據需要將一個函數拆成多個門。我們觀察可以發現，最右側四個門單元可以合成一個門單元，$\sigma(x) = \frac{1}{1+e^{-x}}$ ，這個函數稱為 sigmoid 函數。

sigmoid 函數可以微分：

\[\frac{d\sigma(x)}{dx} = \frac{e^{-x}}{(1+e^{-x})^2} = \left( \frac{1 + e^{-x} - 1}{1 + e^{-x}} \right) \left( \frac{1}{1+e^{-x}} \right) = \left( 1 - \sigma(x) \right) \sigma(x) \]

所以上面的例子中已經計算出 $\sigma(x)=0.73$ ，可以直接計算出乘 $-1$ 門單元輸入值的梯度為：$1 \ast (1-0.73) \ast0.73~=0.2$，計算簡化很多。

上面這個例子的反向傳播的參考 python 實現程式碼如下：

# 假設一些亂資料和權重
w = [2,-3,-3] 
x = [-1, -2]

# 前向傳播，計算輸出值
dot = w[0]*x[0] + w[1]*x[1] + w[2]
f = 1.0 / (1 + math.exp(-dot)) # sigmoid函數

# 反向傳播，計算梯度
ddot = (1 - f) * f # 點積變數的梯度, 使用sigmoid函數求導
dx = [w[0] * ddot, w[1] * ddot] # 回傳到x
dw = [x[0] * ddot, x[1] * ddot, 1.0 * ddot] # 回傳到w
# 最終得到輸入的梯度

在實際操作中，有時候我們會把前向傳播分成不同的階段，這樣可以讓反向傳播過程更加簡潔。比如建立一箇中間變數 $dot$，存放 $w$ 和 $x$ 的點乘結果。在反向傳播時，可以很快計算出裝著 $w$ 和 $x$ 等的梯度的對應的變數（比如 $ddot$，$dx$ 和 $dw$）。

本篇內容列了很多例子，我們希望通過這些例子講解「前向傳播」與「反向傳播」過程，哪些函數可以被組合成門，如何簡化，這樣他們可以「鏈」在一起，讓程式碼量更少，效率更高。

6) 分段計算範例

\[f(x,y) = \frac{x + \sigma(y)}{\sigma(x) + (x+y)^2} \]

這個表示式只是為了實踐反向傳播，如果直接對 $x,y$ 求導，運算量將會很大。下面先程式碼實現前向傳播：

x = 3  # 例子數值
y = -4

# 前向傳播
sigy = 1.0 / (1 + math.exp(-y)) # 分子中的sigmoid         #(1)
num = x + sigy # 分子                                    #(2)
sigx = 1.0 / (1 + math.exp(-x)) # 分母中的sigmoid         #(3)
xpy = x + y                                              #(4)
xpysqr = xpy**2                                          #(5)
den = sigx + xpysqr # 分母                                #(6)
invden = 1.0 / den                                       #(7)
f = num * invden

程式碼建立了多箇中間變數，每個都是比較簡單的表示式，它們計算區域性梯度的方法是已知的。可以給我們計算反向傳播帶來很多便利：

我們對前向傳播時產生的每個變數 $ (sigy, num, sigx, xpy, xpysqr, den, invden)$ 進行回傳。
我們用同樣數量的變數（以 d 開頭），儲存對應變數的梯度。
注意：反向傳播的每一小塊中都將包含了表示式的區域性梯度，然後根據使用鏈式法則乘以上游梯度。對於每行程式碼，我們將指明其對應的是前向傳播的哪部分，序號對應。

# 回傳 f = num * invden
dnum = invden # 分子的梯度                                         #(8)
dinvden = num # 分母的梯度                                         #(8)
# 回傳 invden = 1.0 / den 
dden = (-1.0 / (den**2)) * dinvden                                #(7)
# 回傳 den = sigx + xpysqr
dsigx = (1) * dden                                                #(6)
dxpysqr = (1) * dden                                              #(6)
# 回傳 xpysqr = xpy**2
dxpy = (2 * xpy) * dxpysqr                                        #(5)
# 回傳 xpy = x + y
dx = (1) * dxpy                                                   #(4)
dy = (1) * dxpy                                                   #(4)
# 回傳 sigx = 1.0 / (1 + math.exp(-x))
dx += ((1 - sigx) * sigx) * dsigx # 注意這裡用的是+=，下面有解釋    #(3)
# 回傳 num = x + sigy
dx += (1) * dnum                                                  #(2)
dsigy = (1) * dnum                                                #(2)
# 回傳 sigy = 1.0 / (1 + math.exp(-y))
dy += ((1 - sigy) * sigy) * dsigy

補充解釋：

①對前向傳播變數進行快取

在計算反向傳播時，前向傳播過程中得到的一些中間變數非常有用。
實現過程中，在程式碼裡對這些中間變數進行快取，這樣在反向傳播的時候也能用上它們。

②在不同分支的梯度要相加

如果變數 $x,y$ 在前向傳播的表示式中出現多次，那麼進行反向傳播的時候就要非常小心，要使用$+=$ 而不是 $=$ 來累計這些變數的梯度。
根據微積分中的多元鏈式法則，如果變數線上路中走向不同的分支，那麼梯度在回傳的時候，應該累加。即：

\[\frac{\partial f}{\partial x} =\sum_{q_i}\frac{\partial f}{\partial q_i}\frac{\partial q_i}{\partial x} \]

7) 實際應用

如果有一個計算圖，已經拆分成門單元的形式，那麼主類程式碼結構如下：

class ComputationalGraph(object):
    # ...
    def forward(self, inputs):
        # 把inputs傳遞給輸入門單元
        # 前向傳播計算圖
        # 遍歷所有從後向前按順序排列的門單元
        for gate in self.graph.nodes_topologically_sorted(): 
            gate.forward()  # 每個門單元都有一個前向傳播函數
        return loss  # 最終輸出損失

    def backward(self):
        # 反向遍歷門單元
        for gate in reversed(self.graph.nodes_topologically_sorted()): 
            gate.backward()  # 反向傳播函數應用鏈式法則
        return inputs_gradients  # 輸出梯度
        return inputs_gradients  # 輸出梯度

門單元類可以這麼定義，比如一個乘法單元：

class MultiplyGate(object):
    def forward(self, x, y):
        z = x*y
        self.x = x
        self.y = y
        return z

    def backward(self, dz):
        dx = self.y * dz
        dy = self.x * dz
        return [dx, dy]

1.2 向量形式反向傳播

先考慮一個簡單的例子，比如：

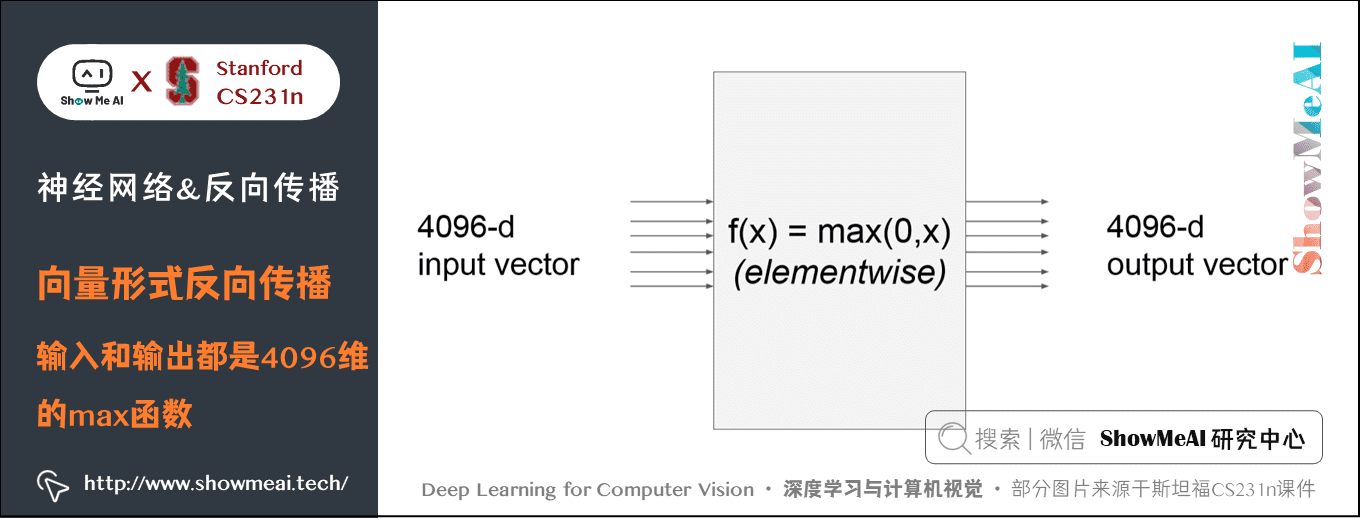
這個 $max$ 函數對輸入向量 $x$ 的每個元素都和 $0$ 比較輸出最大值，因此輸出向量的維度也是 $4096$維。此時的梯度是雅可比矩陣，即輸出的每個元素對輸入的每個元素求偏導組成的矩陣。

假如輸入 $x$ 是 $n$ 維的向量，輸出 $y$ 是 $m$ 維的向量，則 $y_1,y_2, \cdots,y_m$ 都是 $(x_1-x_n)$ 的函數，得到的雅克比矩陣如下所示：

\[\left[\begin{array}{ccc} \frac{\partial y_{1}}{\partial x_{1}} & \cdots & \frac{\partial y_{1}}{\partial x_{n}} \\ \vdots & \ddots & \vdots \\ \frac{\partial y_{m}}{\partial x_{1}} & \cdots & \frac{\partial y_{m}}{\partial x_{n}} \end{array}\right] \]

那麼這個例子的雅克比矩陣是 $[4096 \times 4096]$ 維的，輸出有 $4096$ 個元素，每一個都要求 $4096$ 次偏導。其實仔細觀察發現，這個例子輸出的每個元素都只和輸入相應位置的元素有關，因此得到的是一個對角矩陣。

實際應用的時候，往往 100 個 $x$ 同時輸入，此時雅克比矩陣是一個 $[409600 \times 409600]$ 的對角矩陣，當然只是針對這裡的 $f$ 函數。

實際上，完全寫出並儲存雅可比矩陣不太可能，因為維度極其大。

1) 一個例子

目標公式為： $f(x,W)=\vert \vert W\cdot x \vert \vert ^2=\sum_{i=1}^n (W\cdot x)_{i}^2$

其中 $x$ 是 $n$ 維的向量，$W$ 是 $n \times n$ 的矩陣。

設 $q=W\cdot x$ ,於是得到下面的式子：

\[\begin{array}{l} q=W \cdot x=\left(\begin{array}{c} W_{1,1} x_{1}+\cdots+W_{1, n} x_{n} \\ \vdots \\ W_{n, 1} x_{1}+\cdots+W_{n, n} x_{n} \end{array}\right) \\ \end{array} \]

\[f(q)=\|q\|^{2}=q_{1}^{2}+\cdots+q_{n}^{2} \]

可以看出：

$\frac{\partial f}{\partial q_i}=2q_i$ 從而得到 $f$ 對 $q$ 的梯度為 $2q$ ；
$\frac{\partial q_k}{\partial W_{i, j}}=1{i=k}x_j$，$\frac{\partial f}{\partial W_{i, j}}=\sum_{k=1}^n\frac{\partial f}{\partial q_k}\frac{\partial q_k}{\partial W_{i, j}}=\sum_{k=1}^n(2q_k)1{i=k}x_j=2q_ix_j$，從而得到 $f$ 對 $W$ 的梯度為 $2q\cdot x^T$ ；
$\frac{\partial q_k}{\partial x_i}=W_{k,i}$ ， $\frac{\partial f}{\partial x_i}=\sum_{k=1}^n\frac{\partial f}{\partial q_k}\frac{\partial q_k}{\partial x_i}=\sum_{k=1}^n(2q_k)W_{k,i}$ ，從而得到 $f$ 對 $x$ 的梯度為 $2W^T\cdot q$

下面為計算圖：

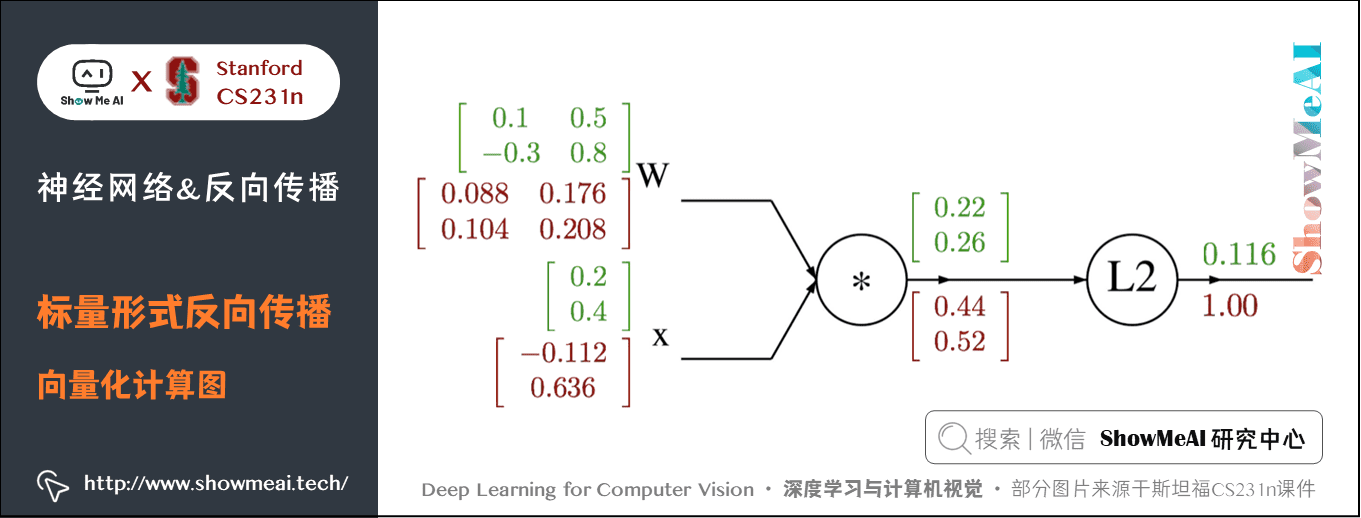
2) 程式碼實現

import numpy as np

# 初值
W = np.array([[0.1, 0.5], [-0.3, 0.8]])
x = np.array([0.2, 0.4]).reshape((2, 1))  # 為了保證dq.dot(x.T)是一個矩陣而不是實數

# 前向傳播
q = W.dot(x)
f = np.sum(np.square(q), axis=0)

# 反向傳播
# 回傳 f = np.sum(np.square(q), axis=0)
dq = 2*q
# 回傳 q = W.dot(x)
dW = dq.dot(x.T)  # x.T就是對矩陣x進行轉置
dx = W.T.dot(dq)

注意：要分析維度！不要去記憶 $dW$ 和 $dx$ 的表示式，因為它們很容易通過維度推匯出來。

權重的梯度 $dW$ 的尺寸肯定和權重矩陣 $W$ 的尺寸是一樣的

這裡的 $f$ 輸出是一個實數，所以 $dW$和 $W$ 的形狀一致。
如果考慮 $dq/dW$ 的話，如果按照雅克比矩陣的定義，$dq/dw$ 應該是 $2 \times 2 \times 2$ 維，為了減小計算量，就令其等於 $x$。
其實完全不用考慮那麼複雜，因為最終的損失函數一定是一個實數，所以每個門單元的輸入梯度一定和原輸入形狀相同。 關於這點的說明，可以點選這裡，官網進行了詳細的推導。
而這又是由 $x$ 和 $dq$ 的矩陣乘法決定的，總有一個方式是能夠讓維度之間能夠對的上的。

例如，$x$ 的尺寸是 $[2 \times 1]$，$dq$ 的尺寸是 $[2 \times 1]$，如果你想要 $dW$ 和 $W$ 的尺寸是 $[2 \times 2]$，那就要 dq.dot(x.T)，如果是 x.T.dot(dq) 結果就不對了。（$dq$ 是回傳梯度不能轉置！）

2.神經網路簡介

2.1 神經網路演演算法介紹

在不訴諸大腦的類比的情況下，依然是可以對神經網路演演算法進行介紹的。

線上性分類一節中，在給出影象的情況下，是使用 $Wx$ 來計算不同視覺類別的評分，其中 $W$ 是一個矩陣，$x$ 是一個輸入列向量，它包含了影象的全部畫素資料。在使用資料庫 CIFAR-10 的案例中，$x$ 是一個 $[3072 \times 1]$ 的列向量，$W$ 是一個 $[10 \times 3072]$ 的矩陣，所以輸出的評分是一個包含10個分類評分的向量。

一個兩層的神經網路演演算法則不同，它的計算公式是 $s = W_2 \max(0, W_1 x)$ 。

$W_1$ 的含義：舉例來說，它可以是一個 $[100 \times 3072]$ 的矩陣，其作用是將影象轉化為一個100維的過渡向量，比如馬的圖片有頭朝左和朝右，會分別得到一個分數。

函數 $max(0,-)$ 是非線性的，它會作用到每個元素。這個非線性函數有多種選擇，大家在後續啟用函數裡會再看到。現在看到的這個函數是最常用的ReLU啟用函數，它將所有小於 $0$ 的值變成 $0$。

矩陣 $W_2$ 的尺寸是 $[10 \times 100]$，會對中間層的得分進行加權求和，因此將得到 10 個數位，這10個數位可以解釋為是分類的評分。

注意：非線性函數在計算上是至關重要的，如果略去這一步，那麼兩個矩陣將會合二為一，對於分類的評分計算將重新變成關於輸入的線性函數。這個非線性函數就是改變的關鍵點。

引數 $W_1$ **,$ **W_2$ 將通過隨機梯度下降來學習到，他們的梯度在反向傳播過程中，通過鏈式法則來求導計算得出。

一個三層的神經網路可以類比地看做 $s = W_3 \max(0, W_2 \max(0, W_1 x))$ ，其中$W_1$, $W_2$ ,$W_3$ 是需要進行學習的引數。中間隱層的尺寸是網路的超引數，後續將學習如何設定它們。現在讓我們先從神經元或者網路的角度理解上述計算。

兩層神經網路參考程式碼實現如下，中間層使用 sigmoid 函數：

import numpy as np
from numpy.random import randn

N, D_in, H, D_out = 64, 1000, 100, 10
# x 是64x1000的矩陣，y是64x10的矩陣
x, y = randn(N, D_in), randn(N, D_out)
# w1是1000x100的矩陣，w2是100x10的矩陣
w1, w2 = randn(D_in, H), randn(H, D_out)

# 迭代10000次，損失達到0.0001級
for t in range(10000):
    h = 1 / (1 + np.exp(-x.dot(w1)))  # 啟用函數使用sigmoid函數，中間層
    y_pred = h.dot(w2)
    loss = np.square(y_pred - y).sum()  # 損失使用 L2 範數
    print(str(t)+': '+str(loss))

    # 反向傳播
    grad_y_pred = 2.0 * (y_pred - y)
    grad_w2 = h.T.dot(grad_y_pred)
    grad_h = grad_y_pred.dot(w2.T)
    # grad_xw1 = grad_h*h*(1-h)
    grad_w1 = x.T.dot(grad_h*h*(1-h))

    # 學習率是0.0001
    w1 -= 1e-4 * grad_w1
    w2 -= 1e-4 * grad_w2

2.2 神經網路與真實的神經對比

神經網路演演算法很多時候是受生物神經系統啟發而簡化模擬得到的。

大腦的基本計算單位是神經元（neuron） 。人類的神經系統中大約有 860 億個神經元，它們被大約 1014 - 1015 個突觸（synapses） 連線起來。下圖的上方是一個生物學的神經元，下方是一個簡化的常用數學模型。每個神經元都從它的樹突（dendrites） 獲得輸入訊號，然後沿著它唯一的軸突（axon） 產生輸出訊號。軸突在末端會逐漸分枝，通過突觸和其他神經元的樹突相連。

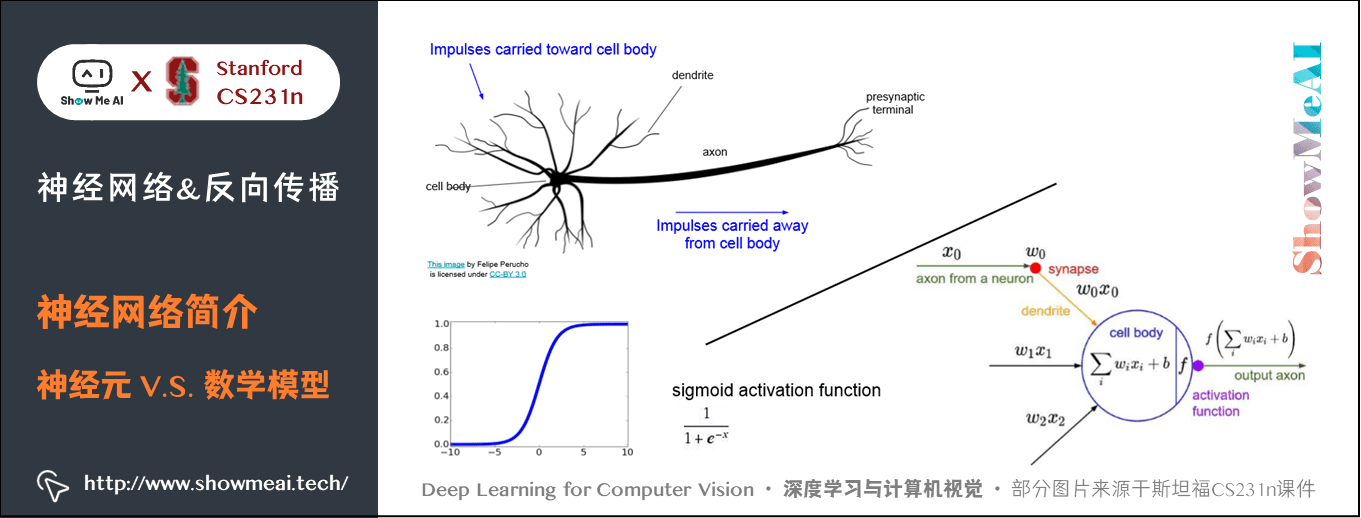
在神經元的計算模型中，沿著軸突傳播的訊號（比如 $x_0$ ）將基於突觸的突觸強度（比如 $w_0$ ），與其他神經元的樹突進行乘法互動（比如 $w_0 x_0$ ）。

對應的想法是，突觸的強度（也就是權重 $w$ ），是可學習的且可以控制一個神經元對於另一個神經元的影響強度（還可以控制影響方向：使其興奮（正權重）或使其抑制（負權重））。

樹突將訊號傳遞到細胞體，訊號在細胞體中相加。如果最終之和高於某個閾值，那麼神經元將會「啟用」，向其軸突輸出一個峰值訊號。

在計算模型中，我們假設峰值訊號的準確時間點不重要，是啟用訊號的頻率在交流資訊。基於這個速率編碼的觀點，將神經元的啟用率建模為啟用函數（activation function） $f$ ，它表達了軸突上啟用訊號的頻率。

由於歷史原因，啟用函數常常選擇使用sigmoid函數 $\sigma$ ，該函數輸入實數值（求和後的訊號強度），然後將輸入值壓縮到 $0\sim 1$ 之間。在本節後面部分會看到這些啟用函數的各種細節。

這裡的啟用函數 $f$ 採用的是 sigmoid 函數，程式碼如下：

class Neuron:
    # ...
    def neuron_tick(self, inputs):
        # 假設輸入和權重都是1xD的向量，偏差是一個數位
        cell_body_sum = np.sum(inputs*self.weights) + self.bias
        # 當和遠大於0時，輸出為1，被啟用
        firing_rate = 1.0 / (1.0 + np.exp(-cell_body_sum))
        return firing_rate

2.3 常用的啟用函數

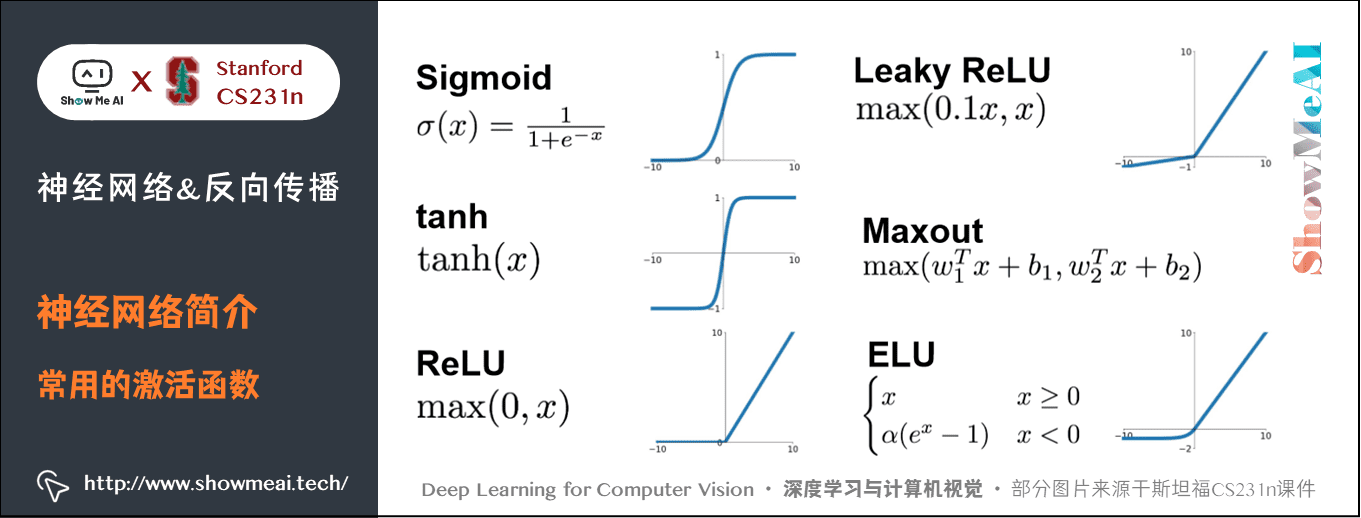
3.神經網路結構

關於神經網路結構的知識也可以參考ShowMeAI的 深度學習教學 | 吳恩達專項課程 · 全套筆記解讀 中的文章 神經網路基礎、淺層神經網路、深層神經網路 裡對於不同深度的網路結構的講解

對於普通神經網路，最普通的層級結構是全連線層（fully-connected layer）。全連線層中的神經元與其前後兩層的神經元是完全成對連線的，但是在同層內部的神經元之間沒有連線。網路結構中沒有迴圈（因為這樣會導致前向傳播的無限迴圈）。

下面是兩個神經網路的圖例，都使用的全連線層：

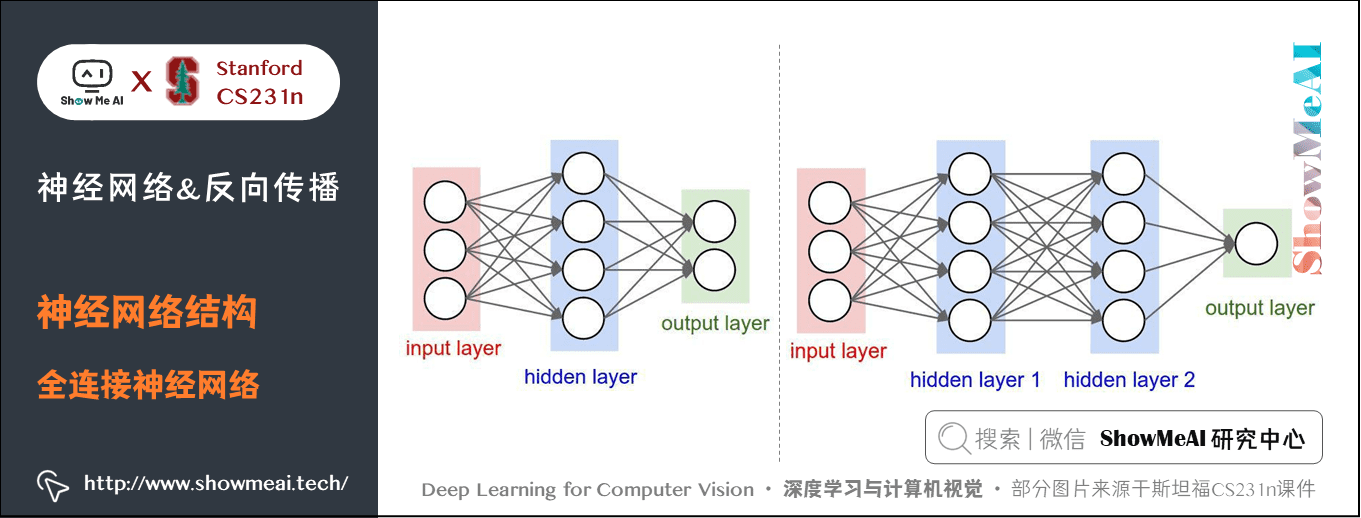
左邊：一個2層神經網路，隱層由4個神經元（也可稱為單元（unit））組成，輸出層由2個神經元組成，輸入層是3個神經元（指的是輸入圖片的維度而不是圖片的數量）。
右邊：一個3層神經網路，兩個含4個神經元的隱層。

注意：當我們說 $N$ 層神經網路的時候，我們並不計入輸入層。單層的神經網路就是沒有隱層的（輸入直接對映到輸出）。也會使用人工神經網路（Artificial Neural Networks 縮寫ANN）或者多層感知器（Multi-Layer Perceptrons 縮寫MLP）來指代全連線層構建的這種神經網路。此外，輸出層的神經元一般不含啟用函數。

用來度量神經網路的尺寸的標準主要有兩個：一個是神經元的個數，另一個是引數的個數。用上面圖示的兩個網路舉例：

第一個網路有 $4+2=6$ 個神經元（輸入層不算），$[3 \times 4]+[4 \times 2]=20$ 個權重，還有$4+2=6$ 個偏置，共 $26$ 個可學習的引數。
第二個網路有 $4+4+1=9$ 個神經元，$[3 \times 4]+[4 \times 4]+[4 \times 1]=32$ 個權重，$4+4+1=9$ 個偏置，共 $41$ 個可學習的引數。

現代折積神經網路能包含上億個引數，可由幾十上百層構成（這就是深度學習）。

3.1 三層神經網路程式碼範例

不斷用相似的結構堆疊形成網路，這讓神經網路演演算法使用矩陣向量操作變得簡單和高效。我們回到上面那個3層神經網路，輸入是 $[3 \times 1]$ 的向量。一個層所有連線的權重可以存在一個單獨的矩陣中。

比如第一個隱層的權重 $W_1$ 是 $[4 \times 3]$，所有單元的偏置儲存在 $b_1$ 中，尺寸 $[4 \times 1]$。這樣，每個神經元的權重都在 $W_1$ 的一個行中，於是矩陣乘法 np.dot(W1, x)+b1 就能作為該層中所有神經元啟用函數的輸入資料。類似的，$W_2$ 將會是 $[4 \times 4]$ 矩陣，儲存著第二個隱層的連線，$W_3$ 是 $[1 \times 4]$ 的矩陣，用於輸出層。

完整的3層神經網路的前向傳播就是簡單的3次矩陣乘法，其中交織著啟用函數的應用。

import numpy as np

# 三層神經網路的前向傳播
# 啟用函數
f = lambda x: 1.0/(1.0 + np.exp(-x))

# 隨機輸入向量3x1
x = np.random.randn(3, 1)
# 設定權重和偏差
W1, W2, W3 = np.random.randn(4, 3), np.random.randn(4, 4), np.random.randn(1, 4),
b1, b2= np.random.randn(4, 1), np.random.randn(4, 1)
b3 = 1

# 計算第一個隱藏層啟用 4x1
h1 = f(np.dot(W1, x) + b1)
# 計算第二個隱藏層啟用 4x1
h2 = f(np.dot(W2, h1) + b2)
# 輸出是一個數
out = np.dot(W3, h2) + b3

在上面的程式碼中，$W_1$，$W_2$，$W_3$，$b_1$，$b_2$，$b_3$ 都是網路中可以學習的引數。注意 $x$ 並不是一個單獨的列向量，而可以是一個批次的訓練資料（其中每個輸入樣本將會是 $x$ 中的一列），所有的樣本將會被並行化的高效計算出來。

注意神經網路最後一層通常是沒有啟用函數的（例如，在分類任務中它給出一個實數值的分類評分）。

全連線層的前向傳播一般就是先進行一個矩陣乘法，然後加上偏置並運用啟用函數。

3.2 理解神經網路

關於深度神經網路的解釋也可以參考ShowMeAI的 深度學習教學 | 吳恩達專項課程 · 全套筆記解讀 中的文章 深層神經網路 裡「深度網路其他優勢」部分的講解

全連線層的神經網路的一種理解是：

它們定義了一個由一系列函陣列成的函數族，網路的權重就是每個函數的引數。

擁有至少一個隱層的神經網路是一個通用的近似器，神經網路可以近似任何連續函數。

雖然一個2層網路在數學理論上能完美地近似所有連續函數，但在實際操作中效果相對較差。雖然在理論上深層網路（使用了多個隱層）和單層網路的表達能力是一樣的，但是就實踐經驗而言，深度網路效果比單層網路好。

對於全連線神經網路而言，在實踐中3層的神經網路會比2層的表現好，然而繼續加深（做到4，5，6層）很少有太大幫助。折積神經網路的情況卻不同，在折積神經網路中，對於一個良好的識別系統來說，深度是一個非常重要的因素（比如當今效果好的CNN都有幾十上百層）。對於該現象的一種解釋觀點是：因為影象擁有層次化結構（比如臉是由眼睛等組成，眼睛又是由邊緣組成），所以多層處理對於這種資料就有直觀意義。

4.拓展學習

可以點選 B站檢視視訊的【雙語字幕】版本

5.要點總結

前向傳播與反向傳播
標量與向量化形式計算
求導鏈式法則應用
神經網路結構
啟用函數
理解神經網路