程式分析與優化
本章是系列文章的第五章,介紹了指標分析方法。指標分析在C/C++語言中非常重要,分析的結果可以有效提升指標的優化效率。
本文中的所有內容來自學習DCC888的學習筆記或者自己理解的整理,如需轉載請註明出處。周榮華@燧原科技
5.1 概念
- 指標是許多重要程式語言的特性之一
- 指標的使用,可以避免大量的資料拷貝
- 指標的分析的難度很大,並且一直是理解和修改程式的主要障礙
- 指標分析(Pointer Analysis),又可以稱為別名分析(Alias Analysis),或者指向分析(Points-To Analysis)
5.2 為什麼需要指標分析
1 #include <stdio.h> 2 int main() { 3 int i = 7; 4 int *p = &i; 5 *p = 13; 6 printf("The value of i = %d\n", i); 7 }
給定上面的例子。gcc的-O1選項能優化成什麼樣子?
將上述程式碼儲存到pta5.1.cc,並使用「gcc -O1 pta5.1.cc -S」進行編譯,生成的組合程式碼如下:
1 .file "pta5.1.cc" 2 .section .rodata.str1.1,"aMS",@progbits,1 3 .LC0: 4 .string "The value of i = %d\n" 5 .text 6 .globl main 7 .type main, @function 8 main: 9 .LFB30: 10 .cfi_startproc 11 subq $8, %rsp 12 .cfi_def_cfa_offset 16 13 movl $13, %edx 14 movl $.LC0, %esi 15 movl $1, %edi 16 movl $0, %eax 17 call __printf_chk 18 movl $0, %eax 19 addq $8, %rsp 20 .cfi_def_cfa_offset 8 21 ret 22 .cfi_endproc 23 .LFE30: 24 .size main, .-main 25 .ident "GCC: (Ubuntu 5.4.0-6ubuntu1~16.04.12) 5.4.0 20160609" 26 .section .note.GNU-stack,"",@progbits
從組合程式碼看,程式直接忽略掉了第3行和第4行的初始化和傳地址操作,直接實現了第5行的賦值和第6行的列印。效能是不是強大了很多。
再看個例子:
1 #include <stdio.h> 2 #include <stdlib.h> 3 void sum0(int *a, int *b, int *r, int N) { 4 int i; 5 for (i = 0; i < N; i++) { 6 r[i] = a[i]; 7 if (!b[i]) { 8 r[i] = b[i]; 9 } 10 } 11 } 12 void sum1(int *a, int *b, int *r, int N) { 13 int i; 14 for (i = 0; i < N; i++) { 15 int tmp = a[i]; 16 if (!b[i]) { 17 tmp = b[i]; 18 } 19 r[i] = tmp; 20 } 21 } 22 void print(int *a, int N) { 23 int i; 24 for (i = 0; i < N; i++) { 25 if (i % 10 == 0) { 26 printf("\n"); 27 } 28 printf("%8d", a[i]); 29 } 30 } 31 #define SIZE 10000 32 #define LOOP 100000 33 int main(int argc, char **argv) { 34 int *a = (int *)malloc(SIZE * 4); 35 int *b = (int *)malloc(SIZE * 4); 36 int *c = (int *)malloc(SIZE * 4); 37 int i; 38 for (i = 0; i < SIZE; i++) { 39 a[i] = i; 40 b[i] = i % 2; 41 } 42 if (argc % 2) { 43 printf("sum0\n"); 44 for (i = 0; i < LOOP; i++) { 45 sum0(a, b, c, SIZE); 46 } 47 } else { 48 printf("sum1\n"); 49 for (i = 0; i < LOOP; i++) { 50 sum1(a, b, c, SIZE); 51 } 52 } 53 }
在教材中提供的編譯器編譯的結果看,-O1無法有效優化sum0的指標操作,但對sum1手工優化後的程式碼能很好的進行指標優化。這是教材中提供的執行資料:
1 $> time ./a.out 2 sum0 3 0 1 0 3 4 0 11 0 13 5 real 0m6.299s 6 user 0m6.285s 7 sys 0m0.008s 8 $> time ./a.out a 9 sum1 10 0 1 0 3 11 0 11 0 13 12 real 0m1.345s 13 user 0m1.340s 14 sys 0m0.004s
但我用gcc5編譯實測下來的結果是-O0,確實不會優化,-O1仍然有很好的優化(時間是-O0的十分之一),並且sum0和sum1效能上差別不大,說明編譯器進化的非常快。
1 ronghua.zhou@794bb5fbd58a:~/DCC888$ gcc pta5.2.c -O0 2 ronghua.zhou@794bb5fbd58a:~/DCC888$ time ./a.out 3 sum0 4 5 real 0m5.772s 6 user 0m5.767s 7 sys 0m0.004s 8 ronghua.zhou@794bb5fbd58a:~/DCC888$ time ./a.out a 9 sum1 10 11 real 0m4.766s 12 user 0m4.761s 13 sys 0m0.004s 14 ronghua.zhou@794bb5fbd58a:~/DCC888$ gcc pta5.2.c -O1 15 ronghua.zhou@794bb5fbd58a:~/DCC888$ time ./a.out 16 sum0 17 18 real 0m0.542s 19 user 0m0.541s 20 sys 0m0.000s 21 ronghua.zhou@794bb5fbd58a:~/DCC888$ time ./a.out a 22 sum1 23 24 real 0m0.473s 25 user 0m0.473s 26 sys 0m0.000s
由於sum0和sum1本身計算時間相差不大,所以外面主要對比一下sum0在-O0時的程式碼和-O1時的程式碼的差別。
不優化的結果:
1 sum0: 2 .LFB2: 3 .cfi_startproc 4 pushq %rbp 5 .cfi_def_cfa_offset 16 6 .cfi_offset 6, -16 7 movq %rsp, %rbp 8 .cfi_def_cfa_register 6 9 movq %rdi, -24(%rbp) 10 movq %rsi, -32(%rbp) 11 movq %rdx, -40(%rbp) 12 movl %ecx, -44(%rbp) 13 movl $0, -4(%rbp) 14 jmp .L2 15 .L4: 16 movl -4(%rbp), %eax 17 cltq 18 leaq 0(,%rax,4), %rdx 19 movq -40(%rbp), %rax 20 addq %rax, %rdx 21 movl -4(%rbp), %eax 22 cltq 23 leaq 0(,%rax,4), %rcx 24 movq -24(%rbp), %rax 25 addq %rcx, %rax 26 movl (%rax), %eax 27 movl %eax, (%rdx) 28 movl -4(%rbp), %eax 29 cltq 30 leaq 0(,%rax,4), %rdx 31 movq -32(%rbp), %rax 32 addq %rdx, %rax 33 movl (%rax), %eax 34 testl %eax, %eax 35 jne .L3 36 movl -4(%rbp), %eax 37 cltq 38 leaq 0(,%rax,4), %rdx 39 movq -40(%rbp), %rax 40 addq %rax, %rdx 41 movl -4(%rbp), %eax 42 cltq 43 leaq 0(,%rax,4), %rcx 44 movq -32(%rbp), %rax 45 addq %rcx, %rax 46 movl (%rax), %eax 47 movl %eax, (%rdx) 48 .L3: 49 addl $1, -4(%rbp) 50 .L2: 51 movl -4(%rbp), %eax 52 cmpl -44(%rbp), %eax 53 jl .L4 54 nop 55 popq %rbp 56 .cfi_def_cfa 7, 8 57 ret 58 .cfi_endproc 59 .LFE2: 60 .size sum0, .-sum0 61 .globl sum1 62 .type sum1, @function
O1優化後的結果:
1 sum0: 2 .LFB38: 3 .cfi_startproc 4 testl %ecx, %ecx 5 jle .L1 6 movl $0, %eax 7 .L4: 8 movl (%rdi,%rax,4), %r9d 9 movl %r9d, (%rdx,%rax,4) 10 movl (%rsi,%rax,4), %r8d 11 testl %r8d, %r8d 12 cmovne %r9d, %r8d 13 movl %r8d, (%rdx,%rax,4) 14 addq $1, %rax 15 cmpl %eax, %ecx 16 jg .L4 17 .L1: 18 rep ret 19 .cfi_endproc 20 .LFE38: 21 .size sum0, .-sum0 22 .globl sum1 23 .type sum1, @function
這個函數從O0到O1的優化過程中使用了很多優化方法,對於這裡說的指標分析,由於指標的求地址和解除參照非常耗時,O1使用cmovne將必要和拷貝優化成單個指令,起到了很好的效果。
在大多數情況下,sum0和sum1是等價的,但如果b和r這2個指標指向同一個地址的時候,2個演演算法就會有一些差別,所以編譯器不能直接將sum0優化成sum1。
5.3 指標分析
指標分析的目標是找到每個指標指向的地址。
指標分析經常使用基於約束系統的分析方法來描述和解決。
效能最好的指標分析演演算法的複雜度是O(n3)。
為了提升效率和精準度,指標分析是編譯器設計中僅次於暫存器分配方法的第二大課題。
5.4 嘗試使用資料流分析方法解決指標分析
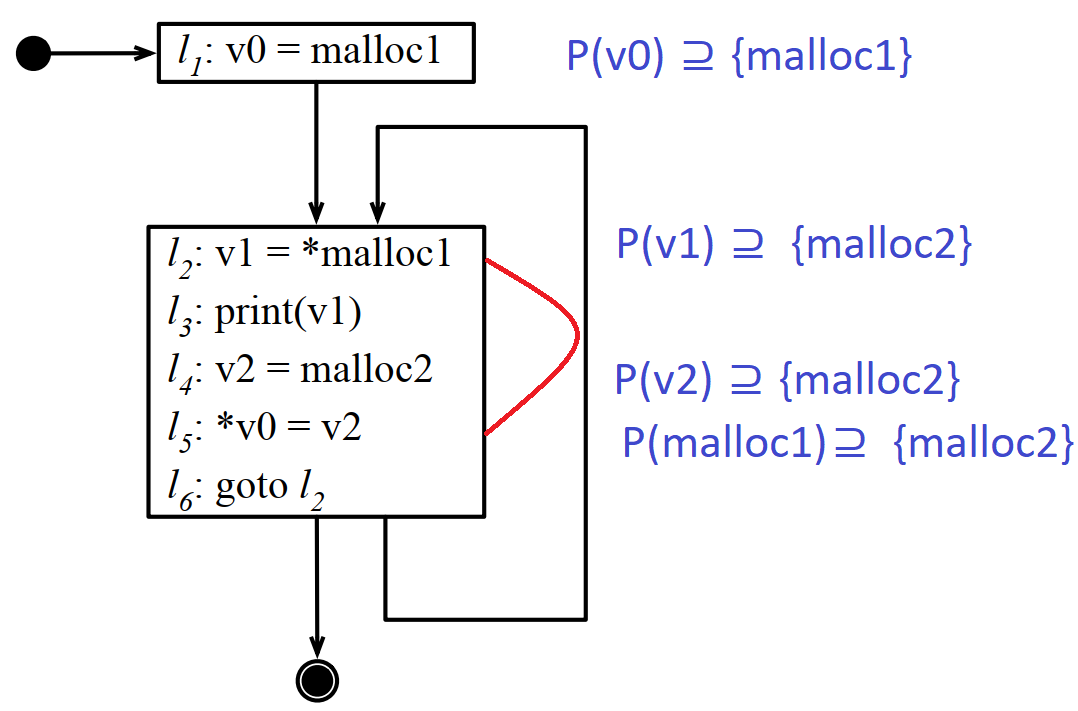
如下圖所示,由於l2和l5會相互影響,但很難通過簡單的語法分析就能找到他們之間的聯絡,所以基本的資料流分析對指標分析會失效。
5.5 ANDERSEN指標分析演演算法
常見的四種指標構造過程(控制流分析裡面原來用⊆表達右邊是左邊的約束,但這個很容易和之前求指標分析時的約束弄混,因為約束是⊇,換算成控制流要轉向成⊆,不知道別人會不會暈,反正我被弄暈了。所以最後我改成<-表示控制流圖裡面的邊的方向,這樣看著稍微好懂點):
|
指令
|
約束名
|
約束
|
控制流分析結果
|
|---|---|---|---|
| a = &b | base | P(a)⊇ {b} | lhs <- rhs |
| a = b | simple | P(a)⊇ P(b) | lhs <- rhs |
| a = *b | load | t ∈ P(b)⇒ P(a)⊇ P(t) | {t} <- rhs' ⇒ lhs <- rhs |
| *a = b | store | t ∈ P(a)⇒ P(t)⊇ P(b) | {t} <- rhs' ⇒ lhs <- rhs |
Andersen指標分析法,又稱為基於集合包含的的約束分析法。
Anderson的指向圖演演算法:
1 let G = (V, E) 2 W = V 3 while W ≠ [] do 4 n = hd(W) 5 for each v ∈ P(n) do 6 for each load "a = *n" do 7 if (v, a) ∉ E then 8 E = E ∪ {(v, a)} 9 W = v::W 10 for each store "*n = b" do 11 if (b, v) ∉ E then 12 E = E ∪ {(v, a)} 13 W = b::W 14 for each (n, z) ∈ E do 15 P(z) = P(z) ∪ P(n) 16 if P(z) has changed then 17 W = z::W
上面的演演算法做一些解釋:
W = v::W 的含義是將W這個陣列的頭部增加一個元素v。
n = hd(W) 表示從陣列W中取出頭結點,賦值給n。
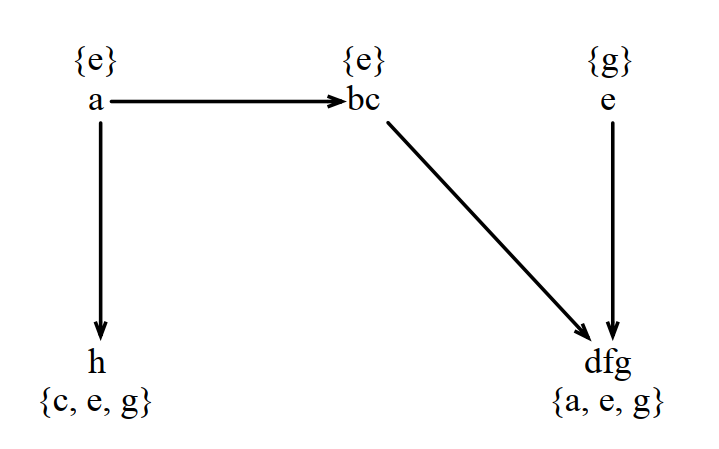
例如,對下面的程式碼:
1 b = &a 2 a = &c 3 d = a 4 *d = b 5 a = *d
生成的指向圖是這樣的:
5.6 迴圈坍塌(COLLAPSING CYCLES)
找到圖的傳遞閉包的演演算法複雜度達到O(n3),使得科學家們一直沒停止過對它的優化。
迴圈坍塌是二十一世紀出發現的一種優化方法,迴圈坍塌的理論基礎是強連通圖的拓撲一致性,在指向分析圖中,表示形成迴圈的所有節點,都有一致的指向分析集合。
演演算法能用和演演算法在實際中能用是兩個概念。
5.6.1 迴圈識別
DFS可以發現迴圈,但發現的複雜度也不低。DFS的目標是遍歷所有節點,但如果想要通過DFS發現環的話,就不但要記錄節點,還要記錄節點的所有邊,這樣才能區別一個節點的子結點已經遍歷過的情況下判斷出只是菱形依賴,還是環。
常見的迴圈識別方法有波傳遞演演算法(Wave propagation),深度傳遞演演算法(Deep propagation)和惰性迴圈檢測方法(Lazy cycle detection)。
5.6.2 惰性迴圈檢測(Lazy Cycle Detection)
參見The ant and the grasshopper: fast and accurate pointer analysis for millions of lines of code, 2007。這篇文章實際提出了兩種迴圈檢測方法,一種是惰性迴圈檢測,一種是混合迴圈檢測。
增加惰性迴圈檢測之後的演演算法相對於沒有迴圈檢測的方法,主要增加了第2行和第16~18行。其中第2行是增加了一個集合初始化(用來避免重複進行迴圈檢測)。16~18行主要是發現某條邊的2個節點的指向集合相等的情況下觸發迴圈檢測,檢測成功就直接觸發迴圈坍塌。不論是否檢測到迴圈,都會將疑似迴圈的邊加入到已檢測的集合中。
1 let G = (V, E) 2 R = {} 3 W = V 4 while W ≠ [] do 5 n = hd(W) 6 for each v ∈ P(n) do 7 for each load "a = *n" do 8 if (v, a) ∉ E then 9 E = E ∪ {(v, a)} 10 W = v::W 11 for each store "*n = b" do 12 if (b, v) ∉ E then 13 E = E ∪ {(v, a)} 14 W = b::W 15 for each (n, z) ∈ E do 16 if P(z) = P(n) and (n, z) ∉ R then 17 DETECTANDCOLLAPSECYCLES(z) 18 R = R∪ {(n, z)} 19 P(z) = P(z) ∪ P(n) 20 if P(z) has changed then 21 W = z::W
優點:僅在非常大可能效能找到環的情況下才觸發環形檢測;概念簡單,容易實現。
缺點:觸發檢測前環已經存在一段時間,會降低部分效能;即使概率很大的時候,環形檢測還是有可能失敗(當前還沒有失敗的證據)。
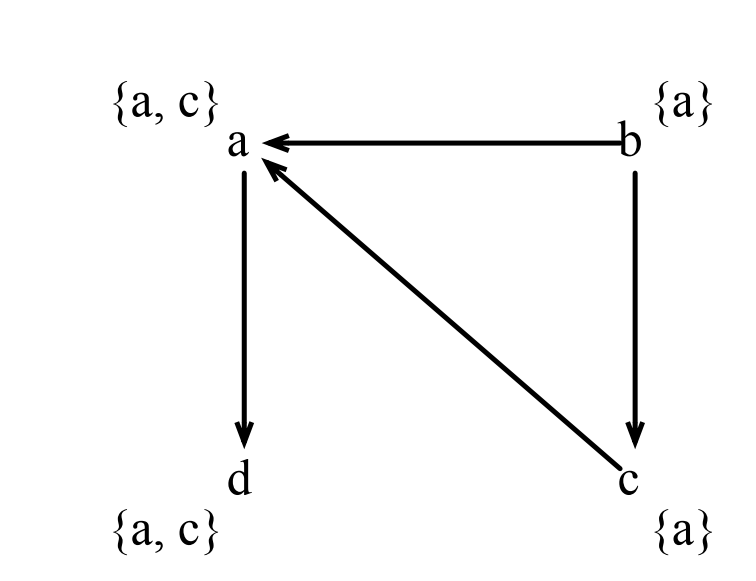
對下面的虛擬碼:
1 c = &d 2 e = &a 3 a = b 4 b = c 5 c = *e
生成的指向圖如下(其中a/b/c觸發了迴圈坍塌):

5.6.3 波傳遞演演算法(Wave Propagation)
波傳遞演演算法的虛擬碼如下:
1 repeat 2 changed = false 3 collapse Strongly Connected Components 4 WAVEPROPAGATION 5 ADDNEWEDGES 6 if a new edge has been added to G then 7 changed = true 8 until changed = false 9 10 11 WAVEPROPAGATION(G, P, T) 12 while T ≠ [] 13 v = hd(T) 14 Pdif = Pcur(v) – Pold(v) 15 Pold(v) = Pcur(v) 16 if Pdif ≠ {} 17 for each w such that (v, w) ∈ E do 18 Pcur(w) = Pcur(w) ∪ Pdif 19 20 21 ADDNEWEDGES(G = (E, V), C) 22 for each operation c such as l = *r ∈ C do 23 Pnew = Pcur(r) – Pcache(c) 24 Pcache(c) = Pcache(c) ∪ Pnew 25 for each v ∈ Pnew do 26 if (v, l) ∉ E then 27 E = E ∪ {(v, l)} 28 Pcur(l) = Pcur(l) ∪ Pold(v) 29 for each operation c such as *l = r do 30 Pnew = Pcur(l) – Pcache(c) 31 Pcache(c) = Pcache(c) ∪ Pnew 32 for each v ∈ Pnew do 33 if (r, v) ∉ E then 34 E = E ∪ {(r, v)} 35 Pcur(v) = Pcur(v) ∪ Pold(r)
上述演演算法中的引數的含義如下:
- G:指向圖
- P:指向集合
- T:G中所有節點的拓撲順序
- Pcache:上一次計算出來的指向集合,初始化為{}
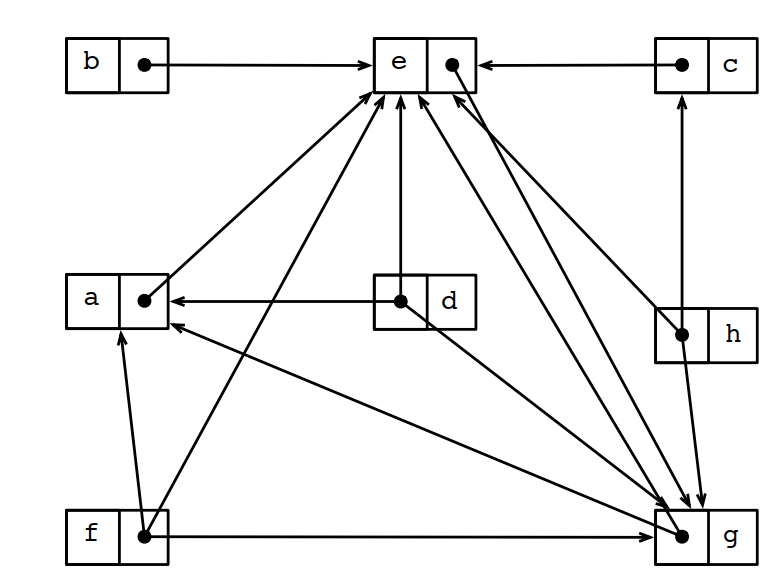
對下面的虛擬碼:
1 h = &c 2 e = &g 3 b = c 4 h = &g 5 h = a 6 c = b 7 a = &e 8 f = d 9 b = a 10 d = *h 11 *e = f 12 f = &a
生成的指向圖如下(其中b/c和d/f/g觸發了迴圈坍塌):
5.7 STEENSGAARD指標分析演演算法
如果把Anderson指標分析演演算法中的集合包含換成等號(將包含符號左右兩側的集合先求並集,然後賦值給原來的兩個集合),就形成了Steensgaard指標分析演演算法,也稱為基於集合並集的指標分析演演算法。
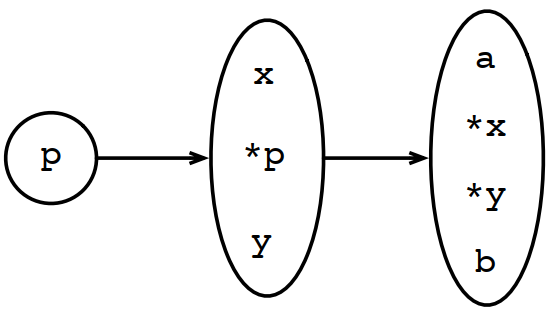
對下面的虛擬碼:
1 x = &a; 2 y = &b; 3 p = &x; 4 p = &y;
生成的指向圖如下:
5.7.1 Union-Find
基於鏈式並集計算的複雜度可以達到α(n),其中α是Ackermann function的簡稱,該演演算法實現也稱為Union-Find。演演算法的具體描述參見An Improved Equivalence Algorithms (1964)。
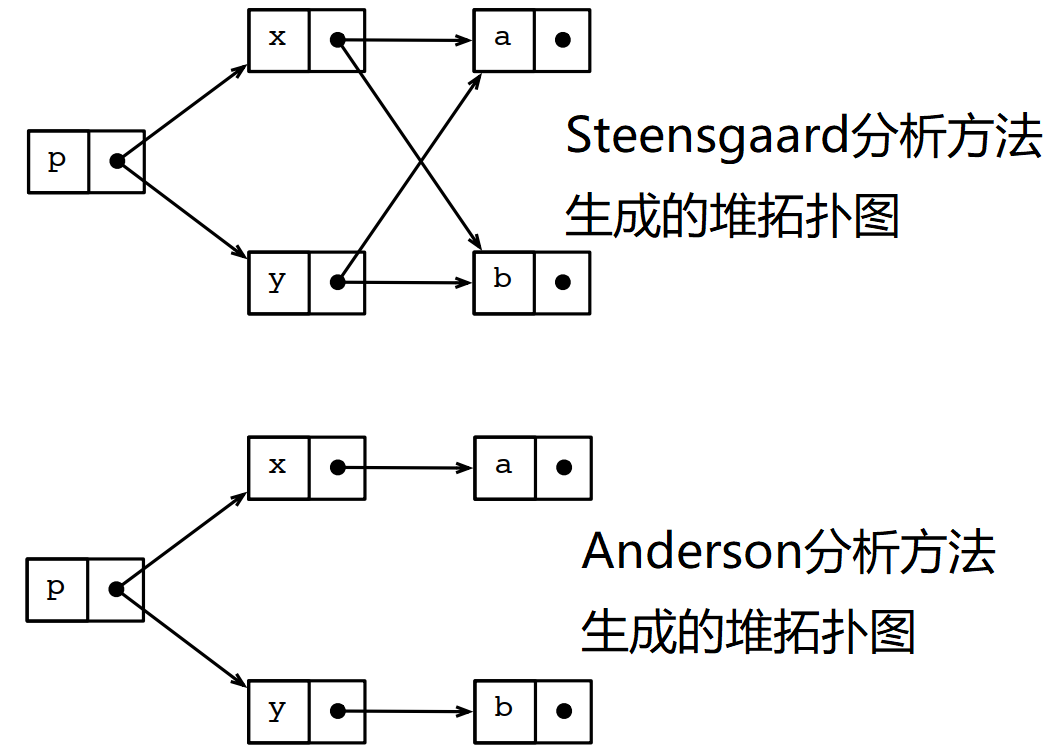
5.7.2 Steensgaard指標分析演演算法沒有Anderson指標分析演演算法精準
例如上面例子生成的兩個堆的拓撲圖,按Steensgaard的分析結論,x可能指向b,y可能指向a。但Anderson的分析結論,x不可能指向b,y不可能指向a,顯然Anderson的分析結論更接近事實。
5.8 總結
5.8.1 一種通用模式(A Common Pattern)
迄今為止,所有分析演演算法都遵循一種模式:迭代,直到找到一個不動點(也就是說,如果某次迭代後,所有變數都不變,後面再觸發迭代,也不會再改變)。
這個通用模式適用於資料流分析、控制流分析和指向分析。
5.8.2 流相關性(Flow Sensitiveness)
儘管Anderson分析演演算法比Steensgaard演演算法精確,但由於它是流無關演演算法,所以仍然存在一些結論是實際執行中不可能出現,或者不可能同時出現的,這就是流無關分析演演算法(Flow Insensitive)的侷限性。
但是如果按照流相關分析演演算法(Flow Sensitive)進行分析,每個程式點都需要保留一份獨立的分析結論,這對大規模程式的分析是非常昂貴的(常常會帶來OOM:))。
5.8.3 指標分析簡史
- Andersen, L. "Program Analysis and Specialization for the C Programming Language", PhD Thesis, University of Copenhagen, (1994)
- Hardekopf, B. and Lin, C. "The Ant and the Grasshopper: fast and accurate pointer analysis for millions of lines of code", PLDI, pp 290-299 (2007)
- Pereira, F. and Berlin, D. "Wave Propagation and Deep Propagation for Pointer Analysis", CGO, pp 126-135 (2009)
- Steensgaard, B., "Points-to Analysis in Almost Linear Time", POPL, pp 32-41 (1995)