技術文章 » 分散式機器學習：邏輯迴歸的並行化實現（PySpark）

分散式機器學習：邏輯迴歸的並行化實現（PySpark）

2022-05-27 21:00:25

1. 梯度計算式匯出

我們在部落格《統計學習：邏輯迴歸與交叉熵損失（Pytorch實現）》中提到，設\(w\)為權值(最後一維為偏置)，樣本總數為\(N\)，\(\{(x_i, y_i)\}_{i=1}^N\)為訓練樣本集。樣本維度為\(D\)，\(x_i\in \mathbb{R}^{D+1}\)（最後一維擴充），\(y_i\in\{0, 1\}\)。則邏輯迴歸的損失函數為：

\[\mathcal{l}(w) = \sum_{i=1}^{N}\left[y_{i} \log \pi_{w}\left(x_{i}\right)+\left(1-y_{i}\right) \log \left(1-\pi_w\left(x_{i}\right)\right)\right] \]

這裡

\[\begin{aligned} \pi_w(x) = p(y=1 \mid x; w) =\frac{1}{1+\exp \left(-w^{T} x\right)} \end{aligned} \]

寫成這個形式就已經可以用諸如Pytorch這類工具來進行自動求導然後採用梯度下降法求解了。不過若需要用表示式直接計算出梯度，我們還需要將損失函數繼續化簡為：

\[\mathcal{l}(w) = -\sum_{i=1}^N(y_i w^T x_i - \log(1 + \exp(w^T x_i))) \]

可將梯度表示如下：

\[\nabla_w{\mathcal{l}(w)} = -\sum_{i=1}^N(y_i - \frac{1}{\exp(-w^Tx)+1})x_i \]

2. 基於Spark的並行化實現

邏輯迴歸的目標函數常採用梯度下降法求解，該演演算法的並行化可以採用如下的Map-Reduce架構：

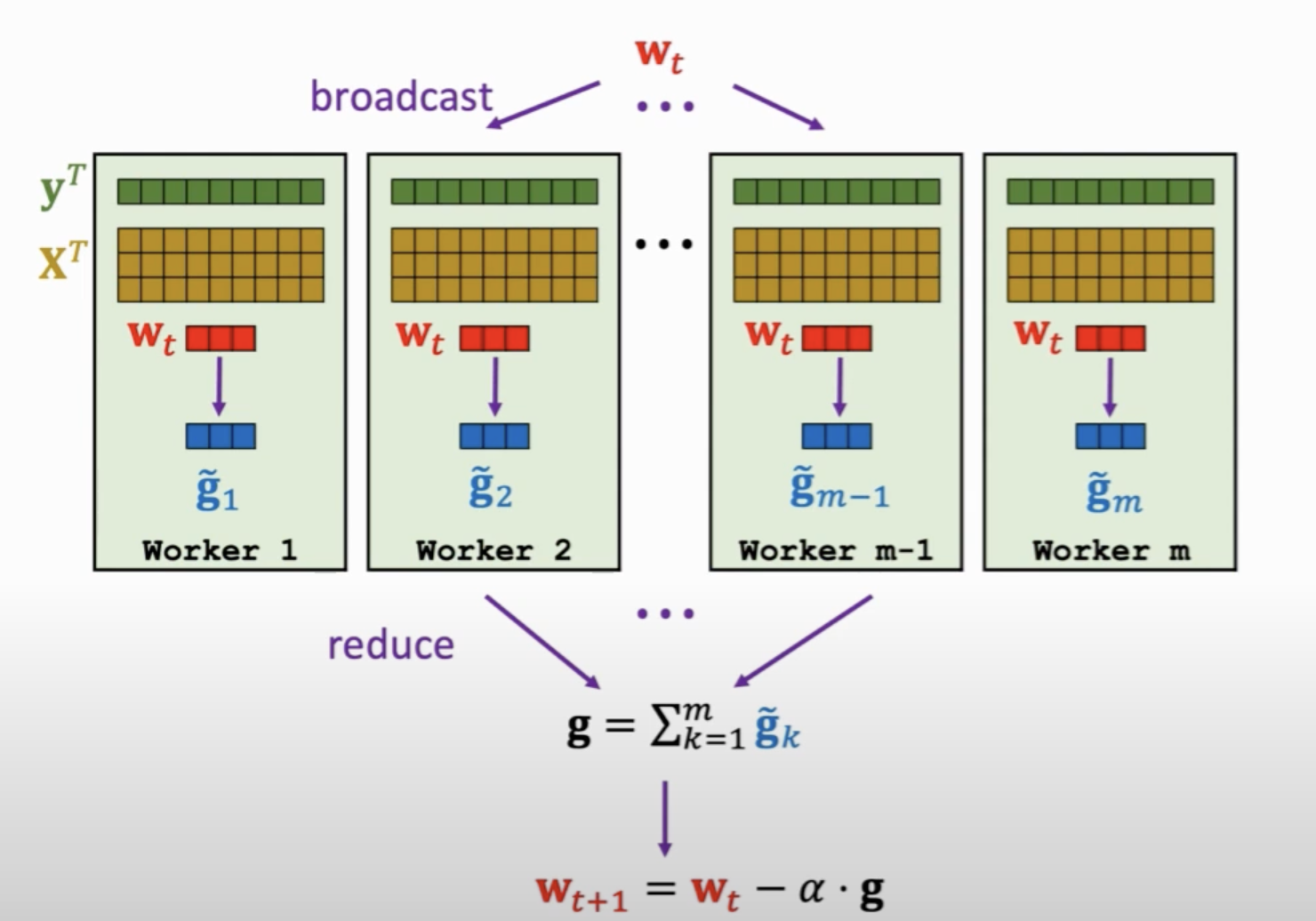
先將第\(t\)輪迭代的權重廣播到各worker，各worker計算一個區域性梯度（map過程），然後再將每個節點的梯度聚合（reduce過程），最終對引數進行更新。

在Spark中每個task對應一個分割區，決定了計算的並行度(分割區的概念詳間我們上一篇部落格《Spark: 單詞計數(Word Count)的MapReduce實現(Java/Python)》 )。在Spark的實現過程如下：

  • map階段： 各task執行map()函數對每個樣本\((x_i, y_i)\)計算梯度\(g_i\)， 然後對每個樣本對應的梯度執行進行本地聚合，以減少後面的資料傳輸量。如第1個task執行reduce()操作得到\(\widetilde{g}_1 = \sum_{i=1}^3 g_i\) 如下圖所示：

  • reduce階段：使用reduce()將所有task的計算結果收集到Driver端進行聚合，然後進行引數更新。

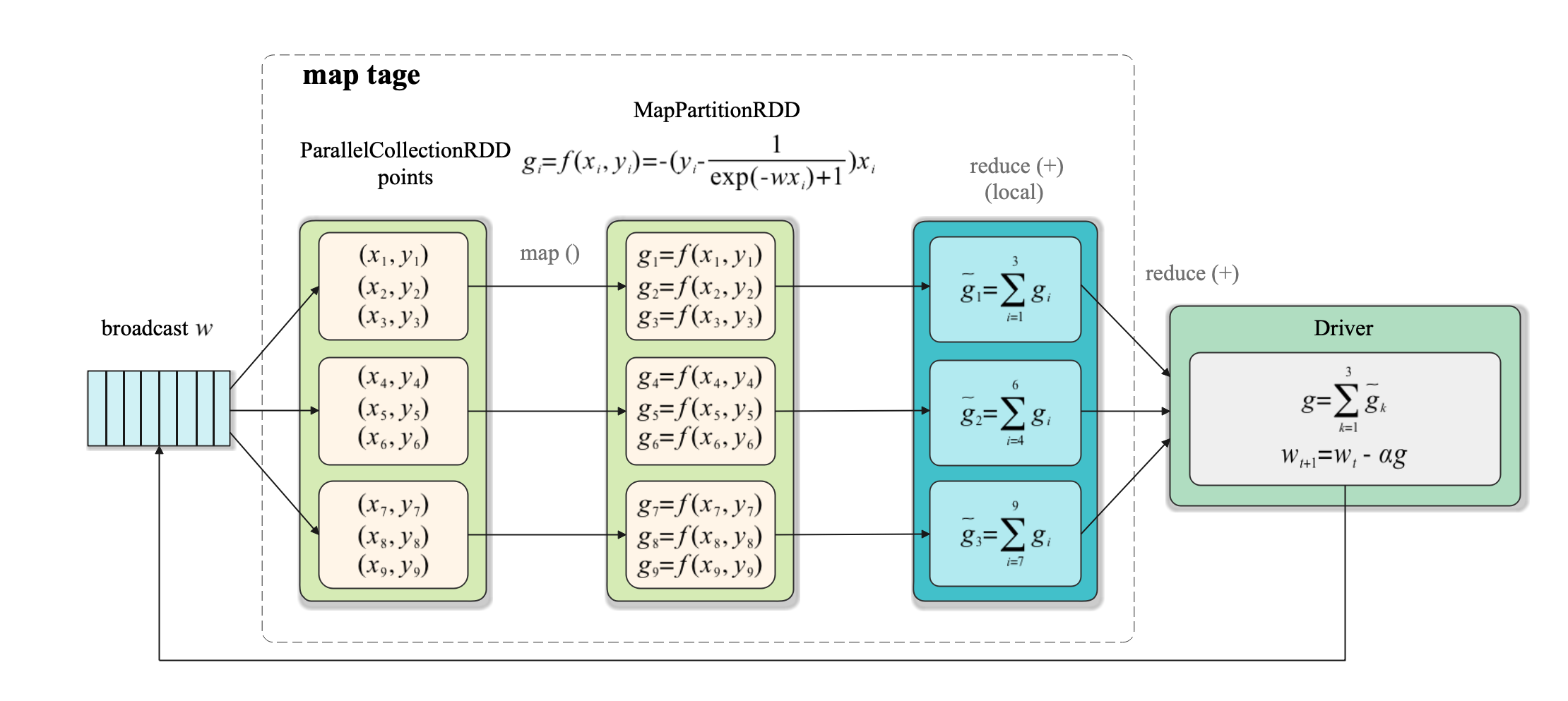
在上圖中，訓練資料用points:PrallelCollectionRDD來表示，引數向量用\(w\)來表示，注意引數向量不是RDD，只是一個單獨的參與運算的變數。

此外需要注意一點，雖然每個task在本地進行了區域性聚合，但如果task過多且每個task本地聚合後的結果（單個gradient）過大那麼統一傳遞到Driver端仍然會造成單點的網路平均等問題。為了解決這個問題，Spark設計了效能更好的treeAggregate()操作，使用樹形聚合方法來減少網路和計算延遲。

3. PySpark實現程式碼

PySpark的完整實現程式碼如下：

from sklearn.datasets import load_breast_cancer
import numpy as np
from pyspark.sql import SparkSession
from operator import add
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score

n_slices = 3  # Number of Slices
n_iterations = 300  # Number of iterations
alpha = 0.01  # iteration step_size


def logistic_f(x, w):
    return 1 / (np.exp(-x.dot(w)) + 1)


def gradient(point: np.ndarray, w: np.ndarray) -> np.ndarray:
    """ Compute linear regression gradient for a matrix of data points
    """
    y = point[-1]    # point label
    x = point[:-1]   # point coordinate
    # For each point (x, y), compute gradient function, then sum these up
    return - (y - logistic_f(x, w)) * x


if __name__ == "__main__":

    X, y = load_breast_cancer(return_X_y=True)

    D = X.shape[1]
    X_train, X_test, y_train, y_test = train_test_split(
        X, y, test_size=0.3, random_state=0)
    n_train, n_test = X_train.shape[0], X_test.shape[0]

    spark = SparkSession\
        .builder\
        .appName("Logistic Regression")\
        .getOrCreate()

    matrix = np.concatenate(
        [X_train, np.ones((n_train, 1)), y_train.reshape(-1, 1)], axis=1)

    points = spark.sparkContext.parallelize(matrix, n_slices).cache()

    # Initialize w to a random value
    w = 2 * np.random.ranf(size=D + 1) - 1
    print("Initial w: " + str(w))

    for t in range(n_iterations):
        print("On iteration %d" % (t + 1))
        g = points.map(lambda point: gradient(point, w)).reduce(add)
        w -= alpha * g

        y_pred = logistic_f(np.concatenate(
            [X_test, np.ones((n_test, 1))], axis=1), w)
        pred_label = np.where(y_pred < 0.5, 0, 1)
        acc = accuracy_score(y_test, pred_label)
        print("iterations: %d, accuracy: %f" % (t, acc))

    print("Final w: %s " % w)
    print("Final acc: %f" % acc)

    spark.stop()

注意spark.sparkContext.parallelize(matrix, n_slices)中的n_slices就是Spark中的分割區數。我們在程式碼中採用breast cancer資料集進行訓練和測試，該資料集是個二分類資料集。模型初始權重採用隨機初始化。

最後，我們來看一下演演算法的輸出結果。

初始權重如下：

Initial w: [-0.0575882   0.79680833  0.96928013  0.98983501 -0.59487909 -0.23279241
 -0.34157571  0.93084048 -0.10126002  0.19124314  0.7163746  -0.49597826
 -0.50197367  0.81784642  0.96319482  0.06248513 -0.46138666  0.76500396
  0.30422518 -0.21588114 -0.90260279 -0.07102884 -0.98577817 -0.09454256
  0.07157487  0.9879555   0.36608845 -0.9740067   0.69620032 -0.97704433
 -0.30932467]

最終的模型權重與在測試集上的準確率結果如下：

Final w: [ 8.22414803e+02  1.48384087e+03  4.97062125e+03  4.47845441e+03
  7.71390166e+00  1.21510016e+00 -7.67338147e+00 -2.54147183e+00
  1.55496346e+01  6.52930570e+00  2.02480712e+00  1.09860082e+02
 -8.82480263e+00 -2.32991671e+03  1.61742379e+00  8.57741145e-01
  1.30270454e-01  1.16399854e+00  2.09101988e+00  5.30845885e-02
  8.28547658e+02  1.90597805e+03  4.93391021e+03 -4.69112527e+03
  1.10030574e+01  1.49957834e+00 -1.02290791e+01 -3.11020744e+00
  2.37012097e+01  5.97116694e+00  1.03680530e+02] 
Final acc: 0.923977

可見我們的演演算法收斂良好。

參考