SSE影象演演算法優化系列三十二：Zhang\Guo影象細化演演算法的C語言以及SIMD指令優化

二值影象的細化演演算法也有很多種，比較有名的比如Hilditch細化、Rosenfeld細化、基於索引表的細化、還有Opencv自帶的THINNING_ZHANGSUEN、THINNING_GUOHALL喜歡等等。這些都屬於迭代的細化方式，當然還有一種是基於二值影象距離變換的細化方法，二值想比較，我個人認為是基於迭代的效果穩定、可靠，但是速度較慢，且速度和圖片的內容有關，基於距離變換的版本，優點是速度穩定，但是效果差強人意。本文這裡還是選擇基於迭代的方式予以實現。

相關的參考文章有：http://cgm.cs.mcgill.ca/~godfried/teaching/projects97/azar/skeleton.html Hilditch細化

　　　　　　　　　　http://www.cnblogs.com/xiaotie/archive/2010/08/12/1797760.html 對Hilditch細化的改進版

　　　　　　　　　 http://cgm.cs.mcgill.ca/~godfried/teaching/projects97/azar/skeleton.html Rosenfeld細化

　　　　　　　　　　 https://github.com/opencv/opencv_contrib/blob/4.x/modules/ximgproc/src/thinning.cpp　　　　Opencv的Zhang\guo細化

　　我們嘗試的看下了Hilditch細化以及改進版本的Hilditch細化演演算法，發現其在某一個行的計算過程中，有著嚴重的前後依賴，非常不利於SIMD指令的並行化，這裡我們優化了Opencv的兩個運算元。

　 一、原始方案

在上述的Opencv程式碼的連結中，以Zhang細化演演算法為例，其核心程式碼如下所示：

  if(thinningType == THINNING_ZHANGSUEN){
        for (int i = 1; i < img.rows-1; i++)
        {
            for (int j = 1; j < img.cols-1; j++)
            {
                uchar p2 = img.at<uchar>(i-1, j);
                uchar p3 = img.at<uchar>(i-1, j+1);
                uchar p4 = img.at<uchar>(i, j+1);
                uchar p5 = img.at<uchar>(i+1, j+1);
                uchar p6 = img.at<uchar>(i+1, j);
                uchar p7 = img.at<uchar>(i+1, j-1);
                uchar p8 = img.at<uchar>(i, j-1);
                uchar p9 = img.at<uchar>(i-1, j-1);

                int A  = (p2 == 0 && p3 == 1) + (p3 == 0 && p4 == 1) +
                         (p4 == 0 && p5 == 1) + (p5 == 0 && p6 == 1) +
                         (p6 == 0 && p7 == 1) + (p7 == 0 && p8 == 1) +
                         (p8 == 0 && p9 == 1) + (p9 == 0 && p2 == 1);
                int B  = p2 + p3 + p4 + p5 + p6 + p7 + p8 + p9;
                int m1 = iter == 0 ? (p2 * p4 * p6) : (p2 * p4 * p8);
                int m2 = iter == 0 ? (p4 * p6 * p8) : (p2 * p6 * p8);

                if (A == 1 && (B >= 2 && B <= 6) && m1 == 0 && m2 == 0)
                    marker.at<uchar>(i,j) = 1;
            }
        }
    }

　　非常之簡潔啊，簡潔的沒有朋友，也沒有效率的。這樣的程式碼其實只適合於新手學習演演算法的原理。無法用於實際的專案的。

　　可以明顯的看出，A\B\m1\m2的判斷並不要放在一起，而是可以分開，分開的話在很多的情況下後續的計算就可以不用做了，要知道，這是一個迭代的演演算法，而且通常要迭代幾百次，因此，每一個迭代裡能少一次計算量，整體下來的時間是非常可觀的。

　　二、稍微改進版本

　　我們稍微做一個脫離Opencv版本的程式碼版本：

int IM_Thinning_Zhangsuen_PureC(unsigned char *Src, unsigned char *Dest, int Width, int Height, int Stride)
{
    int Channel = Stride / Width;
    if ((Src == NULL) || (Dest == NULL))                return IM_STATUS_NULLREFRENCE;
    if ((Width <= 0) || (Height <= 0))                    return IM_STATUS_INVALIDPARAMETER;
    if (Channel != 1)                                    return IM_STATUS_INVALIDPARAMETER;
    int Status = IM_STATUS_OK;
    const int MaxIter = 2000;

    unsigned char *Clone = (unsigned char *)calloc((Height + 2) * (Width + 2), sizeof(unsigned char));
    unsigned short *IndexX = (unsigned short *)malloc(Width * Height / 4 * sizeof(unsigned short));
    unsigned short *IndexY = (unsigned short *)malloc(Width * Height / 4 * sizeof(unsigned short));
    if ((Clone == NULL) || (IndexX == NULL) || (IndexY == NULL))
    {
        Status = IM_STATUS_OUTOFMEMORY;
        goto FreeMemory;
    }

    for (int Y = 0; Y < Height; Y++)
    {
        unsigned char *LinePS = Src + Y * Stride;
        unsigned char *LinePD = Clone + (Y + 1) * (Width + 2) + 1;
        for (int X = 0; X < Width; X++)
        {
            LinePD[X] = LinePS[X] & 1;        //    全部量化為0和1兩個數值
        }
    }
    int Iter = 0;
    while (true)
    {
        int Amount = 0;
        for (int Y = 0; Y < Height; Y++)
        {
            unsigned char *LinePF = Clone + Y * (Width + 2) + 1;
            unsigned char *LinePS = Clone + (Y + 1) * (Width + 2) + 1;
            unsigned char *LinePT = Clone + (Y + 2) * (Width + 2) + 1;
            for (int X = 0; X < Width; X++)
            {
                int P1 = LinePS[X];
                if (P1 == 0)    continue;            
                // P9 P2 P3
                // P8 P1 P4
                // P7 P6 P5
                //
                //int P9 = LinePF[X - 1];
                //int P2 = LinePF[X];
                //int P3 = LinePF[X + 1];
                //int P8 = LinePS[X - 1];
                //int P4 = LinePS[X + 1];
                //int P7 = LinePT[X - 1];                    
                //int P6 = LinePT[X];
                //int P5 = LinePT[X + 1];
                //int Sum = P2 + P3 + P4 + P5 + P6 + P7 + P8 + P9;
                //if ((Sum < 2) || (Sum > 6)) continue;                            

                int P2 = LinePF[X];
                int P8 = LinePS[X - 1];
                int P4 = LinePS[X + 1];            
                int P6 = LinePT[X];
                int Sum = P2 + P8 + P4 + P6;
                if (Sum == 4) continue;                             
                int P3 = LinePF[X + 1];
                int P9 = LinePF[X - 1];
                int P5 = LinePT[X + 1];
                int P7 = LinePT[X - 1];                    
                Sum += P3 + P5 + P7 + P9;
                if (Sum < 2) continue;                             

                int Count = 0;
                
                if ((P2 == 0) && (P3 == 1))        Count++;
                if ((P3 == 0) && (P4 == 1))        Count++;
                if ((P4 == 0) && (P5 == 1))        Count++;
                if ((P5 == 0) && (P6 == 1))        Count++;
                if ((P6 == 0) && (P7 == 1))        Count++;
                if ((P7 == 0) && (P8 == 1))        Count++;
                if ((P8 == 0) && (P9 == 1))        Count++;
                if ((P9 == 0) && (P2 == 1))        Count++;

                if ((Count == 1) && ((P2 & P4 & P6) == 0) && ((P4 & P6 & P8) == 0))
                {
                    IndexX[Amount] = X;
                    IndexY[Amount] = Y;
                    Amount++;
                }
            }
        }

        if (Amount == 0) break;
        for (int Y = 0; Y < Amount; Y++)
        {
            Clone[(IndexY[Y] + 1) * (Width + 2) + IndexX[Y] + 1] = 0;
        }
   
        Amount = 0;
        for (int Y = 0; Y < Height; Y++)
        {
        　　//　　後續的第二次迴圈，僅僅是幾個變數判斷不一樣，自行新增
        }
        if (Amount == 0)    break;
        for (int Y = 0; Y < Amount; Y++)
        {
            Clone[(IndexY[Y] + 1) * (Width + 2) + IndexX[Y] + 1] = 0;
        }
        Iter++;
        if (Iter >= MaxIter)    break;
    }
    for (int Y = 0; Y < Height; Y++)
    {
        unsigned char *LinePD = Dest + Y * Stride;
        unsigned char *LinePS = Clone + (Y + 1) * (Width + 2) + 1;

        for (int X = 0; X < Width; X++)
        {
            LinePD[X] = LinePS[X] == 1 ? 255 : 0;
        }
    }
FreeMemory:
    if (Clone != NULL)         free(Clone);
    if (IndexX != NULL)        free(IndexX);
    if (IndexY != NULL)        free(IndexY);
    return Status;
}

　　幾個方面的改進和改動：

1、使用了一個擴充套件邊界的影象（高度和寬度在四周各擴散一個畫素，類似於哨兵邊界），用於減少每次取3*3領域時的邊界判斷。這個雖然佔用了記憶體，但是可以很大的提高速度。

2、把A1\B\M的判斷分開寫，這樣可以讓有些迴圈提前退出，提高速度。

3、沒有使用Vector，直接使用陣列儲存哪些需要改變值的位置（因為計算量小，對速度基本沒有影響）。

4、對B的判斷分了2步走，可以稍微提高下速度。

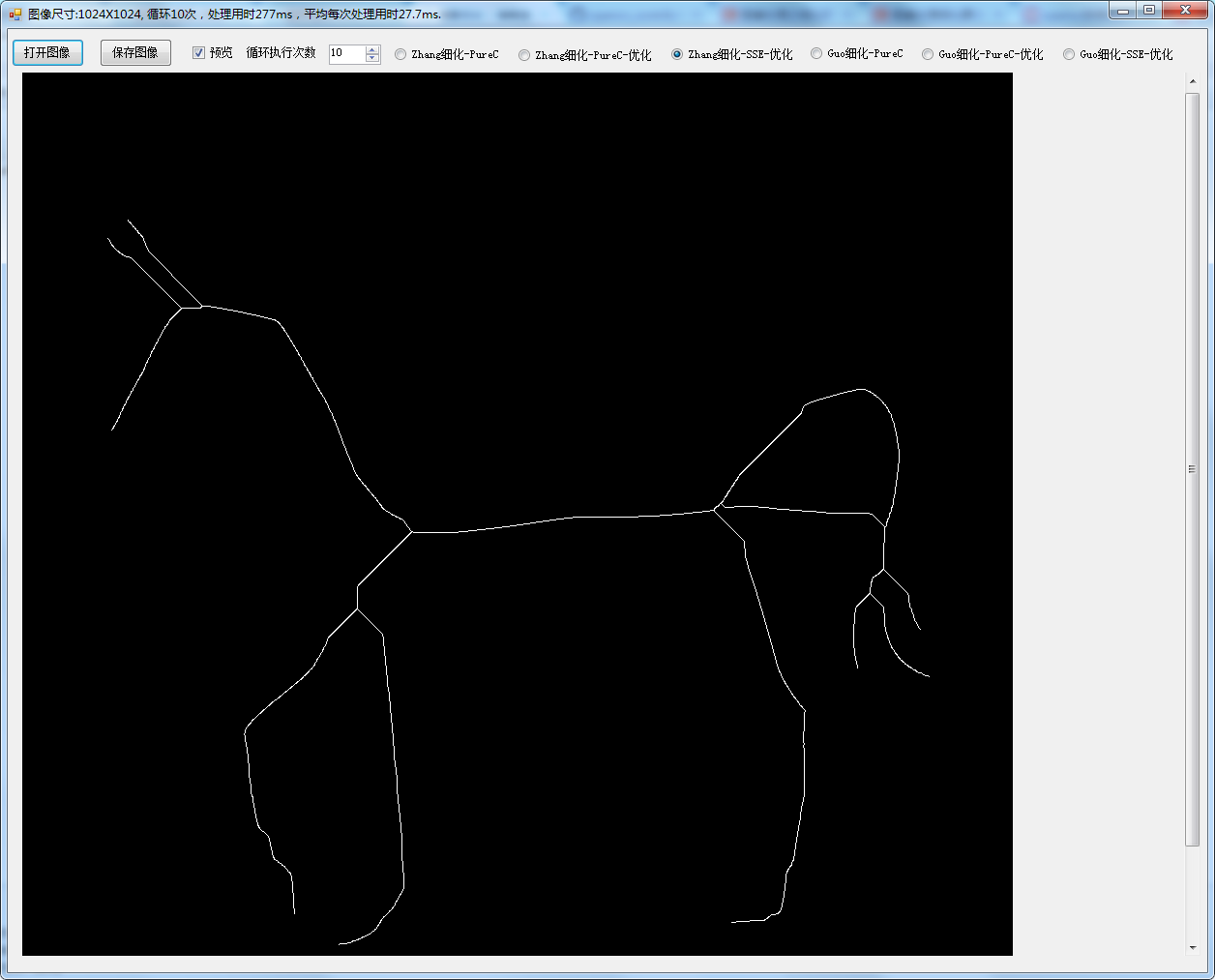
　　我們選擇下面這個測試圖：

　　一副1024*1024大小的測試圖，在我本機上上述測試程式碼的平均耗時大約是180ms，這個速度談不上快。

　　三、再次改進版本

在我們進行SIMD優化前，我們還嘗試了從演演算法層面上的另外一種優化。

　　我們知道，在細化的演演算法中，本身已經是背景的畫素是不要參與計算的，也就是上述程式碼中if (P1 == 0) continue; 的含義，那麼如果沒在迭代前，就算好了哪些部位不要計算，是不是迭代後就可以直接計算那些需要計算部分呢，這樣就可以少了很多判斷，雖然只是一個判斷，但是在全圖裡如果有50%是背景，那就意味著要進行W*H/2判斷的，再加上這個是在迭代裡進行判斷，計算量也是相當可觀的。

　　這個事先計算好哪些是前景的工作，針對二值影象，其實就是類似於傳統的RLE行程編碼，我們計算出每行前景的起點終點，等等。這個演演算法大家自行去研究。

　　如果在每次迭代前都進行這個RLE行程編碼，那也會帶來新的問題，因為行程編碼也是全圖處理，也是一個需要時間的工作，那這樣後續帶來的速度優化反而會被行程編碼給抵消甚至導致減速。但是，如果只進行迭代前的一次編碼，隨著迭代的進行，更多的畫素被判定為背景，之前計算的行程編碼裡已經有很多是不需要計算的了，為了解決這個矛盾，一個建議的處理方法就是，每個若干次迭代，更新下行程編碼的結果，比如20次或者50次，這樣的話，即不會因為行程編碼的耗時影響整體速度，又在一定程度上逐次的減少了計算量。

　　相關程式碼如下所示：

int IM_Thinning_Zhangsuen_PureC_Opt(unsigned char *Src, unsigned char *Dest, int Width, int Height, int Stride)
{
    int Channel = Stride / Width;
    if ((Src == NULL) || (Dest == NULL))                return IM_STATUS_NULLREFRENCE;
    if ((Width <= 0) || (Height <= 0))                    return IM_STATUS_INVALIDPARAMETER;
    if (Channel != 1)                                     return IM_STATUS_INVALIDPARAMETER;
    int Status = IM_STATUS_OK;
    const int MaxIter = 2000;

    unsigned char *Clone = (unsigned char *)calloc((Height + 2) * (Width + 2), sizeof(unsigned char));
    unsigned short *IndexX = (unsigned short *)malloc(Width * Height / 4 * sizeof(unsigned short));
    unsigned short *IndexY = (unsigned short *)malloc(Width * Height / 4 * sizeof(unsigned short));
    RLE_Line *RL_H = (RLE_Line *)malloc((Height + 2) * sizeof(RLE_Line));

    if ((Clone == NULL) || (IndexX == NULL) || (IndexY == NULL) || (RL_H == NULL))
    {
        Status = IM_STATUS_OUTOFMEMORY;
        goto FreeMemory;
    }

    for (int Y = 0; Y < Height; Y++)
    {
        unsigned char *LinePS = Src + Y * Stride;
        unsigned char *LinePD = Clone + (Y + 1) * (Width + 2) + 1;
        for (int X = 0; X < Width; X++)
        {
            LinePD[X] = LinePS[X] & 1;
        }
    }
    Status = IM_GetMaskRLE_Hori(Clone, Width + 2, Height + 2, Width + 2, RL_H);
    if (Status != IM_STATUS_OK)    goto FreeMemory;
    int Iter = 0;
    while (true)
    {
        if (Iter % 50 == 0)    //    每迭代50次更細一下
        {
            for (int Z = 0; Z < Height + 2; Z++)
            {
                if ((RL_H[Z].Amount != 0) && (RL_H[Z].SE != NULL))    free(RL_H[Z].SE);
            }
            Status = IM_GetMaskRLE_Hori(Clone, Width + 2, Height + 2, Width + 2, RL_H);
        }
        int Amount = 0;
        for (int Y = 0; Y < Height; Y++)
        {
            unsigned char *LinePF = Clone + Y * (Width + 2) + 1;
            unsigned char *LinePS = Clone + (Y + 1) * (Width + 2) + 1;
            unsigned char *LinePT = Clone + (Y + 2) * (Width + 2) + 1;
            for (int K = 0; K < RL_H[Y + 1].Amount; K++)
            {
                for (int X = RL_H[Y + 1].SE[K].Start - 1 ; X <= RL_H[Y + 1].SE[K].End - 1; X++)
                {
                    int P1 = LinePS[X];
                    if (P1 == 0)    continue;
                    // P9 P2 P3
                    // P8 P1 P4
                    // P7 P6 P5                          // 條件3：至少有兩個是前景點

                    int P2 = LinePF[X];
                    int P8 = LinePS[X - 1];
                    int P4 = LinePS[X + 1];
                    int P6 = LinePT[X];
                    int Sum = P2 + P8 + P4 + P6;
                    if (Sum == 4) continue;                             // 條件2： P1,P3,P5,P7不全部為前景點
                    int P3 = LinePF[X + 1];
                    int P9 = LinePF[X - 1];
                    int P5 = LinePT[X + 1];
                    int P7 = LinePT[X - 1];                    // 以方便計算8連通聯結數。
                    Sum += P3 + P5 + P7 + P9;
                    if (Sum < 2) continue;                              // 條件3：至少有兩個是前景點

                    int Count = 0;

                    if ((P2 == 0) && (P3 == 1))        Count++;
                    if ((P3 == 0) && (P4 == 1))        Count++;
                    if ((P4 == 0) && (P5 == 1))        Count++;
                    if ((P5 == 0) && (P6 == 1))        Count++;
                    if ((P6 == 0) && (P7 == 1))        Count++;
                    if ((P7 == 0) && (P8 == 1))        Count++;
                    if ((P8 == 0) && (P9 == 1))        Count++;
                    if ((P9 == 0) && (P2 == 1))        Count++;

                    if ((Count == 1) && ((P2 & P4 & P6) == 0) && ((P4 & P6 & P8) == 0))
                    {
                        IndexX[Amount] = X;
                        IndexY[Amount] = Y;
                        Amount++;
                    }
                }
            }
        }
        if (Amount == 0) break;
        for (int Y = 0; Y < Amount; Y++)
        {
            Clone[(IndexY[Y] + 1) * (Width + 2) + IndexX[Y] + 1] = 0;
        }
        Amount = 0;
        for (int Y = 0; Y < Height; Y++)
        {
           　//　後續的第二次迴圈，自行新增
        }
        if (Amount == 0) break;
        for (int Y = 0; Y < Amount; Y++)
        {
            Clone[(IndexY[Y] + 1) * (Width + 2) + IndexX[Y] + 1] = 0;
        }
        Iter++;
        if (Iter >= MaxIter)    break;
    }
    for (int Y = 0; Y < Height; Y++)
    {
        unsigned char *LinePD = Dest + Y * Stride;
        unsigned char *LinePS = Clone + (Y + 1) * (Width + 2) + 1;

        for (int X = 0; X < Width; X++)
        {
            LinePD[X] = LinePS[X] == 1 ? 255 : 0;
        }
    }
FreeMemory:
    if (Clone != NULL)        free(Clone);
    if (IndexX != NULL)        free(IndexX);
    if (IndexY != NULL)        free(IndexY);
    if (RL_H != NULL)
    {
        for (int Z = 0; Z < Height + 2; Z++)
        {
            if ((RL_H[Z].Amount != 0) && (RL_H[Z].SE != NULL))    free(RL_H[Z].SE);
        }
        free(RL_H);
    }
    return Status;
}

　　同樣的影象，速度可以提高到55ms,有將近3倍額速度提高。

　　不過這裡的提速比例不是很固定的，對於不同的型別的影象結果不禁相同，對於那些有大塊連續的二值圖，提速就越明顯，而對於毫無規律的隨機圖，可能就不是很明顯了。

　　四、SSE改進版本

　上述改進版本還可以通過SIMD指令進一步優化，類似於我在Sobel優化裡使用的方法，我們一次性載入16個位元組以及他周邊的8個位置連續的16個位元組，但是核心的技巧在於如何實現那些分支預測，特別是continue。

　　因為一次性載入了16個畫素，在利用了行程編碼後，案例說這16個位元組都是需要進行處理的目標，但是由於前述不是每次迭代都要更新行程編碼的緣故，總會有部分是無效畫素，也有可能是全部的無效畫素，因此，我們處理的程式碼中就可能同時存在前景和背景，但是對於背景我們是不需要處理的，而前景畫素也有可能在中間條件判斷時退出迴圈，但是對於SIMD質量來說，他無法區域性退出，要麼大家一起計算，要麼大家一起退出，因此，我們必須將須有的計算都完成，而不能提前退出，但是有一點特殊的就是，如果所有的畫素都已經滿足了某個提提前退出的條件，那也是可以退出的。

因為我們知道，在每次迭代時，對於前景中哪些大塊的範圍，其中間的區域都是不滿足要改變的條件的，也就是說在上面的 if (Sum == 4) continue; if (Sum < 2) continue; 就滿足了退出條件，因此利用SIMD一次性就可以做16次判斷和計算。這樣也可以提高速度。

    __m128i P1 = _mm_loadu_si128((__m128i *)(LinePS + X));
    __m128i FlagA = _mm_cmpeq_epi8(P1, _mm_setzero_si128());            //    全部為0，退出
    if (_mm_movemask_epi8(FlagA) == 65535)    continue;

    __m128i Flag = _mm_andnot_si128(FlagA, _mm_set1_epi8(255));            //    記錄下那些是不為0的

    __m128i P2 = _mm_loadu_si128((__m128i *)(LinePF + X + 0));
    __m128i P8 = _mm_loadu_si128((__m128i *)(LinePS + X - 1));
    __m128i P4 = _mm_loadu_si128((__m128i *)(LinePS + X + 1));
    __m128i P6 = _mm_loadu_si128((__m128i *)(LinePT + X + 0));

    __m128i Sum = _mm_add_epi8(_mm_add_epi8(P2, P4), _mm_add_epi8(P6, P8));
    __m128i FlagB = _mm_cmpeq_epi8(Sum, _mm_set1_epi8(4));
    if (_mm_movemask_epi8(FlagB) == 65535)    continue;                    //    全部都等於4，退出
    Flag = _mm_andnot_si128(FlagB, Flag);                                //    記錄下那些不為0，且Sum不等於4的

    __m128i P9 = _mm_loadu_si128((__m128i *)(LinePF + X - 1));
    __m128i P3 = _mm_loadu_si128((__m128i *)(LinePF + X + 1));
    __m128i P7 = _mm_loadu_si128((__m128i *)(LinePT + X - 1));
    __m128i P5 = _mm_loadu_si128((__m128i *)(LinePT + X + 1));

    Sum = _mm_add_epi8(Sum, _mm_add_epi8(_mm_add_epi8(P9, P3), _mm_add_epi8(P7, P5)));
    __m128i FlagC = _mm_cmplt_epi8(Sum, _mm_set1_epi8(2));
    if (_mm_movemask_epi8(FlagC) == 65535)    continue;                    //    全部都小於2，退出
    Flag = _mm_andnot_si128(FlagC, Flag);                                //    記錄下那些不為0，且Sum不等於4的，後續的Sum小於2的

    __m128i Count = _mm_setzero_si128();

    Count = _mm_sub_epi8(Count, _mm_and_si128(_mm_cmpeq_epi8(P2, Zero), _mm_cmpeq_epi8(P3, One)));
    Count = _mm_sub_epi8(Count, _mm_and_si128(_mm_cmpeq_epi8(P3, Zero), _mm_cmpeq_epi8(P4, One)));
    Count = _mm_sub_epi8(Count, _mm_and_si128(_mm_cmpeq_epi8(P4, Zero), _mm_cmpeq_epi8(P5, One)));
    Count = _mm_sub_epi8(Count, _mm_and_si128(_mm_cmpeq_epi8(P5, Zero), _mm_cmpeq_epi8(P6, One)));
    Count = _mm_sub_epi8(Count, _mm_and_si128(_mm_cmpeq_epi8(P6, Zero), _mm_cmpeq_epi8(P7, One)));
    Count = _mm_sub_epi8(Count, _mm_and_si128(_mm_cmpeq_epi8(P7, Zero), _mm_cmpeq_epi8(P8, One)));
    Count = _mm_sub_epi8(Count, _mm_and_si128(_mm_cmpeq_epi8(P8, Zero), _mm_cmpeq_epi8(P9, One)));
    Count = _mm_sub_epi8(Count, _mm_and_si128(_mm_cmpeq_epi8(P9, Zero), _mm_cmpeq_epi8(P2, One)));

    __m128i P246 = _mm_and_si128(_mm_and_si128(P2, P4), P6);
    __m128i P468 = _mm_and_si128(_mm_and_si128(P4, P6), P8);

    __m128i FlagD = _mm_and_si128(_mm_cmpeq_epi8(Count, One), _mm_and_si128(_mm_cmpeq_epi8(P246, Zero), _mm_cmpeq_epi8(P468, Zero)));
    if (_mm_movemask_epi8(FlagD) == 0)    continue;

    Flag = _mm_and_si128(FlagD, Flag);

    //    用Flag.m128i_u8或者寫入到一個臨時陣列裡速度沒啥區別
    if (_mm_extract_epi8(Flag, 0) == 255)
    {
        IndexX[Amount] = X + 0;
        IndexY[Amount] = Y;
        Amount++;
    }

    if (_mm_extract_epi8(Flag, 1) == 255)
    {
        IndexX[Amount] = X + 1;
        IndexY[Amount] = Y;
        Amount++;
    }

      /////////////////////////////////////////////////
////////////////////////////////////////////////////////////////

　　上面的細節有幾個地方值的學習。

　　第一、_mm_movemask_epi8的使用，這個我在很多場合下都提過，可用於批次判斷一個SIMD暫存器裡的狀態。本例只用他做判斷是否SSE暫存器都符合某一個指標。

第二、Flag 變數的作用，Flag用於來記錄下滿足所有條件的畫素，這樣才能知道經過多個判斷後最終還剩下那些畫素需要真正的處理。其中_mm_andnot_si128也是一個靈活的應用。

　　第三、if ((P2 == 0) && (P3 == 1)) Count++; 這樣的語句如果直接翻譯到SSE程式碼，是比較麻煩的（可以使用_mm_blendv_si128），我這裡巧妙的使用了u8和i8資料型別的特點，u8的255就對應了i8的-1，0還是對應0，然後加法就可以變為減法了。

　第四、填寫IndeX和IndexY的過程確實是無法用SIMD指令實現的，這裡只能去拆解SIMD變數，這個有幾個方法，一個就是用想本例中直接使用_mm_extract_epi8，另外一種方式可以是使用SIMD變數的m128i_u8成員，但是這個有可能對效能有所影響。

　　使用SIMD優化後，上述相同的圖片大概耗時在28ms左右，速度有進一步的提高。

　　五、其他說明

　　雖然較原始版本速度有較大的提高，但是和商業軟體相比，還是有很大的差距，人家halcon這個圖用時5ms，直接悲劇。

　　至少目前從公開的資料中還沒有看到halcon所用的演演算法的為什麼這麼快，待有緣了在研究這個演演算法吧。

　　另外，halcon的計算結果和opencv的GulHALL的結果比較類似，但是那個演演算法要比Zhang還要慢。

　　當然，CV自帶的這兩個演演算法是可以並行的，當然這裡的必行是指迭代內部的並行，而不是迭代之間的並行，但是由於每次迭代的計算量相對於來說比較小，這種並行對CPU級別的執行緒來說是不太划算的，但是GPU級別的還是很友好的。不過HALONC這個演演算法可沒有用GPU哦。

　　測試Demo: Zhang 以及 Guo 影象細化

如果想時刻關注本人的最新文章，也可關注公眾號或者新增本人微信： laviewpbt