關於基礎RMQ——ST演演算法

RMQ，Range Maximum/Minimum Query，顧名思義，就是詢問某個區間內的最大值或最小值，今天我主要記錄的是其求解方法——ST演演算法

相對於線段樹，它的執行速度會快很多，可以做到O(log n)的預處理和O(1)的查詢，不足就是無法進行區間修改，這個一會就會提及

我將從四個方面進行記錄：

1、ST的演演算法流程

其實與DP有很大的相似性，用 a[1,2,....,n] 來記錄整組資料，設 f[i,j] 代表從 a[i] 到 a[i+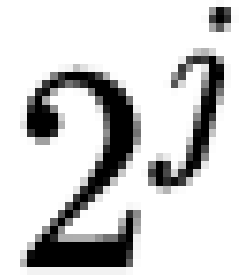-1] 之間所有元素的最大值。

不難發現，其實這個區間就有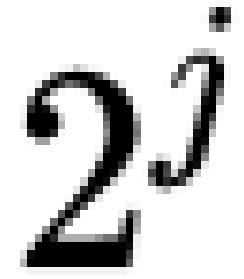個元素。現在我們將這些元素平均分為兩部分，那麼每部分就是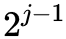個元素，而這兩個集合就可以寫成：

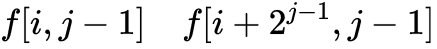
那麼整個區間的最大值就轉換成了兩個區間最大值的較大值，根據動態規劃的最佳化原理，就可以輕鬆的寫出狀態轉移方程：

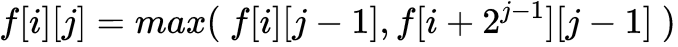
邊界條件就是：

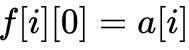
2、詢問

要想要找出區間 [x,y] 的最大值，與剛才講的方法類似，找出最大的 a 滿足：

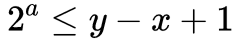
至於為啥不能是直接取等於，是因為取等於時不一定是整數。

所以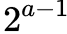不一定是正好是整個區間的一半，會出現以下這種情況：

不過That's OK，因為就算區間有重疊也不會影響最大值的確定，但是如果進行區間的操作的話可能就不適用了，因為重疊的部分會被操作兩次，這明顯不公平！這也是我最開始的時候對ST進行批判的原因，也是ST演演算法只適用於求區間最值的原因。

3、程式碼實現

剛才其實都講的差不多了，不做過多解釋：

 1 #include<cstdio>
 2 #include<cmath>
 3 #include<iostream>
 4 #include<algorithm>
 5 using namespace std;
 6 const int NN=1e6+5;
 7 int f[NN][21];//21位就差不多了，2的21次方超過了1e6 
 8 
 9 inline int read()//快讀 
10 {
11     char ha=getchar();
12     int x=0,sign=1;
13     while(ha<'0'||ha>'9')
14     {
15         if(ha=='-')
16         {
17             sign=-1;
18         }
19         ha=getchar();
20     }
21     while(ha>='0'&&ha<='9')
22     {
23         x=x*10+ha-'0';
24         ha=getchar();
25     }
26     return x*sign;
27 }
28 
29 int Query(int l,int r)
30 {
31     int logg=log2(r-l+1); 
32     int haha=max(f[l][logg],f[r-(1<<logg)+1][logg]);
33     return haha; 
34 }
35 int main()
36 {
37     int N=read(),M=read();
38     for(int i=1;i<=N;i++)//初始化，只有一個數的區間最大值就是它本身 
39     {
40         f[i][0]=read();
41     }
42     for(int j=1;j<=21;j++)//開始DP找最大值 
43     {
44         for(int i=1;i+(1<<j)-1<=N;i++)
45         {
46             f[i][j]=max(f[i][j-1],f[i+(1<<(j-1))][j-1]);
47         }
48     }
49     for(int i=1;i<=M;i++)
50     {
51         int l=read(),r=read();
52         int ans=Query(l,r);
53         printf("%d\n",ans);
54     }
55     return 0;
56 }

四、例題精講

敬請期待！

To Be Continued...