【自動微分原理】自動微分的具體實現

第一篇自動微分原理文章中我們大概初步談了談從手動微分到自動微分的過程，第二篇自動微分正反模式中深入了自動微分的正反向模式具體公式和推導。

實際上第二章瞭解到正反向模式只是自動微分的原理模式，在實際程式碼實現的過程，正方向模式只是提供一個原理性的指導，在真正編碼過程會有很多細節需要開啟，例如如何解析表示式，如何記錄反向求導表示式的操作等等。這一篇文章中，ZOMI希望通過介紹目前比較熱門的方法給大家普及一下自動微分的具體實現。

• 【自動微分原理】01. 原理介紹
• 【自動微分原理】02. 正反模式
• 【自動微分原理】03. 具體實現

自動微分實現

瞭解自動微分的不同實現方式非常有用。在這裡呢，我們將介紹主要的自動微分實現方法。在上一篇的文章中，我們介紹了自動微分的基本數學原理。可以總結自動微分的關鍵步驟為：

• 分解程式為一系列已知微分規則的基礎表示式的組合
• 根據已知微分規則給出各基礎表示式的微分結果
• 根據基礎表示式間的資料依賴關係，使用鏈式法則將微分結果組合完成程式的微分結果

雖然自動微分的數學原理已經明確，包括正向和反向的數學邏輯和模式。但具體的實現方法則可以有很大的差異，2018 年，Siskind 等學者在其綜述論文Automatic Differentiation in Machine Learning: a Survey [1] 中對自動微分實現方案劃分為三類：

基本表示式：基本表示式或者稱元素庫（Elemental Libraries），基於元素庫中封裝一系列基本的表示式（如：加減乘除等）及其對應的微分結果表示式，作為庫函數。使用者通過呼叫庫函數構建需要被微分的程式。而封裝後的庫函數在執行時會記錄所有的基本表示式和相應的組合關係，最後使用鏈式法則對上述基本表示式的微分結果進行組合完成自動微分。

操作符過載：操作符過載或者稱運算過載（Operator Overloading，OO），利用現代語言的多型特性（例如C++/JAVA/Python等高階語言），使用操作符過載對語言中基本運算表示式的微分規則進行封裝。同樣，過載後的操作符在執行時會記錄所有的操作符和相應的組合關係，最後使用鏈式法則對上述基本表示式的微分結果進行組合完成自動微分。

原始碼變換：原始碼變換或者叫做原始碼轉換（Source Code Transformation，SCT）則是通過對語言前處理器、編譯器或直譯器的擴充套件，將其中程式表達（如：原始碼、AST抽象語法樹 或 編譯過程中的中間表達 IR）的基本表示式微分規則進行預定義，再對程式表達進行分析得到基本表示式的組合關係，最後使用鏈式法則對上述基本表示式的微分結果進行組合生成對應微分結果的新程式表達，完成自動微分。

任何 AD 實現中的一個主要考慮因素是 AD 運算時候引入的效能開銷。就計算複雜性而言，AD 需要保證算術量增加不超過一個小的常數因子。另一方面，如果不小心管理 AD 演演算法，可能會帶來很大的開銷。例如，簡單的分配資料結構來儲存對偶數（正向運算和反向求導），將涉及每個算術運算的記憶體存取和分配，這通常比現代計算機上的算術運算更昂貴。同樣，使用運運算元過載可能會引入伴隨成本的方法分派，與原始函數的原始數值計算相比，這很容易導致一個數量級的減速。

下面這個圖是論文作者回顧了一些比較通用的 AD 實現。

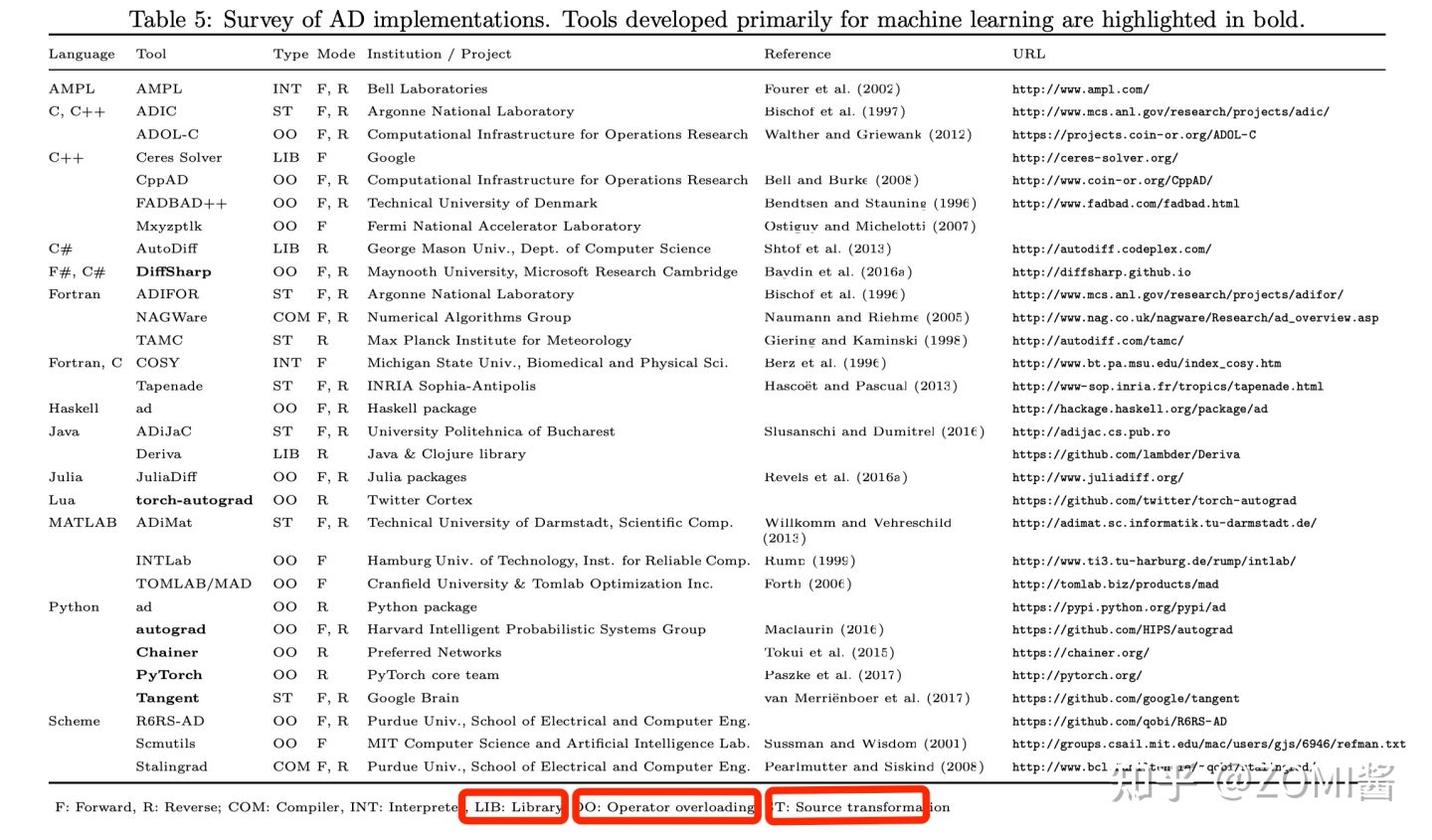
基本表示式

基本表示式法也叫做元素庫（Elemental Libraries），程式中實現構成自動微分中計算的最基本的類別或者表示式，並通過呼叫自動微分中的庫，來代替數學邏輯運算來工作。然後在函數定義中使用庫公開的方法，這意味著在編寫程式碼時，手動將任何函數分解為基本操作。

這個方法呢從自動微分剛出現的時候就已經被廣泛地使用，典型的例子是 Lawson (1971) 的 WCOMP 和 UCOMP 庫，Neidinger (1989) 的 APL 庫，以及 Hinkins (1994) 的工作。同樣，Rich 和 Hill (1992) 使用基本表示式法在 MATLAB 中制定了他們的自動微分實現。

以公式為例子：

使用者首先需要手動將公式1中的各個操作，或者叫做子函數，分解為庫函數中基本表示式組合：

t1 = log(x)
t3 = sin(x)
t2 = x1 * x2
t4 = x1 + x2
t5 = x1 - x2

使用給定的庫函數，完成上述函數的程式設計：

// 引數為變數 x,y,t 和對應的導數變數 dx,dy,dt
def ADAdd(x, y, dx, dy, t, dt)

// 同理對上面的公式實現對應的函數
def ADSub(x, y, dx, dy, t, dt)
def ADMul(x, y, dx, dy, t, dt)
def ADLog(x, dx, t, dt)
def ADSin(x, dx, t, dt)

而庫函數中則定義了對應表示式的數學微分規則，和對應的鏈式法則:

// 引數為變數 x,y,t 和對應的導數變數 dx,dy,dt
def ADAdd(x, y, dx, dy, t, dt):
    t = x + y
    dt = dy + dx

// 引數為變數 x,y,t 和對應的導數變數 dx,dy,dt
def ADSub(x, y, dx, dy, t, dt):
    t = x - y
    dt = dy - dx

// ... 以此類推

針對公式1中基本表示式法，可以按照下面範例程式碼來實現正向的推理功能，反向其實也是一樣，不過呼叫程式碼更復雜一點：

x1 = xxx
x2 = xxx
t1 = ADlog(x1)
t2 = ADSin(x2)
t3 = ADMul(x1, x2)
t4 = ADAdd(t1, t3)
t5 = ADSub(t4, t2)

基本表示式法的優點可以總結如下：

• 實現簡單，基本可在任意語言中快速地實現為庫

基本表示式法的缺點可以總結如下：

• 使用者必須使用庫函數進行程式設計，而無法使用語言原生的運算表示式；
• 另外實現邏輯和程式碼也會冗餘較長，依賴於開發人員較強的數學背景

基本表示式法在沒有操作符過載AD的80到90年代初期，仍然是計算機中實現自動微分功能最簡單和快捷的策略啦。

操作符過載

在具有多型特性的現代程式語言中，運運算元過載提供了實現自動微分的最直接方式，利用了程式語言的第一特性（first class feature），重新定義了微分基本操作語意的能力。

在 C++ 中使用運運算元過載實現的流行工具是 ADOL-C（Walther 和 Griewank，2012）。 ADOL-C 要求對變數使用啟用 AD 的型別，並在 Tape 資料結構中記錄變數的算術運算，隨後可以在反向模式 AD 計算期間「回放」。 Mxyzptlk 庫 (Michelotti, 1990) 是 C++ 能夠通過前向傳播計算任意階偏導數的另一個例子。 FADBAD++ 庫（Bendtsen 和 Stauning，1996 年）使用模板和運運算元過載為 C++ 實現自動微分。對於 Python 語言來說，autograd 提供正向和反向模式自動微分，支援高階導數。

在機器學習 ML 或者深度學習 DL 領域，目前AI框架中使用操作符過載的一個典型代表是 Pytroch，其中使用資料結構 Tape 來記錄計算流程，在反向模式求解梯度的過程中進行replay Operator。

1. 操作符過載來實現自動微分的功能裡面，很重要的是利用高階語言的特性。下面簡單看看虛擬碼，這裡面我們定義一個特殊的資料結構 Variable，然後基於 Variable 過載一系列的操作如 __mul__ 代替 * 操作。

class Variable:
    def __init__(self, value):
        self.value = value

    def __mul__(self, other):
        return ops_mul(self, other)

   # 同樣過載各種不同的基礎操作
   def __add__(self, other)
   def __sub__(self, other)
   def __div__(self, other)

1. 實現操作符過載後的計算。

def ops_mul(self, other):
    x = Variable(self.value * other.value)

1. 接著通過一個 Tape 的資料結構，來記錄每次 Variable
   執行計算的順序，Tape 這裡面主要是記錄正向的計算，把輸入、輸出和執行運算的操作符記錄下來。

class Tape(NamedTuple):
    inputs : []
    outputs : []
    propagate : (inputs, outpus)

1. 因為大部分 ML 系統或者 AI 框架採用的是反向模式，因此最後會逆向遍歷 Tape 裡面的資料（相當於反向傳播或者反向模式的過程），然後累積反向計算的梯度。

# 反向求導的過程，類似於 Pytroch 的 backward 介面
def grad(l, results):

    # 通過 reversed 操作把帶有梯度資訊的 tape 逆向遍歷
    for entry in reversed(gradient_tape):
        # 進行梯度累積，反向傳播給上一次的操作計算
        dl_d[input] += dl_dinput

當然啦，我們會在下一節當中帶著大家親自通過操作符過載實現一個前向的自動微分和後向的自動微分。下面總結一下操作符過載的一個基本流程：

• 預定義了特定的資料結構，並對該資料結構過載了相應的基本運算操作符
• 程式在實際執行時會將相應表示式的操作型別和輸入輸出資訊記錄至特殊資料結構
• 得到特殊資料結構後，將對資料結構進行遍歷並對其中記錄的基本運算操作進行微分
• 把結果通過鏈式法則進行組合，完成自動微分

操作符過載法的優點可以總結如下：

• 實現簡單，只要求語言提供多型的特效能力
• 易用性高，過載操作符後跟使用原生語言的程式設計方式類似

操作符過載法的缺點可以總結如下：

• 需要顯式的構造特殊資料結構和對特殊資料結構進行大量讀寫、遍歷操作，這些額外資料結構和操作的引入不利於高階微分的實現
• 對於一些類似 if，while 等控制流表示式，難以通過操作符過載進行微分規則定義。對於這些操作的處理會退化成基本表示式方法中特定函數封裝的方式，難以使用語言原生的控制流表示式

原始碼轉換

原始碼轉換（Source Code Transformation，SCT）是最複雜的，實現起來也是非常具有挑戰性。

原始碼轉換的實現提供了對程式語言的擴充套件，可自動將演演算法分解為支援自動微分的基本操作。通常作為前處理器執行，以將擴充套件語言的輸入轉換為原始語言。簡單來說就是利用源語言來實現領域擴充套件語言 DSL 的操作方式。

原始碼轉換的經典範例包括 Fortran 前處理器 GRESS（Horwedel 等人，1988 年）和 PADRE2（Kubo 和 Iri，1990 年），在編譯之前將啟用 AD 的 Fortran 變體轉換為標準 Fortran。類似地，ADIFOR 工具 (Bischof et al., 1996) 給定一個 Fortran 原始碼，生成一個增強程式碼，其中除了原始結果之外還計算所有指定的偏導數。對於以 ANSI C 編碼的過程，ADIC 工具（Bischof 等人，1997）在指定因變數和自變數之後將 AD 實現為原始碼轉換。 Tapenade（Pascual 和 Hasco¨et，2008 年；Hasco¨et 和 Pascual，2013 年）是過去10年終 SCT 的流行工具，它為 Fortran 和 C 程式實現正向和反向模式 AD。

除了通過原始碼轉換進行語言擴充套件外，還有一些實現通過專用編譯器或直譯器引入了具有緊密整合的 AD 功能的新語言。一些最早的 AD 工具，例如 SLANG (Adamson and Winant, 1969) 和 PROSE (Pfeiffer, 1987) 屬於這一類。 NAGWare Fortran 編譯器 (Naumann and Riehme, 2005) 是一個較新的範例，其中使用與 AD 相關的擴充套件會在編譯時觸發衍生程式碼的自動生成。

作為基於直譯器的實現的一個例子，代數建模語言 AMPL (Fourer et al., 2002) 可以用數學符號表示目標和約束，系統從中推匯出活動變數並安排必要的 AD 計算。此類別中的其他範例包括基於類似 Algol 的 DIFALG 語言的 FM/FAD 包 (Mazourik, 1991)，以及類似於 Pascal 的物件導向的 COZY 語言 (Berz et al., 1996)。

而華為全場景AI框架 MindSpore 則是基於 Python 語言使用原始碼轉換實現 AD 的正反向模式，並採用了函數語言程式設計的風格，該機制可以用控制流表示複雜的組合。函數被轉換成函數中間表達（Intermediate Representation，IR），中間表達構造出一個能夠在不同裝置上解析和執行的計算圖。在執行前，計算圖上應用了多種軟硬體協同優化技術，以提升端、邊、雲等不同場景下的效能和效率。

其主要流程是：分析獲得源程式的 AST 表達形式；然後基於 AST 完成基本表示式的分解和微分操作；再通過遍歷 AST 得到基本表示式間的依賴關係，從而應用鏈式法則完成自動微分。

因為原始碼轉換涉及到底層的抽象語法樹、編譯執行等細節，因此這裡就不給出虛擬碼了（實在太難了給不出來），我們通過下面這張圖來簡單瞭解下 SCT 的一般性過程。

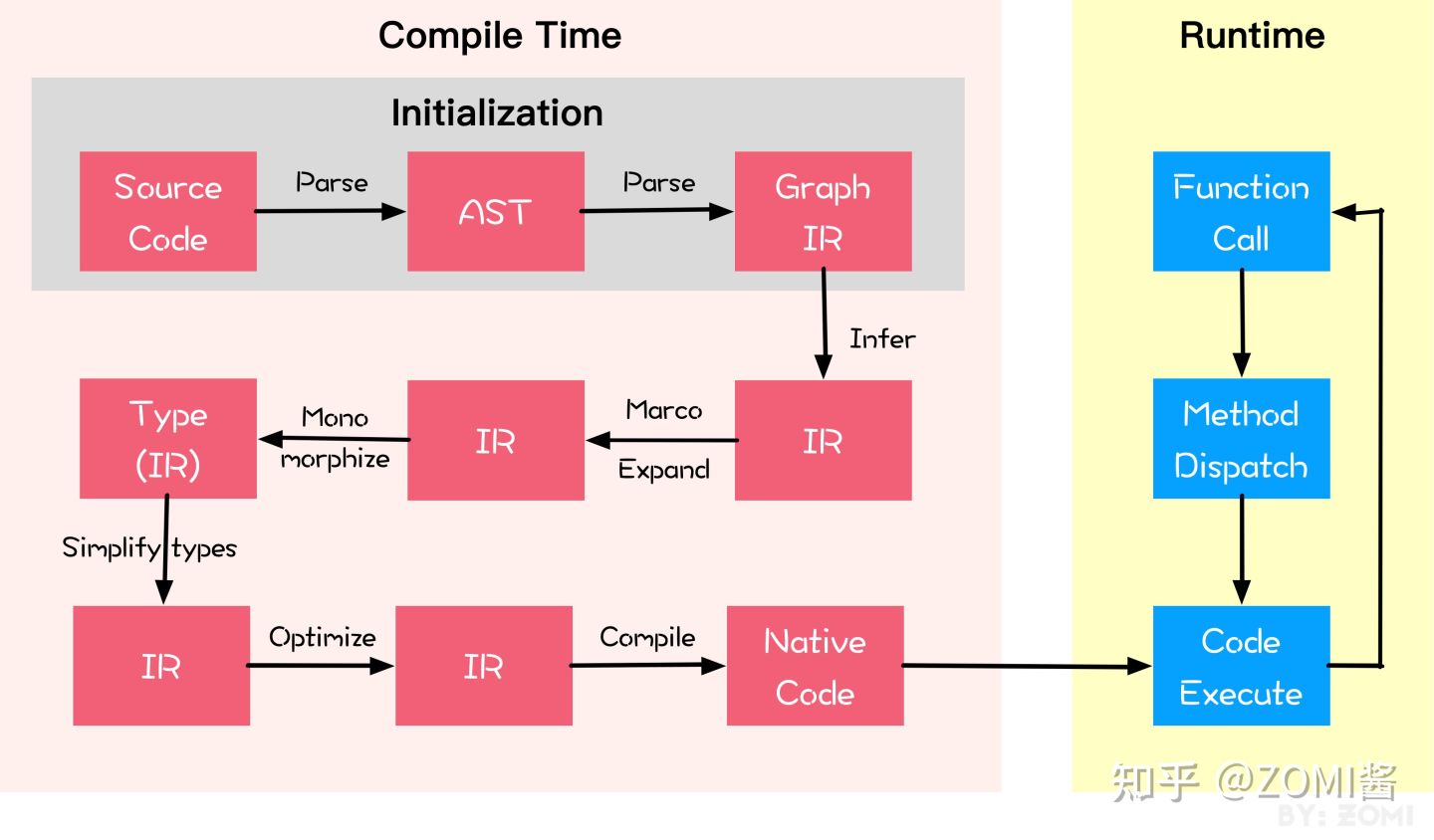
從圖中可以看到原始碼轉換的整體流程分為編譯時間和執行時間，以 MindSpore 為例，其在執行之前的第一個 epoch 會等待一段時間，是因為需要對原始碼進行編譯轉換解析等一系列的操作。然後再 run time 執行時則會比較順暢，直接對資料和程式碼不斷地按照計算機指令來高速執行。

編譯階段呢，在 Initialization 過程中會對原始碼進行 Parse 轉換成為抽象語法樹 AST，接著轉換為基於圖表示的中間表達 IR，這個基於圖的IR從概念上理解可以理解為計算圖，神經網路層數的表示通過圖表示會比較直觀。

接著對 Graph base IR進行一些初級的型別推導，特別是針對 Tensor/List/Str 等不同的基礎資料表示，然後進行宏展開，還有語言單態化，最後再對變數或者自變數進行型別推導。可以從圖中看到，很多地方出現了不同形式的 IR，IR 其實是編譯器中常用的一箇中間表達概念，在編譯的 Pass 中會有很多處理流程，每一步處理流程產生一個 IR，交給下一個Pass進行處理。

最後通過 LLVM 或者其他等不同的底層編譯器，最後把 IR 編譯成機器碼，然後就可以真正地在runtime執行起來。

原始碼轉換法的優點可以總結如下：

• 支援更多的資料型別（原生和使用者自定義的資料型別） + 原生語言操作（基本數學運算操作和控制流操作）
• 高階微分中實現容易，不用每次使用 Tape 來記錄高階的微分中產生的大量變數，而是統一通過編譯器進行額外變數優化和重計算等優化
• 進一步提升效能，沒有產生額外的 tape 資料結構和 tape 讀寫操作，除了利於實現高階微分以外，還能夠對計算表示式進行統一的編譯優化

原始碼轉換法的缺點可以總結如下：

• 實現複雜，需要擴充套件語言的前處理器、編譯器或直譯器，深入計算機體系和底層編譯
• 支援更多資料型別和操作，使用者自由度雖然更高，但同時更容易寫出不支援的程式碼導致錯誤
• 微分結果是以程式碼的形式存在，在執行計算的過程當中，特別是深度學習中大量使用for迴圈過程中間錯誤了，或者是資料處理流程中出現錯誤，並不利於深度偵錯

參考

[1] Automatic Differentiation in Machine Learning: a Survey: https://arxiv.org/abs/1502.05767

[2] Rirchard L. Burden and J. Douglas Faires. Numerical Analysis. Brooks/Cole, 2001.

[3] Max E. Jerrell. Automatic differentiation and interval arithmetic for estimation of disequilibrium models. Computational Economics, 10(3):295–316, 1997.

[4] Johannes Grabmeier and Erich Kaltofen. Computer Algebra Handbook: Foundations, Applications, Systems. Springer, 2003.

[5] G. W. Leibniz. Machina arithmetica in qua non additio tantum et subtractio sed et multiplicatio nullo, diviso vero paene nullo animi labore peragantur. Hannover, 1685.

[6] George F. Corliss. Application of differentiation arithmetic, volume 19 of Perspectives in Computing, pages 127–48. Academic Press, Boston, 1988.

[7] Arun Verma. An introduction to automatic differentiation. Current Science, 78(7):804–7, 2000.

[8] Andreas Griewank and Andrea Walther. Evaluating Derivatives: Principles and Techniques of Algorithmic Differentiation. Society for Industrial and Applied Mathematics, Philadelphia, 2008. doi: 10.1137/1.9780898717761.

[9] John F. Nolan. Analytical differentiation on a digital computer. Master’s thesis, Massachusetts Institute of Technology, 1953.

[10] L. M. Beda, L. N. Korolev, N. V. Sukkikh, and T. S. Frolova. Programs for automatic differentiation for the machine BESM (in Russian). Technical report, Institute for Precise Mechanics and Computation Techniques, Academy of Science, Moscow, USSR, 1959.

[11] Robert E. Wengert. A simple automatic derivative evaluation program. Communications of the ACM, 7:463–4, 1964.

[12] Andreas Griewank. On automatic differentiation. pages 83–108, 1989.

[13] Hascoet, Laurent, and Valérie Pascual. "The Tapenade automatic differentiation tool: principles, model, and specification." ACM Transactions on Mathematical Software (TOMS) 39.3 (2013): 1-43.

[14] 知乎專欄：自動微分（Automatic Differentiation）: https://zhuanlan.zhihu.com/p/61103504

[15] 知乎專欄：數值計算方法 第六章 數值積分和數值微分: https://zhuanlan.zhihu.com/p/14

[16] 知乎專欄：技術分享 | 從自動微分到可微程式語言設計 https://zhuanlan.zhihu.com/p/39