【工程應用七】接著折騰模板匹配演演算法 （Optimization選項 + no_pregeneration模擬 + 3D亞畫素插值）

　　在折騰中成長，在折騰中永生。

       接著玩模板匹配，最近主要研究了3個課題。

       1、建立模型的Optimization選項模擬（2022.5.16日）

　　這兩天又遇到一個做模板匹配隱藏的高手，切磋起來後面就還是和halcon比，於是有看了下create_shape_model這個函數，前面一直忙實現細節，對halcon的Optimization這個引數真的沒怎麼在意，幾天一看，原來這裡面還隱藏了比較深的細節。halcon原始的英文描述如下：

　　For particularly large models, it may be useful to reduce the number of model points by setting Optimization to a value different from 'none'. If Optimization = 'none', all model points are stored. In all other cases, the number of points is reduced according to the value of Optimization. If the number of points is reduced, it may be necessary in find_shape_model to set the parameter Greediness to a smaller value, e.g., 0.7 or 0.8. For small models, the reduction of the number of model points does not result in a speed-up of the search because in this case usually significantly more potential instances of the model must be examined. If Optimization is set to 'auto', create_shape_model automatically determines the reduction of the number of model points.

　　 Optionally, a second value can be passed in Optimization. This value determines whether the model is pregenerated completely or not. To do so, the second value of Optimization must be set to either 'pregeneration' or 'no_pregeneration'. If the second value is not used (i.e., if only one value is passed), the mode that is set with set_system('pregenerate_shape_models',...) is used. With the default value ('pregenerate_shape_models' = 'false'), the model is not pregenerated completely. The complete pregeneration of the model normally leads to slightly lower runtimes because the model does not need to be transformed at runtime. However, in this case, the memory requirements and the time required to create the model are significantly higher. It should also be noted that it cannot be expected that the two modes return exactly identical results because transforming the model at runtime necessarily leads to different internal data for the transformed models than pregenerating the transformed models. For example, if the model is not pregenerated completely, find_shape_model typically returns slightly lower scores, which may require setting a slightly lower value for MinScore than for a completely pregenerated model. Furthermore, the poses obtained by interpolation may differ slightly in the two modes. If maximum accuracy is desired, the pose of the model should be determined by least-squares adjustment.

　　翻譯成中文的核心意思是，對於大的模板影象，將改引數設定而為非"none"的其他值，可以降低匹配時需要的模型點的數量，從而提高速度，當然，如果模型點數量降低了，在呼叫find_shape_model 時最好把那個貪婪值稍微吊的小一點，比如改成0.7或者0.8，以便保證穩定性。當然，這個操作對於小模型可能作用不大。一般情況下，可以設定為"atuo"，這樣create_shape_model 自動絕對如何來降低取樣點數。

　　 另外，這個函數還可以有第二個型別的值和前面的模型點數量集合，即pregeneration和no_pregeneration選項，這個是關鍵。 預設情況是no_pregeneration，當選擇pregeneration時，create_shape_model就會和我現在的實現方式一樣，對每層金字塔以及金字塔內不同角度均計算特徵點資料，因此，這個建立函數就會比較慢和佔用大量的記憶體。但是帶來的好處就是find_shape_model函數可能執行時間會快一些。no_pregeneration選項只會計算未旋轉模板的相關資訊，在find_shape_model時候會對資訊進行轉換，因此建立時非常快。特別注意，兩個選項得到的匹配結果會有輕微的不同。比如說，如果使用no_pregeneration，find_shape_model 函數的得分可能要稍微低一點。 所以，我目前實現的相當於使用了pregeneration選項的halcon功能。

　　具體來說：optimization 有7種選項可以選擇

　　 List of values: 'auto', 'no_pregeneration', 'none', 'point_reduction_high', 'point_reduction_low', 'point_reduction_medium', 'pregeneration'

　　我們看到point_reduction相關的有point_reduction_high point_reduction_low point_reduction_medium選項，我在想內部肯定是某個固定的方式減少模型點數量，這個我們也可以模擬，比如分別取1/8,1/4,1/2等等，經過測試，這個在提高速度的同時，對結果的準確度和精度基本沒有什麼影響。

        2、no_pregeneration選項的模擬（2022.5.18日）

　　這個很早以前就已經在考慮了，目前已經有過幾種嘗試，均已失敗告終，記錄如下。

      （1）create_shape_model 只記錄每層金字塔未旋轉模板影象的模型點特徵和位置（整形位置），然後在find_shape_model 時，旋轉特徵點的座標，並且四捨五入位置座標，使用0度模型點特徵和這個座標位置的查詢圖中特徵做匹配。

      （2）create_shape_model 只記錄每層金字塔未旋轉模板影象的模型點特徵和位置（整形位置），然後在find_shape_model 時，旋轉特徵點的座標，使用0度模型點特徵和查詢圖中這個座標位置周邊的領域的雙線性插值中特徵做匹配。

      （3）create_shape_model 只記錄每層金字塔未旋轉模板影象的模型點特徵和位置（亞畫素特徵值和位置），然後在find_shape_model 時，旋轉特徵點的座標，使用0度模型點特徵和查詢圖中這個座標位置周邊的領域的雙線性插值中特徵做匹配。

 　　測試結果均會出現目標丟失，如下所示： 

 3、3D的亞畫素插值（2022.5.23）

　　最近在看一篇臺灣人開源的基於NCC的模板匹配程式碼，詳見：https://github.com/DennisLiu1993/Fastest_Image_Pattern_Matching，在其程式碼中看到3D（X座標，Y座標和角度）的亞畫素計算方法， 在後續和作者的溝通中，作者提供了該演演算法的論文出處。其詳細的推到過程見下圖：      

 　編碼上其實也很簡單，主要是一些矩陣的乘法、轉置和求逆等。 

　 他實際上就是在3*3*3的空間內擬合曲面，在編碼時，我們需要在初步求得的X和Y座標以及角度值3領域範圍內（X加減1，Y加減1，Angle加減AngleStep）計算出27個得分值後進行矩陣運算即可。

     其實我一直在找這方面的資料，終於找到了，本來希望能得到一個比以前的2D或1D亞畫素更為精確的結果，不過實際測試起來還是有點失望的。　 

     以一個我常用的測試圖中一個結果為例說明（使用基於邊緣的匹配演演算法）：

 　　　　　　不使用亞畫素時的結果　　　　　　　　　　　　　　　　　　　　　　使用3D亞畫素時的結果                                                            使用2D亞畫素時的結果

　　這個圖理論的準確得分應該是1，不過由於中間的浮點計算誤差，導致得分無限接近於1，因此在不使用亞畫素時得到的結果其實是精確值，當使用3D亞畫素後，我們看到了X和Y座標結果有了很大的偏移，這個明顯是錯誤的。

　　後面為了分析這個問題，我一直在查詢3D亞畫素插值的程式碼，以為是程式碼寫錯了，後面用同樣的資料，使用matlab計算，得到的結果也是一樣的，說明不是程式碼問題，於是我列印出了對應的27個點的得分，如下所示：

        Score　　X - 1　　　X　　　　X + 1    　　　　　　　X - 1　　　X　　　　X + 1　　　　　　　　    X - 1　　　X　　　　X + 1

　　Y - 1  　　0.9891　　0.9213　　0.7208　　　|　　　0.9274　　0.9720　　0.9080　　　　|　　　　0.9855　　0.9324　　0.7223

　　Y　　　　0.9579　　0.8836　　0.6884　　　|　　　0.9491　　0.9999　　0.9562　　　　|　　　　0.9522　　0.8850　　0.6925

　　Y + 1　　 0.8395　　0.7772　　0.6303　　   |　　　0.8922　　0.9662　　0.9717　　　　|　　　　0.7830　　0.7373　　0.5660

　　　　　　　　　Angle - AngleStep　　　　　　　　　　　　 　   Angle　　　　　　　　　　　　　　　　 Angle+ AngleStep

　　我們仔細的觀察資料，發現只有在角度為 Angle時，（X,Y）點的得分為環繞最大值，而在其他角度時，得分的中心感覺都有點向左上角偏移，因此3D插值後的結果也會向左上角偏移，計算結果是符合資料的特性的。

       後面想一想啊，基於邊緣的查詢啊和邊緣的位置有著非常緊密的關係，稍微旋轉一個角度，邊緣的位置就有可能有一兩個畫素的偏移，這樣就會導致得分又較為明顯的差異，出現這個情況應該是正常點的。

       後面我把基於NCC的用3D的亞畫素插值試了一下，結果就好很多了，這個也很正常，因為NCC的相似度計算是基於全圖的，旋轉一個角度後，有多個點作用於結果得分值。

       因此，個人最後還是認為，在基於邊緣的匹配中可以使用2D的亞畫素作用於X和Y座標，使用1D的亞畫素作用於角度。

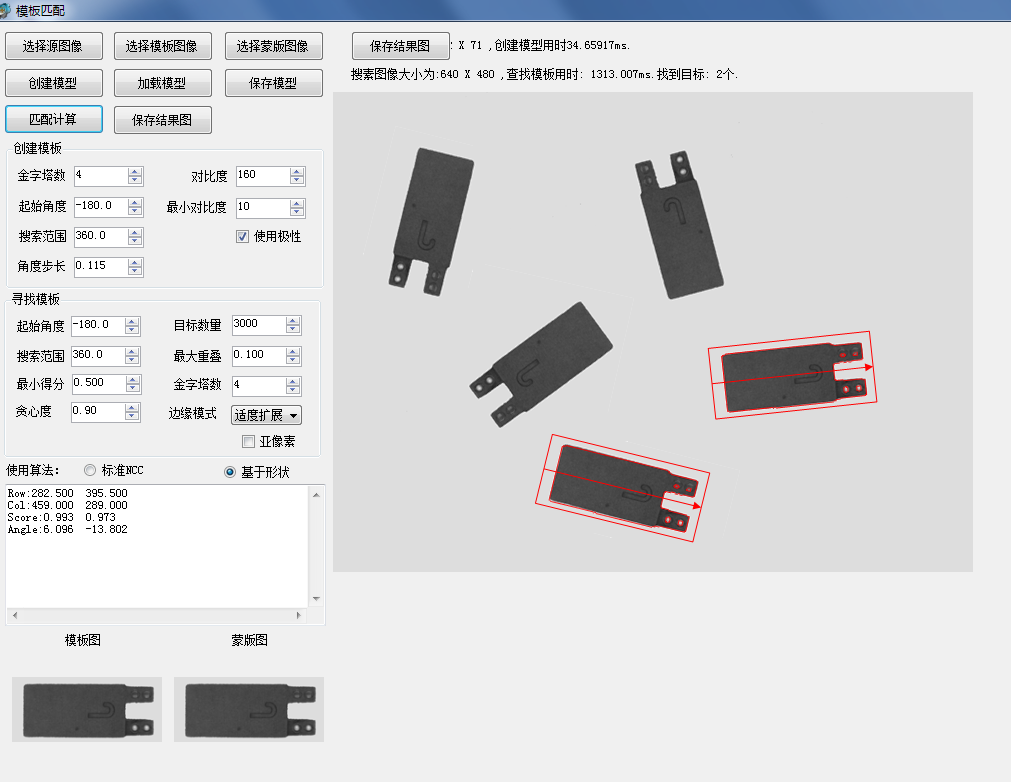
       最新版的一個測試DEMO: 帶蒙版的模板匹配。

       如果想時刻關注本人的最新文章，也可關注公眾號或者新增本人微信：  laviewpbt