TENSEAL: A LIBRARY FOR ENCRYPTED TENSOR OP- ERATIONS USING HOMOMORPHIC ENCRYPTION 解讀

本文記錄閱讀該paper的筆記，這篇論文是TenSeal庫的原理介紹。

摘要

機器學習演演算法已經取得了顯著的效果，並被廣泛應用於各個領域。這些演演算法通常依賴於敏感和私有資料，如醫療和財務記錄。因此，進一步關注隱私威脅和應用於機器學習模型的相應防禦技術至關重要。在本文中，我們介紹了TenSEAL，這是一個使用同態加密保護隱私資料的機器學習開源庫，可以輕鬆地整合到流行的機器學習框架（PyTorch 或 Tensorflow）中。我們使用MNIST資料集對我們的實現進行了benchmark測試，結果顯示加密的折積神經網路可以在不到一秒鐘的時間內進行計算，通訊量不到1/2MB。

介紹

近年來，機器學習狂奔發展。在典型場景中，使用者需要將資料傳送給服務提供商，服務提供商將對資料執行一些計算並返回結果。

這種方法有兩個關鍵問題。首先，出於隱私考慮，使用者可能不想將其資料傳送給服務提供商。其次，如果使用者不向服務提供商傳送資料，那服務提供商就無法向用戶提供模型。使用同態加密，可以解決該問題，使用者的資料將始終加密，服務提供商將看不到輸入和輸出，並且仍然可以對這些加密資料進行計算。

然而，在機器學習中採用同態加密的速度很慢。問題一：雖然目前可用的密碼庫為密碼學家提供了一個優秀的API，但它們可能會對資料科學家使用就不方便了（觸及密碼專業知識）。問題二：是計算成本，包括通訊和計算成本。

本文工作

提供了一個靈活的開源庫，使用同態加密進行張量計算（tensor computation）。該庫可以直接將當前流行機器學習框架（如PyTorch或Tensorflow）中的張量轉換為加密所支援的明文形式。

對於本文的其餘部分，第2節中描述該庫的體系結構。然後在第3節，詳細介紹了在加密空間中計算折積神經網路所需的演演算法。在第5節中對我們的庫進行了實驗性測試，並在第6節總結了我們工作的一些侷限性。

文章結構

TenSEAL是一個連線經典機器學習框架和同態加密功能的庫。它實現了在加密資料上進行張量計算。TenSEAL依賴於Microsoft SEAL庫。使用者端可以計算明文或加密的張量（支援C++或Python）。在客戶機-伺服器場景中，訊息交換是使用協定緩衝區完成的。核心API主要元件構建：環境（context）、明文張量（PlainTensor）和密文張量（Encrypted Tensor）計算。

環境（context）

TenSEAL的context是庫的核心元件，它生成並儲存金鑰（用於解密的私鑰、用於加密的公鑰、用於旋轉的伽羅瓦金鑰以及用於密文重新線性化的重新線性化金鑰）。這個物件還將處理執行緒池，執行緒池控制在執行可並行化操作時應並行執行的作業數。另外在context中可以設定自動密文重新線性化（relinearization）和重新縮放（rescaling ）。

明文張量（PlainTensor）

張量（Tensor）

Tensor是深度學習中廣泛使用的資料結構，本質上就是一個高維的矩陣，甚至將其理解為NumPy中array，Pandas中的DataFrame。

單個元素叫標量（scalar），一個序列叫向量（vector），多個序列組成的平面叫矩陣（matrix），多個平面組成的立方體叫張量（tensor）。在深度學習的範疇內，標量、向量和矩陣都統稱為張量。

參考：
1、PyTorch學習系列教學：何為Tensor？

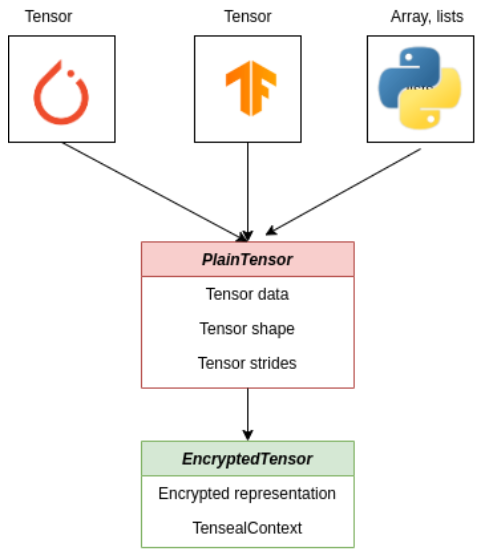
該圖顯示了密文張量的構建，PlainTensor封裝了當前流行框架中的張量表示，並用EncryptedTensor介面的輸入。

PlainTensor是一個將未加密的張量連線到加密實現的類。

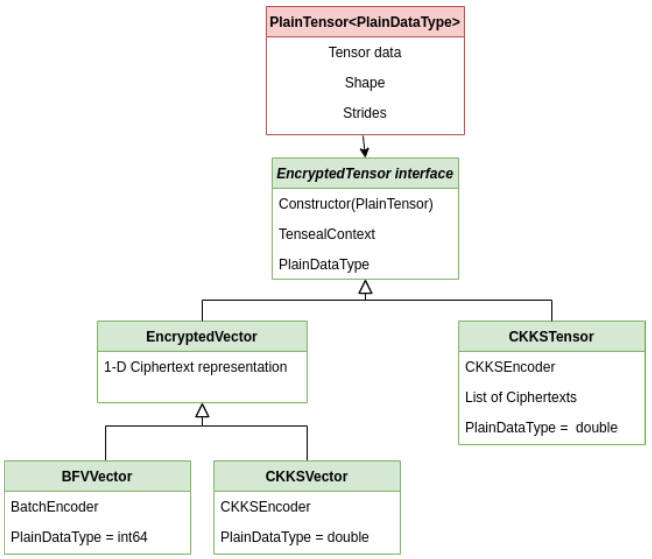
這顯示了張量的關係。EncryptedTensor介面派生為BFVVector、CKKVector或CKKSTensor類。

密文張量（Encrypted Tensor）

EncryptedSensor介面提供了一個API，該API需要由庫公開的每個張量來實現。介面有一個TenSEALContext物件，這是進行任何同態計算所必需的。派生類公開了不同的張量風格，例如：

CKKSVector派生EncryptedVector介面，可以將實數向量加密為單個密文。
CKKSTensor將的N維實數張量加密為的N維密文張量。然而，在對密文批次處理時，需要一個軸（axis），因此只需要（N-1）維密文張量。

方法

在同態加密方案上構建張量時，需要解決兩個重要問題：
1，如何在加密之前對張量進行編碼？
2、使用特定編碼時可以執行哪些操作？

CKKS方案的批次處理功能允許將N×N矩陣加密為N維密文向量，每行或每列作為一個密文。另一種可能性是將整個張量（N×N矩陣）加密為一個密文【paper：Secure outsourced matrix compu- tation and application to neural networks】。根據我們如何將明文張量放入密文中，我們可以用執行不同的操作（不同的複雜度）。目標是使用最小數量的密文，並以最小的執行時間獲得最大的深度，從而優化記憶體和計算。為了實現這一理想目標，我們發現可以將輸入影象進行加密為單個密文，並在折積神經網路上對其進行計算。這需要使用者端上的預處理步驟將影象編碼為矩陣，由折積視窗作為行組成，然後通過垂直掃描將其展平為向量。在TenSEAL中，所有這些功能都是圍繞CKKSVector實現的。CKKSVector包含N/2個實數，其中N是模多項式的次數。我們可以使用其他密文或者明文向量執行逐元素計算（加法、減法和乘法）。我們有一種計算加密向量次冪的方法，該方法使用最佳電路，從而使用最小乘法深度。此外，由於我們需要近似計算多項式，對於不同的啟用函數，我們構建了一種以加密向量為變數的多項式求值的方法，確保使用最小電路。除了元素操作之外，我們還需要矩陣操作來執行機器學習任務。我們實現了密文向量乘明文矩陣【paper：Algorithms in helib】，它可以使用多執行緒來更快地執行。下面是該庫的密文張量支援的操作：

點積（dot product）

該庫為點積提供計算方法【類似：Algorithms in helib】，但支援的向量大小不是2的冪，或者不能填充密文的所有插槽。前一種方法中的這種限制是由於向右旋轉（希望最後一個元素是第一個元素），這對於我們所處理的情況來說是不正確的。如果向量大小不是2的冪，我們的方法僅限於特定數量的點積。然而，由於方案允許的乘法次數可能較低，因此通常無法達到此限制。所以通過儘可能多次將輸入向量複製到密文槽中，並且在計算過程中只有密文左旋轉，該方法和【Algorithms in helib】有相同的演演算法複雜性。我們使用【CKKS17】中的方法實現了密文向量與明文矩陣之間的點積。因此，它可以擴充套件到支援密文矩陣與明文矩陣之間的點積（矩陣乘法）。下圖顯示瞭如何在加密向量和普通矩陣之間執行點積：

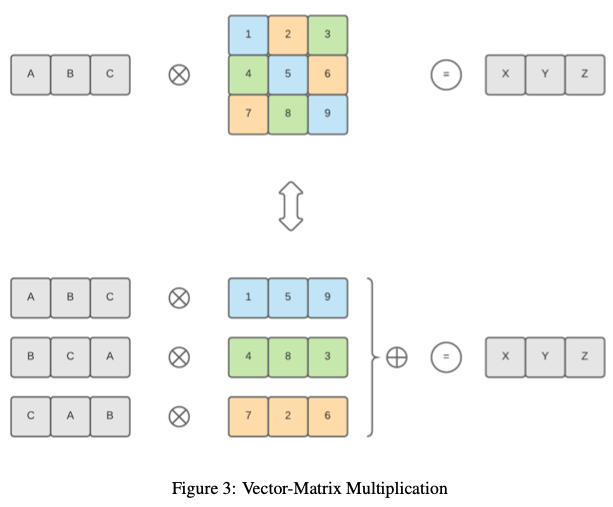
2維折積

折積

折積是一種數學運算，對兩個函數（訊號）的乘積進行積分，其中一個訊號翻轉。
下面我們將兩個訊號折積\(x =(0,1,2,3,4),w =(1,-1,2)\)：
（1）首先是將W水平翻轉（或向左旋轉180度）

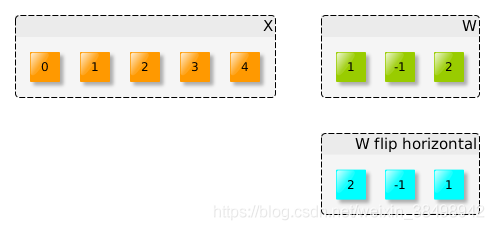
（2）需要將翻轉的W滑過輸入X：

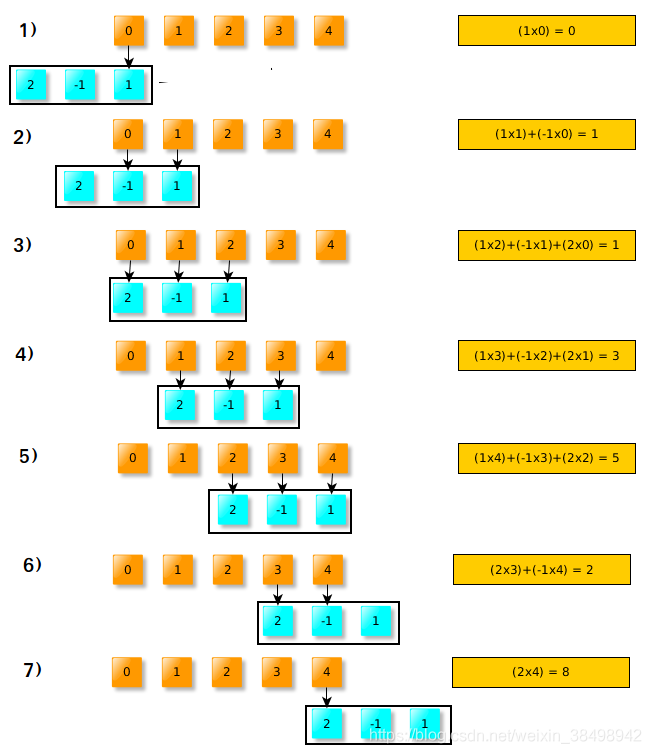
其中，在步驟3、4、5上，翻轉的視窗完全位於輸入訊號內。這些結果稱為「有效」折積。如果翻轉的視窗未完全位於輸入視窗（X）內，則可以考慮為零，或計算可能計算出的值，例如在第1步中，我們將1乘以零，其餘的將被忽略。

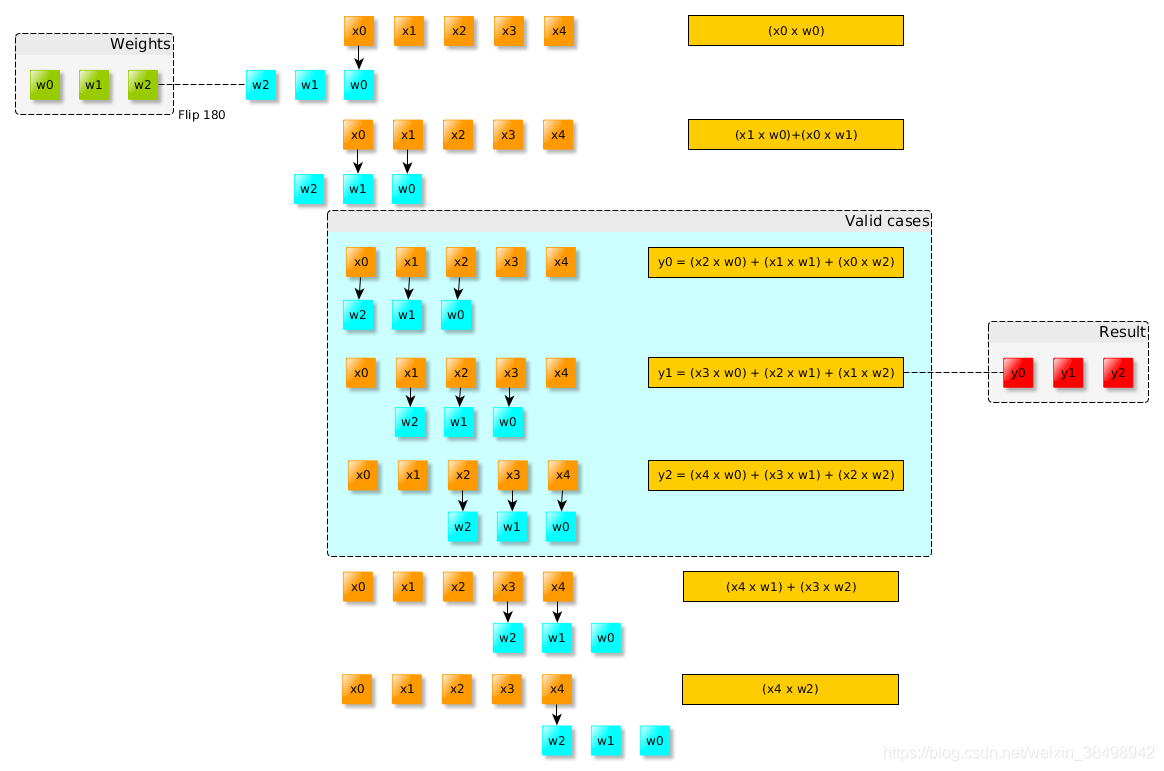
參考：
1、深度 | 理解深度學習中的折積

2D convolution

二維折積可以使用單個矩陣乘法來執行，而不是在每個視窗上重複乘法。這種方法稱為影象塊到列的折積（ image block to column），或影象到列的折積（image to column）。下圖顯示瞭如何使用此方法執行折積。它首先將輸入矩陣重新組織成表示折積視窗的行，然後用flattened kernel執行點積。

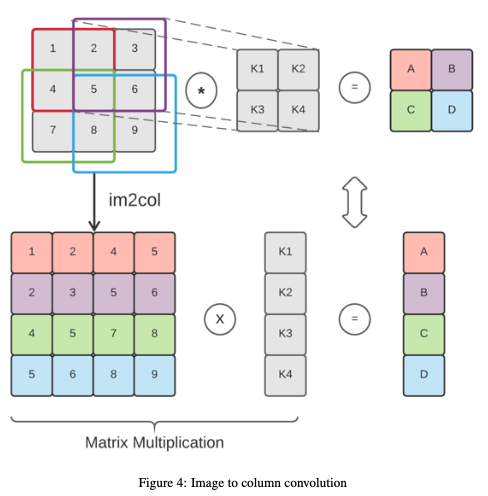
將此技術應用於加密矩陣（加密為一個密文）並不是一件小事，因為重新組織slot並不簡單。我們需要在加密之前將矩陣重新組織為預處理步驟，以便為折積做好準備。明文向量（kernel）和密文矩陣（輸入影象）的計算可以通過逐元素乘法和一系列旋轉和累加來執行。下圖顯示了執行此操作的步驟。第一個顯示了密文矩陣（彩色）是如何編碼並與明文向量（kernel）相乘的。第二步是對向左旋轉不同的不同版本的輸出求和。

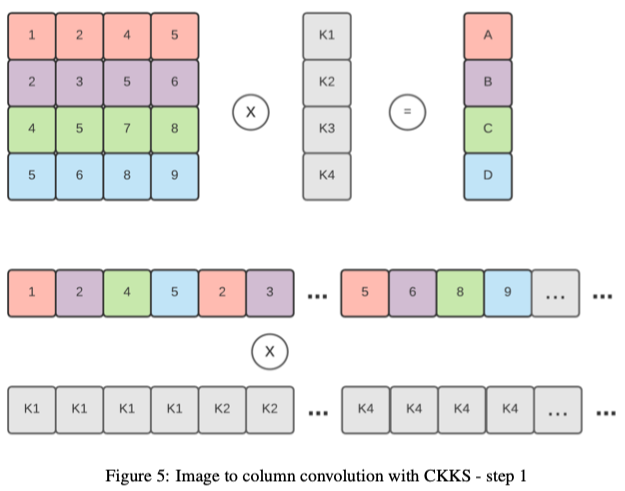
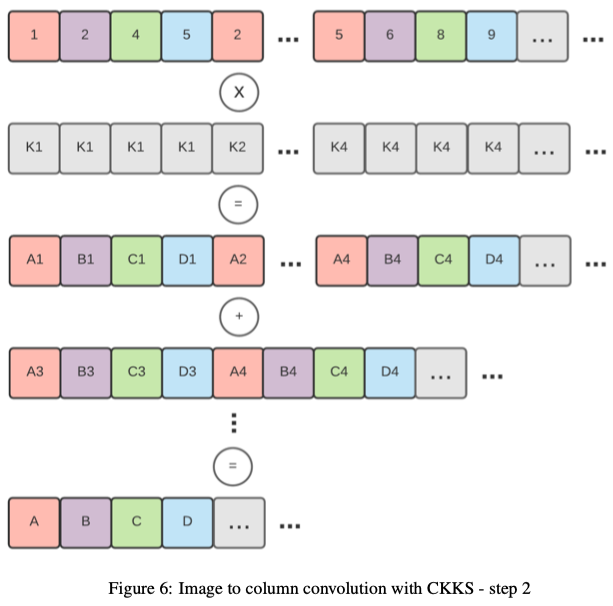
TenSEAL還支援計算折積，即提供當前流行的機器學習框架（例如PyTorch）計算折積的類似實現。我們將影象塊應用於Columns (im2col)【paper：Cnns in practice】，將折積層轉換為單個矩陣乘法運算。這種技術需要密文矩陣乘明文向量，我們通過複製的明文向量和轉置的矩陣逐元素向乘來實現。最後，將結果旋轉並累加到單個密文向量中。

此操作僅使用一個乘法運算和\(log2(N)\)個旋轉和加法，其中N表示矩陣中的行數。下面解釋瞭如何將「影象塊-》列」演演算法應用於加密輸入。需要注意的是，轉換髮生在明文資料中，轉換後的輸入影象進行編碼和加密為單個密文。這直接意味著堆疊兩個折積是不可能的，因為重新組織密文的slot並不簡單。

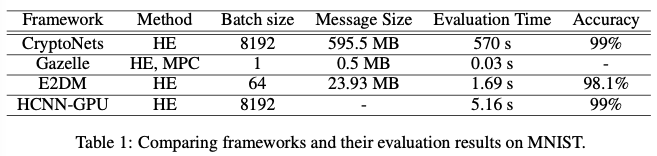
測試

為了測試我們的庫和技術，我們實現了一個由以下部分組成的神經網路：折積層（4個7x7的核心，步長為3x3）、線性層（輸入：256，輸出：64）和最終線性層（輸入：64，輸出：10）。除最後一層外，我們在每一層後使用平方啟用函數。折積是使用我們的影象-》列實現完成的，而線性層使用點積實現。明文測試集的準確率為97.7%，而密文測試集的準確率為97.4%。我們使用了CKKSVector實現，它使用CKKS方案。知道我們需要6次乘法計算和128位元的安全級別，我們將模多項式的級數（N）設定為8192，係數模數為206位，縮放因子（scale）為21位。測試是在Ubuntu伺服器20.04和Python 3.8上使用AWS c4完成的。2xlarge（8個VCPU）和AWS c4。4XL（16個VCPU）設定。測試的持續時間是5輪測試的平均值，每輪10次迭代。下表包含了在從MNIST資料集取樣的加密影象上計算神經網路的完整細分。

上表是測試MNIST計算的完整說明，持續時間以毫秒錶示。我們使用兩種設定來測試這些方法：Amazon c4。2xlarge範例（8個VCPU，15個GiB記憶體）和Amazon c4。4xlarge範例（16個VCPU，30 GiB記憶體），強調該庫並行性優秀。

結果表明，該庫大量實現並行，在網路通訊方面具有很強的競爭力，只需427KB的通訊即可傳送加密的輸入和接收加密的輸出。同時，TenSEAL沒有強行定義批次處理的大小（batch size），這使得它非常實用。完整的benchmarks測試是開源的，其結果下面展示。

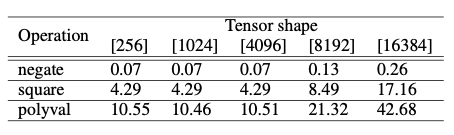
顯示了不同算術運算的平均效能。具體來說一元操作的持續時間（毫秒）。CKKS的context是由模多項式的級數8192和係數模數200位建立的。polyval benchmark是針對\(2X^2+X\)執行的。

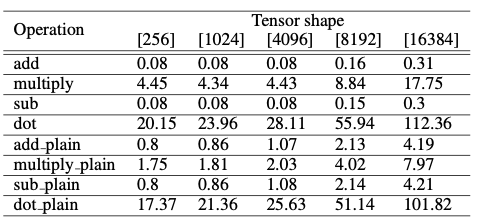
顯示了矩陣乘法的平均效能。具體來說，二元操作的持續時間（毫秒）。CKKS的context是由模多項式級數8192和係數模數200位建立的。對於「明文」操作，運算元是shape相同的明文張量。對於其餘部分，運算元是shape相同的密文張量。

不足和總結

加密部分依賴於【paper：CKKS17】，這是Leveled-FHE方案。這意味著，根據我們的引數選擇，我們可以對密文資料執行的乘法數量是有限的，這直接影響我們可以使用的機器學習模型或其深度。不同的機器學習模型也使用非線性激勵函數，在CKKS的情況下，需要使用近似多項式計算）。最近的一項工作【paper：New challenges for fully homomorphic encryption】一直試圖通過使用TFHE方案【paper：Tfhe: fast fully homo- morphic encryption over the torus】來解決與機器學習密切相關的這個問題，該方案允許評估更深層次的模型以及非線性啟用函數。

最後，我們的結果表明，利用CKKS方案進行張量計算是可行的。根據使用情況，使用者可以選擇高階張量操作（slicing、broadcasting）或使用更多計算通訊優化實現。TenSEAL可以適應這兩種情況，同時提供從傳統機器學習框架的平穩過渡。最後，我們試圖擴充套件tensor operations catalog，並進一步提高整體效能。