一起來分析Python佇列相關應用與習題

推薦學習：

0. 學習目標

我們已經學習了佇列的相關概念以及其實現，同時也瞭解了佇列在實際問題中的廣泛應用，本節的主要目的是通過佇列的相關習題來進一步加深對佇列的理解，同時能夠利用佇列降低一些複雜問題解決方案的時間複雜度。

1. 使用兩個棧實現一個佇列

[問題] 給定兩個棧，僅使用棧的基本操作實現一個佇列。

[思路] 解決此問題的關鍵在於棧的反轉特性，入棧的一系列元素在出棧時會以相反的順序返回。因此，使用兩個棧就可以實現元素以相同的順序返回(反轉的元素序列再次反轉後就會得到原始順序)。具體操作如下圖所示：

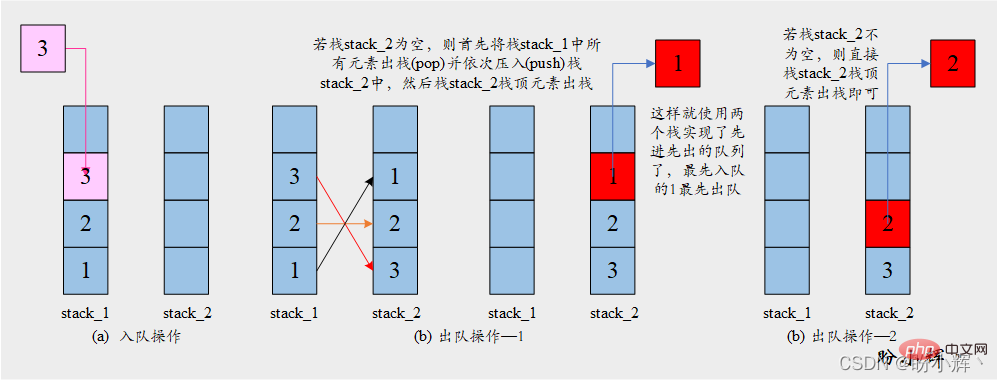
[演演算法]

 入隊 enqueue：
   將元素推入棧 stack_1
 出隊 dequeue：
   如果棧 stack_2 不為空：
     stack_2 棧頂元素出棧
   否則：
     將所有元素依次從 stack_1 彈出並壓入 stack_2
     stack_2 棧頂元素出棧

[程式碼]

class Queue:
    def __init__(self):
        self.stack_1 = Stack()
        self.stack_2 = Stack()
    def enqueue(self, data):
        self.stack_1.push(data)
    def dequeue(self):
        if self.stack_2.isempty():
            while not self.stack_1.isempty():
                self.stack_2.push(self.stack_1.pop())
        return self.stack_2.pop()

[時空複雜度] 入隊時間複雜度為$O(1)$，如果棧 stack_2 不為空，那麼出隊的時間複雜度為 $O(1)$，如果棧 stack_2 為空，則需要將元素從 stack_1 轉移到 stack_2，但由於 stack_2 中轉移的元素數量和出隊的元素數量是相等的，因此出隊的攤銷時間複雜度為 $O(1)$。

2. 使用兩個佇列實現一個棧

[問題] 給定兩個佇列，僅使用佇列的基本操作實現一個棧。

[思路] 由於佇列並不具備反轉順序的特性，入隊順序即為元素的出隊順序。因此想要獲取最後一個入隊的元素，需要首先將之前所有元素出隊。因此為了使用兩個佇列實現棧，我們需要將其中一個佇列 store_queue 用於儲存元素，另一個佇列 temp_queue 則用來儲存為了獲取最後一個元素而儲存臨時出隊的元素。push 操作將給定元素入隊到儲存佇列 store_queue 中；pop 操作首先把儲存佇列 store_queue 中除最後一個元素外的所有元素都轉移到臨時佇列 temp_queue 中，然後儲存佇列 store_queue 中的最後一個元素出隊並返回。具體操作如下圖所示：

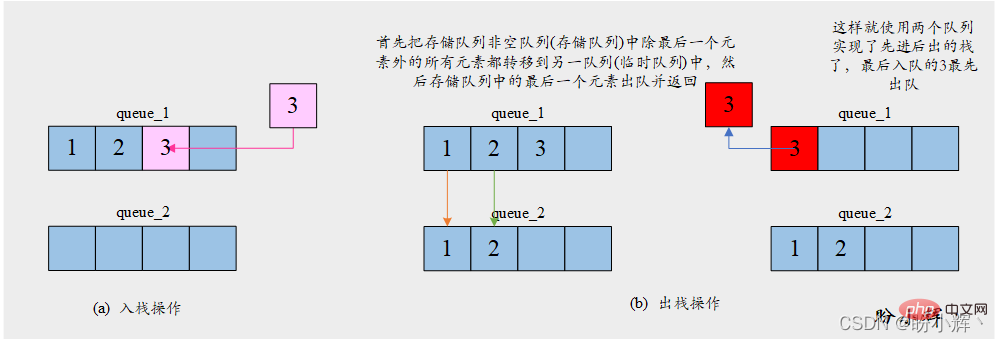
[演演算法]

 演演算法執行過程需要始終保持其中一個佇列為空，用作臨時佇列
 入棧 push：在非空佇列中插入元素 data。
   若佇列 queue_1 為空：
     將 data 插入 佇列 queue_2 中
   否則：
     將 data 插入 佇列 queue_1 中
 出棧 pop：將佇列中的前$n-1$ 個元素插入另一佇列，刪除並返回最後一個元素
   若佇列 queue_1 不為空：
     將佇列 queue_1 的前$n-1$ 個元素插入 queue_2，然後 queue_1 的最後一個元素出隊並返回
   若佇列 queue_2 不為空：
     將佇列 queue_2 的前$n-1$ 個元素插入 queue_1，然後 queue_2 的最後一個元素出隊並返回

[程式碼]

class Stack:
    def __init__(self):
        self.queue_1 = Queue()
        self.queue_2 = Queue()
    def isempty(self):
        return self.queue_1.isempty() and self.queue_2.isempty()
    def push(self, data):
        if self.queue_2.isempty():
            self.queue_1.enqueue(data)
        else:
            self.queue_2.enqueue(data)
    def pop(self):
        if self.isempty():
            raise IndexError("Stack is empty")
        elif self.queue_2.isempty():
            while not self.queue_1.isempty():
                p = self.queue_1.dequeue()
                if self.queue_1.isempty():
                    return p
                self.queue_2.enqueue(p)
        else:
            while not self.queue_2.isempty():
                p = self.queue_2.dequeue()
                if self.queue_2.isempty():
                    return p
                self.queue_1.enqueue(p)

[時空複雜度] push 操作的時間複雜度為$O(1)$，由於 pop 操作時，都需要將所有元素從一個佇列轉移到另一佇列，因此時間複雜度$O(n)$。

3. 棧中元素連續性判斷

[問題] 給定一棧 stack1，棧中元素均為整數，判斷棧中每對連續的數位是否為連續整數(如果棧有奇數個元素，則排除棧頂元素)。例如，輸入棧 [1, 2, 5, 6, -5, -4, 11, 10, 55]，輸入為 True，因為排除棧頂元素 55 後，(1, 2)、(5, 6)、(-5, -4)、(11, 10) 均為連續整數。

[思路] 由於棧中可能存在奇數個元素，因此為了正確判斷，首次需要將棧中元素反轉，棧頂元素變為棧底，然後依次出棧，進行判斷。

[演演算法]

 棧 stack 中所有元素依次出棧，並插入佇列 queue 中
 佇列 queue 中所有元素出隊，併入棧 stack
  while 棧 stack 不為空：
   棧頂元素 e1 出棧，並插入佇列 queue 中
   如果棧 stack 不為空：
     棧頂元素 e2 出棧，並插入佇列 queue 中
     如果 |e1-e2|!=1：
       返回 False，跳出迴圈
 佇列 queue 中所有元素出隊，併入棧 stack

[程式碼]

def check_stack_pair(stack):
    queue = Queue()
    flag = True
    # 反轉棧中元素
    while not stack.isempty():
        queue.enqueue(stack.pop())
    while not queue.isempty():
        stack.push(queue.dequeue())
    while not stack.isempty():
        e1 = stack.pop()
        queue.enqueue(e1)
        if not stack.isempty():
            e2 = stack.pop()
            queue.enqueue(e2)
            if abs(e1-e2) != 1:
                flag = False
                break
    while not queue.isempty():
        stack.push(queue.dequeue())
    return flag

[時空複雜度] 時間複雜度為$O(n)$，空間複雜度為$O(n)$。

4. 重新排列佇列中元素順序

[問題] 給定一個整數佇列 queue，將佇列的前半部分與佇列的後半部分交錯來重新排列元素。例如輸入佇列為 [1, 2, 3, 4, 5, 6, 7, 8, 9]，則輸出應為 [1, 6, 2, 7, 3, 8, 4, 9, 5]。

[思路] 通過獲取佇列的前半部分，然後利用棧的反轉特性，可以實現重排操作，如下圖所示：

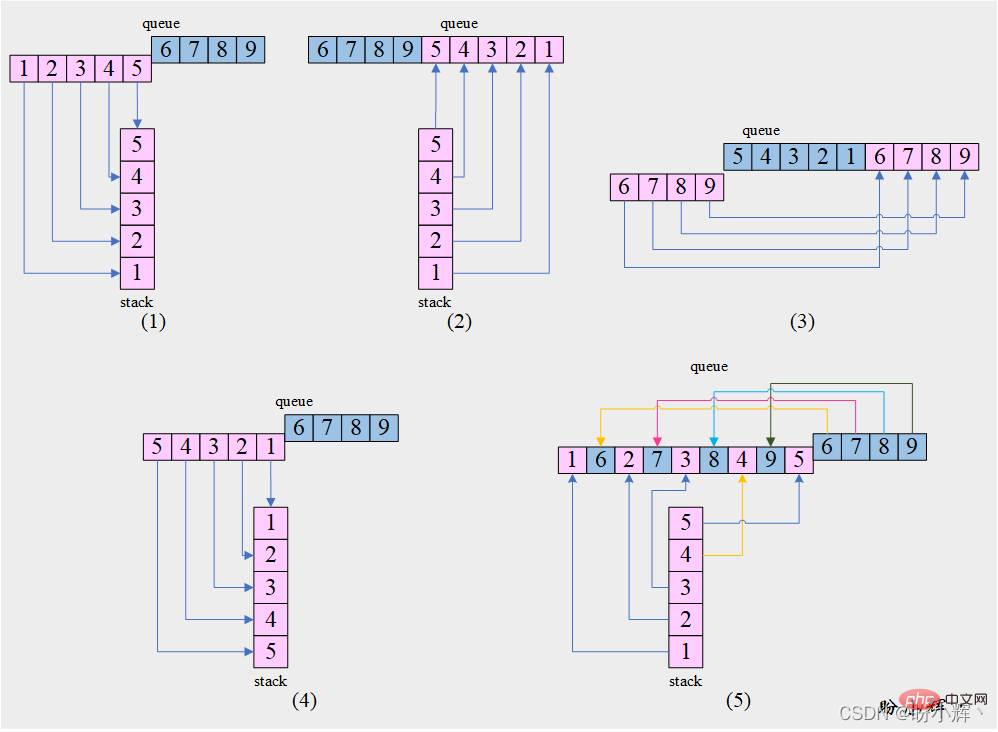
[演演算法]

 如果佇列 queue 中的元素數為偶數：
   half=queue.size//2
 否則：
   half=queue.size//2+1
 1. 將佇列 queue 的前半部分元素依次出隊併入棧 stack
 2. 棧 stack 中元素出棧併入隊 queue
 3. 將佇列 queue 中在步驟 1中未出隊的另一部分元素依次出隊並插入隊尾
 4. 將佇列 queue 的前半部分元素依次出隊併入棧 stack
 5. 將棧 stack 和佇列 queue 中的元素交替彈出併入隊
 6. 如果棧 stack 非空：
   棧 stack 中元素出棧併入隊

[程式碼]

def queue_order(queue):
    stack = Stack()
    size = queue.size    if size % 2 == 0:
        half = queue.size//2
    else:
        half = queue.size//2 + 1
    res = queue.size - half    for i in range(half):
        stack.push(queue.dequeue())
    while not stack.isempty():
        queue.enqueue(stack.pop())
    for i in range(res):
        queue.enqueue(queue.dequeue())
    for i in range(half):
        stack.push(queue.dequeue())
    for i in range(res):
        queue.enqueue(stack.pop())
        queue.enqueue(queue.dequeue())
    if not stack.isempty():
        queue.enqueue(stack.pop())

[時空複雜度] 時間複雜度為$O(n)$，空間複雜度為$O(n)$。

5. 反轉佇列中前 m 個元素的順序

[問題] 給定一個整數 m 和一個整數佇列 queue，反轉佇列中前 k 個元素的順序，而其他元素保持不變。如 m=5，佇列為 [1, 2, 3, 4, 5, 6, 7, 8, 9]，演演算法輸出為 [5, 4, 3, 2, 1, 6, 7, 8, 9]。

[思路] 結合 [問題4] 我們可以發現，此題就是 [問題4] 的前 3 步，如下圖所示：

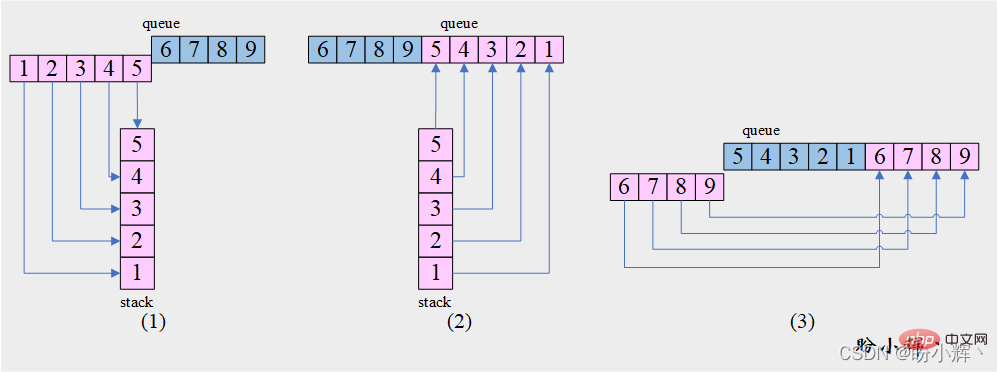
[演演算法]

 1. 將佇列 queue 的前 m 個元素依次出隊併入棧 stack
 2. 棧 stack 中元素出棧併入隊 queue
 3. 將佇列 queue 中在步驟 1中未出隊的另一部分元素依次出隊並插入隊尾

[程式碼]

def reverse_m_element(queue, m):
    stack = Stack()
    size = queue.size    if queue.isempty() or m>size:
        return
    for i in range(m):
        stack.push(queue.dequeue())
    while not stack.isempty():
        queue.enqueue(stack.pop())
    for i in range(size-m):
        queue.enqueue(queue.dequeue())

[時空複雜度] 時間複雜度為$O(n)$，空間複雜度為 $O(n)$。

推薦學習：

以上就是一起來分析Python佇列相關應用與習題的詳細內容，更多請關注TW511.COM其它相關文章！