分享一道邏輯面試題，看看你能答對嗎！

01 故事起源

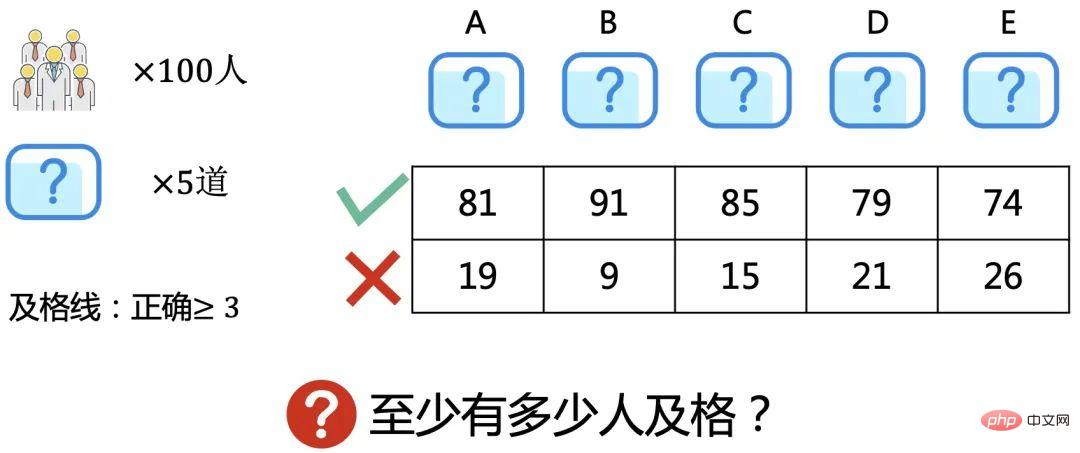
100個人回答五道題，有81人答對第一題，91人答對第二題，85人答對第三題，79人答對第四題，74人答對第五題。

答對三道題或三道題以上的人算及格，那麼在這100人中至少有多少人及格呢？

02 思考小規模，AB兩題

先考慮如果只有AB兩道題，100個人，第一反應是用集合的方式。

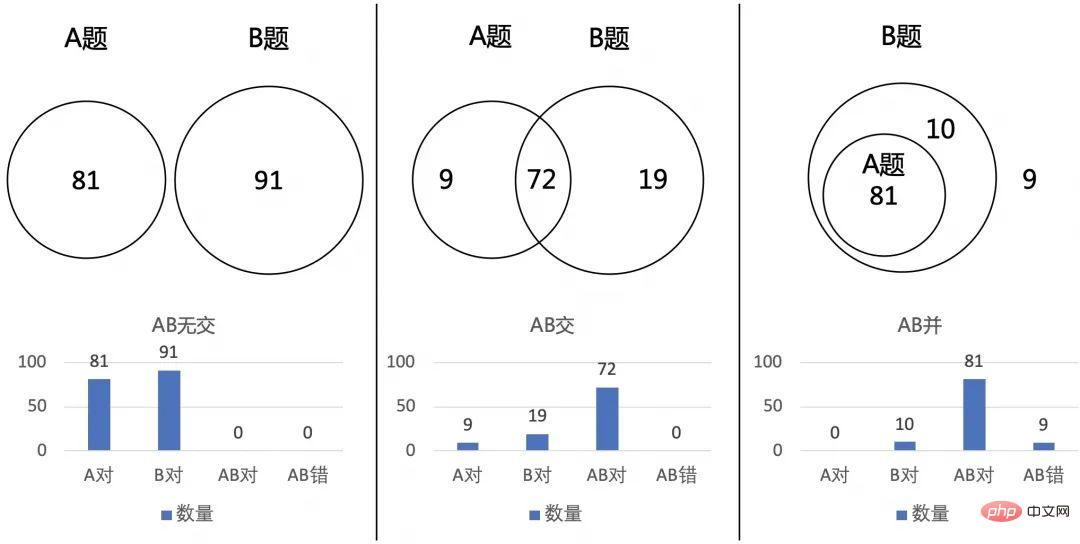
總共也就上面3種情況，其中第一種人數大於100非法，所以只存在後面2種情況。
可以得到如下結論：

• 同時做對AB兩題的最少有72人，最多有81人；

• 同時做錯AB兩題的最多有9人，最少有0人。

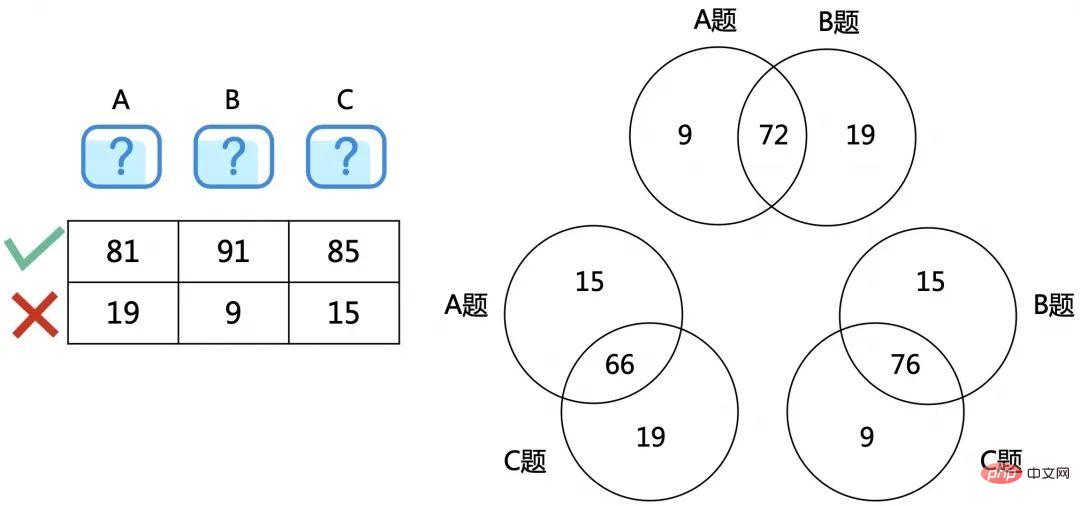
看來已經找到了規律，那就按這個思路進一步擴巨量資料規模，考慮ABC三題。

03 擴大規模，ABC三題

先考慮每兩題之間的關係。

再合成三題的關係。等等，好像有點複雜，這不是線性的複雜度，不好意思，小K的智商有點不夠用，自閉了。

那小K是不是要準備放棄了呢，NO，never say give up。有時候不要撞倒南牆不回頭，基於小K多年的經驗，如果找到的規律不明顯或者很複雜，一般都說明你走錯了，所以這時要考慮切換思維方式。

04 切換思維

上面都是正向思維，但不好處理，可以逆向思維。

只要錯3道就不及格，一共有19+9+15+21+26=90道錯題，那麼90/3=30，則最多有30人不及格，所以最少有70人及格，perfect，收工。

Wait，總感覺有點怪怪的，倒不是因為太簡單，而是對於資訊量的直覺告訴我，這種解法忽略了很多的資訊量。

只用了總數，而沒有用到5道題的錯題數量分佈。那就直接告訴你總共錯了90道就行了，為啥還要單獨告訴具體的數量，這難道真的只是誤導資訊嗎？

05 極限法思維

根據上面的解法，既然不關心具體分佈，那就用極限思維，構造特殊資料。比如所有錯題集中在A題。

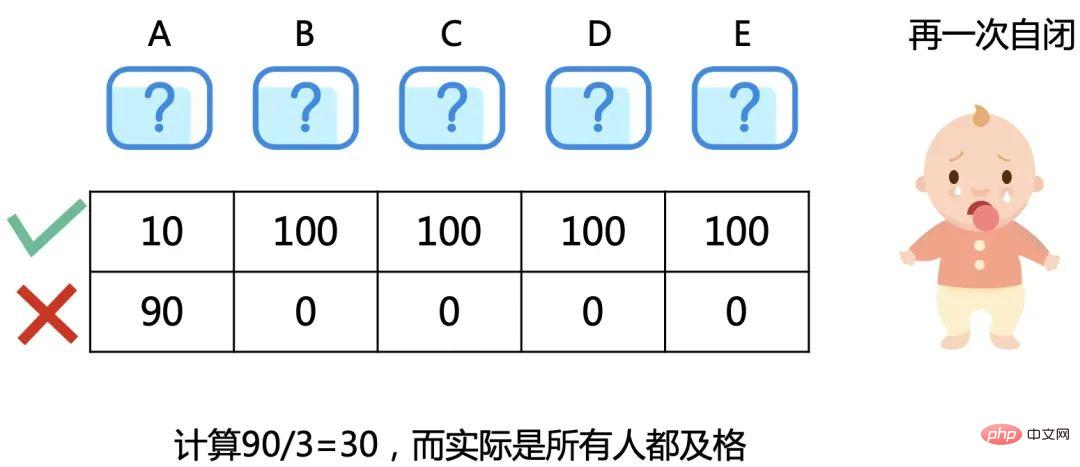
總共還是錯90道，但所有人都做對4題，應該是100人及格，再一次自閉。

這時，我想應該有槓精要跳出來了。

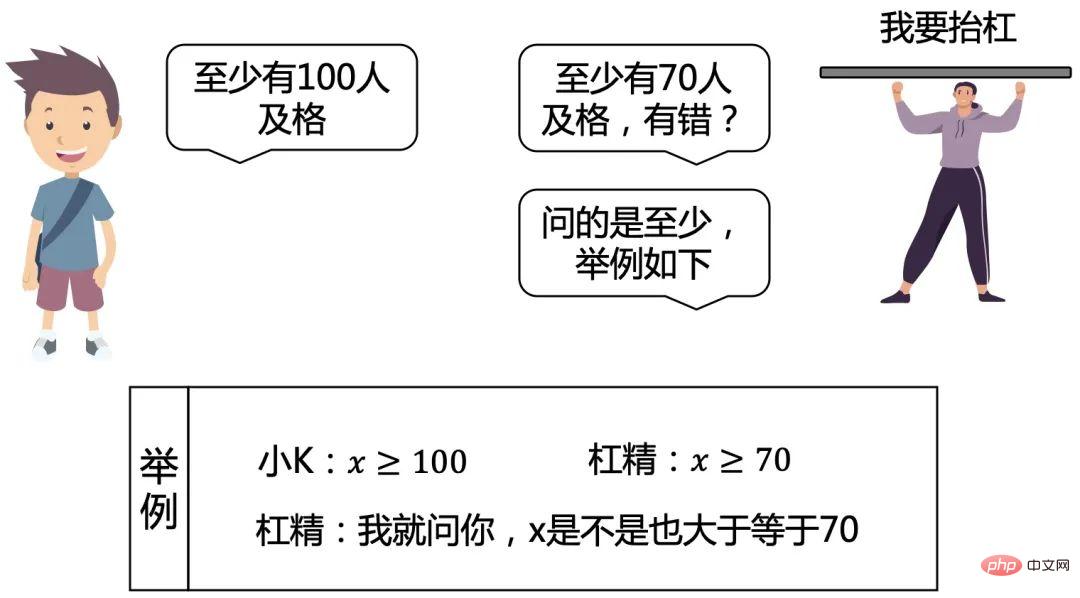
小K：你說得很有道理，我竟無言以對。
先不跟你扯，咱們進一步思考，這個反例說明了一點：錯題不能隨意均攤，那就從這點下手。

06 錯題均攤

先看錯誤的分佈。

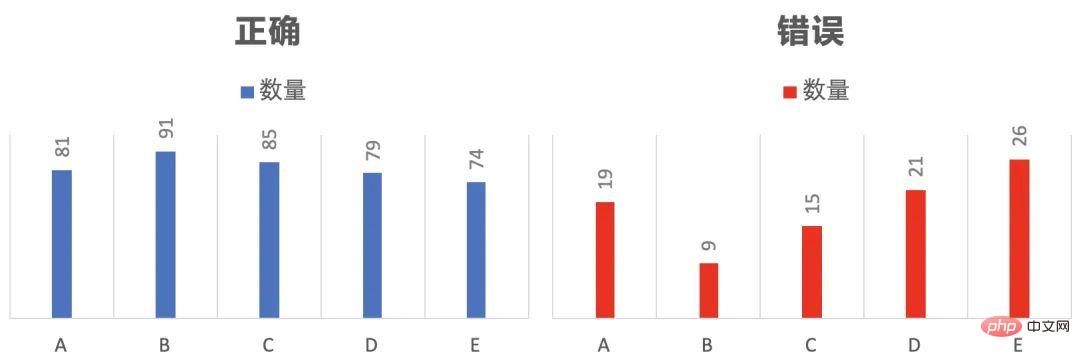
如何將這些錯題分配給最多的人。

為了分析方便，先寫一個簡單的例子，如錯題分佈為7、8、9、10、11。

第一種分配：

• 將A,B,C分配給7人

• 將C,D,E分配給2人

• 將B,D,E分配給1人

總共可分配7+2+1=10人。

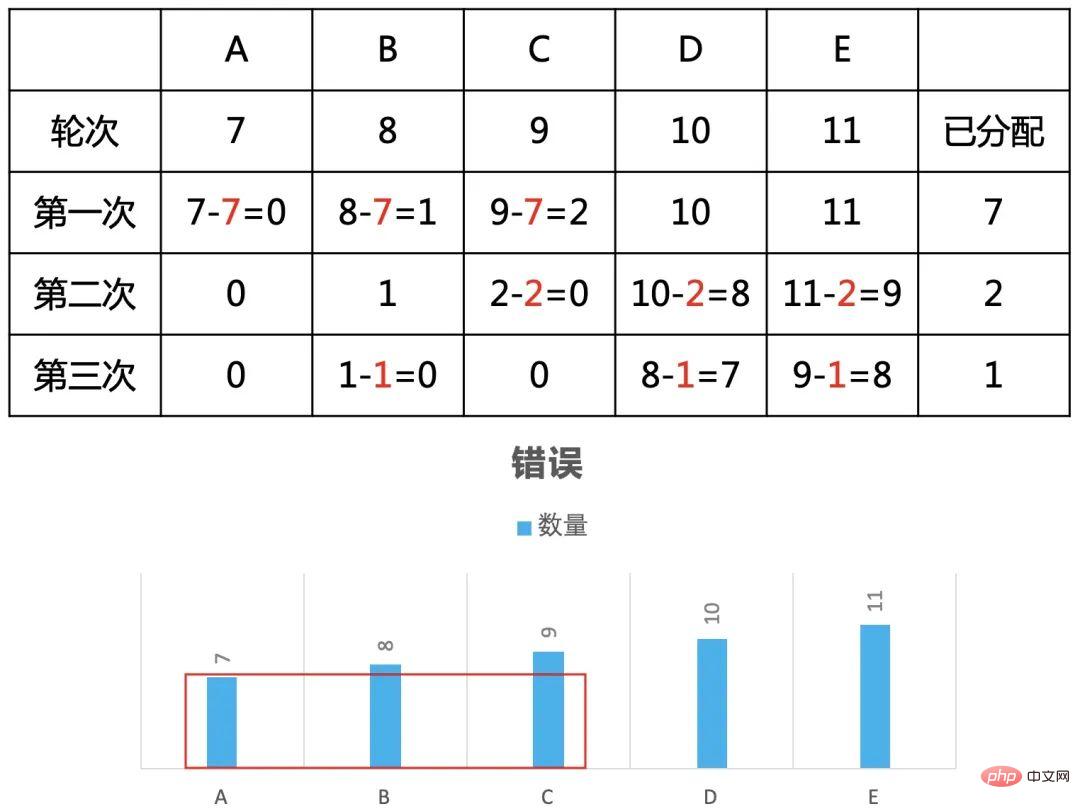
第二種，優先分配B,C,D，總共11人。

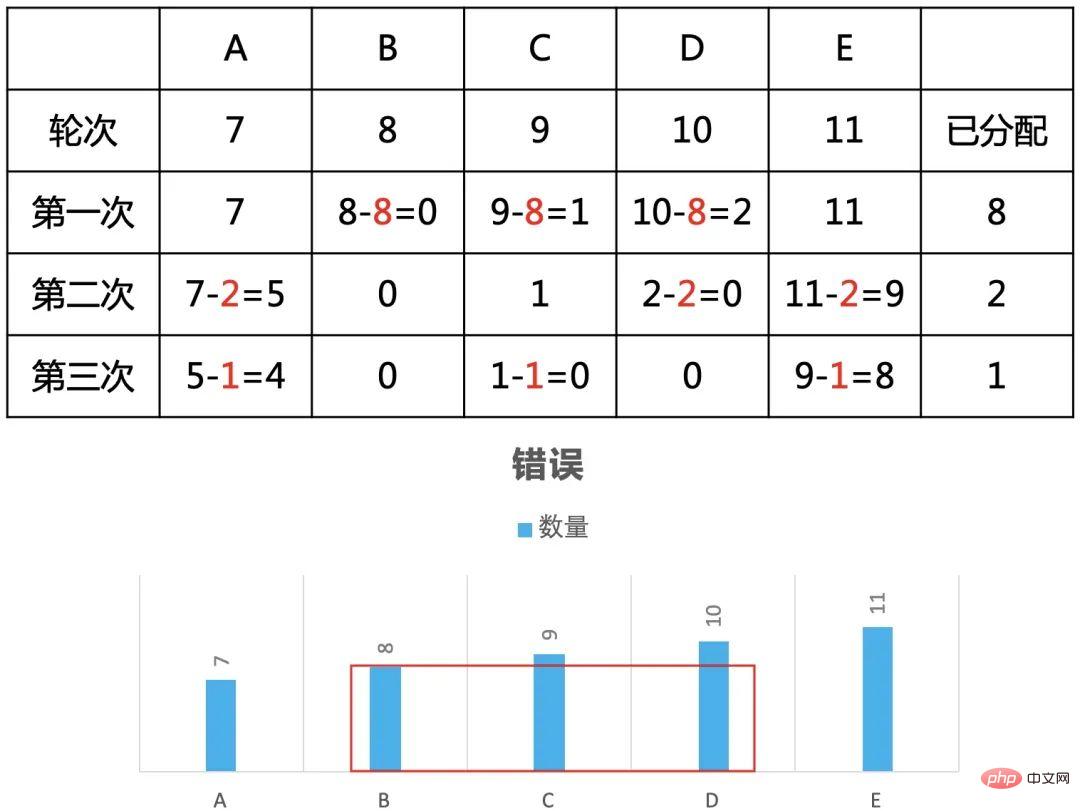
第三種，優先分配C,D,E，總共12人。

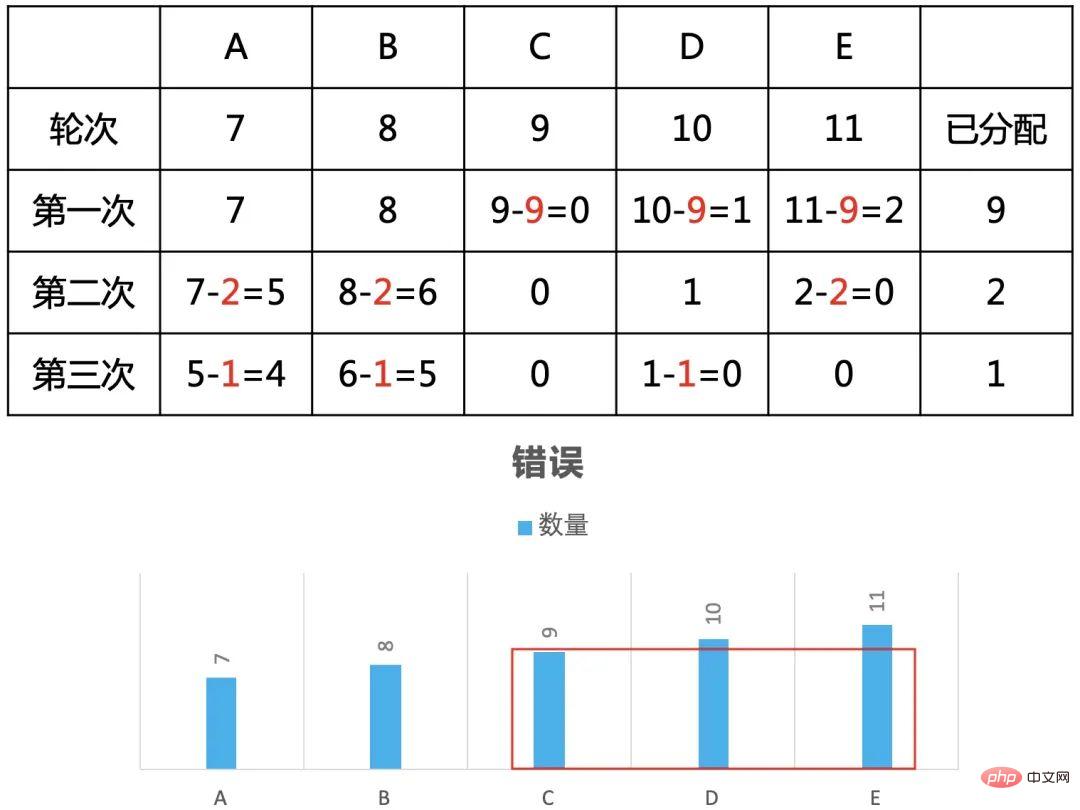
到這裡我們已經發現了規律，優先分配最大的3道會得到更多的人數。而在分配過程中最大的3道順序會動態變化，這就啟發了貪心的思想。

• 將錯題從大到小排序；

• 每次將最大的前3個分配給一人，然後重新排序。

重複上面步驟，直到最後找不出3個不為0的數，也就是變為X,0,0,0,0或者X,Y,0,0,0。

07 抽象

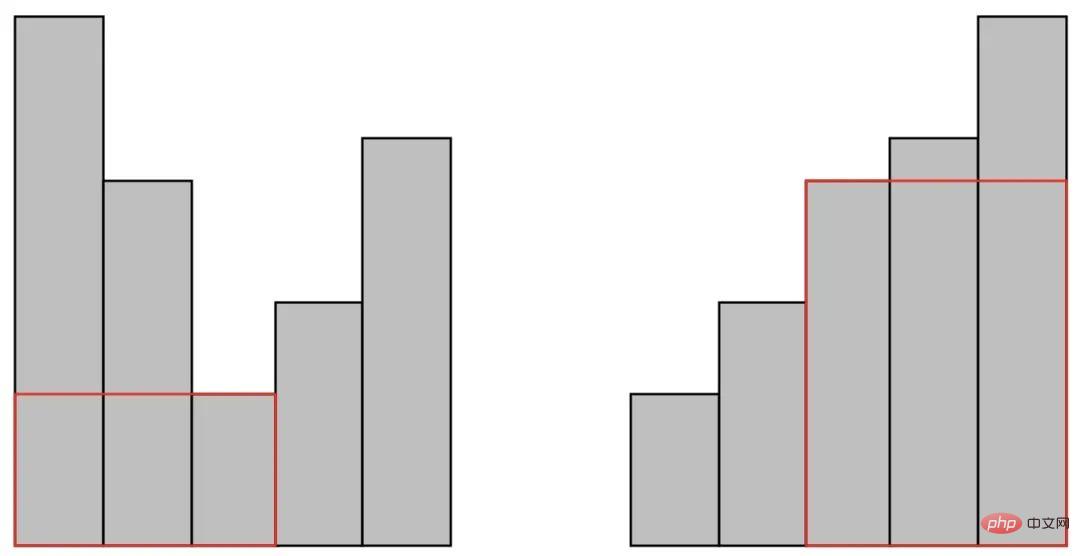
轉換問題：有5個矩形，順序可隨意。要切出寬度為3的N個矩形，要求總體疊加要儘量的高，最高有多少?
你品，你細品，這是不是同一個問題呀。所以要從最高的前3個開始一點一點地削它，哈哈。

08 真相浮出水面

回到原題，那到底至少有多少人呢？通過程式碼測試結果。

8.1 程式碼實現

int main() {
    int a[5], ans = 0;
    for (int i = 0; i < 5; ++i) {
        cin >> a[i];
    }
    sort(a, a + 5, compare);
    while (a[2] > 0) {
        a[0]--;
        a[1]--;
        a[2]--;
        sort(a, a + 5, compare);
        ans++;
        for (int i = 0; i < 5; ++i) {
            cout << a[i] << " ";
        }
        cout << endl;
    }
    cout << "ans=" << ans << endl;

    return 0;
}

8.2 資料測試

25 20 18 15 9 
24 19 17 15 9 
23 18 16 15 9 
22 17 15 15 9 
21 16 15 14 9 
20 15 14 14 9 
19 14 14 13 9 
18 13 13 13 9 
17 13 12 12 9 
16 12 12 11 9 
15 11 11 11 9 
14 11 10 10 9 
13 10 10 9 9 
12 9 9 9 9 
11 9 9 8 8 
10 8 8 8 8 
9 8 8 7 7 
8 7 7 7 7 
7 7 7 6 6 
6 6 6 6 6 
6 6 5 5 5 
5 5 5 5 4 
5 4 4 4 4 
4 4 4 3 3 
3 3 3 3 3 
3 3 2 2 2 
2 2 2 2 1 
2 1 1 1 1 
1 1 1 0 0 
0 0 0 0 0 
ans=30

所以至多30人不及格，則至少70人及格，答案雖然一樣，但思維方式卻不一樣。

09 總結

看似簡單的問題，也要多深入思考，說不定你會發現不一樣的結論。而且也別輕易相信別人的分析，這個問題網上90%都是錯的，大家也可以看一下我的分析是否嚴謹，如果有問題也請留言反饋，謝謝啦。

相關推薦：《C語言視訊教學》、《》

以上就是分享一道邏輯面試題，看看你能答對嗎！的詳細內容，更多請關注TW511.COM其它相關文章！