資料結構—八大排序
本文所有排序以升序為例子
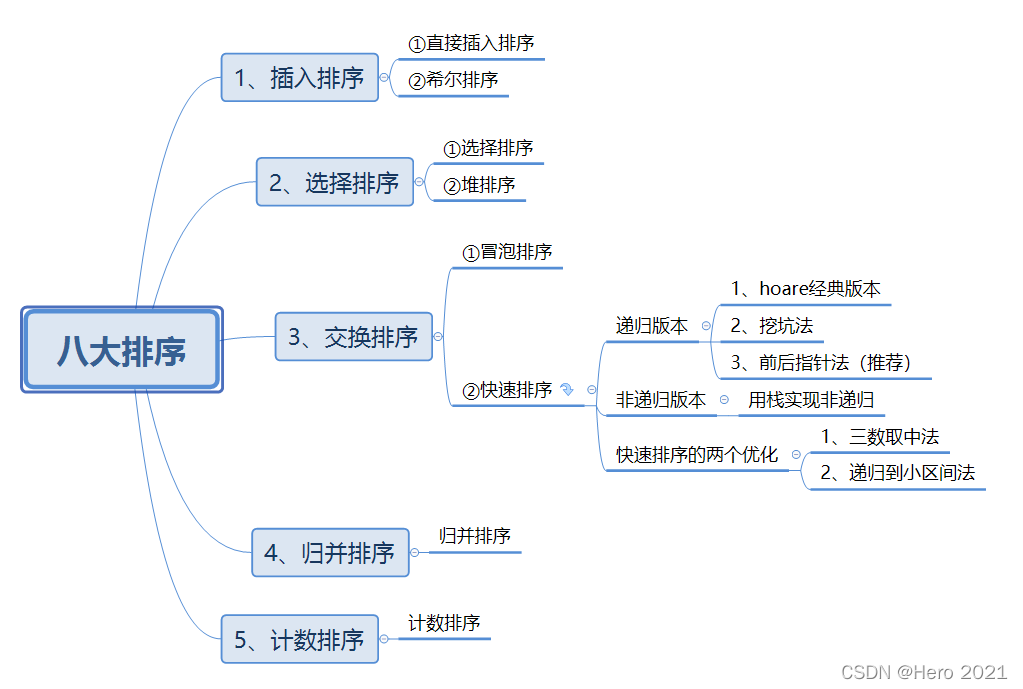
目錄
一、直接插入排序
基本思想:我們平時玩撲克牌時,摸牌階段的排序就用到了插入排序的思想
1、當插入第n個元素時,前面的n-1個數已經有序
2、用這第n個數與前面的n-1個數比較,找到要插入的位置,將其插入(原來位置上的數不會被覆蓋,因為提前儲存了)
3、原來位置上的資料,依次後移
具體實現:
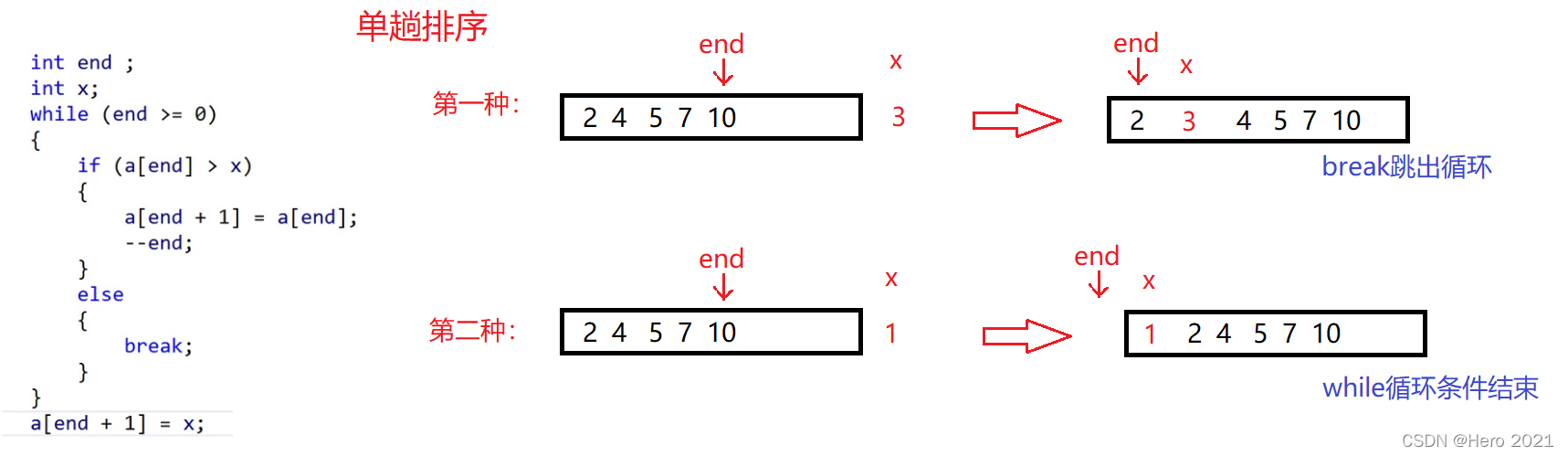
①單趟的實現(將x插入到 [0,end] 的有序區間)
即一般情況下的插入,我們隨機列舉了一些數位,待插入的數位分為兩種情況
(1)待插入的數位是在前面有序數位的中間數,直接比較將x賦值給end+1位置
(2)x是最小的一個數,end就會到達-1的位置,最後直接將x賦值給end+1位置
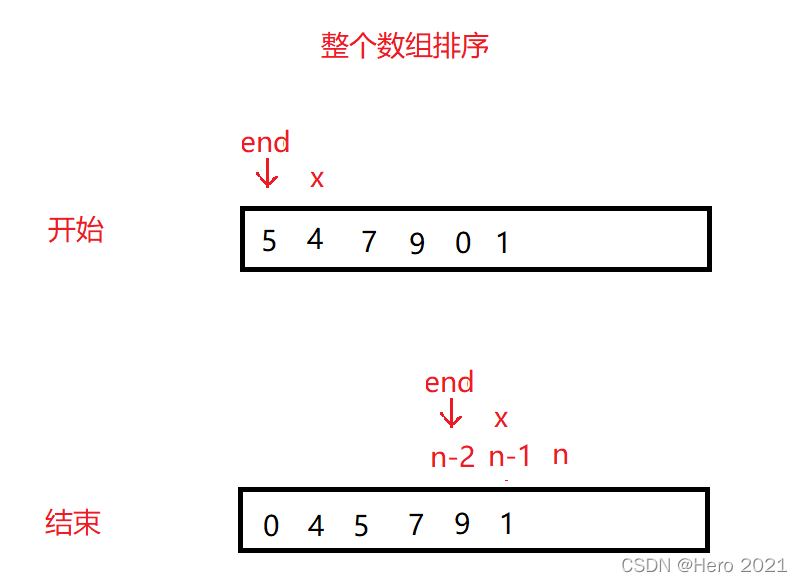
②整個陣列排序的實現
我們一開始並不知道陣列是不是有序的,所以我們控制下標,end從0開始,將end+1位置的值始終儲存到x中,迴圈進行單趟排序即可,最後結束時end=n-2,n-1位置的數位儲存到x中
總體程式碼:
void InsertSort(int* a, int n)
{
assert(a);
for (int i = 0; i < n - 1; ++i)
{
int end = i;
int x=a[end+1];//將end後面的值儲存到x裡面了
//將x插入到[0,end]的有序區間
while (end >= 0)
{
if (a[end] > x)
{
a[end + 1] = a[end]; //往後挪動一位
--end;
}
else
{
break;
}
}
a[end + 1] = x; //x放的位置都是end的後一個位置
}
}直接插入排序總結:
①元素越接近有序,直接插入排序的效率越高
②時間複雜度:O(N^2)
最壞的情況下,每次插入一個數位,前面的數位都要挪動一下,一共需要挪動1+2+3+……+n=n(n+1)/2
③空間複雜度:O(1)
沒有藉助額外的空間,只用到常數個變數
二、希爾排序
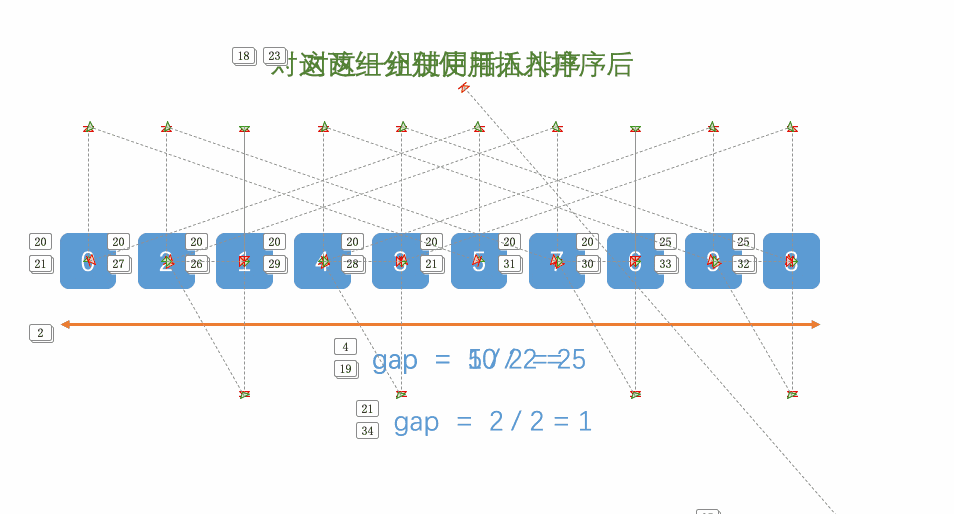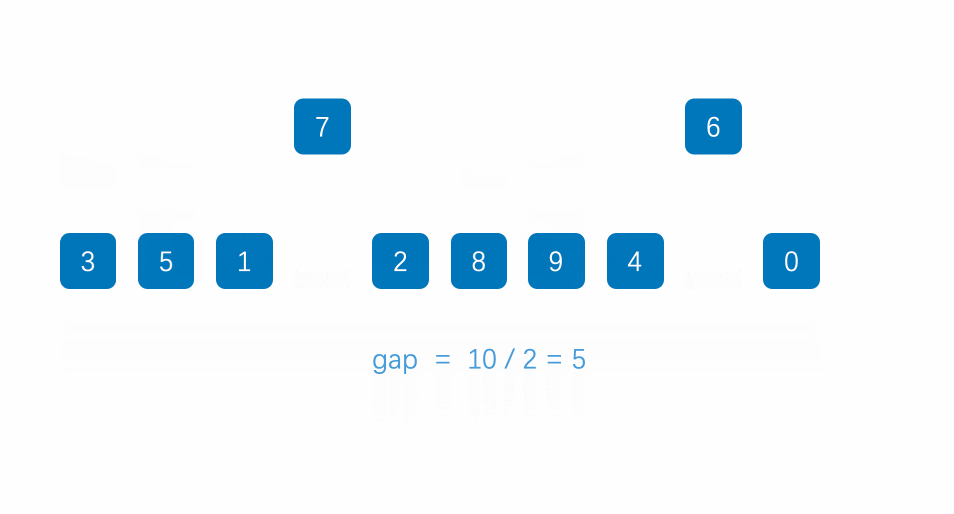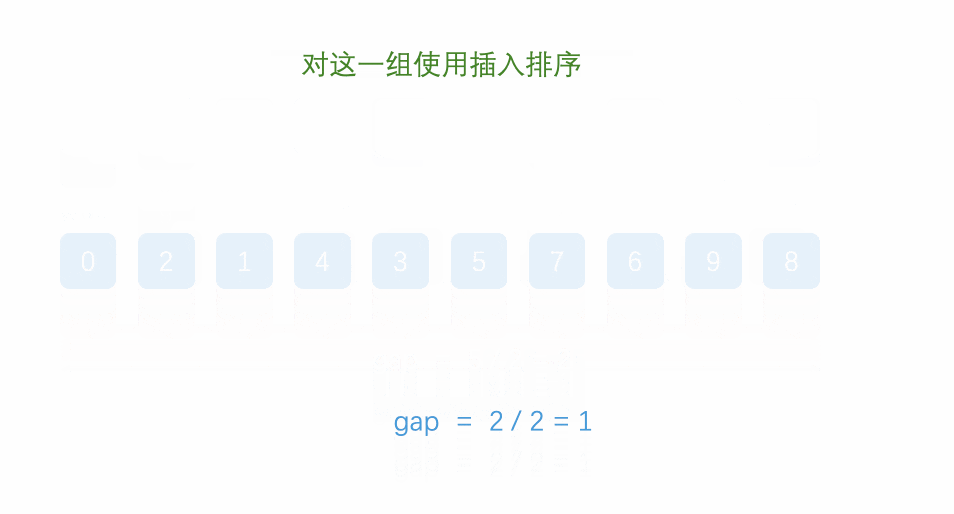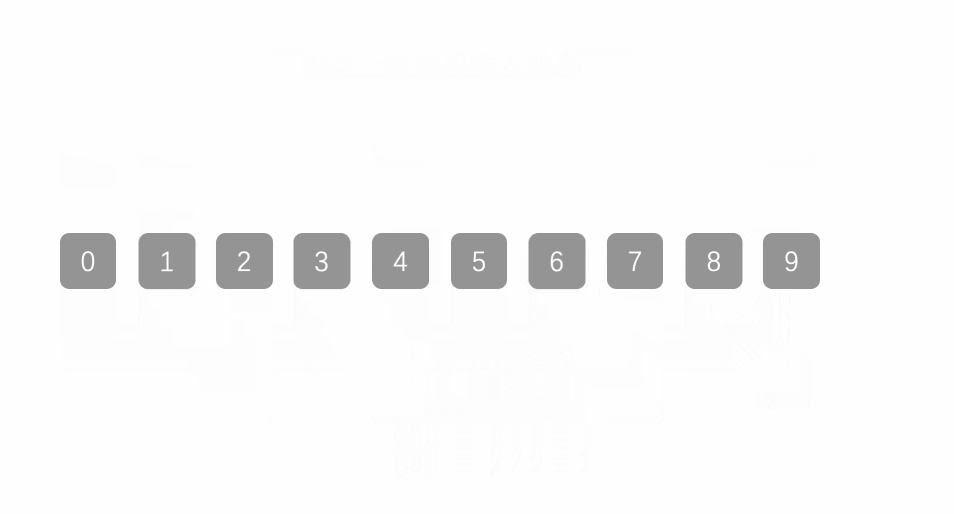
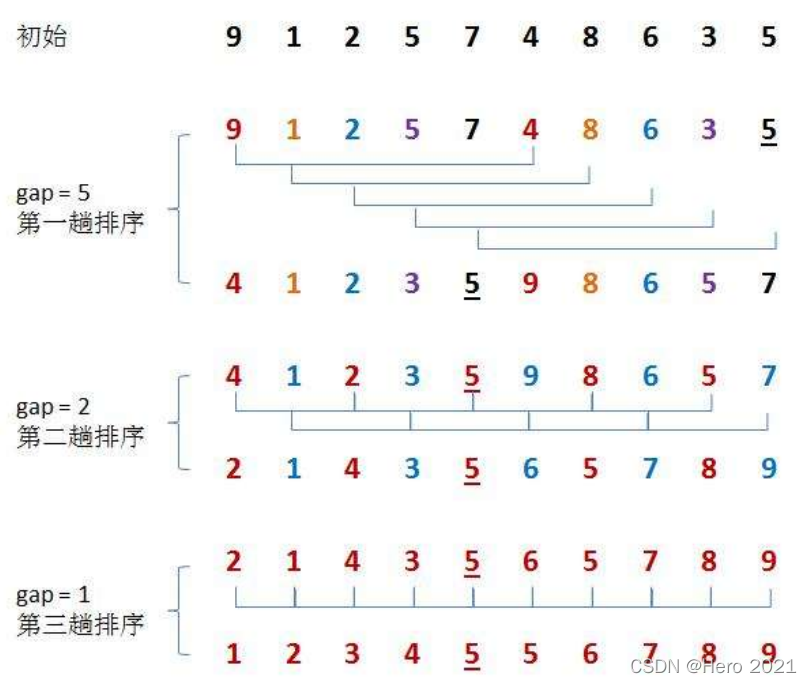
基本思想:
1、先選定個小於n的數位作為gap,所有距離為gap的數分為一組進行預排序(直接插入排序)
2、再選一個小於gap的數,重複①的操作
3、當gap=1時,相當於整個陣列就是一組,再進行一次插入排序即可整體有序
例如:
具體實現:
①單組排序
和前面的直接插入相同,就是把原來的間隔為1,現在變為gap了,每組分別進行預排序
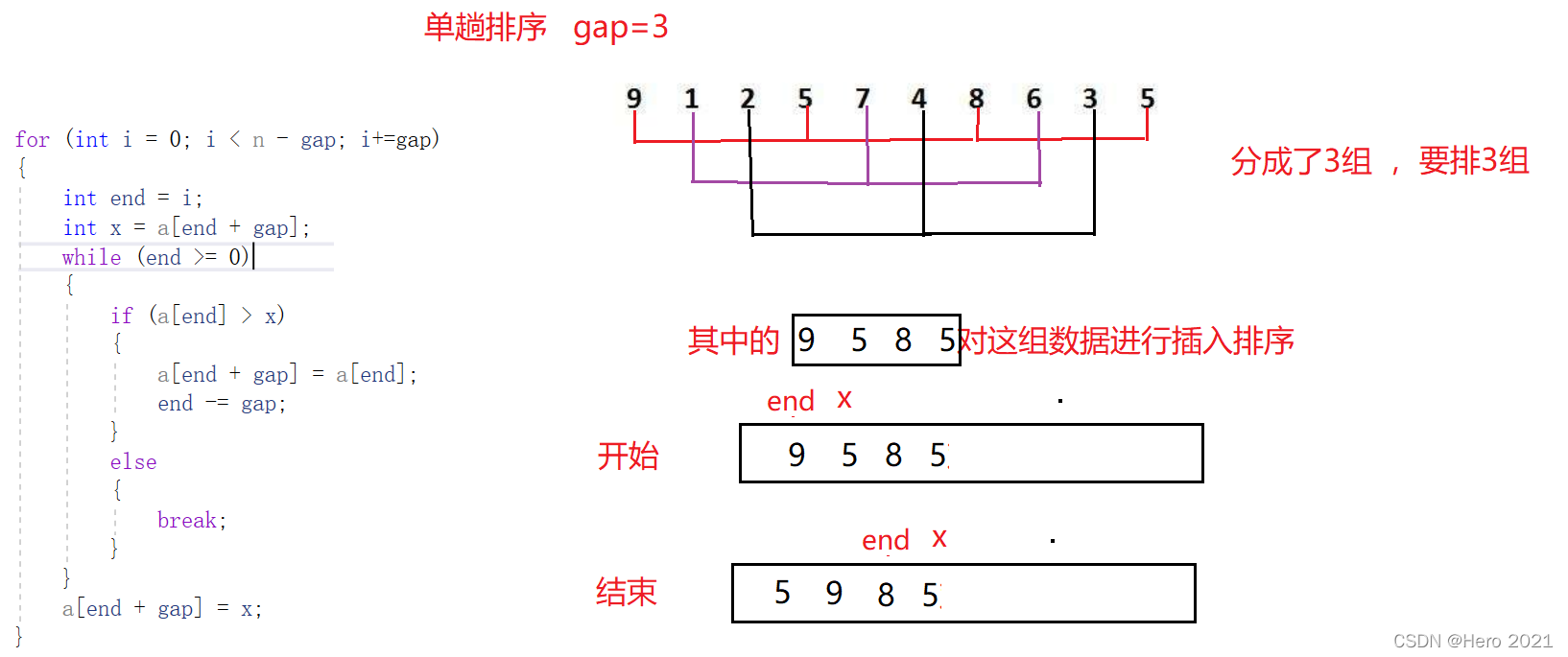
②多組進行排序
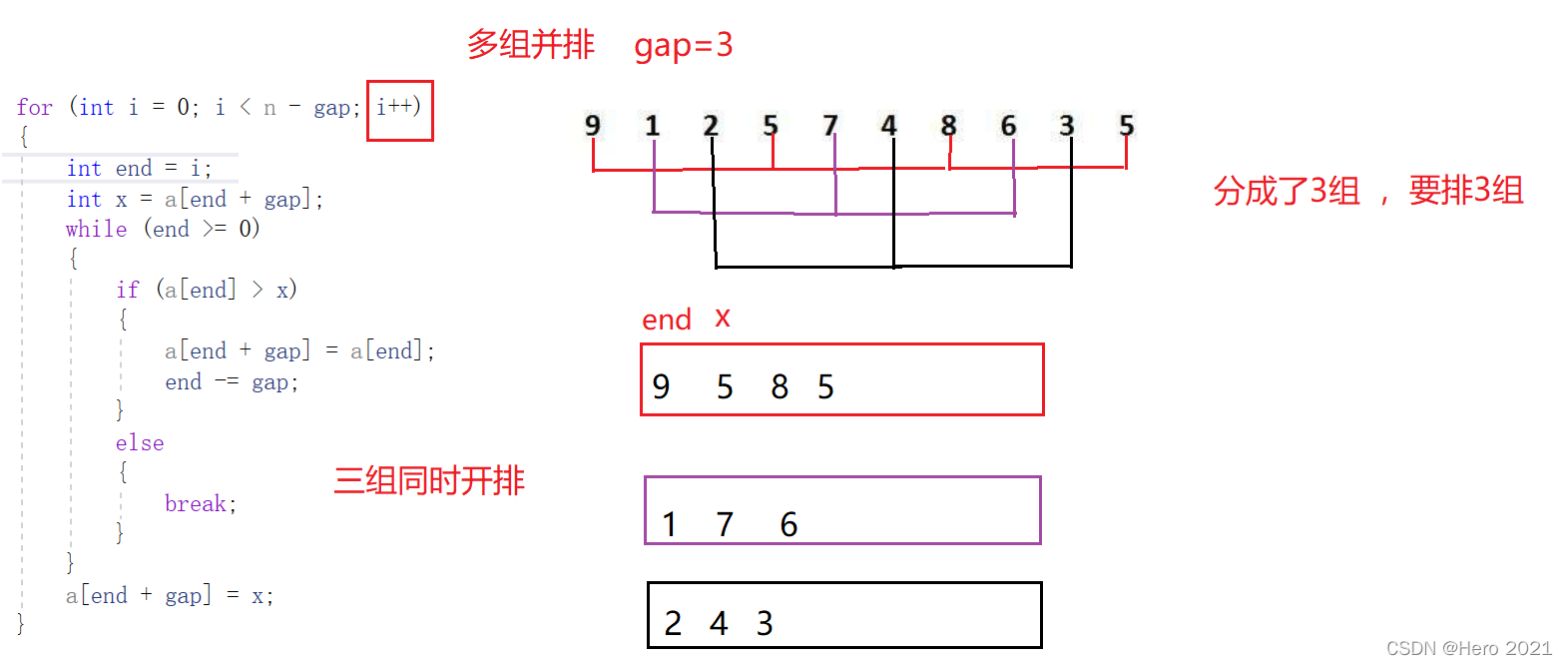
③整個陣列進行排序(控制gap)
多次預排序(gap>1)+ 一次插入排序(gap==1)
(1)gap越大,預排越快,越不接近於有序
(2)gap越小,預排越慢,越接近有序
結果就是:
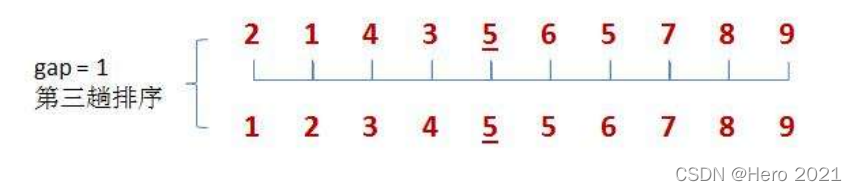
總體程式碼:
void ShellSort(int* a, int n)
{
int gap = n;
while (gap > 1)
{
gap /= 2;
for (int i = 0; i < n - gap; i++)
{
int end = i;
int x = a[end + gap];
while (end >= 0)
{
if (a[end] > x)
{
a[end + gap] = a[end];
end -= gap;
}
else
{
break;
}
}
a[end + gap] = x;
}
}
}希爾排序總結:
①希爾排序是對直接插入排序的優化
②時間複雜度:O(N^1.3)
③空間複雜度:O(1)
三、選擇排序 
基本思想:
每次從陣列中選出最大的或者最小的,存放在陣列的最右邊或者最左邊,直到全部有序
具體實現:
我們這裡進行了優化,一次排序中,直接同時選出最大的數(a[maxi])和最小的數(a[mini])放在最右邊和最左邊,這樣排序效率是原來的2倍
①單趟排序
找到最小的數位(a[mini])和最大的數位(a[maxi]),將他們放在最左邊和最右邊
ps:其中的begin,end儲存記錄左右的下標,mini,maxi記錄儲存最小值和最大值得下標
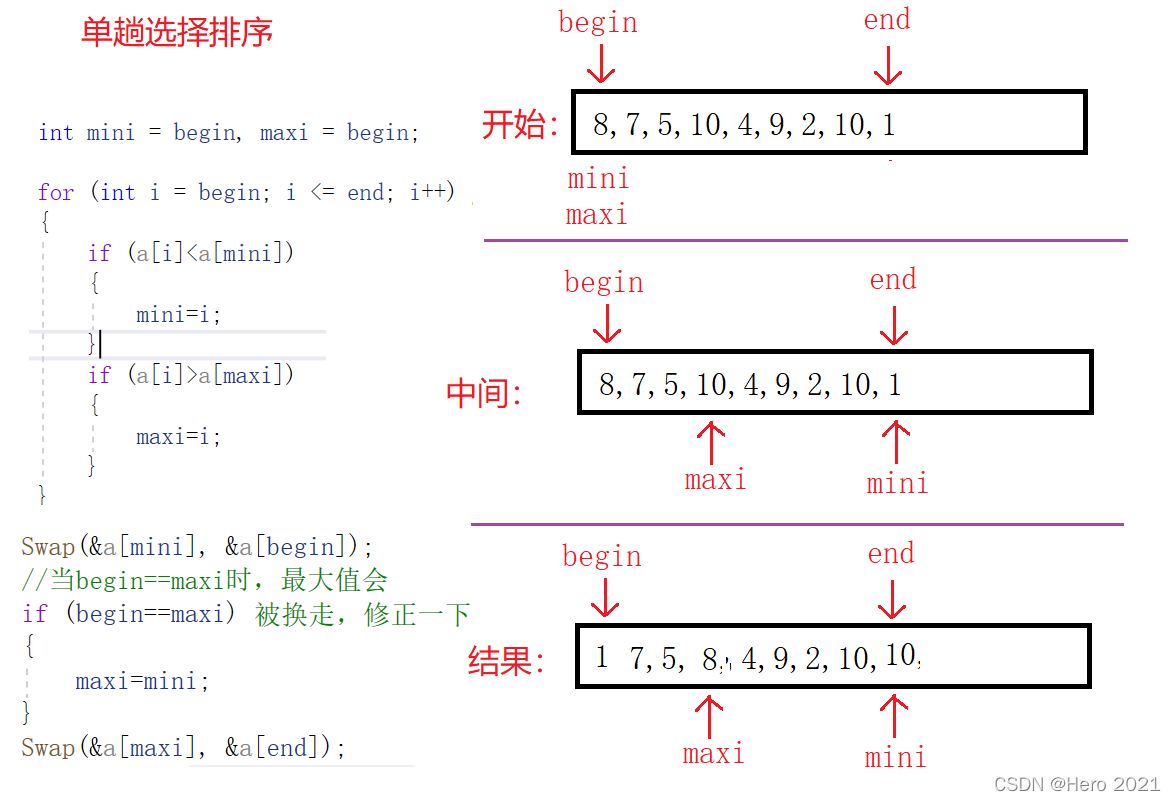
②整個陣列排序
begin++和end--這樣下次就可以排剩下的n-2個數位,再次進行單趟,如此可構成迴圈,直到begin小於end
整體程式碼:
void SelectSort(int* a, int n)
{
int begin = 0,end = n - 1;
while (begin<end)
{
int mini = begin, maxi = begin;
for (int i = begin; i <= end; i++)
{
if (a[i] < a[mini])
{
mini = i;
}
if (a[i] > a[maxi])
{
maxi = i;
}
}
Swap(&a[mini], &a[begin]);
//當begin==maxi時,最大值會被換走,修正一下
if (begin==maxi)
{
maxi=mini;
}
Swap(&a[maxi], &a[end]);
begin++;
end--;
}
}直接選擇排序總結:
①直接選擇排序很好理解,但實際效率不高,很少使用
②時間複雜度:O(N^2)
③空間複雜度:O(1)
四、堆排序
基本思想:
1、將待排序的序列構造成一個大堆,根據大堆的性質,當前堆的根節點(堆頂)就是序列中最大的元素;
2、將堆頂元素和最後一個元素交換,然後將剩下的節點重新構造成一個大堆;
3、重複步驟2,如此反覆,從第一次構建大堆開始,每一次構建,我們都能獲得一個序列的最大值,然後把它放到大堆的尾部。最後,就得到一個有序的序列了。
小結論:
排升序,建大堆
排降序,建小堆
具體實現:、
①向下調整演演算法
我們將給定的陣列序列,建成一個大堆,建堆從根節點開始就需要多次的向下調整演演算法
堆的向下調整演演算法(使用前提):
(1)若想將其調整為小堆,那麼根結點的左右子樹必須都為小堆。
(2)若想將其調整為大堆,那麼根結點的左右子樹必須都為大堆。
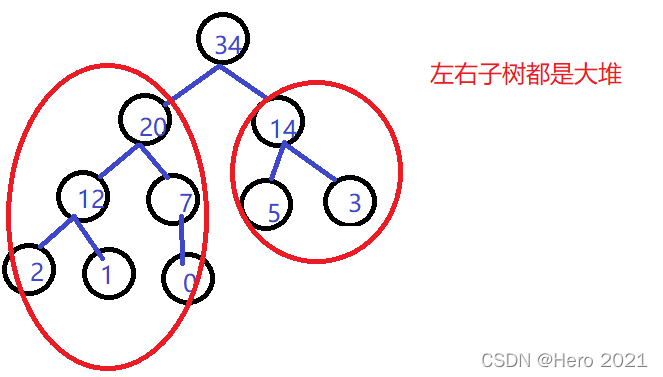
向下調整演演算法的基本思想:
1、從根節點開始,選出左右孩子值較大的一個
2、如果選出的孩子的值大於父親的值,那麼就交換兩者的值
3、將大的孩子看做新的父親,繼續向下調整,直到調整到葉子節點為止
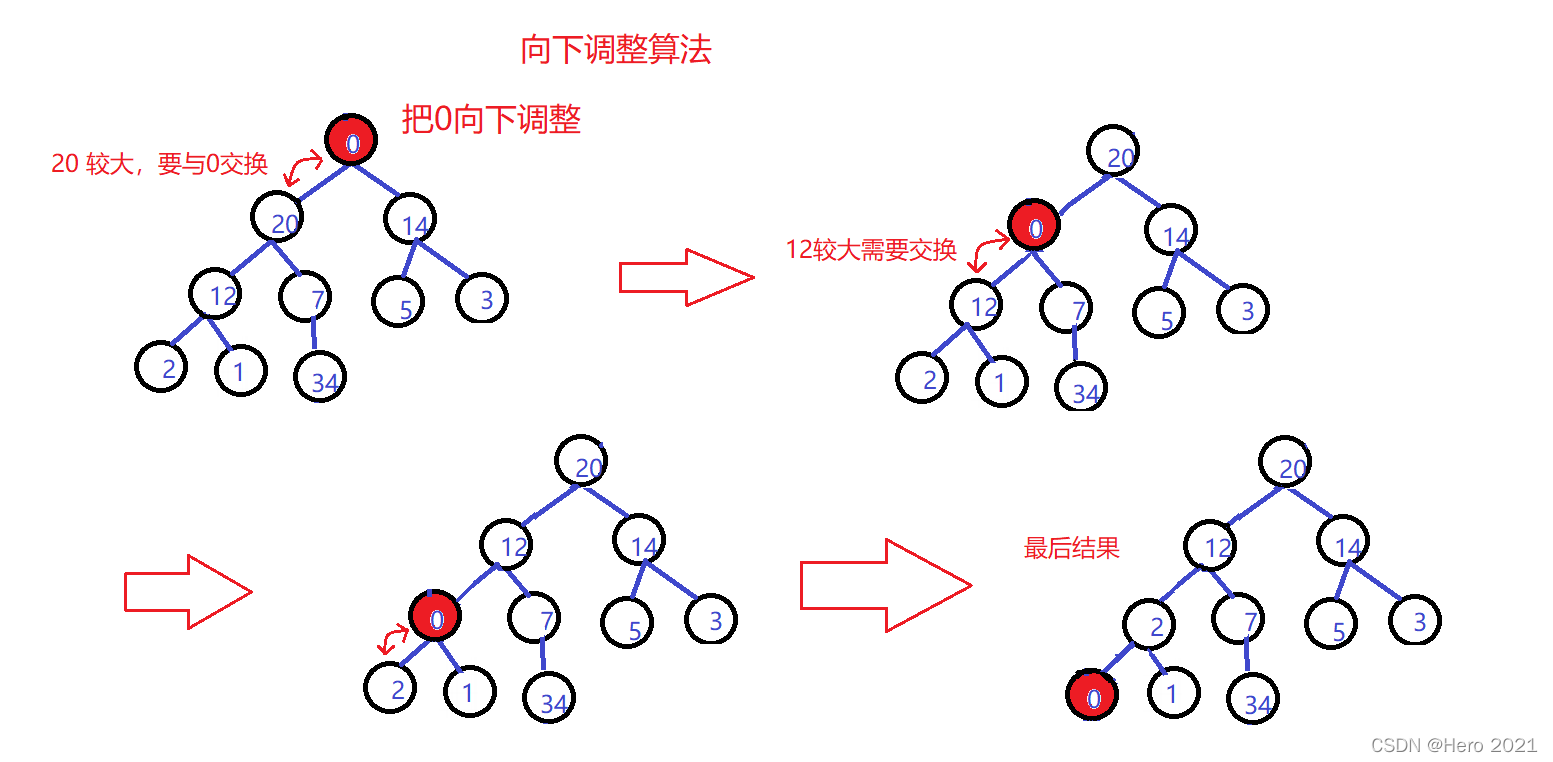
//向下調整演演算法
//以建大堆為例
void AdJustDown(int* a, int n, int parent)
{
int child = parent * 2 + 1;
//預設左孩子較大
while (child < n)
{
if (child + 1 < n && a[child+1] > a[child ])//如果這裡右孩子存在,
//且更大,那麼預設較大的孩子就改為右孩子
{
child++;
}
if(a[child]>a[parent])
{
Swap(&a[child], &a[parent]);
parent = child;
child = parent * 2 + 1;
}
else
{
break;
}
}
}②建堆(將給定的任意陣列建成大堆)
建堆思想:
從倒數第一個非葉子節點開始,從後往前,依次將其作為父親,依次向下調整,一直調整到根的位置
建堆圖示:
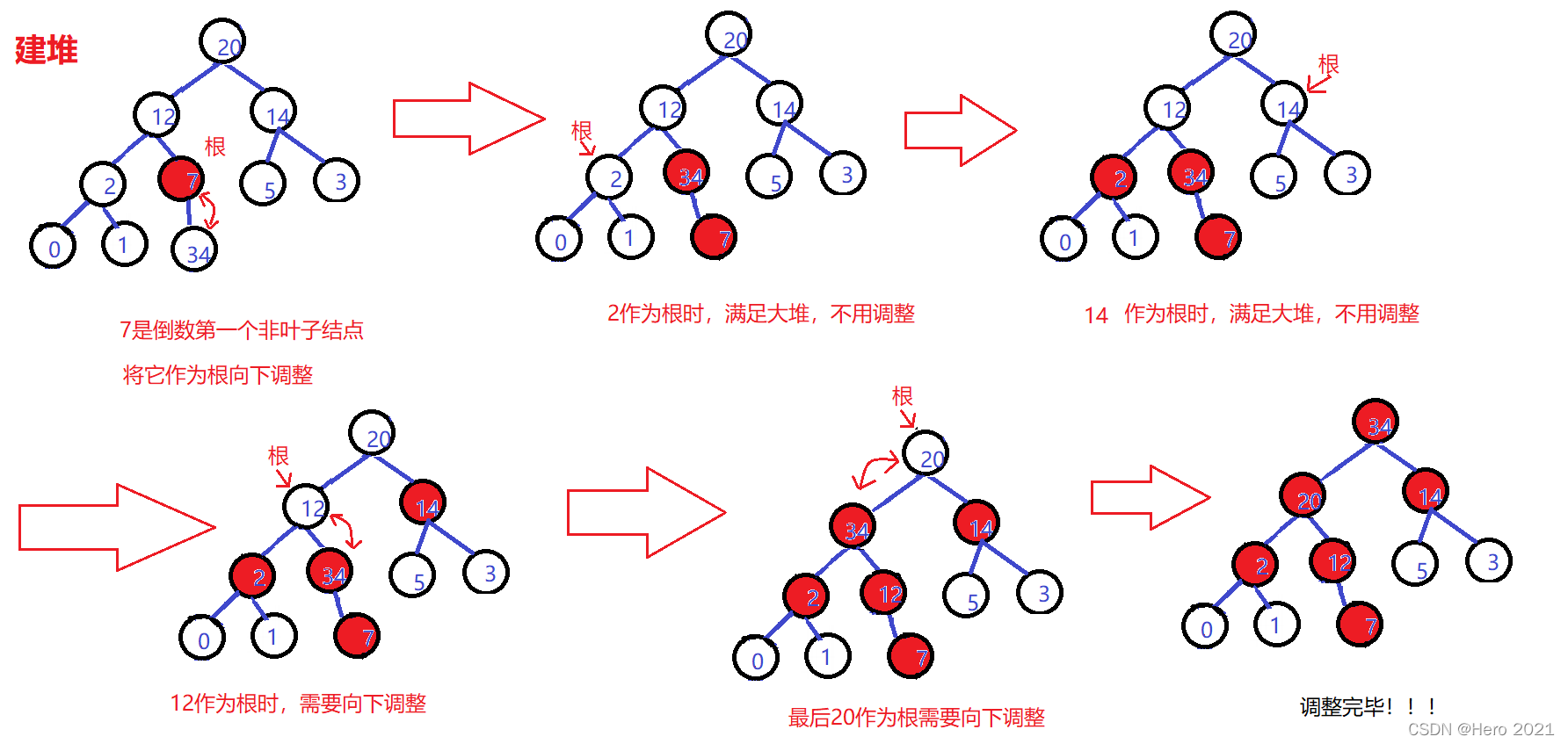
//最後一個葉子結點的父親為i,從後往前,依次向下調整,直到調到根的位置
for (int i = (n - 1 - 1) / 2;i>=0;--i)
{
AdJustDown(a,n,i);
}③堆排序(利用堆刪的思想進行)
堆排序的思想:
1、建好堆之後,將堆頂的數位與最後一個數位交換
2、將最後一個數位不看,剩下的n-1個數位再向下調整成堆再進行第1步3、直到最後只剩一個數停止,這樣就排成有序的了
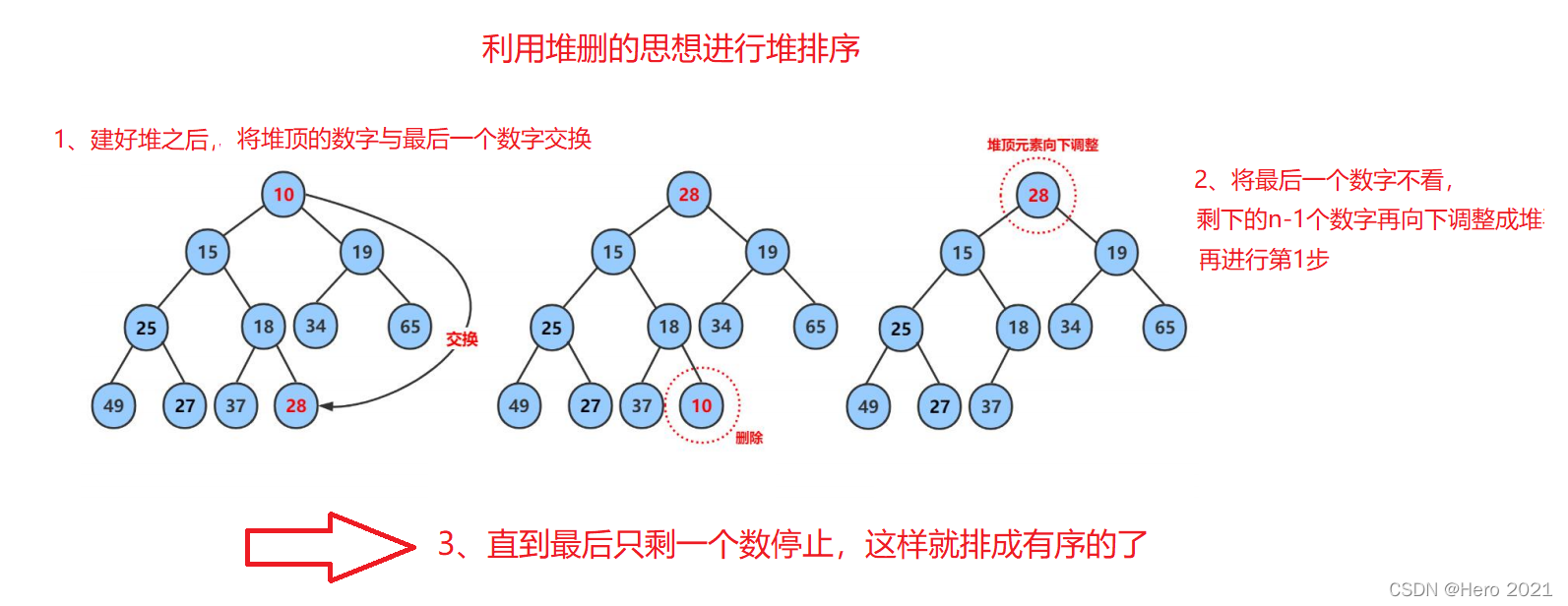
for (int end = n - 1; end > 0; --end)
{
Swap(&a[end],&a[0]);
AdJustDown(a,end,0);
}整體程式碼如下:
void AdJustDown(int* a, int n, int parent)
{
int child = parent * 2 + 1;
while (child < n)
{
if (child + 1 < n && a[child+1] > a[child ])
{
child++;
}
if(a[child]>a[parent])
{
Swap(&a[child], &a[parent]);
parent = child;
child = parent * 2 + 1;
}
else
{
break;
}
}
}
//堆排序
void HeapSort(int*a,int n)
{
for (int i = (n - 1 - 1) / 2;i>=0;--i)
{
AdJustDown(a,n,i);
}
for (int end = n - 1; end > 0; --end)
{
Swap(&a[end],&a[0]);
AdJustDown(a,end,0);
}
}五、氣泡排序
氣泡排序的基本思想:
一趟過程中,前後兩個數依次比較,將較大的數位往後推,下一次只需要比較剩下的n-1個數,如此往復
//優化版本的氣泡排序
void BubbleSort(int* a, int n)
{
int end = n-1;
while (end>0)
{
int exchange = 0;
for (int i = 0; i < end; i++)
{
if (a[i] > a[i + 1])
{
Swap(&a[i], &a[i + 1]);
exchange = 1;
}
}
if (exchange == 0)//單趟過程中,若沒有交換過,證明已經有序,沒有必要再排序
{
break;
}
end--;
}
}氣泡排序總結:
①非常容易理解的排序
②時間複雜度:O(N^2)
③空間複雜度:O(1)
六、快速排序
遞迴版本
1、hoare版本
hoare的單趟思想:
1、左邊作key,右邊先走找到比key小的值
2、左邊後走找到大於key的值
3、然後交換left和right的值
4、一直迴圈重複上述1 2 3步
5、兩者相遇時的位置,與最左邊選定的key值交換
這樣就讓key到達了正確的位置上
動圖演示: 
//hoare版本
//單趟排序 讓key到正確的位置上 keyi表示key的下標,並不是該位置的值
int partion1(int* a, int left, int right)
{
int keyi = left;//左邊作keyi
while (left < right)
{ //右邊先走,找小於keyi的值
while (left < right && a[right] >= a[keyi])
{
right--;
}
//左邊後走,找大於keyi的值
while (left < right && a[left] <= a[keyi])
{
left++;
}
Swap(&a[left], &a[right]);
}
Swap(&a[left], &a[keyi]);
return left;
}
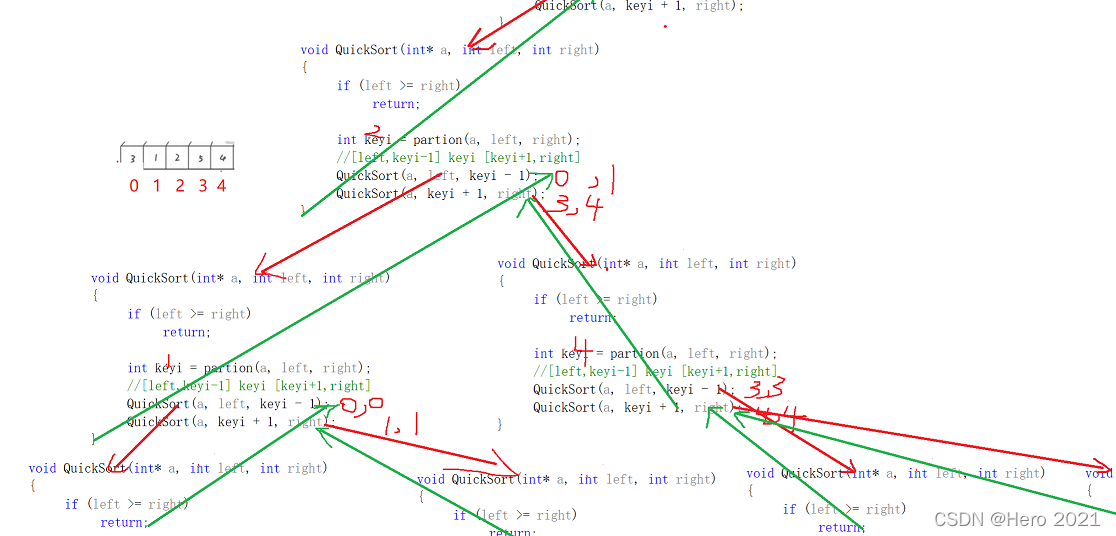
void QuickSort(int* a, int left, int right)
{
if (left >= right)
return;
int keyi = partion1(a, left, right);
//[left,keyi-1] keyi [keyi+1,right]
QuickSort(a, left, keyi - 1);
QuickSort(a, keyi + 1, right);
}2、挖坑法
其實本質上是hoare的變形
挖坑法單趟思想:
1、先將最左邊第一個資料存放在臨時變數key中,形成一個坑位
2、右邊先出發找到小於key的值,然後將該值丟到坑中去,此時形成一個新坑位
3、左邊後出發找到大於key的值,將該值丟入坑中去,此時又形成一個新的坑位
4、一直迴圈重複1 2 3步
5、直到兩邊相遇時,形成一個新的坑,最後將key值丟進去
這樣key就到達了正確的位置上了
動圖演示:

//挖坑法
int partion2(int* a, int left, int right)
{
int key = a[left];
int pit = left;
while (left < right)
{
while (left < right && a[right] >= key)
{
right--;
}
a[pit] = a[right];//填坑
pit=right;
while (left < right && a[left] <= key)
{
left++;
}
a[pit] = a[left];//填坑
pit=left;
}
a[pit] = key;
return pit;
}
void QuickSort(int* a, int left, int right)
{
if (left >= right)
return;
int keyi = partion2(a, left, right);
//[left,keyi-1] keyi [keyi+1,right]
QuickSort(a, left, keyi - 1);
QuickSort(a, keyi + 1, right);
}3、前後指標法(推薦這種寫法)
前後指標的思想:
1、初始時選定prev為序列的開始,cur指標指向prev的後一個位置,同樣選擇最左邊的第一個數位作為key
2、cur先走,找到小於key的值,找到就停下來
3、++prev
4、交換prev和cur為下標的值
5、一直迴圈重複2 3 4步,停下來後,最後交換key和prev為下標的值
這樣key同樣到達了正確的位置
動圖演示:

int partion3(int* a, int left, int right)
{
int prev = left;
int cur = left + 1;
int keyi = left;
while (cur <= right)
{
if (a[cur] < a[keyi] && ++prev != cur)//prev != cur 防止cur和prev相等時,相當於自己和自己交換,可以省略
{ //前置 ++ 的優先順序大於 != 不等於的優先順序
Swap(&a[prev], &a[cur]);
}
++cur;
}
Swap(&a[keyi], &a[prev]);
return prev;
}
void QuickSort(int* a, int left, int right)
{
if (left >= right)
return;
int keyi = partion3(a, left, right);
//[left,keyi-1] keyi [keyi+1,right]
QuickSort(a, left, keyi - 1);
QuickSort(a, keyi + 1, right);
}遞迴展開圖
快速排序的優化
1、三數取中法
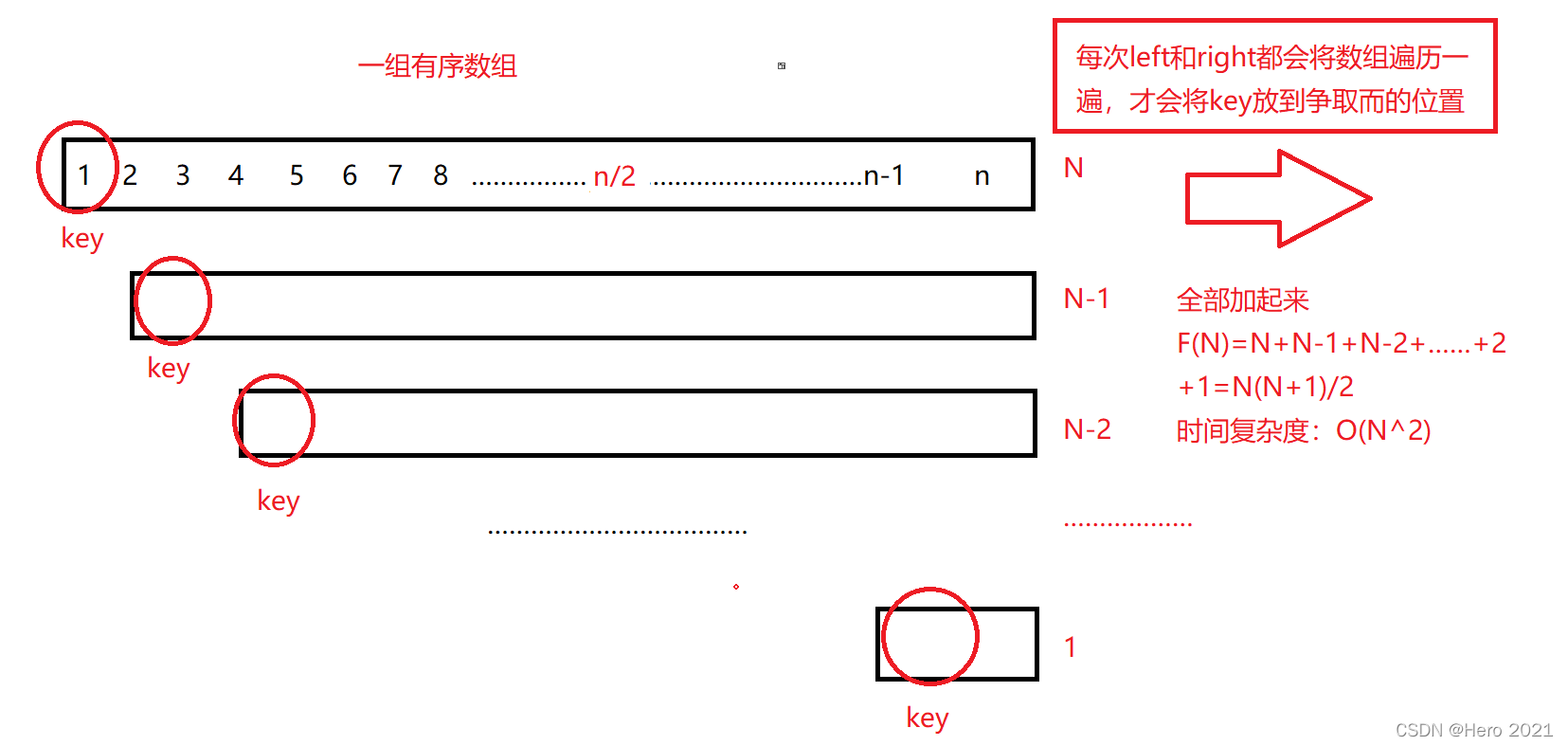
快速排序對於資料是敏感的,如果這個序列是非常無序,雜亂無章的,那麼快速排序的效率是非常高的,可是如果數列有序,時間複雜度就會從O(N*logN)變為O(N^2),相當於氣泡排序了
若每趟排序所選的key都正好是該序列的中間值,即單趟排序結束後key位於序列正中間,那麼快速排序的時間複雜度就是O(NlogN)
但是這是理想情況,當我們面對一組極端情況下的序列,就是有序的陣列,選擇左邊作為key值的話,那麼就會退化為O(N^2)的複雜度,所以此時我們選擇首位置,尾位置,中間位置的數分別作為三數,選出中間位置的數,放到最左邊,這樣選key還是從左邊開始,這樣優化後,全部都變成了理想情況
//快排的優化
//三數取中法
int GetMidIndex(int* a, int left, int right)
{
int mid = (left + right) / 2;
if (a[left] < a[right])
{
if (a[mid] < a[right])
{
return mid;
}
else if (a[mid] > a[right])
{
return right;
}
else
{
return left;
}
}
else
{
if (a[mid] > a[left])
{
return left;
}
else if (a[mid] < a[right])
{
return right;
}
else
{
return mid;
}
}
}
int partion5(int* a, int left, int right)
{
//三數取中,面對有序時是最壞的情況O(N^2),現在每次選的key都是中間值,變成最好的情況了
int midi = GetMidIndex(a, left, right);
Swap(&a[midi], &a[left]);//這樣還是最左邊作為key
int prev = left;
int cur = left + 1;
int keyi = left;
while (cur <= right)
{
if (a[cur] < a[keyi] && ++prev != cur)//prev != cur 防止cur和prev相等時,相當於自己和自己交換,可以省略
{ //前置 ++ 的優先順序大於 != 不等於的優先順序
//++prev;
Swap(&a[prev], &a[cur]);
}
++cur;
}
Swap(&a[keyi], &a[prev]);
return prev;
}2、遞迴到小子區間
隨著遞迴深度的增加,遞迴次數以每層2倍的速度增加,這對效率有著很大的影響,當待排序序列的長度分割到一定大小後,繼續分割的效率比插入排序要差,此時可以使用插排而不是快排
我們可以當劃分割區間長度小於10的時候,用插入排序對剩下的數進行排序
//小區間優化法,可以採用直接插入排序
void QuickSort(int* a, int left, int right)
{
if (left >= right)
return;
if (right - left + 1 < 10)
{
InsertSort(a + left, right - left + 1);
}
else
{
int keyi = partion5(a, left, right);
//[left,keyi-1] keyi [keyi+1,right]
QuickSort(a, left, keyi - 1);
QuickSort(a, keyi + 1, right);
}
}非遞迴版本
遞迴的演演算法主要是在劃分子區間,如果要非遞迴實現快排,只要使用一個棧來儲存區間就可以了。一般將遞迴程式改成非遞迴首先想到的就是使用棧,因為遞迴本身就是一個壓棧的過程。
非遞迴的基本思想:
1. 申請一個棧,存放排序陣列的起始位置和終點位置。
2. 將整個陣列的起始位置和終點位置入棧。
3. 由於棧的特性是:後進先出,right後進棧,所以right先出棧。
定義一個end接收棧頂元素,出棧操作、定義一個begin接收棧頂元素,出棧操作。
4. 對陣列進行一次單趟排序,返回key關鍵值的下標。
5. 這時候需要排基準值key左邊的序列。
如果只將基準值key左邊序列的起始位置和終點位置存入棧中,等左邊排序完將找不到後邊的區間。所以先將右邊序列的起始位置和終點位置存入棧中,再將左邊的起始位置和終點位置後存入棧中。
6.判斷棧是否為空,若不為空 重複4、5步、若為空則排序完成。
void QuickSortNonR(int* a, int left, int right)
{
Stack st;
StackInit(&st);
StackPush(&st,left);
StackPush(&st, right);
while (!StackEmpty(&st))
{
int end = StackTop(&st);
StackPop(&st);
int begin = StackTop(&st);
StackPop(&st);
int keyi = partion5(a,begin,end);
//區間被成兩部分了 [begin,keyi-1] keyi [keyi+1,end]
if (keyi + 1 < end)
{
StackPush(&st,keyi+1);
StackPush(&st,end);
}
if (keyi-1>begin)
{
StackPush(&st, begin);
StackPush(&st, keyi -1);
}
}
StackDestroy(&st);
}快速排序的總結:
①快排的整體綜合效能和使用場景都是比較好的,所以才敢叫快速排序
②快排唯一死穴,就是排一些有序或者接近有序的序列,例如 2,3,2,3,2,3,2,3這樣的序列時,會變成O(N^2)的時間複雜度
③時間複雜度O(N*logN)
④空間複雜度O(logN)
七、歸併排序
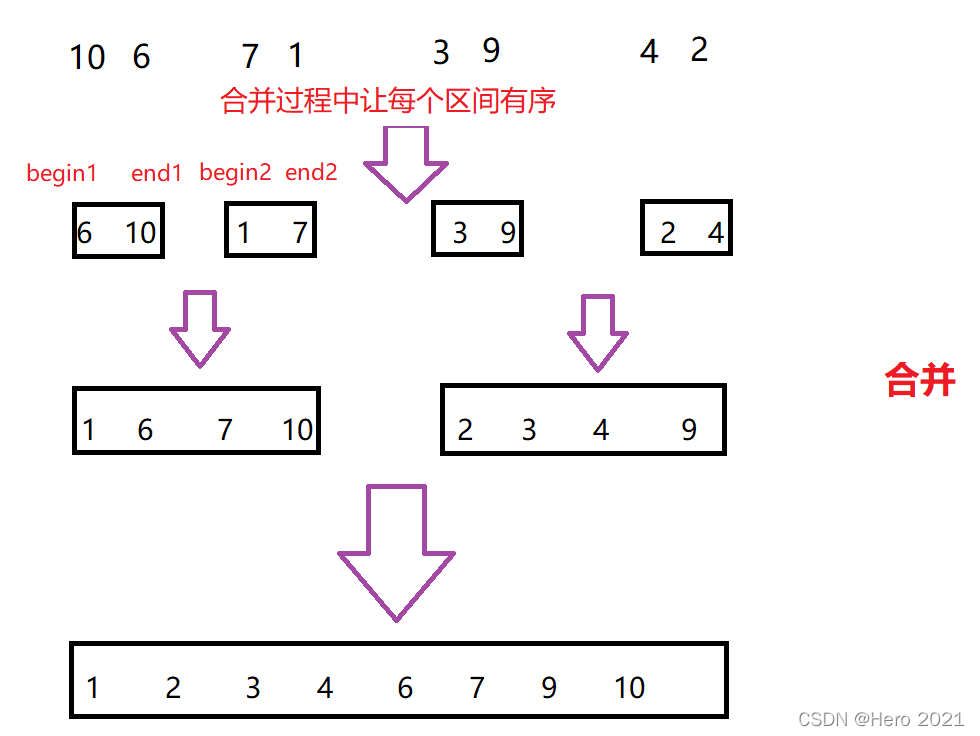
歸併排序的基本思想(分治思想):
1、(拆分)將一段陣列分為左序列和右序列,讓他們兩個分別有序,再將左序列細分為左序列和右序列,如此重複該步驟,直到細分到區間不存在或者只有一個數位為止
2、(合併)將第一步得到的數位合併成有序區間
具體實現:
①拆分
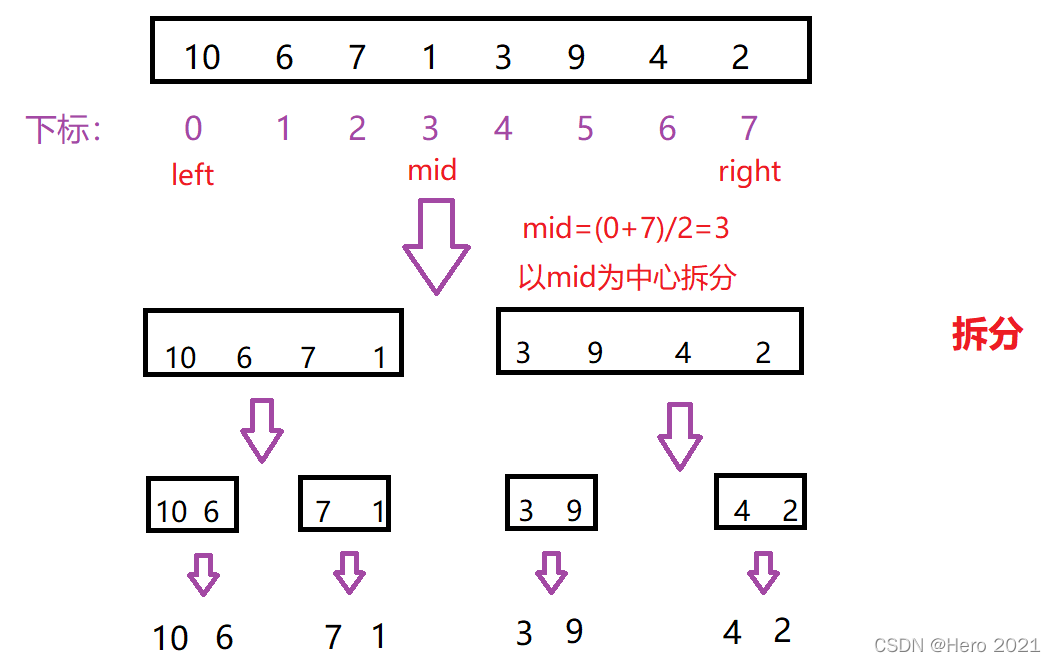
②合併
遞迴實現:
從思想上來說和二元樹很相似,所以我們可以用遞迴的方法來實現歸併排序
程式碼如下:
void _MergeSort(int* a, int left, int right, int* tmp)
{
if (left >= right)
{
return;
}
int mid = (left + right) / 2;
_MergeSort(a, left, mid, tmp);
_MergeSort(a, mid+1, right, tmp);
int begin1 = left, end1 = mid;
int begin2 = mid + 1, end2 = right;
int i = left;
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] < a[begin2])
{
tmp[i++] = a[begin1++];
}
else
{
tmp[i++] = a[begin2++];
}
}
while (begin1 <= end1)
{
tmp[i++] = a[begin1++];
}
while (begin2 <= end2)
{
tmp[i++] = a[begin2++];
}
for (int j = left; j <= right; j++)
{
a[j] = tmp[j];
}
}
//歸併排序
void MergeSort(int* a, int n)
{
int* tmp = (int*)malloc(sizeof(int)*n);
if (tmp == NULL)
{
printf("malloc fail\n");
exit(-1);
}
_MergeSort(a,0,n-1,tmp);
free(tmp);
tmp = NULL;
}非遞迴實現:
我們知道,遞迴實現的缺點就是會一直呼叫棧,而棧記憶體往往是很小的。所以,我們嘗試著用迴圈的辦法去實現
由於我們操縱的是陣列的下標,所以我們需要藉助陣列,來幫我們儲存上面遞迴得到的陣列下標,和遞迴的區別就是,遞迴要將區間一直細分,要將左區間一直遞迴劃分完了,再遞迴劃分右區間,而藉助陣列的非遞迴是一次性就將資料處理完畢,並且每次都將下標拷貝回原陣列
歸併排序的基本思路是將待排序序列a[0…n-1]看成是n個長度為1的有序序列,將相鄰的有序表成對歸併,得到n/2個長度為2的有序表;將這些有序序列再次歸併,得到n/4個長度為4的有序序列;如此反覆進行下去,最後得到一個長度為n的有序序列。
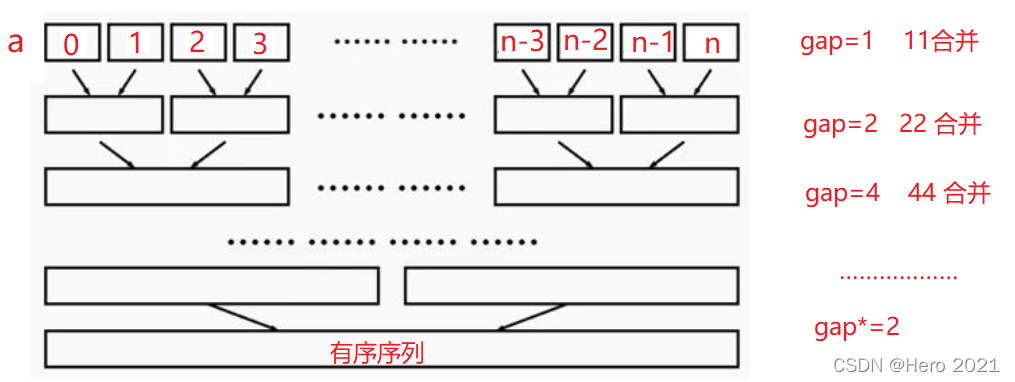
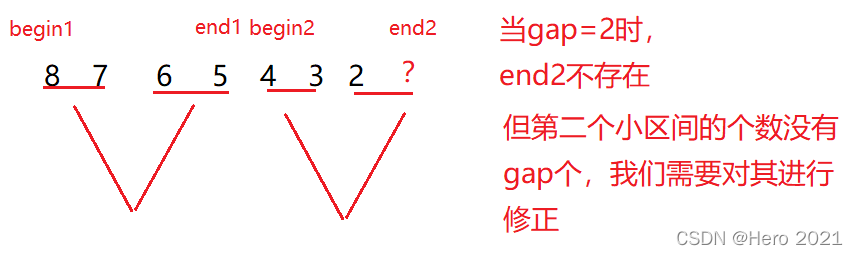
但是我們這是理想情況下(偶數個),還有特殊的邊界控制,當資料個數不是偶數個時,我們所分的gap組,勢必會有越界的地方
第一種情況:
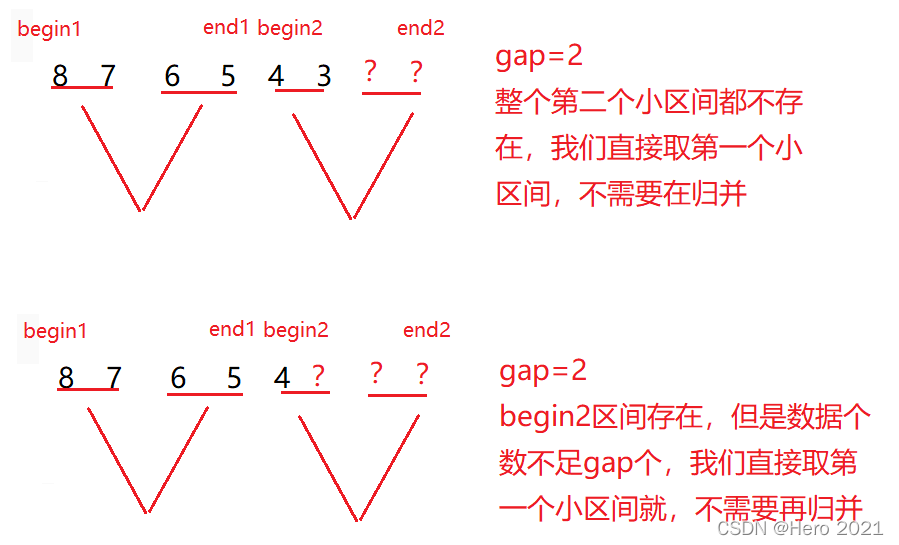
第二種情況:
程式碼如下:
void MergeSortNonR(int* a, int n)
{
int* tmp = (int*)malloc(sizeof(int)*n);
if (tmp == NULL)
{
printf("malloc fail\n");
exit(-1);
}
int gap = 1;
while (gap < n)
{
for (int i = 0; i < n; i += 2 * gap)
{
// [i,i+gap-1] [i+gap,i+2*gap-1]
int begin1 = i, end1 = i + gap - 1;
int begin2 = i + gap, end2 = i + 2 * gap - 1;
// 核心思想:end1、begin2、end2都有可能越界
// end1越界 或者 begin2 越界都不需要歸併
if (end1 >= n || begin2 >= n)
{
break;
}
// end2 越界,需要歸併,修正end2
if (end2 >= n)
{
end2 = n- 1;
}
int index = i;
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] < a[begin2])
{
tmp[index++] = a[begin1++];
}
else
{
tmp[index++] = a[begin2++];
}
}
while (begin1 <= end1)
{
tmp[index++] = a[begin1++];
}
while (begin2 <= end2)
{
tmp[index++] = a[begin2++];
}
// 把歸併小區間拷貝回原陣列
for (int j = i; j <= end2; ++j)
{
a[j] = tmp[j];
}
}
gap *= 2;
}
free(tmp);
tmp = NULL;
}
歸併排序的總結:
①缺點是需要O(N)的空間複雜度,歸併排序更多的是解決磁碟外排序的問題
②時間複雜度:O(N*logN)
③空間複雜度:O(N)
八、計數排序
又叫非比較排序,又稱為鴿巢原理,是對雜湊直接定址法的變形應用
基本思想:
1、統計相同元素出現的個數
2、根據統計的結果,將資料拷貝回原陣列
具體實現:
①統計相同元素出現的個數
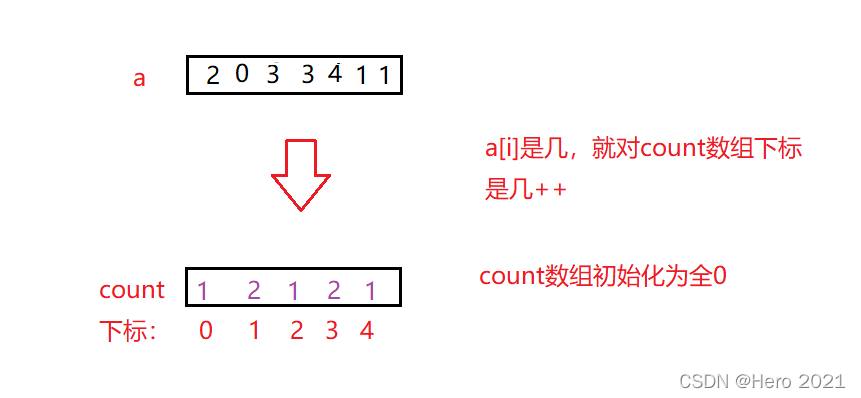
對於給定的任意陣列a,我們需要開闢一個計數陣列count,a[i]是幾,就對count陣列下標是幾++
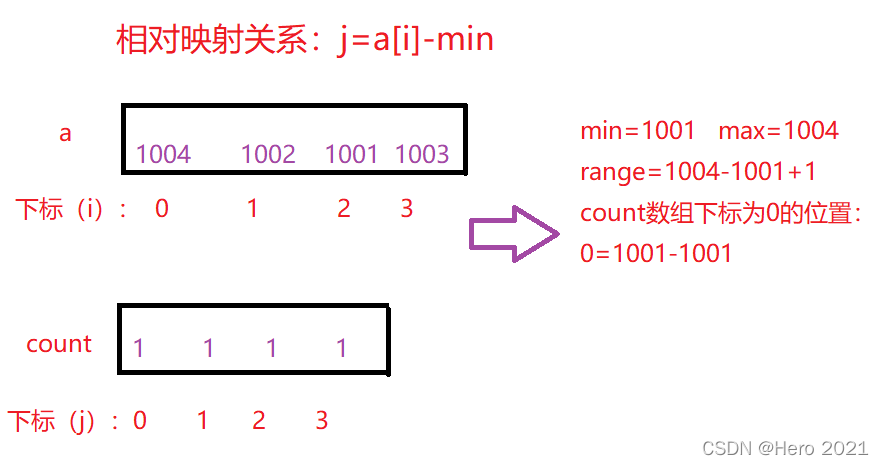
這裡我們用到了絕對對映,即a[i]中的陣列元素是幾,我們就在count陣列下標是幾的位置++,但是對於資料比較聚集,不是從較小的數位開始,例如1001,1002,1003,1004這樣的資料,我們就可以用到相對對映的方法,以免開闢陣列空間的浪費,count陣列的空間大小我們可以用a陣列中最大值減去最小值+1來確定(即:range=max-min+1),我們可以得到count陣列下標 j =a[i]-min
②根據count陣列的結果,將資料拷貝回a陣列
count[j]中資料是幾,說明該數出現了幾次,是0就不用拷貝

程式碼如下:
void CountSort(int* a, int n)
{
int min = a[0], max = a[0];//如果不賦值,min和max就是預設隨機值,最好給賦值一個a[0]
for (int i=1;i<n;i++)//修正 找出A陣列中的最大值和最小值
{
if (a[i] < min)
{
min=a[i];
}
if (a[i]>max)
{
max=a[i];
}
}
int range = max - min + 1;//控制新開陣列的大小,以免空間浪費
int* count = (int*)malloc(sizeof(int) * range);
memset(count,0, sizeof(int) * range);//初始化為全0
if (count==NULL)
{
printf("malloc fail\n");
exit(-1);
}
//1、統計資料個數
for (int i=0;i<n;i++)
{
count[a[i]-min]++;
}
//2、拷貝回A陣列
int j = 0;
for (int i=0;i<range;i++)
{
while (count[i]--)
{
a[j++] = i + min;
}
}
free(count);
count = NULL;
}計數排序總結:
①在資料範圍比較集中時,效率很高,但是使用場景很有限,可以排負數,但對於浮點數無能為力
②時間複雜度:O(MAX(N,range))
③空間複雜度:O(range)
八大排序的穩定性總結:
穩定的排序有:直接插入排序、氣泡排序、歸併排序
不穩定的排序有:希爾排序、選擇排序、堆排序、快速排序、計數排序