選擇排序

我們熟知的選擇排序，其採用的就是貪心策略。
它所採用的貪心策略即為每次從未排序的資料中選取最小值，並把最小值放在未排序資料的起始位置，直到未排序的資料為0，則結束排序。

void swap(int* arr, int i, int j)
{
	int tmp = arr[i];
	arr[i] = arr[j];
	arr[j] = tmp;
}

void selectSort(int* arr, int n)
{
	//降序
	for (int i = 0; i < n; i++)
	{
		int maxIndex = i;
		for (int j = i+1; j < n; j++)
		{
			if (arr[j] >= arr[maxIndex])
				maxIndex = j;
		}
		swap(arr, i, maxIndex);
	}
}

平衡字串

問題描述：

在一個 平衡字串 中，‘L’ 和 ‘R’ 字元的數量是相同的。
給你一個平衡字串 s，請你將它分割成儘可能多的平衡字串。
注意：分割得到的每個字串都必須是平衡字串，且分割得到的平衡字串是原平衡字串的連續子串。
返回可以通過分割得到的平衡字串的 最大數量 。

貪心策略：從左往右掃描，只要達到平衡，就立即分割，不要有巢狀的平衡。
故可以定義一個變數balance，在遇到不同的字元時，向不同的方向變化，當balance為0時達到平衡，分割數更新。
比如：從左往右掃描字串s，遇到L，balance-1，遇到R，balance+1.當balance為0時，更新cnt++
如果最終cnt==0，說明s只需要保持原樣，返回1

程式碼實現：

class Solution {
public:
    int balancedStringSplit(string s) {
        if(s.size() == 1)
            return 0;
        int cnt = 0;
        int balance = 0;
        for(int i = 0; i < s.size(); i++)
        {
            if(s[i] == 'R')
                --balance;
            else 
                ++balance;
            if(balance == 0)
                cnt++;
        }
        if(cnt == 0)
            return 1;

        return cnt;
    }
};

買股票的最佳時機

問題描述：

給定一個陣列 prices ，其中 prices[i] 是一支給定股票第 i 天的價格。
設計一個演演算法來計算你所能獲取的最大利潤。你可以儘可能地完成更多的交易（多次買賣一支股票）。
注意：你不能同時參與多筆交易（你必須在再次購買前出售掉之前的股票）。

貪心策略：
連續上漲交易日：第一天買最後一天賣收益最大，等價於每天都買賣。
連續下降交易日：不買賣收益最大，即不會虧錢。
故可以遍歷整個股票交易日價格列表，在所有上漲交易日都買賣（賺到所有利潤），所有下降交易日都不買賣（永不虧錢）

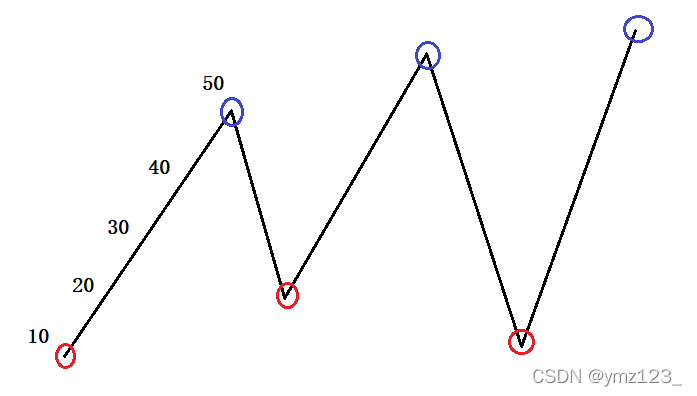
例如從10到50是連續上漲的5天，可以第一天買入，最後一天賣出，利潤為40，等價於第一天買入第二天賣出，第二天再買入。。。以此類推

程式碼實現：

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        int profit = 0;
        for(int i = 0; i < prices.size() - 1; i++)
        {
            if(prices[i] <= prices[i+1])
                profit += prices[i+1] - prices[i];
        }

        return profit;
    }
};

跳躍遊戲

問題描述：

給定一個非負整數陣列 nums ，你最初位於陣列的 第一個下標 。
陣列中的每個元素代表你在該位置可以跳躍的最大長度。
判斷你是否能夠到達最後一個下標。

貪心策略：
根據題目描述，對於陣列中的任意一個位置y，只要存在一個位置x，它本身可以到達，並且它跳躍的最大長度為x+nums[x]，這個值大於等於y，即x+nums[x] >= y，那麼位置y也可以到達。即對於每一個可以到達的位置x，它使得x+1，x+2，…，x+nums[x] >= y，那麼位置y也可以到達。
一次遍歷陣列中的每一個位置，並實時更新最遠可以到達的位置。對於當前遍歷到的位置x，如果它在最遠可以到達的位置範圍內，那麼我們就可以從起點通過若干次跳躍達到該位置，因此我們可以用x+nums[x]更新最遠可以到達的位置。
在遍歷的過程中，如果最遠可以到達的位置大於等於陣列中的最後一個位置，那就說明最後一個位置可到達，直接返回true。遍歷結束後，最後一個位置仍不可達，返回false。
例如：[2, 3, 1, 1, 4]
一開始在位置0，可跳躍的最大長度為2，因此最遠可以到達的位置倍更新為2；繼續遍歷到位置1，由於1<=2，因此位置1可達。用1加上它最大可跳躍的長度3，將最遠可以到達的位置更新為4，4大於最後一個位置4，返回true

程式碼實現：

class Solution {
public:
    bool canJump(vector<int>& nums) {
        int maxLen = nums[0];
        for(int i = 0; i < nums.size(); i++)
        {
            if(i <= maxLen)
            {
                maxLen = max(i + nums[i],maxLen);
                if(maxLen >= nums.size() - 1)
                    return true;
            }
        }

        return false;
    }
};

錢幣找零

問題描述：

假設1元、2元、5元、10元、20元、50元、100元的紙幣分別有c0, c1, c2, c3, c4, c5, c6張。現在要用這些錢來支付K元，至少要用多少張紙幣？

貪心策略：
顯然，每一步儘可能用面值大的紙幣即可。在日常生活中我們也是這麼做的。

程式碼實現：

//按面值降序
struct cmp {
	bool operator()(vector<int>& a1, vector<int>& a2) {
		return a1[0] > a2[0];
	}
};

int solve(vector<vector<int>>& moneyCount, int money)
{
	int num = 0;
	sort(moneyCount.begin(), moneyCount.end(), cmp());
	//首先選擇最大面值的紙幣
	for (int i = 0; i < moneyCount.size() - 1; i++)
	{
		//選擇需要的當前面值和該面值有的數量中的較小值
		int c = min(money / moneyCount[i][0], moneyCount[i][1]);
		money -= c * moneyCount[i][0];
		num += c;
	}
	if (money > 0)
		num = -1;
	return num;
}

多機排程問題

問題描述：

某工廠有n個獨立的作業，由m臺相同的機器進行加工處理。作業i所需的加工時間為ti，任何作業在被處理時不能中斷，也不能進行拆分處理。現廠長請你給他寫一個程式：算出n個作業由m臺機器加工處理的最短時間。
輸入：第一行T（1<T<100)表示有T組測試資料。每組測試資料的第一行分別是整數n，m（1<=n<=10000，1<=m<=100），接下來的一行是n個整數ti（1<=t<=100)。
輸出：所需的最短時間

貪心策略：
這個問題還沒有最優解，但是用貪心選擇策略可設計出較好的近似演演算法（求次優解）
當n<=m時，只要將作業分給每一個機器即可；當n>m時，首先將n個作業時間從大到小排序，然後依此順序將作業分配給下一個作業馬上結束的處理機。也就是說從剩下的作業中選擇需要處理時間最長的，然後依次選擇處理時間次長的，直到所有作業全部處理完畢，或者機器不能再處理其他作業為止。如果我們每次是將需要處理時間最短的作業分配給空閒的機器，那麼可能就會儲秀安其它所有作業都處理完了只剩下所需時間最長的作業在處理的情況，這樣勢必效率較低。

程式碼實現：

struct cmp{
	bool operator()(const int& x, const int& y){
		return x > y;
	}
};

int findMax(vector<int>& machines)
{
	int ret = 0;
	for (int i = 0; i < machines.size(); i++)
	{
		if (machines[i] > machines[ret])
			ret = i;
	}

	return machines[ret];
}

int greedStrategy(vector<int>& works, vector<int>& machines)
{
	//降序
	sort(works.begin(), works.end(), cmp());
	int n = works.size();
	int m = machines.size();
	for (int i = 0; i < n; i++)
	{
		int finish = 0;
		int machineTime = machines[finish];
		for (int j = 1; j < m; j++)
		{
			if (machines[j] < machines[finish])
			{
				finish = j;
			}
		}
		machines[finish] += works[i];
	}

	return findMax(machines);
}

活動選擇

問題描述：

有n個需要在同一天使用同一個教室的活動a1, a2, …, an，教室同一時刻只能由一個活動使用。每個活動a[i]都有一個開始時間s[i]和結束時間f[i]。一旦被選擇後，活動a[i]就佔據半開時間區間[s[i],f[i])。如果[s[i],f[i])和[s[j],f[j])互不重疊，a[i]和a[j]兩個活動就可以被安排在這一天。求使得儘量多的活動能不衝突的舉行的最大數量。

貪心策略：
1.每次都選擇開始時間最早的活動，不能得到最優解。
2.每次都選擇持續時間最短的活動，不能得到最優解。

3.每次選取結束時間最早的活動（結束時間最早意味著開始時間也早），可以得到最優解。按這種方法選擇，可以為未安排的活動留下儘可能多的時間。如下圖的活動集合S，其中各項活動按照結束時間單調遞增排序。

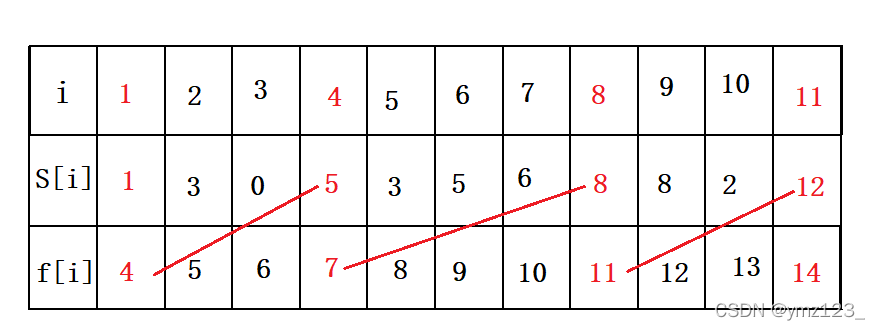
程式碼實現：

struct cmp{
	bool operator()(vector<int>& s1, vector<int>& s2){
		return s1[1] < s2[1];
	}
};

int getMaxNum(vector<vector<int>>& events)
{
	sort(events.begin(), events.end(), cmp());
	int num = 1;
	int i = 0;
	for (int j = 1; j < events.size();j++)
	{
		if (events[j][0] >= events[i][1])
		{
			++num;
			i = j;
		}
	}

	return num;
}

無重疊區間

問題描述：

給定一個區間的集合，找到需要移除區間的最小數量，使剩餘區間互不重疊。
注意:
可以認為區間的終點總是大於它的起點。
區間 [1,2] 和 [2,3] 的邊界相互「接觸」，但沒有相互重疊。

貪心策略：
法一：與上題活動選擇類似，用總區間數減去最大可同時進行的區間數即為結果。
法二：
當按照起點先後順序考慮區間時，利用一個prev指標追蹤剛剛新增到最終列表中的區間。遍歷時，可能遇到三種情況：
情況1：當前考慮的兩個區間不重疊。這種情況下不移除任何區間，將prev賦值為後面的區間，移除區間數量不變。

情況2：兩個區間重疊，後一個區間的終點在前一個區間的終點之前。由於後一個區間的長度更小，可以留下更多空間，容納更多區間，將prev更新為當前區間，移除區間的數量+1

情況3：兩個區間重疊，後一個區間的終點在前一個區間的終點之後。直接移除後一個區間，留下更多空間。因此，prev不變，移除區間的數量+1

程式碼實現：
法一：

struct cmp{
	bool operator()(vector<int>& s1, vector<int>& s2){
		return s1[1] < s2[1];
	}
};

class Solution {
public:
    int eraseOverlapIntervals(vector<vector<int>>& intervals) {
        sort(intervals.begin(), intervals.end(), cmp());
        int num = 1;
        int i = 0;
        for(int j = 1; j < intervals.size(); j++)
        {
            if(intervals[j][0] >= intervals[i][1])
            {
                i = j;
                num++;
            }
        }

        return intervals.size() - num;
    }
};

法二：

struct cmp{
	bool operator()(vector<int>& s1, vector<int>& s2){
		return s1[1] < s2[1];
	}
};

class Solution {
public:
    int eraseOverlapIntervals(vector<vector<int>>& intervals) {
        if(intervals.empty())
            return 0;
        sort(intervals.begin(), intervals.end(), cmp());
        int prev = 0;
        int num = 0;
        for(int i = 1; i < intervals.size(); i++)
        {
            //情況1 不衝突
            if(intervals[i][0] >= intervals[prev][1])
            {
                prev = i;
            }
            else
            {
                if(intervals[i][1] < intervals[prev][1])
                {
                    //情況2
                    prev = i;
                }
                num++;
            }
        }

        return num;
    }
};